Элементы теории корреляции. Линейная корреляция. Лекция 18

1.

Лекция 18
Элементы теории корреляции.
Линейная корреляция.
Аскарова А.Ж.

2. План лекции

1. Корреляционная зависимость.
2. Коэффициент корреляции.
3. Свойства коэффициента
корреляции.
Аскарова А.Ж.

3. Корреляционная зависимость

Во многих задачах требуется установить или
оценить зависимость изучаемо случайной величины
Y от одной или нескольких других случайных
величин.
Две случайные величины могут быть связаны:
- функциональной зависимостью
- статистической
- независимой
Строгая функциональная зависимость
реализуется редко, т.к. обе случайных величины или
одна подвержены действию других случайных
величин.
Аскарова А.Ж.

4. Корреляционная зависимость

Статистической называется зависимость, при
которой изменение одной из величин влечет
изменение распределения другой.
В частности она проявляется в том что
изменение одной из величин влечет изменение
среднего значения другой. Такая статистическая
зависимость называется корреляционной.
Аскарова А.Ж.

5. Корреляционная зависимость

Предположим изучается связь между случайными
величинами Х и Y. Пусть каждому значению Х
соответствует несколько значений Y.
Условным средним YХ называется среднее
арифметическое случайной величины Y соответствующее
значению случайной величины Х равное х.
Если каждому значению Х соответствует одно значение
YХ , то очевидно что она – функция от х.
В этом случае говорят, что случайная величина Y
зависит от Х корреляционно.

6. Корреляционная зависимость

Корреляционной зависимостью Yx называют
функциональную зависимость YХ от значений х.
YХ = f(x) - уравнение регрессии Y на Х, а график –
линией регрессии Y на Х. f(x) – функция регрессии.
Аналогично определяется условная средняя Х на Y:
Х Y = f(y).

7. Метод корреляции

Метод корреляции применяется для того, чтобы при
сложном
взаимодействии
посторонних
влияний
выяснить, какова была бы зависимость между
результатом и фактором, если бы посторонние
причины
(факторы)
не
изменялись
и
своим
изменением не искажали основную зависимость.

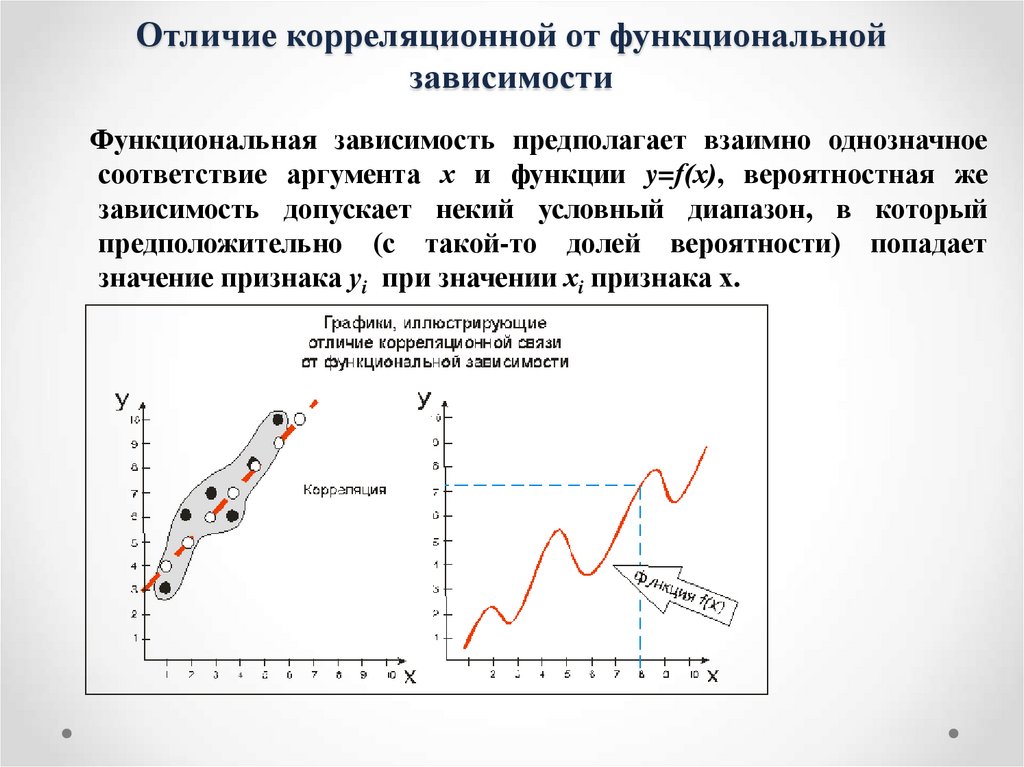
8. Отличие корреляционной от функциональной зависимости

Функциональная зависимость предполагает взаимно однозначное
соответствие аргумента х и функции y=f(х), вероятностная же
зависимость допускает некий условный диапазон, в который
предположительно (с такой-то долей вероятности) попадает
значение признака уi при значении хi признака х.

9. Задачи корреляции

Первая задача корреляции:
Если связь существует, то нужно установить ее форму – вид
функциональной зависимости между
и величиной Х:
выявление на основе наблюдений над большим количеством
фактов того, как изменяется в среднем результативный
признак в связи с изменением данного фактора (парная
корреляция)
или
группы
факторов
(множественная
корреляция). Эта задача решается нахождением уравнения
связи.
Вторая задача корреляции:
Оценить тесноту (силу) корреляционной связи: определение
степени влияния искажающих факторов. Эта задача решается
при помощи различных показателей тесноты связи:
коэффициента корреляции, корреляционного отношения.

10.

Коэффициент корреляции
Коэффициент корреляции используется для
оценки тесноты связи между величинами при
прямолинейной зависимости.
Обозначается буквой r и определяется по формуле:
x x y y
n
r
i 1
i
i
x x y y
n
i 1
2
i
n
i 1
i
2
, где

11.

Коэффициент корреляции
x -среднее
значение
(причинного) признака
x
x
факториального
i
n
y -среднее значение результативного признака
y
y
n
i

12.

Коэффициент корреляции
Промежуточные вычисления удобно располагать в виде
таблицы:
№
наблю
дения
xi yi x i x xi x yi y y y x x y y
i
i
i
… …
…
…
2
…
2
…
…

13.

Свойства коэффициента корреляции
Величина коэффициента корреляции находится в
пределах 1 r 1 :
1) Чем ближе |r| к 1, тем теснее связь между
факториальным и результативным признаками.
2) при |r|=1 получается полная функциональная
связь.
3) если |r| →0 , то связь между признаками слабая.

14.

Свойства коэффициента корреляции
4) при |r|=0 связи между признаками нет
(линейная зависимость отсутствует).
5) при r>0 зависимость между признаками
прямая (возрастающая).
6) при r<0 зависимость обратная (убывающая).
Если зависимость между признаками прямая, то
можно
пользоваться
уравнением
прямой
регрессии:
у у by / x x x
, где

15.

Свойства коэффициента корреляции
by/x - коэффициент
определяется по формуле:
регрессии,
x x y y
n
by / x
i 1
i
i
x x
n
i 1
i
2
который

16.

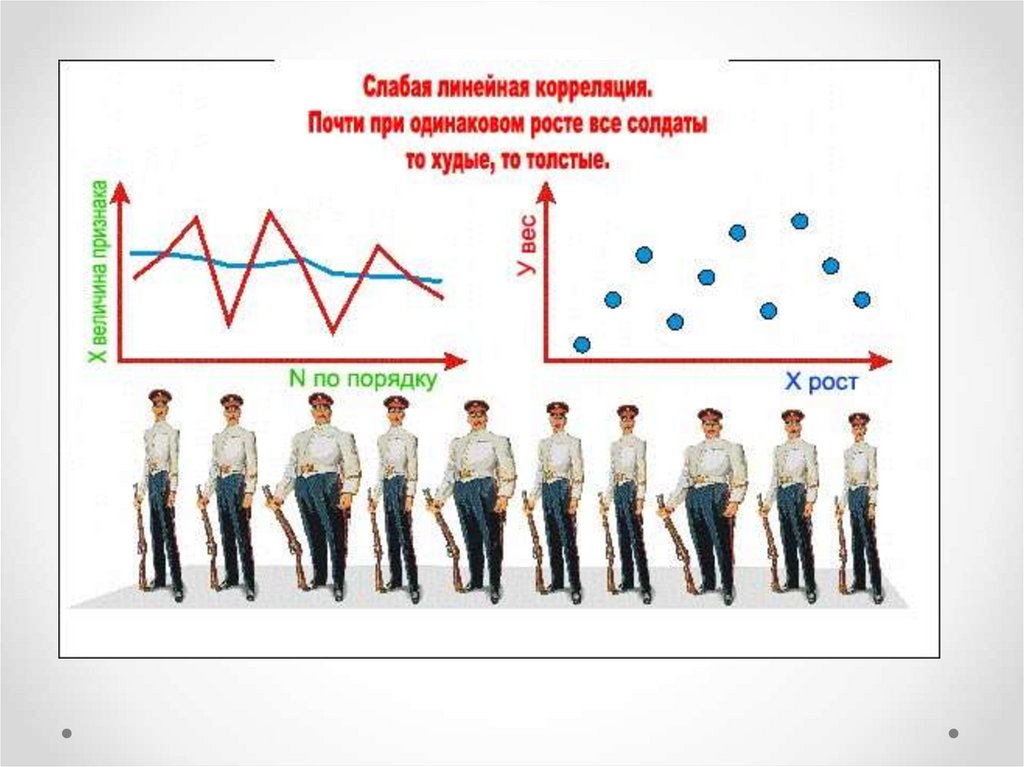
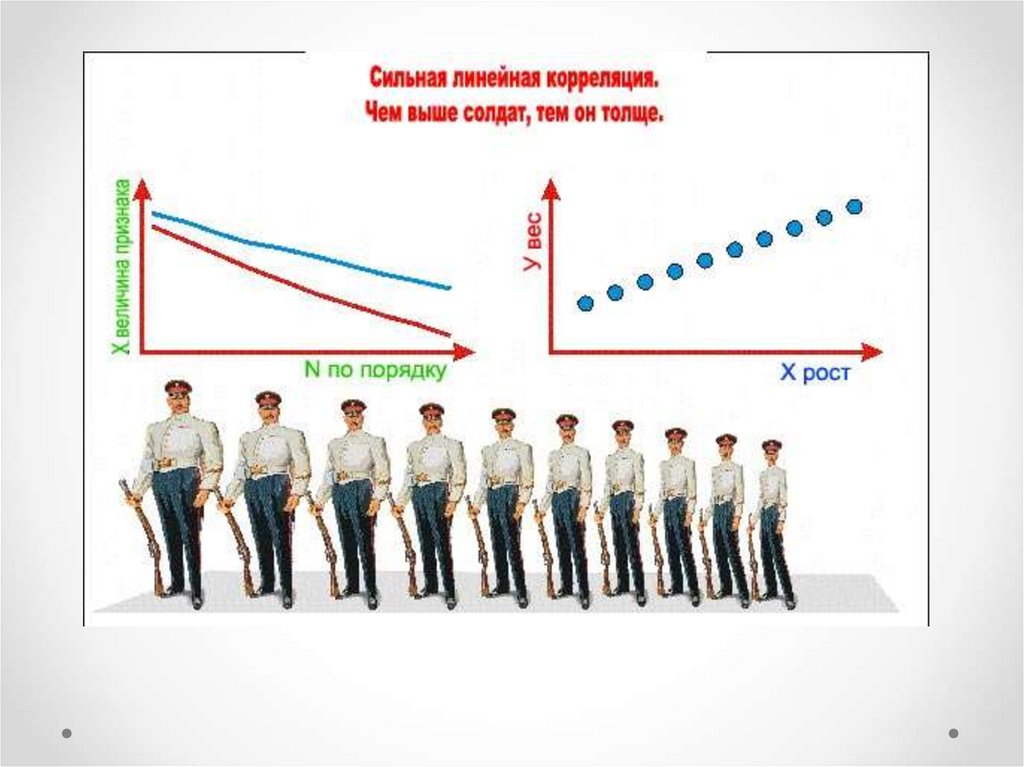
Свойства коэффициента корреляции
Если точки не выстраиваются по прямой линии, а образуют
«облако», коэффициент корреляции по абсолютной величине
становится меньше единицы и по мере округления этого
облака приближается к нулю.
Положительная
корреляция
Отрицательная
корреляция
Отсутствие
корреляционной
зависимости

17.

Свойства коэффициента корреляции

18. Примеры корреляционной зависимости

19.

Свойства коэффициента корреляции
Значение коэффициента корреляции
(Value of r)
0,8 r 1
0,8 r 1
Сила линейной взаимосвязи
(STRENGHT
OF
RELATIONSHIP )
Сильная взаимосвязь, близкая к
функциональной (strong)
0,6 r 0,8
0,6 r 0,8
Взаимосвязь средней силы
(moderate)
0,40< r ≤ 0,6
Умеренная
0,20< r
Слабая взаимосвязь (weak)
≤ 0,4
0 r 0,2
LINEAR
очень слабая взаимосвязь

20. Проверка значимости коэффициента корреляции Пирсона

Нулевая и альтернативная гипотезы имеют вид:
Н0: коэффициент корреляции Пирсона r незначимый;
Н1: коэффициент корреляции Пирсона r значим.
• Рассчитывается t-статистика по формуле:
t расч .
r
1 r2
( n 2)
• Определяется tтабл по таблице Стьюдента со степенями
свободы n-2 и уровнем значимости α
• Если t расч t табл , то Н0 отклоняют на заданном уровне
значимости, и считаем, что коэффициент корреляции
Пирсона значимый.

21.

22.

23.

24.

ПРИМЕР
Для 10 петушков 15 дневного возраста были
получены следующие данные о весе их тела (х) в
граммах и весе гребня (у) (в мг):
xi
83
72
69
90
90
95
91
75
70
yi
56
42
18
84
56 107 90
68
31
48
95

25.

ПРИМЕР
Требуется:
1) найти коэффициент корреляции и сделать вывод
о
тесноте
и
направлении
линейной
корреляционной связи между признаками;
2) составить уравнение прямой регрессии;
3) нанести на чертеж исходные данные и построить
прямую регрессии.
Решение:
Составим вспомогательную таблицу

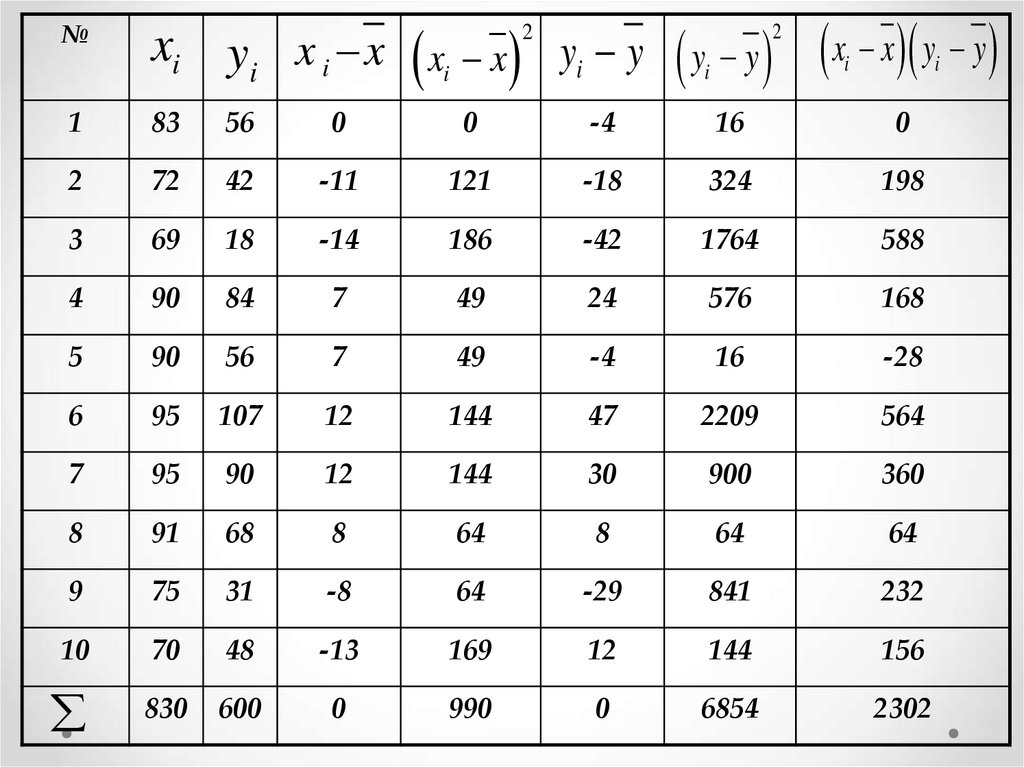
26.

№
xi yi x i x xi x 2 yi y yi y 2
x x y y
i
i
1
83
56
0
0
-4
16
0
2
72
42
-11
121
-18
324
198
3
69
18
-14
186
-42
1764
588
4
90
84
7
49
24
576
168
5
90
56
7
49
-4
16
-28
6
95
107
12
144
47
2209
564
7
95
90
12
144
30
900
360
8
91
68
8
64
8
64
64
9
75
31
-8
64
-29
841
232
10
70
48
-13
169
12
144
156
830
600
0
990
0
6854
2302

27.

Решение
Вычисляем средние:
y
600
x
i
830
i
у
60
x
83
n
10
n
10
1) найдем коэффициент корреляции:
r
x x y y
i
i
x x y y
2
i
i
2
r
2302
990 6854
0,88

28.

Решение
Вывод: между весом тела х и весом гребня у
у 15- дневных петушков существует тесная
положительная линейная корреляционная связь.
2) найдем коэффициент регрессии:
by / x
x x y y
x x
i
i
2
i
2302
by / x
2,32
990
Аскарова А.Ж.

29.

Решение
Подставим в уравнение прямой регрессии:
y y by / x x x
y 60 2, 32 x 83
y 2, 32 x 132, 56
Аскарова А.Ж.

30.

Решение
3) наносим исходные данные на координатную
плоскость и строим найденную прямую
регрессии.
у
100
М2
60
у
х
М1
83; 60
М 2 57; 0
20
57
М1
70
90 х
Аскарова А.Ж.

31. Непараметрические показатели корреляции

Определение. Под качественным подразумевается признак, который
невозможно измерить точно, но он позволяет сравнить объекты между
собой и расположить их в порядке убывания или возрастания
качества.
Под ранжированием будем понимать упорядочивание объектов
согласно убыванию качественного признака
Для оценки степени связи качественных признаков используют
коэффициенты ранговой корреляции.
Коэффициент корреляции Спирмена — мера линейной связи между
случайными величинами. Корреляция Спирмена является
ранговой, то есть для оценки силы связи используются не
численные значения, а соответствующие им ранги.
Коэффициент корреляции Кендалла — мера линейной связи между
случайными величинами

32. Непараметрические показатели корреляции

Чарльз Э́двард Спи́рмен (1863-1945)
Профессор Лондонского и
Честерфилдского университетов.
Разработчик многочисленных
методик математической
статистики. Создатель двухфакторной
теории интеллекта и техники
факторного анализа.
Мо́рис Джордж Ке́ндалл (1907-1983)
английский статистик.
автор многочисленных трудов
по статистике и теории вероятностей.

33. Схема нахождения коэффициента Корреляции Спирмена

1. Определить, какие два признака или две иерархии
признаков будут участвовать в сопоставлении как
переменные X и Y.
2. Проранжировать значения переменной X, присваивая
ранг 1 наименьшему значению, и т.д. Занести ранги в
первый столбец таблицы по порядку номеров
испытуемых или признаков.
3. Проранжировать значения переменной У, в соответствии
с теми же правилами. Занести ранги во второй столбец
таблицы по порядку номеров испытуемых или признаков.
4. Подсчитать разности d между рангами X и Y по каждой
строке таблицы и занести в третий столбец таблицы.

34. Схема нахождения коэффициента Корреляции Спирмена

Возвести каждую разность в квадрат: d2. Эти значения
занести в четвертый столбец таблицы.
6. Подсчитать сумму d2.
7. При наличии одинаковых рангов рассчитать поправки:
где a - объем каждой группы одинаковых рангов в
ранговом ряду X;
b - объем каждой группы одинаковых
рангов в ранговом ряду Y.
5.

35.

Схема нахождения коэффициента Корреляции
Спирмена
Рассчитать коэффициент ранговой корреляции rs по
формуле:
при отсутствии одинаковых рангов
8.
при наличии одинаковых рангов
где sum(d2) - сумма квадратов разностей между рангами;
Ta и Tb - поправки на одинаковые ранги;
N - количество наблюдений признаков, участвовавших в
ранжировании.

36. Проверка значимости коэффициента ранговой корреляции Спирмена

Нулевая и альтернативная гипотезы имеют вид:
Н0: коэффициент ранговой корреляции Спирмена rs незначимый;
Н1: коэффициент ранговой корреляции Спирмена rs значим.
• Рассчитывается t-статистика по формуле:
t расч.
rs
1 rs2
(n 2)
• Определяется tтабл по таблице Стьюдента со степенями
свободы n-2 и уровнем значимости α
• Если t расч t табл , то Н0 отклоняют на заданном уровне
значимости, и считаем, что коэффициент ранговой корреляции
Спирмена значимый.

37.

https://www.youtube.com/watch?v=GtlGWqlr
Mww
Расчет коэффициента корреляции в Excel
https://www.youtube.com/watch?v=wQxaf3L
UJcg
Основы корреляционного анализа
Аскарова А.Ж.