Similar presentations:
Статистические критерии различий (1)
1. Статистические критерии различий
2. Основания классификации:
• 1. По типу измерительной шкалы.• 2. По максимальному объему
выборок.
• 3. По количеству выборок, которые
можно сравнивать.
• 4. По характеру выборок (зависимые
или независимые).
3. Параметрические критерии
• Основаны на конкретном типераспределения генеральной
совокупности (нормальном) или
использует параметры этой
совокупности (средние, дисперсии и
т.д.).
4. Непараметрические критерии
• Не базируются на предположении отипе распределения генеральной
совокупности и не используют
параметры этой совокупности.
5.
Параметрическиекритерии
Позволяют прямо оценить
различия в средних,
полученных в двух выборках
Непараметрические
критерии
Позволяют оценить лишь
средние тенденции
Значения признака должны
быть измерены в
метрических шкалах
Распределение признака
является нормальным
Математические расчеты
довольно сложны
Значения признака могут
быть представлены в любой
шкале
Распределение признака
может быть любым
Математические расчеты
просты
6.
Параметрическиекритерии
Непараметрические
критерии
t-Стьюдента для
независимых
выборок;
F-Фишера
t-Стьюдента для
зависимых
выборок
U-Манна-Уитни;
Q-Розенбаума
Более двух
независимых
выборок
ANOVA
Н-Краскала-Уоллеса
Более двух
зависимых
выборок
ANOVA с
повторными
измерениями
χ2-Фридмана
(хи-квадрат)
Две
независимые
выборки
Две зависимые
выборки
Т-Вилкоксона;
G-знаков
7. Критерий t-Стьюдента для независимых выборок
• Уильям С. Госсет• 1908 г.
• Опубликовал
результаты исследования
под псевдонимом
Student
8.
• Статистические гипотезы:• H0: M1 = M2
• H1: M1 ≠ M2
• Условия использования:
• выборки являются независимыми;
• распределение в обеих выборках
соответствует нормальному.
9.
• Альтернатива – U-Манна-Уитни, еслираспределение в одной или обеих
выборках отличается от нормального
10.
tMx My
Для равночисленных
выборок
Dx Dy
Nx N y
df N1 N 2 2
t
Mx My
(x M
i
) ( yi M y )
2
x
(n 1) n
df N1 N 2 2
2
11.
XY
(xi-Mx)
(yi-My)
(xi-Mx)2
(yi-My)2
1
2
3
12
10
11
9
12
8
-0,1
-2,1
-1,1
-0,7
2,3
-1,7
0,01
4,41
1,21
0,49
5,29
2,89
4
5
6
14
12
10
12
12
12
1,9
-0,1
-2,1
2,3
2,3
2,3
3,61
0,01
4,41
5,29
5,29
5,29
7
8
9
9
14
14
2
5
11
-3,1
1,9
1,9
-7,7
-4,7
1,3
9,61
3,61
3,61
59,29
22,09
1,69
10
15
14
2,9
4,3
8,41
18,49
Σ
121
97
0
0
38,9
126,1
№
• Mx=121/10=12,1 My=97/10=9,7
12.
t эм п.12,1 9,7
38,9 126,1
(10 1) 10
df 10 10 2
1,7
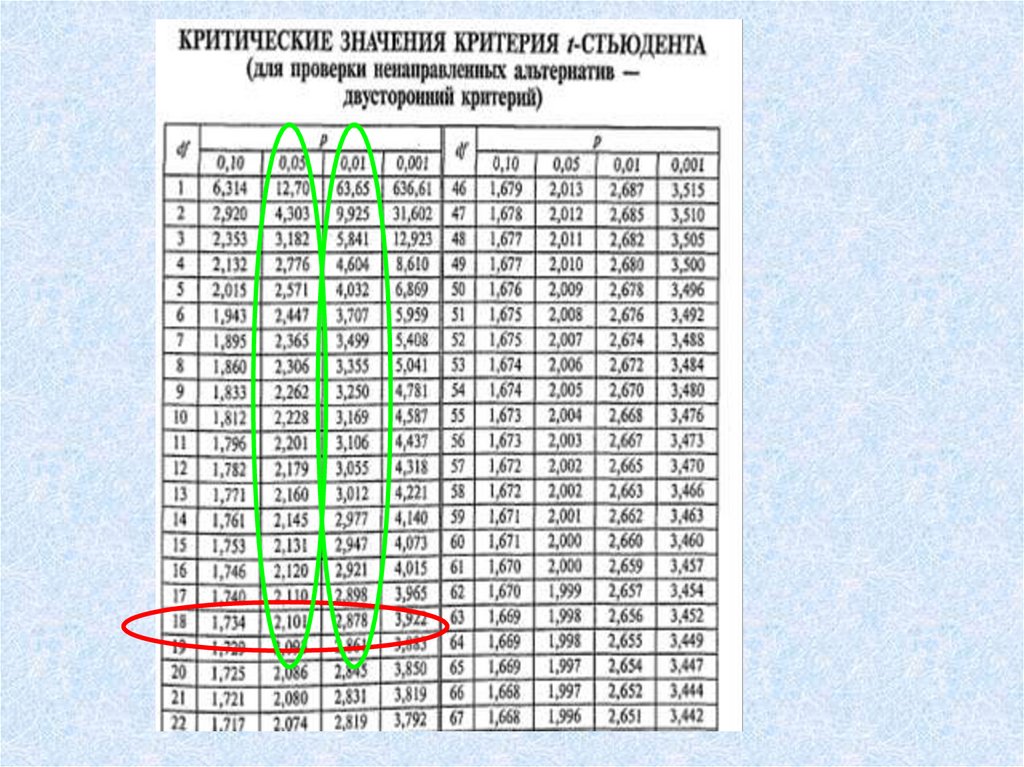
13.
14.
p=0,05p=0,01
зона незначимости
зона значимости
зона неопределенности
1,7
2,101
2,878
Подтверждается гипотеза
H 0.
Не обнаружены
статистически
достоверные различия
между показателями
выборок X и Y.
15. Критерий F-Фишера
• Статистические гипотезы:• H0: D1 = D2
• H1: D1 ≠ D2
• Условия использования:
• выборки являются независимыми;
• распределение в обеих выборках
соответствует нормальному;
• результаты представлены в интервальной или
абсолютной (шкале отношений) шкалах.
16.
df1 n1 1df 2 n2 1
D
F
D
2
x
2
y
Большая
дисперсия
Меньшая
дисперсия
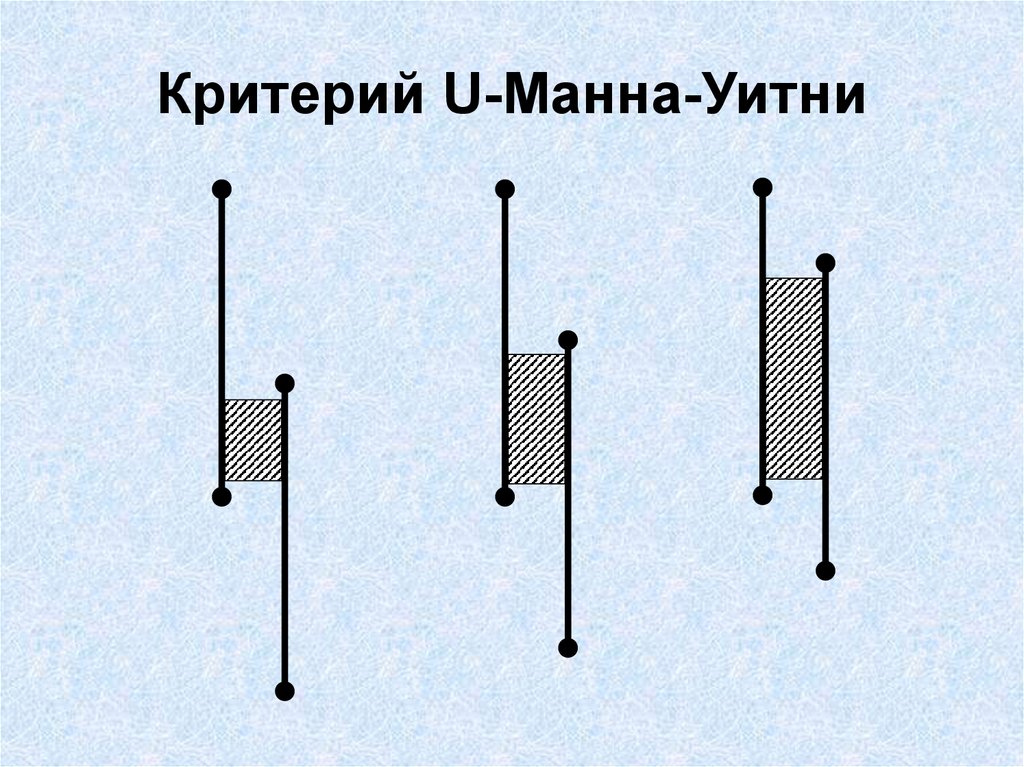
17. Критерий U-Манна-Уитни
18.
Чем меньше эмпирическое значение U, тембольше различия
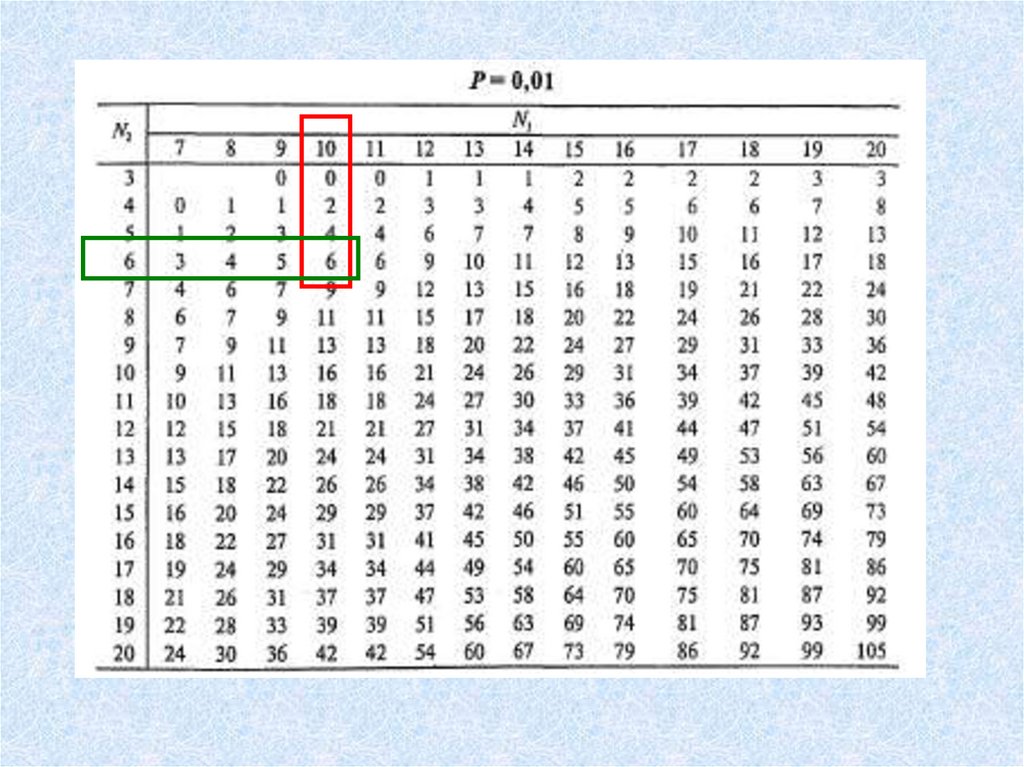
p=0,01
зона значимости
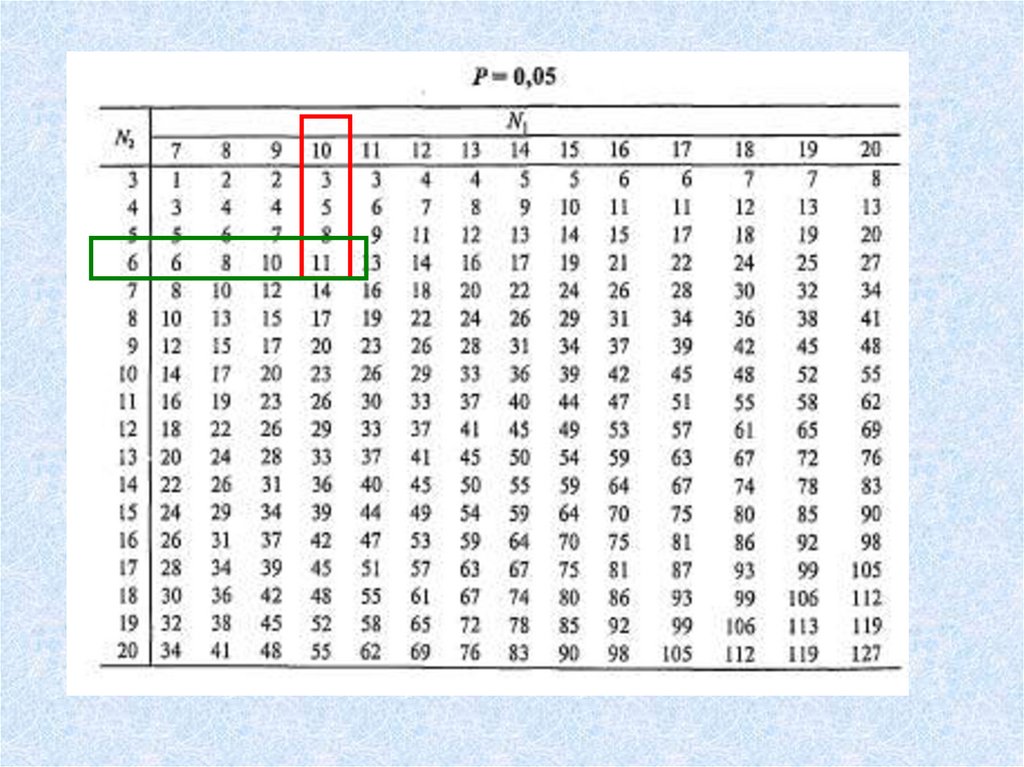
p=0,05
зона неопределенности
зона незначимости
19.
nx (nx 1)U (n1 n2 )
Tx
2
n1 – объем первой выборки
n2 – объем второй выборки
Тх – большая из ранговых сумм
nx – объем группы с большей суммой рангов
20. Ограничения критерия
• 1. В каждой выборке должно быть не менее3 испытуемых.
• 2. Допускается, чтобы в одной выборке
было 2 испытуемых, но тогда во второй
выборке их должно быть не менее 5.
• 3. В каждой выборке должно быть не более
60 испытуемых.
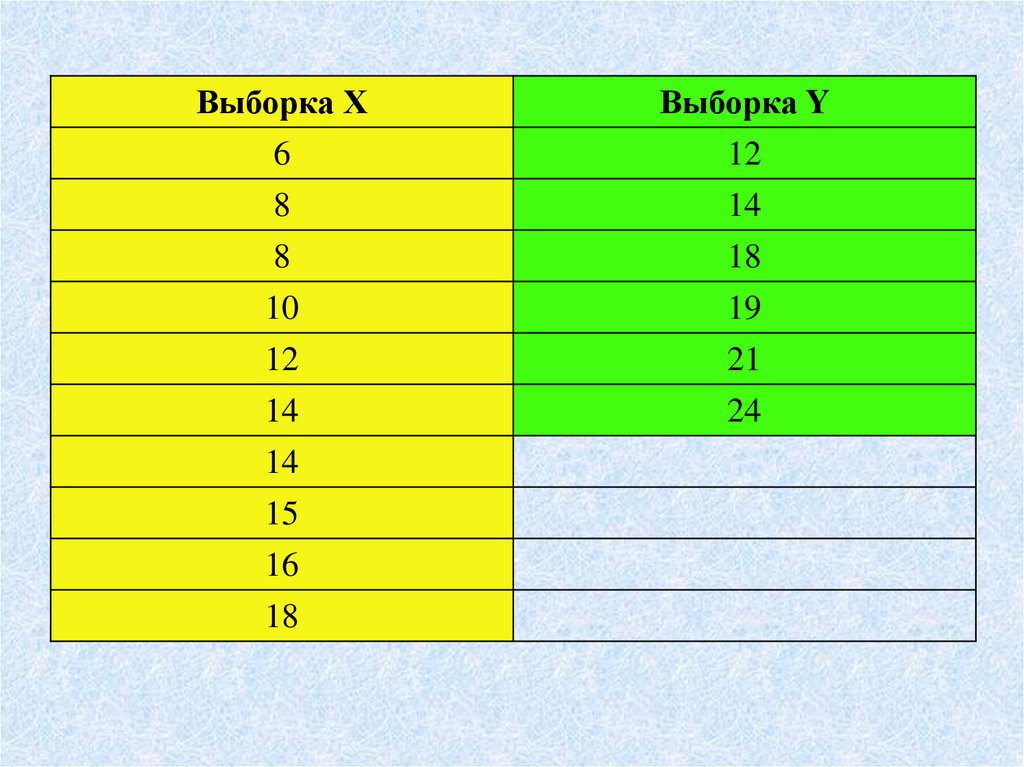
21.
Выборка Х6
8
Выборка Y
12
14
8
10
12
18
19
21
14
14
15
24
16
18
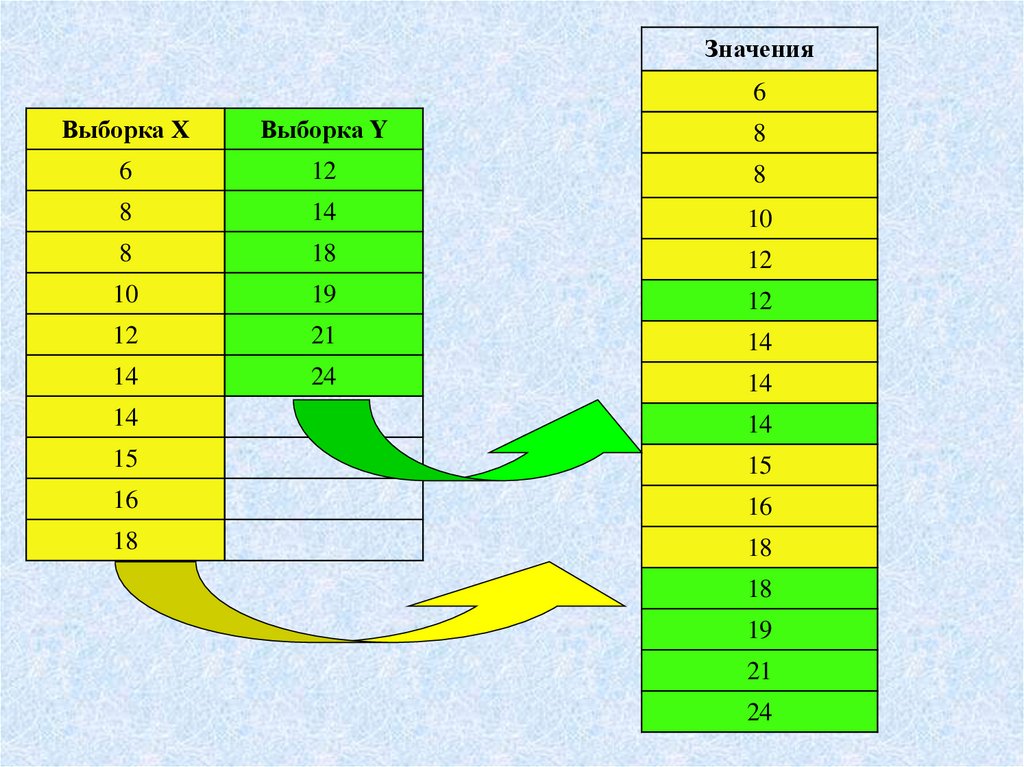
22.
Значения6
Выборка Х
Выборка Y
8
6
12
8
8
14
10
8
18
12
10
19
12
12
21
14
14
24
14
14
14
15
15
16
16
18
18
18
19
21
24
23.
№Значения
Выборка
1
6
X
2
8
X
3
8
X
4
10
X
5
12
X
6
12
Y
7
14
X
8
14
X
9
14
Y
10
15
X
11
16
X
12
18
X
13
18
Y
14
19
Y
15
21
Y
16
24
Y
Ранг
Ранг (X)
Ранг (Y)
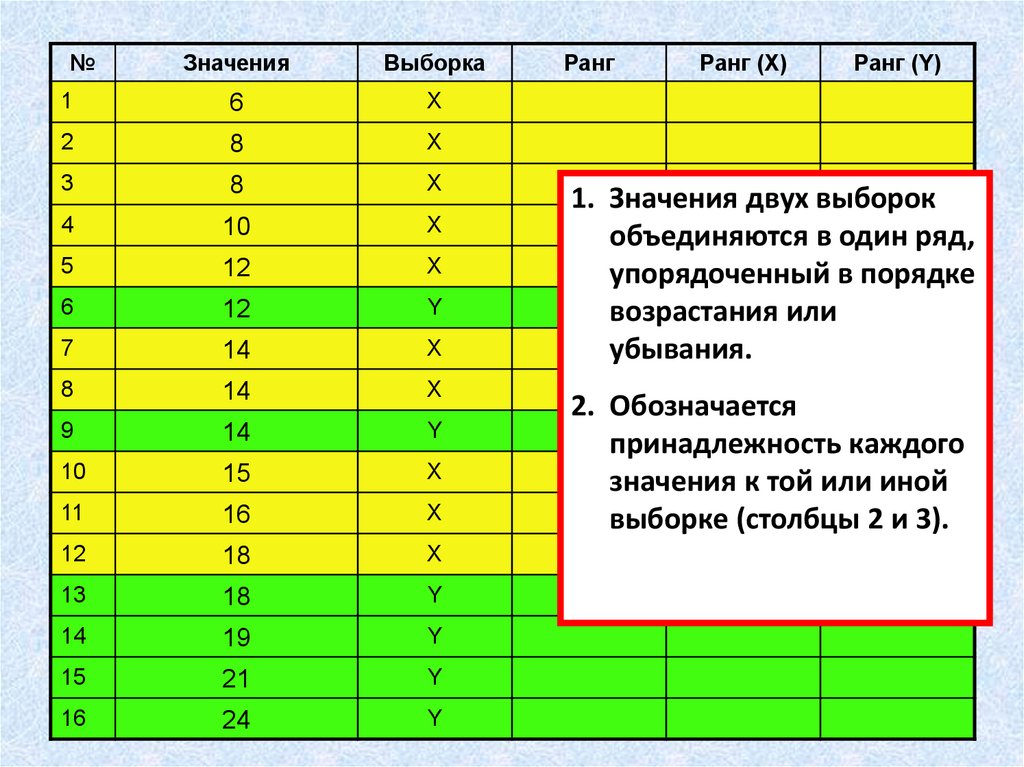
1. Значения двух выборок
объединяются в один ряд,
упорядоченный в порядке
возрастания или
убывания.
2. Обозначается
принадлежность каждого
значения к той или иной
выборке (столбцы 2 и 3).
24.
№Значения
Выборка
Ранг
Ранг (X)
1
6
X
1
1
2
8
X
2,5
2,5
3
8
X
2,5
2,5
4
10
X
4
4
5,5
5,5
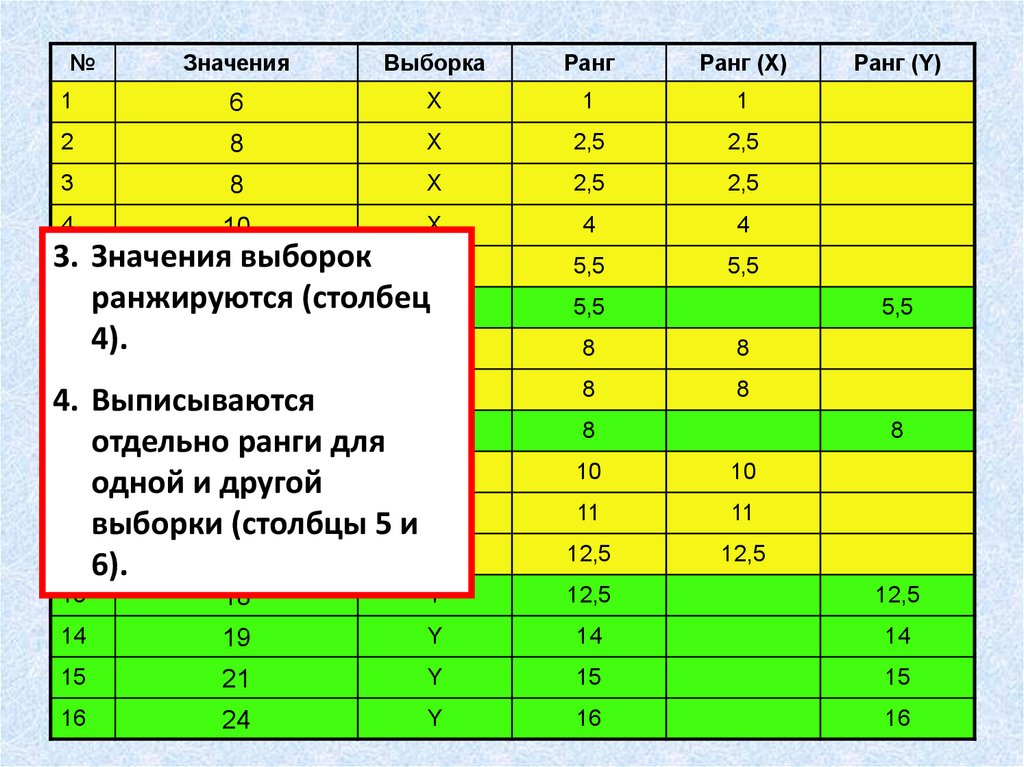
3.
5 Значения12выборок
X
(столбецY
6 ранжируются
12
7 4).
X
14
8
X
14
4.
Выписываются
9
отдельно14ранги для Y
10
X
15
одной и другой
11
выборки16
(столбцы 5 и X
12
X
18
6).
5,5
Ранг (Y)
5,5
8
8
8
8
8
8
10
10
11
11
12,5
12,5
13
18
Y
12,5
12,5
14
19
Y
14
14
15
21
Y
15
15
16
24
Y
16
16
25.
№Значения
Выборка
Ранг
Ранг (X)
1
6
X
1
1
2
8
X
2,5
2,5
3
8
X
2,5
2,5
4
10
X
4
4
5
12
X
5,5
5,5
Y
5,5
X
8
8
X
8
8
Y
8
X
10
10
5. Вычисляются суммы
6
12
рангов по
X и Y.
7
14
6.
8 Значения
14
в
9 подставляются
14
10 формулу15
Ранг (Y)
5,5
8
11
16
X
11
11
12
18
X
12,5
12,5
13
18
Y
12,5
12,5
14
19
Y
14
14
15
21
Y
15
15
16
24
Y
16
16
Сумма рангов
65
71
26.
• U – Манна-Уитни6 (6 1)
U (10 6)
71
2
• U эмп. = 10
7. Определяется уровень значимости и делается
статистический вывод
27.
28.
29. Проверка значимости
p=0,01зона значимости
p=0,05
зона неопределенности
8
10
зона незначимости
14





















 mathematics
mathematics








