Similar presentations:
Рычажные механизмы. Кинематический анализ механизмов
1.
1. Рычажные механизмы1.2. Кинематический анализ механизмов
А. В. Ступин
2.
Оглавление1.2. Кинематический анализ механизмов
1.2.1. Задачи кинематического анализа
1.2.2. Планы скоростей и ускорений
1.2.3. Пример решения задачи о скоростях и ускорениях
1.3. Динамический анализ механизмов
1.3.1. Цели и задачи динамического анализа
1.3.2. Силы, действующие на звенья механизмов
1.3.3. Определение сил инерции подвижных звеньев механизма
1.3.4. Направление реакций в кинематических парах
1.3.5. Определение реакций в кинематических парах
2
3.
1.2.1. Задачикинематического анализа
• Кинематический анализ состоит в определении движения
звеньев механизма по заданному закону движения
ведущих звеньев.
• Основные задачи кинематического анализа:
1) Определение положения звеньев,
а также траекторий отдельных точек звеньев;
2) Определение скоростей и ускорений.
• При решении указанных задач считаются известными:
‒ законы движения ведущих звеньев;
‒ кинематическая схема механизма
с указанием размеров звеньев.
3
4.
1.2.1. Задачикинематического анализа
Задачи о положениях, скоростях и ускорениях решаются
применительно к группам Ассура, которыми образован
механизм:
1) Проводится структурный анализ и классификация
механизма по Ассуру.
2) Выбирается ведущее звено.
Задаётся закон движения этого звена.
4
5.
1.2.1. Задачикинематического анализа
3) Выбирается масштаб чертежа.
На чертеже наносятся неподвижные элементы
кинематических пар механизма.
По заданной обобщенной координате строится
положение ведущего звена.
4) Строятся планы положений каждой группы Ассура
в соответствии с последовательностью образования
ими механизма.
5) Строятся планы скоростей и ускорений
применительно к группам Ассура.
5
6.
1.2.1. Задачикинематического анализа
• Масштабы для планов положений, скоростей и ускорений
выбираются произвольно.
• При анализе рычажных передач
под масштабом той или иной величины принято понимать
отношение этой величины к отрезку, который изображает
ее на чертеже:
‒ масштаб плана положений механизма μl, м/мм;
‒ масштаб плана скоростей μv, м·с-1/мм;
‒ масштаб плана ускорений μa, м·с-2/мм.
6
7.
1.2.1. Задачикинематического анализа
y
3
lCD
z
β
5
4
C
2
E
lDE
α
D
B
1
A
lBD
lBC
φ1
x
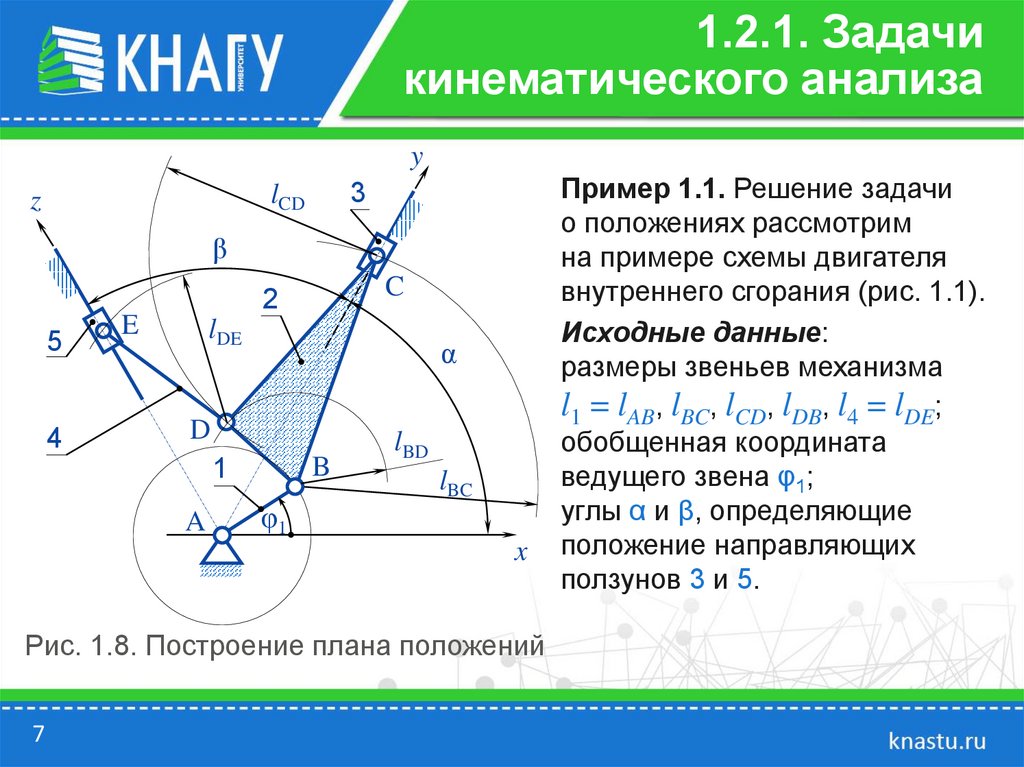
Рис. 1.8. Построение плана положений
7
Пример 1.1. Решение задачи
о положениях рассмотрим
на примере схемы двигателя
внутреннего сгорания (рис. 1.1).
Исходные данные:
размеры звеньев механизма
l1 = lAB, lBC, lCD, lDB, l4 = lDE;
обобщенная координата
ведущего звена φ1;
углы α и β, определяющие
положение направляющих
ползунов 3 и 5.
8.
1.2.1. Задачикинематического анализа
y
3
lCD
z
β
5
4
C
2
E
lDE
α
D
B
1
A
φ1
lBD
lBC
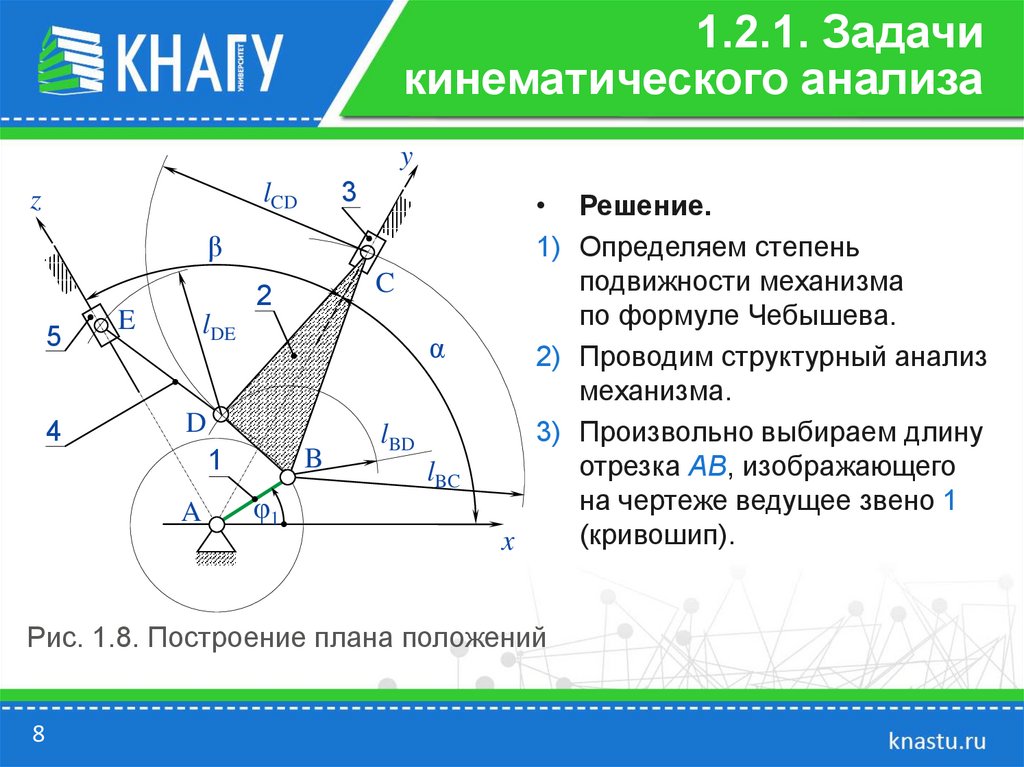
• Решение.
1) Определяем степень
подвижности механизма
по формуле Чебышева.
2) Проводим структурный анализ
механизма.
3) Произвольно выбираем длину
отрезка АВ, изображающего
на чертеже ведущее звено 1
(кривошип).
x
Рис. 1.8. Построение плана положений
8
9.
1.2.1. Задачикинематического анализа
y
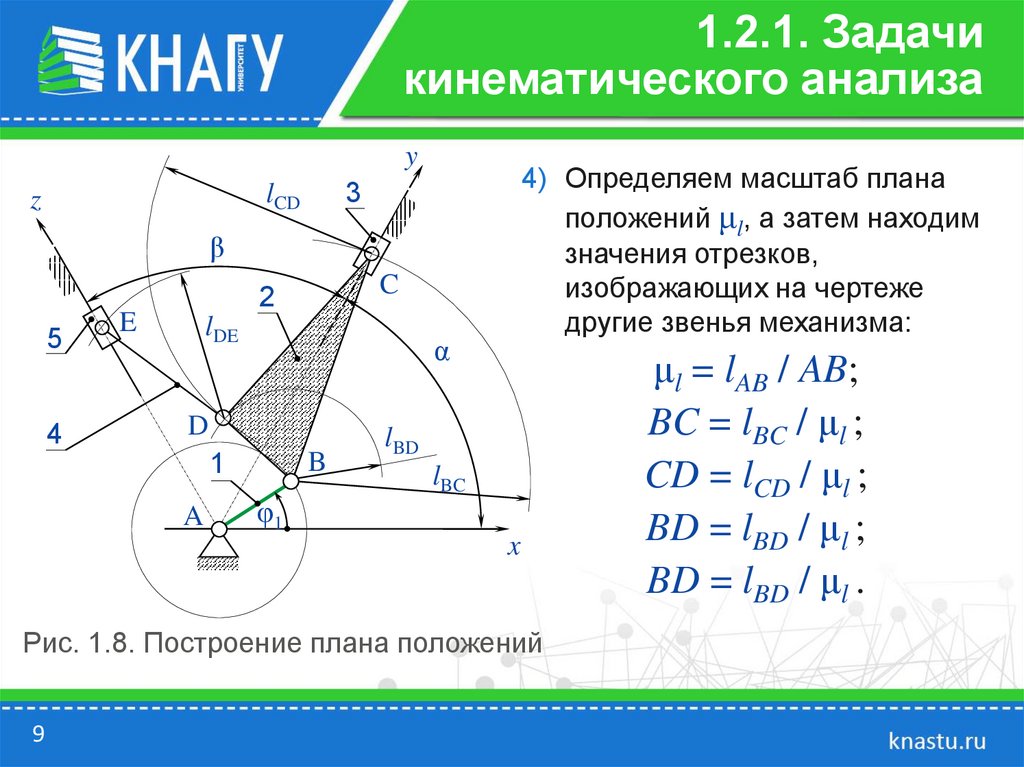
4) Определяем масштаб плана
положений μl, а затем находим
значения отрезков,
изображающих на чертеже
другие звенья механизма:
3
lCD
z
β
5
4
C
2
E
lDE
α
D
B
1
A
lBD
lBC
φ1
x
Рис. 1.8. Построение плана положений
9
μl = lAB / AB;
BC = lBC / μl ;
CD = lCD / μl ;
BD = lBD / μl ;
BD = lBD / μl .
10.
1.2.1. Задачикинематического анализа
y
3
lCD
z
β
5
C
2
E
lD
α
E
4
D
B
1
A
φ1
lBD
lB
C
x
5) Отмечаем на чертеже
положения неподвижных
элементов кинематических пар:
шарнира А и направляющих
Ay и Az.
6) Строим положение ведущего
звена по заданной обобщенной
координате φ1.
7) Строим положения групп
Ассура в порядке
их присоединения к ведущему
звену.
Рис. 1.8. Построение плана положений
10
11.
1.2.1. Задачикинематического анализа
• Если построить ряд последовательных положений
ведущего звена
и изобразить на том же чертеже соответствующие
положения групп Ассура, то можно получить
траекторию движения любой точки механизма.
11
12.
1.2.2. Планы скоростейи ускорений
• План скоростей (ускорений) механизма – это чертеж,
на котором изображены в виде отрезков векторы,
равные по модулю и направлению скоростям (ускорениям)
различных точек звеньев механизма
в данный момент времени.
• План скоростей (ускорений) механизма представляет собой:
‒ совокупность нескольких планов скоростей (ускорений)
отдельных звеньев,
‒ у которых полюса планов р являются общей точкой –
полюсом плана скоростей (ускорений) механизма.
12
13.
1.2.2. Планы скоростейи ускорений
• Планы скоростей и ускорений механизма строятся:
‒ после решения задачи о его положениях
применительно к группам Ассура,
которыми образован исследуемый механизм.
• Кинематический анализ механизма начинается с ведущего
звена, закон движения которого задан,
и заканчивается построением планов скоростей
и ускорений для последней присоединенной группы Ассура,
т.е. проводится в порядке образования механизма.
13
14.
1.2.2. Планы скоростейи ускорений
• При сложном движении точки или тела движение
исследуется одновременно
‒ в основной
‒ и подвижной системах отсчета.
• Абсолютное движение ‒ движение точки или тела
по отношению к основной системе отсчета.
• Относительное движение ‒ движение точки или тела
по отношению к подвижной системе отсчета.
• Переносное движение ‒ движение подвижной системы
отсчета по отношению к основной системе отсчета.
14
15.
1.2.2. Планы скоростейи ускорений
Теорема о сложении скоростей при сложном
движении точки:
абсолютная скорость точки
равна геометрической сумме переносной
и относительной скоростей этой точки
v a ve v r .
15
(1.2)
16.
1.2.2. Планы скоростейи ускорений
• При определении переносной скорости точки
предполагается, что относительное движение остановлено.
• При плоском движении звена:
‒ переносное движение ‒ поступательное движение
со скоростью произвольно выбранной точки звена,
принятой за полюс,
‒ относительное движение ‒ вращательное
вокруг этой точки (полюса),
причем угол и направление поворота не зависят
от выбора полюса.
16
17.
1.2.2. Планы скоростейи ускорений
Абсолютное ускорение любой точки звена при
плоскопараллельном движении равно геометрической сумме
двух ускорений: ускорения в поступательном переносном
движении и ускорения во вращательном относительном
движении
n
aa ae ar ae ar ar ,
где
(1.3)
arn – нормальное ускорение в относительном вращательном
движении, направленное по радиусу траектории движения
точки к центру ее кривизны;
ar – касательное ускорение, направленное по касательной
к траектории движения точки.
17
18.
1.2.2. Планы скоростейи ускорений
Если переносное движение при сложном движении звена
или точки не является поступательным,
то абсолютное ускорение aa любой точки звена
равно векторной сумме трех ускорений: переносного ae ,
относительного ar Кориолисова aк ускорений
aa ae ar ак , aк 2 e vr .
18
(1.4)
19.
1.2.2. Планы скоростейи ускорений
Направление Кориолисова ускорения
определяется по правилу Жуковского:
vr
aк
е
‒ необходимо спроектировать вектор
относительной скорости vr на плоскость,
перпендикулярную вектору переносной
угловой скорости е,
‒ и повернуть полученную проекцию
в направлении вращения.
Векторные выражения (1.2), (1.3) и (1.4) используют для построения
планов скоростей и ускорений звена при его движении.
19
20.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
С
А
1
ω1 = const
О
20
2
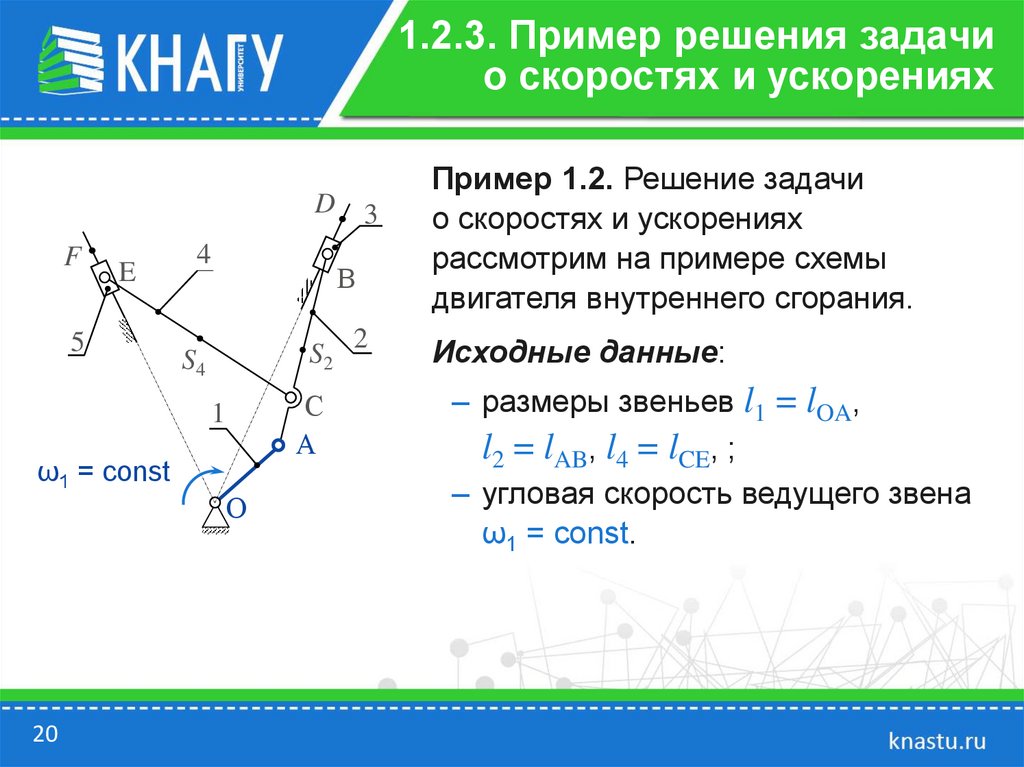
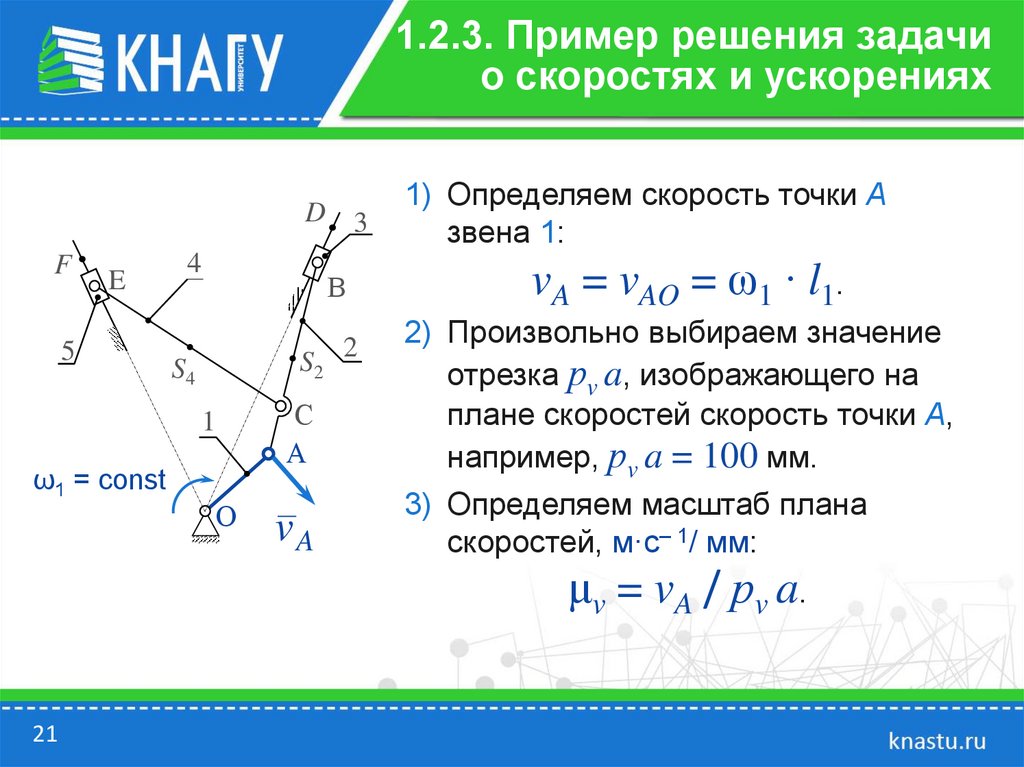
Пример 1.2. Решение задачи
о скоростях и ускорениях
рассмотрим на примере схемы
двигателя внутреннего сгорания.
Исходные данные:
‒ размеры звеньев l1 = lOA,
l2 = lAB, l4 = lCE, ;
‒ угловая скорость ведущего звена
ω1 = const.
21.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
С
А
1
ω1 = const
О
vA
2
1) Определяем скорость точки А
звена 1:
vA = vAO = ω1 ∙ l1.
2) Произвольно выбираем значение
отрезка рv a, изображающего на
плане скоростей скорость точки А,
например, рv a = 100 мм.
3) Определяем масштаб плана
скоростей, м·с– 1/ мм:
μv = vA / рv a.
21
22.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
Оv
v AO
4) Для определения скорости точки В
рассмотрим группу Ассура,
образованную звеньями 2 и 3.
• Для звена 2 в соответствии с (1.2)
скорость точки В определяем
из векторного уравнения
v B v A v BA .
(1.5)
A
• Для звена 3 скорость точки В определяем из уравнения
vB vD vBD ; vD 0.
22
(1.6)
23.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
5
E
4
В
S2
S4
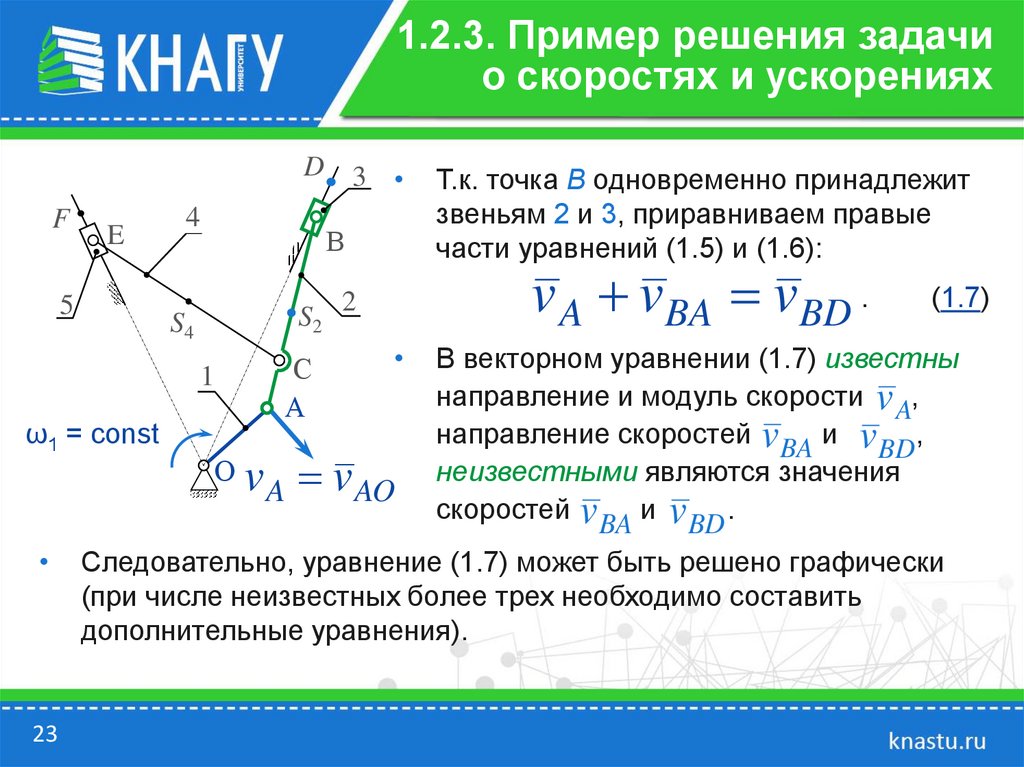
Т.к. точка В одновременно принадлежит
звеньям 2 и 3, приравниваем правые
части уравнений (1.5) и (1.6):
v A vBA vBD .
2
В векторном уравнении (1.7) известны
направление и модуль скорости v A,
направление скоростей v BA и v ,
ω1 = const
BD
Оv v
неизвестными являются значения
A
AO
скоростей v и v .
BA
BD
• Следовательно, уравнение (1.7) может быть решено графически
(при числе неизвестных более трех необходимо составить
дополнительные уравнения).
1
23
С
А
(1.7)
24.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
ω1 = const
О
24
2
С
А
1
pv, o, f, d
v A v AO
v A vBA vBD
Решаем графически уравнение (1.7).
Построение для правой и левой частей уравнения (1.7) начинаем
из полюса плана скоростей рv.
Отмечаем на чертеже положение полюса плана скоростей рv.
25.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
АВ
b
a
v A vBA vBD vB
(1.7)
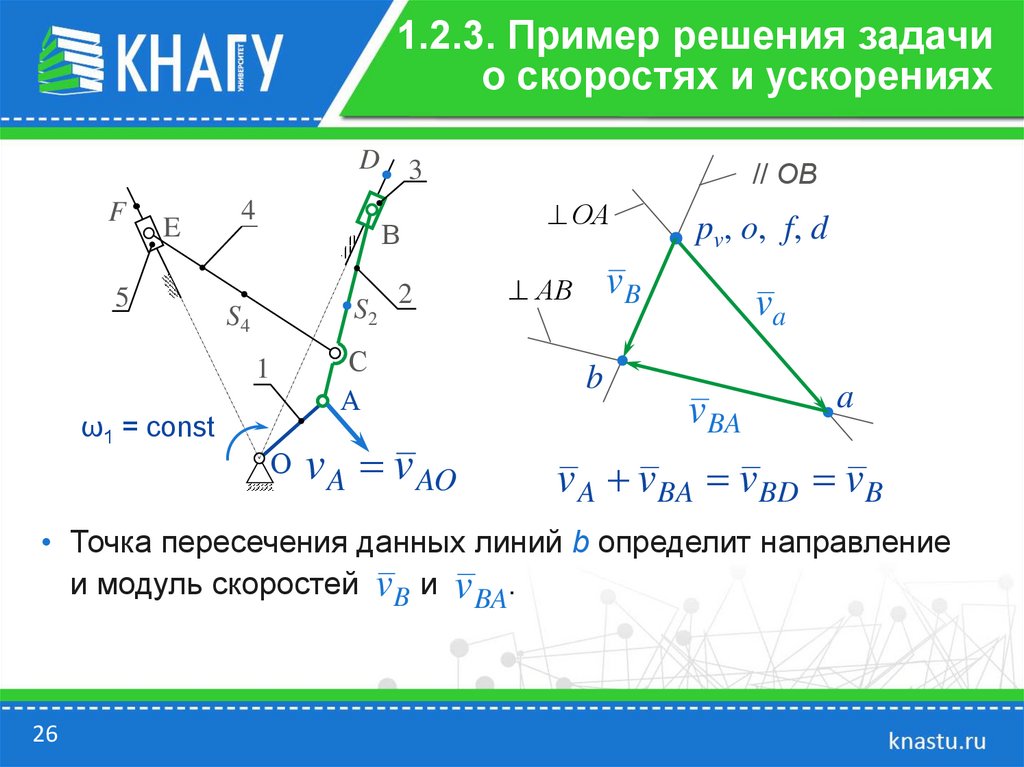
• Из полюса рv проводим отрезок рva перпендикулярно звену ОА.
• Через точку а проводим линию перпендикулярно звену АВ,
по которой направлена скорость v BA, а через полюс плана скоростей
pv проводим линию, параллельную направляющей ползуна 3.
25
26.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
vB
АВ
b
va
v BA
a
v A vBA vBD vB
• Точка пересечения данных линий b определит направление
и модуль скоростей v B и v BA.
26
27.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
vB
АВ
b
va
v BA
a
v A vBA vBD vB
• Измерив на плане скоростей значения отрезков ab и рv b, определим
значения скоростей: v BA ab v ...; v B pv b v ...
• Определяем значение угловой скорости звена 2, рад/с:
27
2 v AB l2 .
28.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
vB
АВ
b
va
v BA
a
5) По аналогии с определением скорости точки В определяем
скорость точки Е.
Для этого рассмотрим группу Ассура, образованную звеньями 4 и 5.
28
29.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
// OB
ОА
pv, o, f, d
vB
АВ
b
va
v BA
a
v A v AO
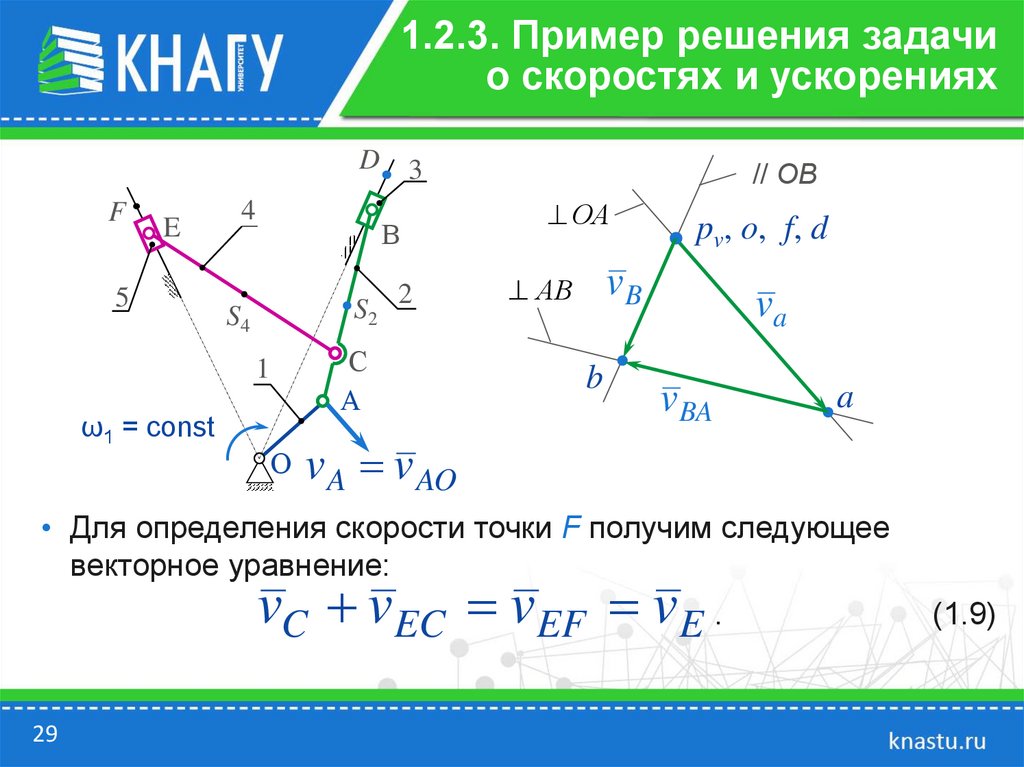
• Для определения скорости точки F получим следующее
векторное уравнение:
vC vEC vEF vE .
29
(1.9)
30.
1.2.3. Пример решения задачио скоростях и ускорениях
D 3
F
E
5
4
В
S2
S4
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
vB
АВ
b
va
v BA
a
vC vEC vEF vЕ
• В векторном уравнении (1.9) более трех неизвестных: модуль
и направление скорости vC , модули скоростей vEC и vEF .
30
31.
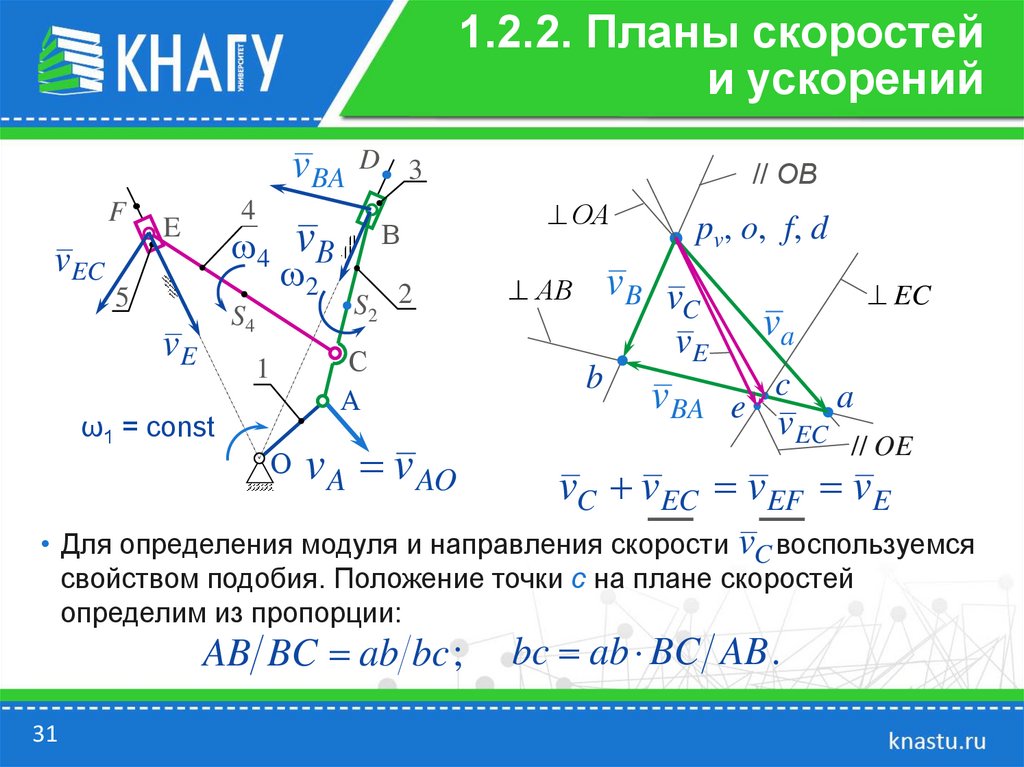
1.2.2. Планы скоростейи ускорений
v BA
F
4
E
4
vEC
5
В
vВ
2
S4
vE
D 3
S2
2
С
А
1
ω1 = const
О
v A v AO
// OB
ОА
pv, o, f, d
vB v
C
АВ
b
vE
EC
va
v BA e c a
vEC
// OE
vC vEC vEF vE
• Для определения модуля и направления скорости vC воспользуемся
свойством подобия. Положение точки с на плане скоростей
определим из пропорции:
AB BC ab bc ;
31
bc ab BC AB .
32.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
E
vEC 5
v BA
3
АВ
В
4
n
aEC
ω4
S4
S2
1
ω1 = const
ω4 = vEC / l4.
n
aBA
ε2
ε4
Значение угловой скорости
звена 4, рад/с:
2
ω2
С
А
n
a AO
О v A v AO
6) Определяем ускорение точки А,
принадлежащей звену 1.
• Поскольку ω1 = const,
ускорение точки А имеет одну
составляющую – нормальное
ускорение, модуль которого
aA
32
n
a AO
2
1
l1
2
vA
l1 .
33.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
E
vEC 5
v BA
n
aEC
4
ω4
S4
ε2
3
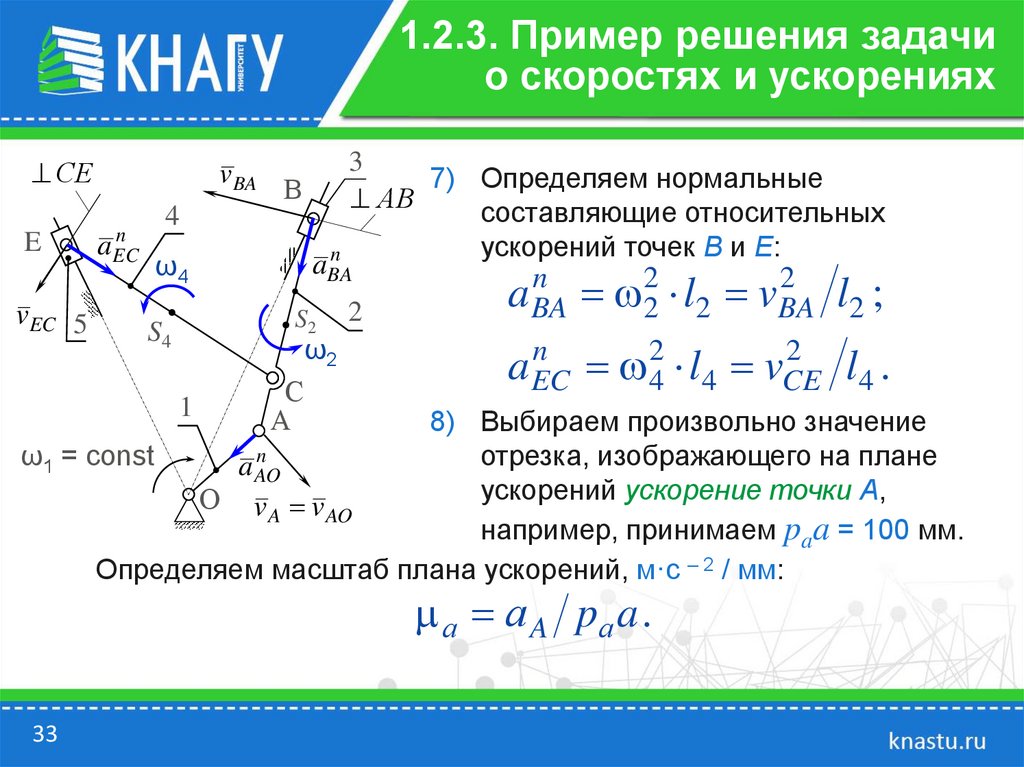
7) Определяем нормальные
В
АВ
составляющие относительных
ускорений точек В и Е:
n
aBA
n
2
2
S2
ε4
1
ω2
С
А
2
a BA 2 l2 vBA l2 ;
n
2
a EC
24 l4 vCE
l4 .
8) Выбираем произвольно значение
n
отрезка, изображающего на плане
ω1 = const
a AO
ускорений ускорение точки А,
О v A v AO
например, принимаем paa = 100 мм.
Определяем масштаб плана ускорений, м·с – 2 / мм:
а а A pа a .
33
34.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
E
vEC 5
v BA
4
n
aEC
ω4
S4
S2
ε4
1
ω1 = const
34
ε2
3
• Определяем значения отрезков,
В
АВ
изображающих на плане ускорений
n
n
ускорения a BA и a EC , мм:
n
aBA
2
ω2
С
А
n
a AO
О v A v AO
n
ab n a BA
а ;
n
сe n a EC
а .
9) Для определения ускорения точки В,
рассмотрим группу Ассура,
образованную звеньями 2 и 3.
• Для звена 2 имеем
n
a B a A a BA a BA . (1.10)
• Для звена 3 имеем
r
к
a B aO a BO
a BO
. (1.11)
35.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
E
vEC 5
v BA
4
n
aEC
ω4
S4
2
ε4
1
ω1 = const
ε2
3
В
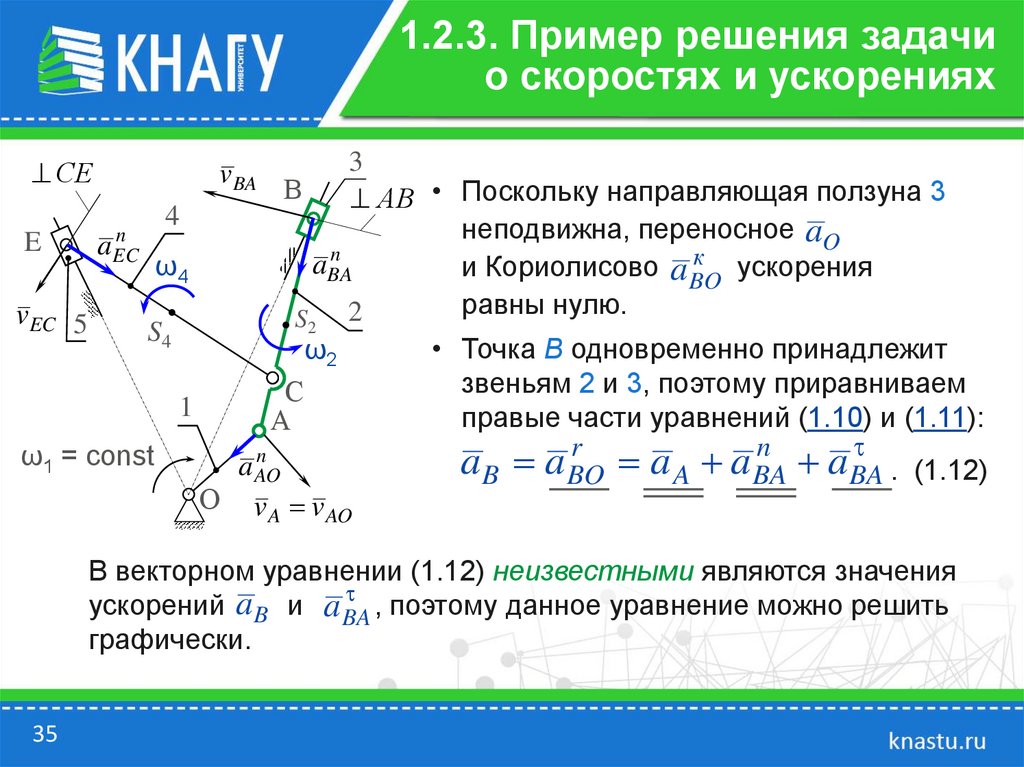
АВ • Поскольку направляющая ползуна 3
неподвижна, переносное aO
n
к
aBA
и Кориолисово a BO
ускорения
равны нулю.
2
S
ω2
С
А
n
a AO
О v A v AO
• Точка В одновременно принадлежит
звеньям 2 и 3, поэтому приравниваем
правые части уравнений (1.10) и (1.11):
r
n
a B a BO
a A a BA
a BA
. (1.12)
В векторном уравнении (1.12) неизвестными являются значения
ускорений a B и a BA
, поэтому данное уравнение можно решить
графически.
35
36.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
v BA
E
vEC 5
В
4
n
aEC
n
aBA
ω4
S2
S4
2
а
aA
ω2
1
ω1 = const
pa
3
АВ
С
А
n
a AO
О v A v AO
r
n
aB aBO
a A aBA
aBA
Строим правую часть уравнения. Отмечаем на чертеже полюс плана
ускорений ра и откладываем из него отрезок раа параллельно звену
n
ОА в направлении ускорения a A a AO.
36
37.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
v BA
E
vEC 5
В
4
n
aEC
S2
ω1 = const
2
ω2
1
aA
n
aBA
ω4
S4
pa
3
АВ
С
А
n
a AO
О v A v AO
АВ
а
n
a BA
bn
r
n
aB aBO
a A aBA
aBA
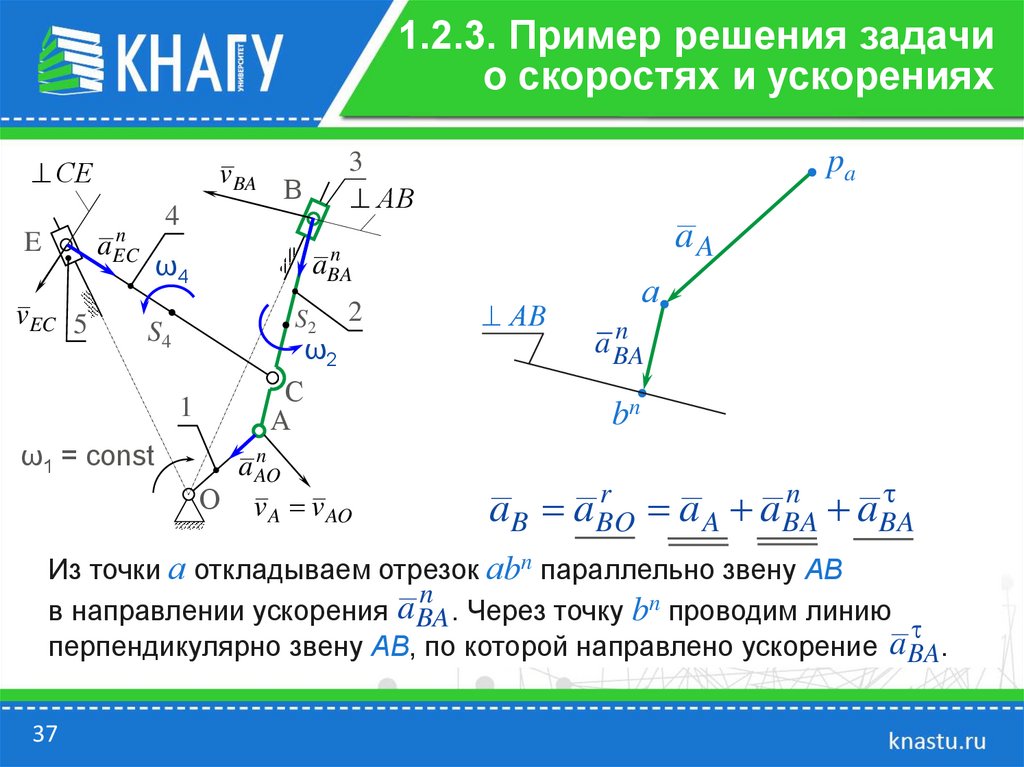
Из точки а откладываем отрезок аbn параллельно звену АВ
n
в направлении ускорения a BA . Через точку bn проводим линию
перпендикулярно звену АВ, по которой направлено ускорение a BA.
37
38.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
v BA
E
vEC 5
В
4
n
aEC
ω4
n
aBA
S2
S4
2
aA
aBA
АВ
ω2
1
ω1 = const
ε2
pa
3
АВ
С
А
n
a AO
О v A v AO
а
aB
n
a BA
bn b
aBA
aB
r
aBO
// OB
n
a A aBA
aBA
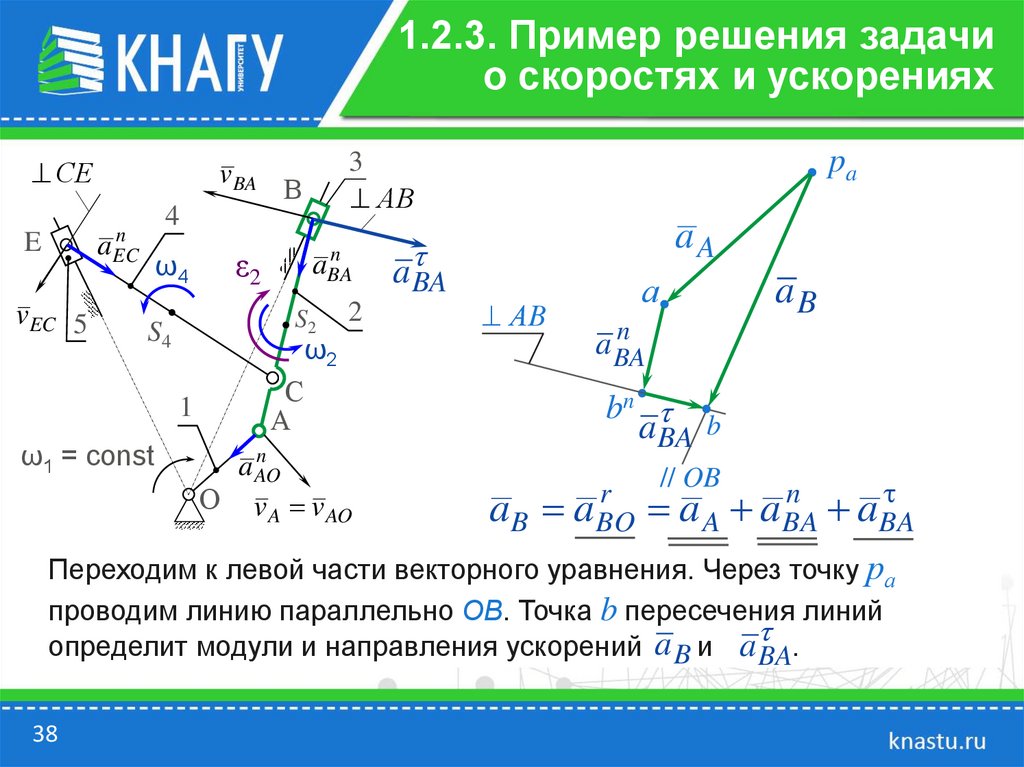
Переходим к левой части векторного уравнения. Через точку ра
проводим линию параллельно OB. Точка b пересечения линий
определит модули и направления ускорений a B и a BA.
38
39.
1.2.3. Пример решения задачио скоростях и ускорениях
СЕ
E
vEC 5
v BA
a EC
В
4
n
aEC
ε2
ω4
S4
n
aBA
S2
ε4
1
ω1 = const
О
2
ω2
С
А
n
a AO
pa
3
АВ
v A v AO
aA
aBA
АВ
а aС
n
a BA
с
bn b
aBA
СЕ
aE
aS 4
aB
s4
n
a EC
a EC
e
// OE
en
// OB
r
n
a E a EO
aC a EC
a EC
10) Для определения ускорения точки Е, рассмотрим группу Ассура,
образованную звеньями 4 и 5. Для определения ускорения точки Е
соединим на плане ускорений точки a и b.
39
40.
Россия, 681013, Хабаровский край,г. Комсомольск-на-Амуре, проспект Ленина, 27
+7 (4217) 53-23-04
office@knastu.ru
http://knastu.ru



























 physics
physics








