Similar presentations:
Устойчивость упругих систем
1. Лекция
Устойчивость упругих систем1. Понятие об устойчивости;
2. Формула Эйлера;
3. Формула Ясинского;
4. Диаграмма критических напряжений;
5. Инженерный способ расчета на устойчивость.
Устойчивым следует считать такое состояние механической системы, при
котором любое внешнее отклонение от состояния равновесия вызывает
реакцию системы, восстанавливающую это равновесие.
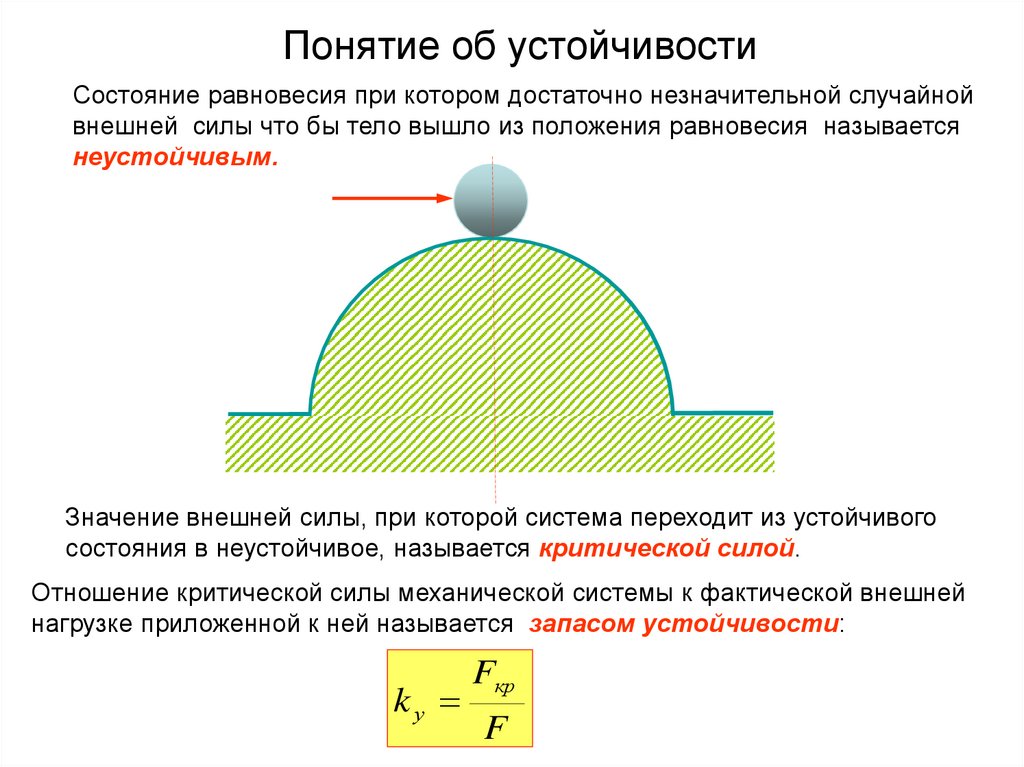
2. Понятие об устойчивости
Состояние равновесия при котором достаточно незначительной случайнойвнешней силы что бы тело вышло из положения равновесия называется
неустойчивым.
Значение внешней силы, при которой система переходит из устойчивого
состояния в неустойчивое, называется критической силой.
Отношение критической силы механической системы к фактической внешней
нагрузке приложенной к ней называется запасом устойчивости:
kу
Fкр
F
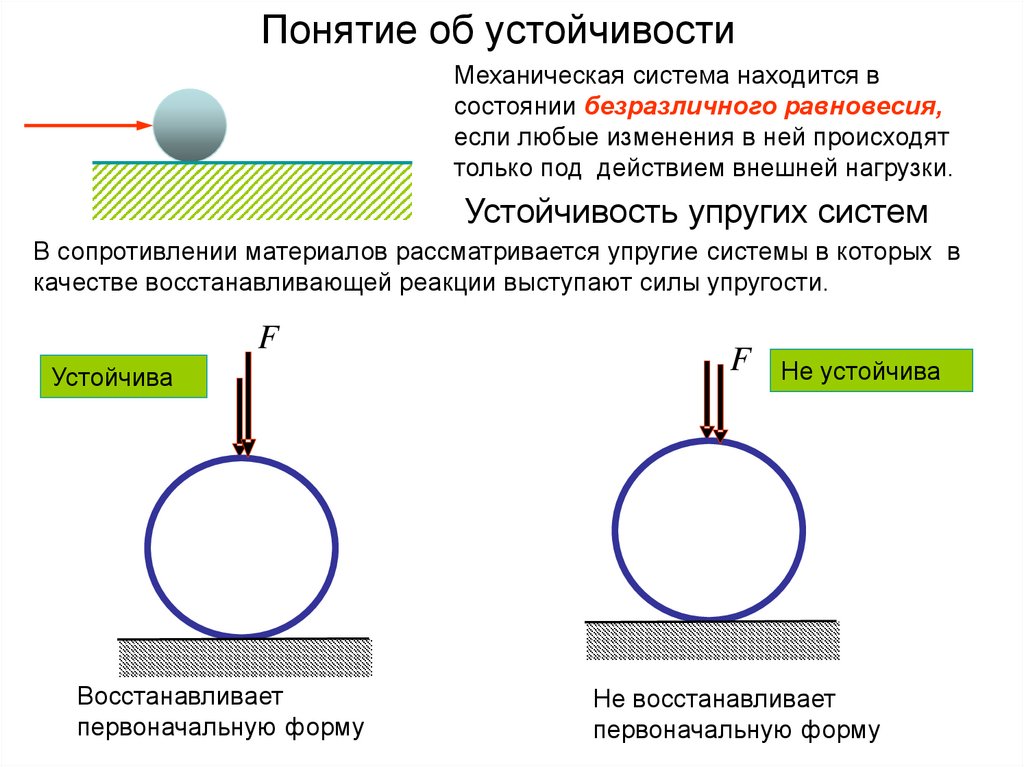
3. Понятие об устойчивости
Механическая система находится всостоянии безразличного равновесия,
если любые изменения в ней происходят
только под действием внешней нагрузки.
Устойчивость упругих систем
В сопротивлении материалов рассматривается упругие системы в которых в
качестве восстанавливающей реакции выступают силы упругости.
F
Устойчива
Восстанавливает
первоначальную форму
F
Не устойчива
Не восстанавливает
первоначальную форму
4. Понятие об устойчивости
Брус нагруженный осевой сжимающейсилой называется стойкой.
Не устойчива
F
F
Стойка, как правило, имеет трубчатое
и коробчатое сечение, также часто
используются составн6ые сечения из
прокатных профилей
Не восстанавливает
первоначальную форму
Восстанавливает
первоначальную
форму
Устойчива
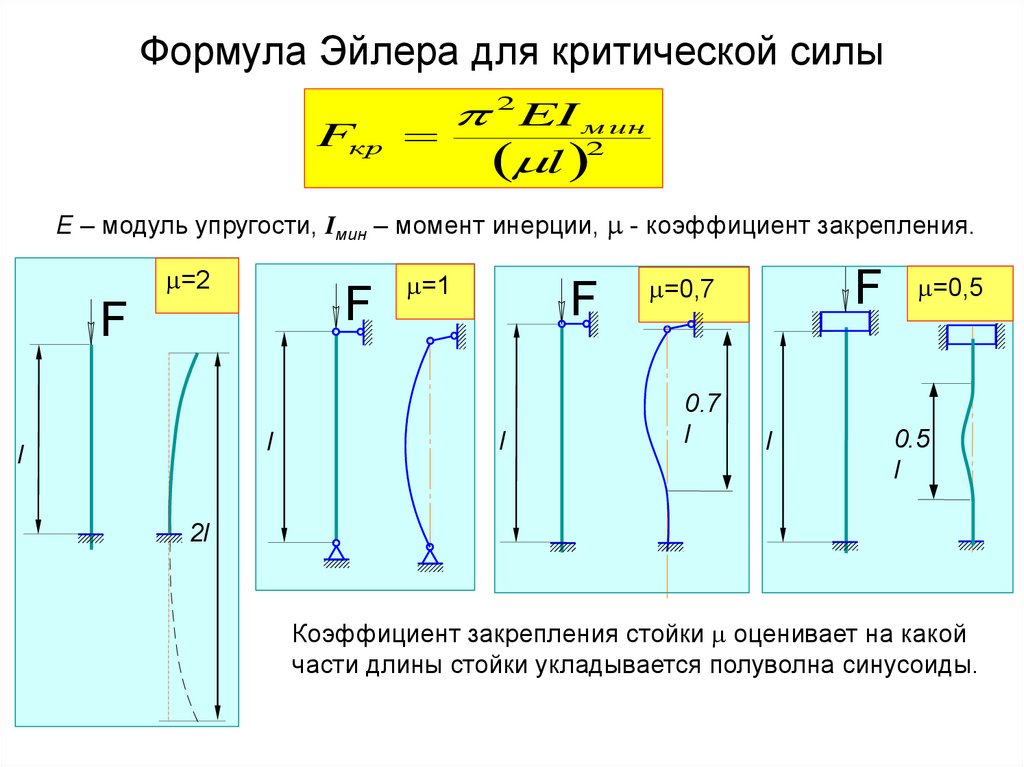
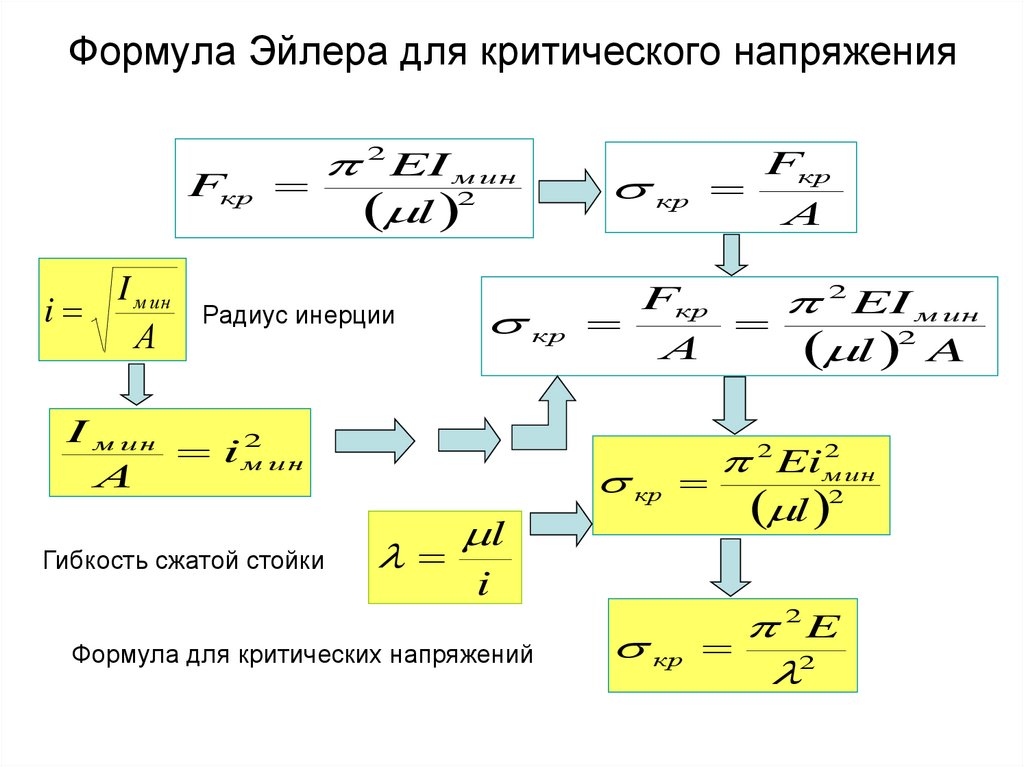
5. Формула Эйлера для критической силы
Fкр2 EI м ин
l 2
Е – модуль упругости, Iмин – момент инерции, - коэффициент закрепления.
=2
F
F
l
l
=1
F
l
F
=0,7
0.7
l
l
=0,5
0.5
l
2l
Коэффициент закрепления стойки оценивает на какой
части длины стойки укладывается полуволна синусоиды.
6. Формула Эйлера для критического напряжения
Fкрi
I м ин
А
2 EI м ин
l 2
Радиус инерции
кр
I м ин
2
iм
ин
А
Гибкость сжатой стойки
кр
Fкр
2 EI м ин
А
l 2 A
кр
l
2 Eiм2 ин
l 2
i
Формула для критических напряжений
Fкр
А
кр
2E
2
7. Пределы применимости формулы Эйлера
кр2E
2
Формула Эйлера для
критических напряжений
Формула Эйлера применима при условии если напряжения не превышают
пределе пропорциональности пц .
кр
2E
2 пц
Условие применимости формулы Эйлера
Выразим из этой формулы гибкость стойки
2
Е
2
пц
Е
Примем следующее обозначение пр
пц
пр
или
получим:
Условие применимости формулы Эйлера
пр - предельная гибкость стойки, зависит только от свойств материала.
Для стали Ст.3: Е=2·105 МПа, пц=200 МПа, пр 100.
Для стали Стали 45: Е=2·105 МПа, пц=400 МПа, пр 70.
Е
пц
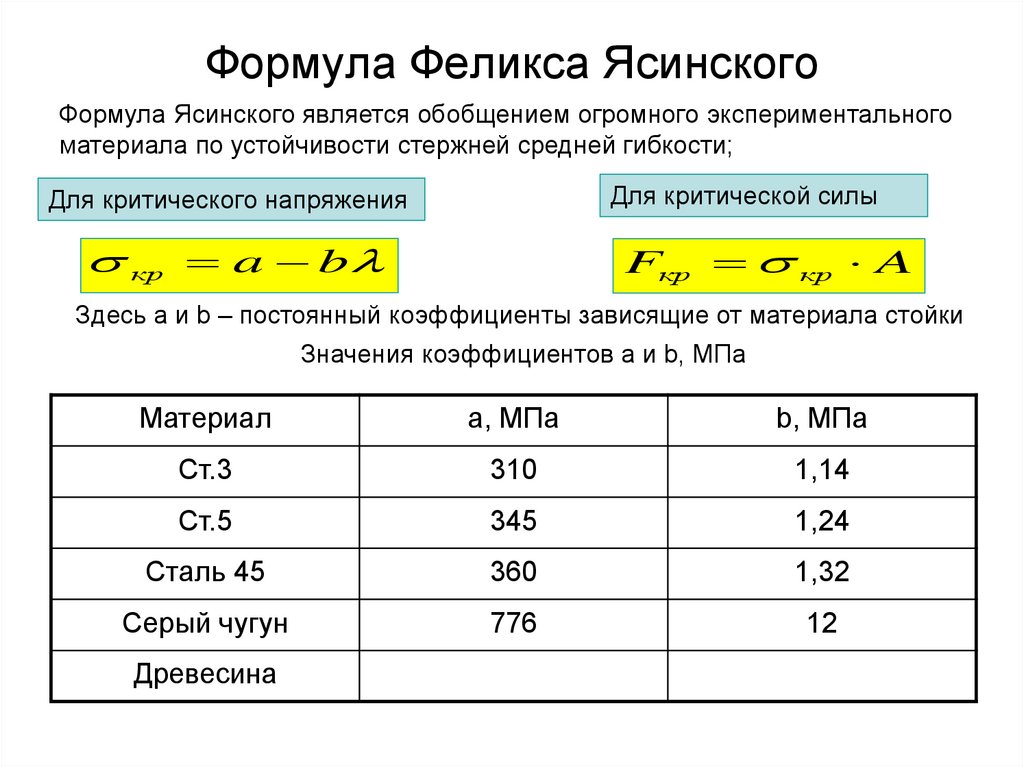
8. Формула Феликса Ясинского
Формула Ясинского является обобщением огромного экспериментальногоматериала по устойчивости стержней средней гибкости;
Для критической силы
Для критического напряжения
кр a b
Fкр кр A
Здесь a и b – постоянный коэффициенты зависящие от материала стойки
Значения коэффициентов a и b, МПа
Материал
а, МПа
b, МПа
Ст.3
310
1,14
Ст.5
345
1,24
Сталь 45
360
1,32
Серый чугун
776
12
Древесина
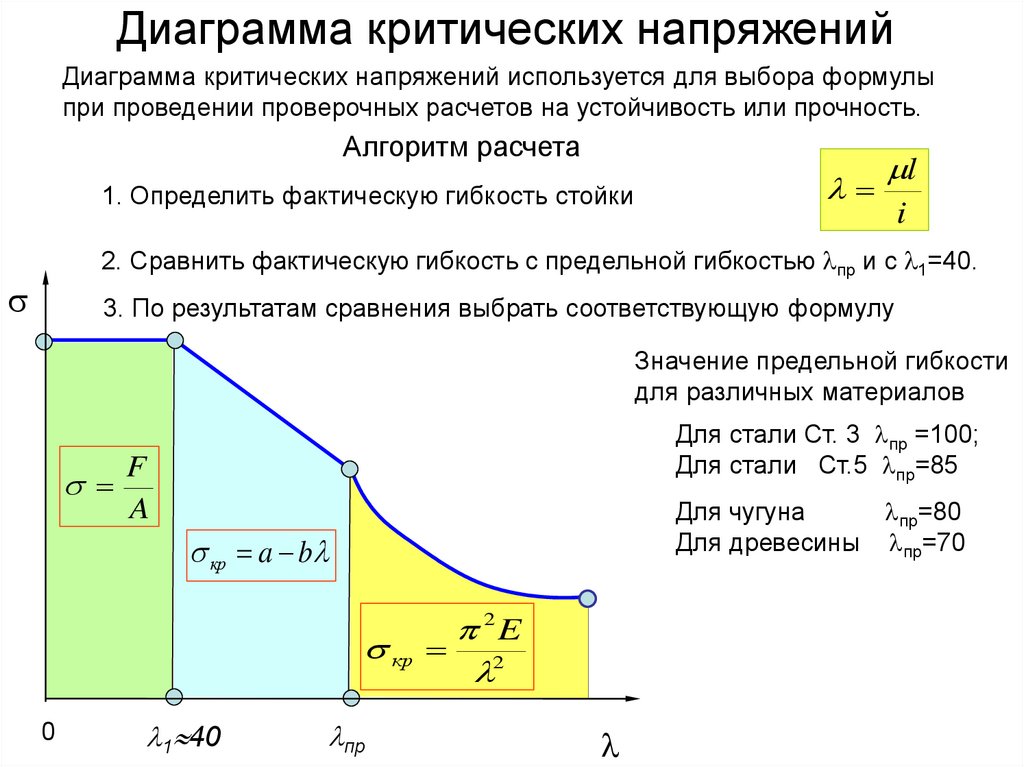
9. Диаграмма критических напряжений
Диаграмма критических напряжений используется для выбора формулыпри проведении проверочных расчетов на устойчивость или прочность.
Алгоритм расчета
1. Определить фактическую гибкость стойки
l
i
2. Сравнить фактическую гибкость с предельной гибкостью пр и с 1=40.
3. По результатам сравнения выбрать соответствующую формулу
Значение предельной гибкости
для различных материалов
Для стали Ст. 3 пр =100;
Для стали Ст.5 пр=85
F
A
Для чугуна
пр=80
Для древесины пр=70
кр a b
кр
0
1 40
пр
2E
2
10. Инженерный способ расчета на устойчивость
Формулы Эйлера и Ясинского используются для выполнения проверочныхрасчетов конструкций на устойчивость.
Для выполнения проектных расчетов используется специальная методика
основанная на использовании коэффициента понижения допускаемого
напряжения
Условие устойчивости записывается в следующем виде
Проверочный расчет
F
A
Проектный расчет
A
F
Алгоритм выполнения проектного расчета проще показать на
конкретном примере.
Дано: Сжимающая сила F=50 кН, длина стойки L=2,0 м, стойка имеет
круглое поперечное сечение, материал Ст.3, допускаемое напряжение
[ ]=100 МПа. Обе опоры стойки шарнирные ( =1).
Определить размеры поперечного сечения стойки.
11. Инженерный способ расчета на устойчивость
Алгоритм выполнения проектного расчетаПеред началом расчета неизвестны геометрические размеры поперечного
сечения стойки, а следовательно нет возможности определить гибкость
стойки и коэффициент . Принимаем любое значение от 0 до 1.
1. Первое значение коэффициента :
1=0,5
2. Площадь сечения стойки в
первом приближении:
A1
3. Геометрические размеры
поперечного сечения
d
4. Радиус инерции сечения
5. Фактическая гибкость стойки:
imin
F
1
4A
50000
1000 мм 2
0,5 100
4 1000
35,69 мм
3,14
I min
4 d 4
d
9 мм.
2
A
4
32 d
l
i min
1 2000
222
9
12. Инженерный способ расчета на устойчивость
6. По значению фактической гибкости стойки 1=222 из таблицы выбираемзначение коэффициента точного значения нет поэтому нужно:
a) Из таблицы гибкости =190 соответствует значение (190)=0,21;
b) Гибкости =200 - (200)=0,19;
c) На десять единиц гибкости приходится =0,02
d) На 22 единицы гибкости приходится =0,02 ·22/10=0,044,
e) (222)=0,19-0,044=0,146.
Условия т1= 1не выполняется и нужно повторить
расчет приняв новое значение коэффициента 2.
т1=0,146< 1=0,5
Гибкость
стойки
0
1,0
0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75 0,69
Гибкость
стойки
100
110
10
20
120
30
130
40
140
50
150
160
60
170
70
180
80
190
90
200
0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19
13. Инженерный способ расчета на устойчивость
7. Второе значение коэффициента :8. Площадь сечения стойки во
втором приближении:
9. Геометрические размеры
поперечного сечения
1 T 1
0,146 0,5
2
0,323
2
2
F
50000
A2
1548 мм 2
2 0,323 100
d
imin
10. Радиус инерции сечения
4 A2
l
i min
Условия т2= 2не выполняется и нужно повторить
расчет приняв новое значение коэффициента 3.
Гибкость
стойки
100
110
120
130
140
4 1548
44,4 мм
3,14
I min
4 d 4
d 44,4
11,1 мм.
2
A
4
4
32 d
11. Фактическая гибкость стойки:
150
160
1 2000
180
11,1
т2=0,23< 2=0,323
170
180
190
200
0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19
14. Инженерный способ расчета на устойчивость
12. Третье значение коэффициента :13. Площадь сечения стойки в
третьем приближении:
14. Геометрические размеры
поперечного сечения
d
15. Радиус инерции сечения
imin
16. Фактическая гибкость стойки:
2 T 2
0,323 0,230
0,277
2
2
F
50000
A3
1805 мм 2
3 0,277 100
3
4 1805
48 мм
3,14
I min
4 d 4
d 48
12 мм.
2
A
4 4
32 d
4 A3
l
i min
1 2000
167
12
a) Из таблицы гибкости =160 соответствует значение (160)=0,29;
b) Гибкости =170 - (170)=0,26;
c) НаГибкость
десять единиц гибкости приходится =0,03
100 110 120 130 140 150 160 170 180 190 200
d) Настойки
7 единицы
гибкости приходится =0,03 ·7/10=0,021,
0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23
0,21 0,19
e) (167)=0,29-0,021=0,269.
Т3=0,269
Ошибка:
T 3 3
0,269 0,277
100%
100% 2,98%
T 3
0,269
что допустимо







 mechanics
mechanics








