Устойчивость сжатого стержня

1. УСТОЙЧИВОСТЬ СЖАТОГО СТЕРЖНЯ.

Задачами о прочности элементов конструкций содержание сопротивления материалов не исчерпывается, так как таких расчетов
часто бывает недостаточно для того, чтобы сделать вывод о безопасности существования конструкции. Наряду с проблемой прочности существует проблема устойчивости сооружения.
Инженерные объекты помимо нагрузок, учитываемых расчетом,
всегда подвергаются дополнительным малым воздействиям, которые стремятся вывести данное тело из расчетного состояния равновесия. Если такие малые возмущения вызывают такие же малые
отклонения тела от расчетного состояния, то говорят, что состояние системы является устойчивым, в противном случае – неустойчивым.
В реальных условиях всегда существуют какие-то причины, по
которым может произойти отклонение от исходного равновесного
состояния. Следовательно, возможность перехода к новому состоянию в неустойчивой системе всегда реализуется. В этом слу-чае
говорят, что произошла потеря устойчивости.

2.

Система при потери устойчивости может вести себя по-разному. Обычно происходит переход к некоторому новому положению
равновесия, что в подавляющем большинстве случаев сопровождается большими перемещениями, возникновением пластических
деформаций или полным разрушением. Возможны случаи, когда
система переходит в режим незатухающих колебаний. Явление
потери устойчивости для упругих тел можно наблюдать на целом
ряде примеров.

3.

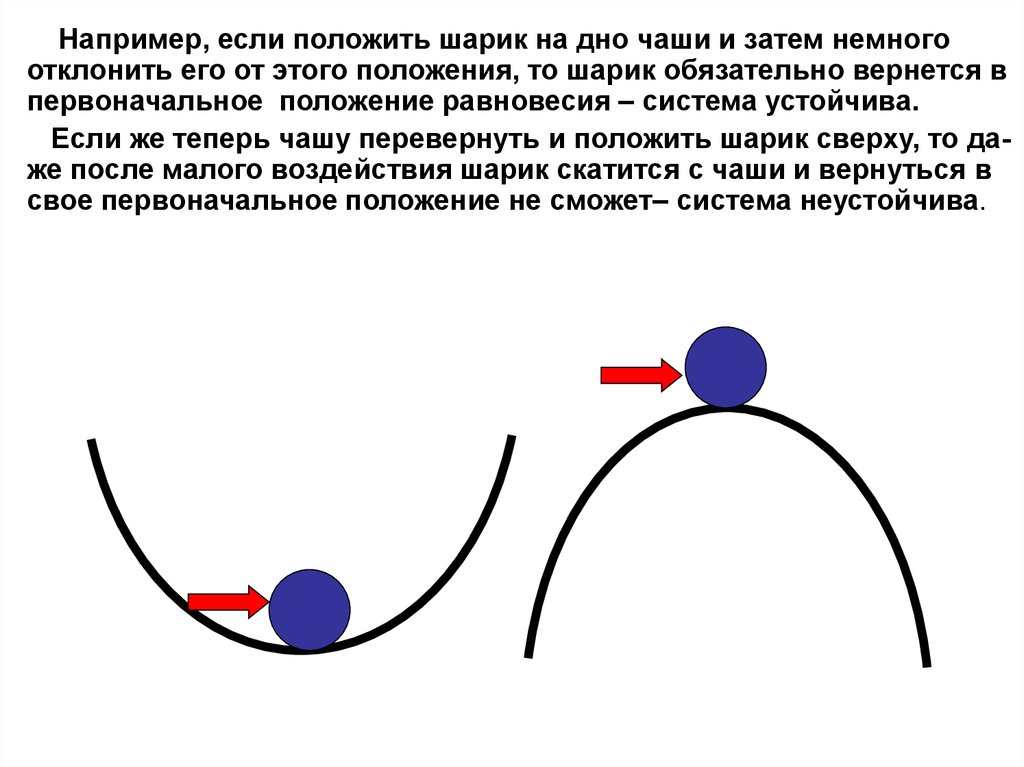
Например, если положить шарик на дно чаши и затем немного
отклонить его от этого положения, то шарик обязательно вернется в
первоначальное положение равновесия – система устойчива.
Если же теперь чашу перевернуть и положить шарик сверху, то даже после малого воздействия шарик скатится с чаши и вернуться в
свое первоначальное положение не сможет– система неустойчива.

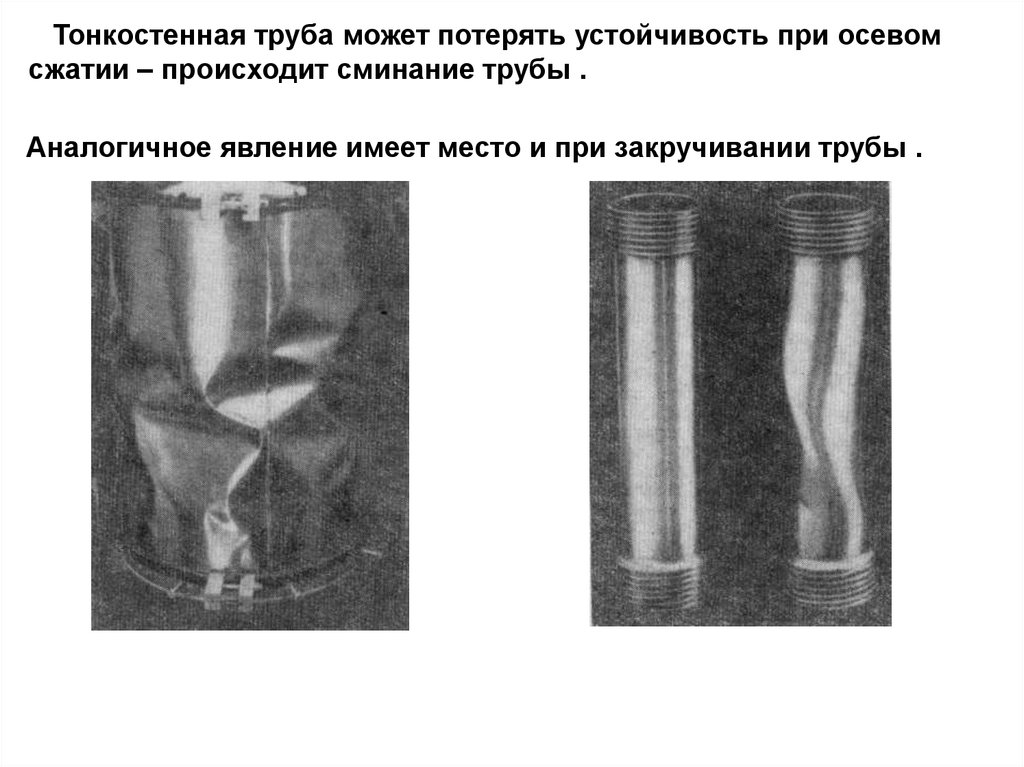
4. Тонкостенная труба может потерять устойчивость при осевом сжатии – происходит сминание трубы .

Аналогичное явление имеет место и при закручивании трубы .

5.

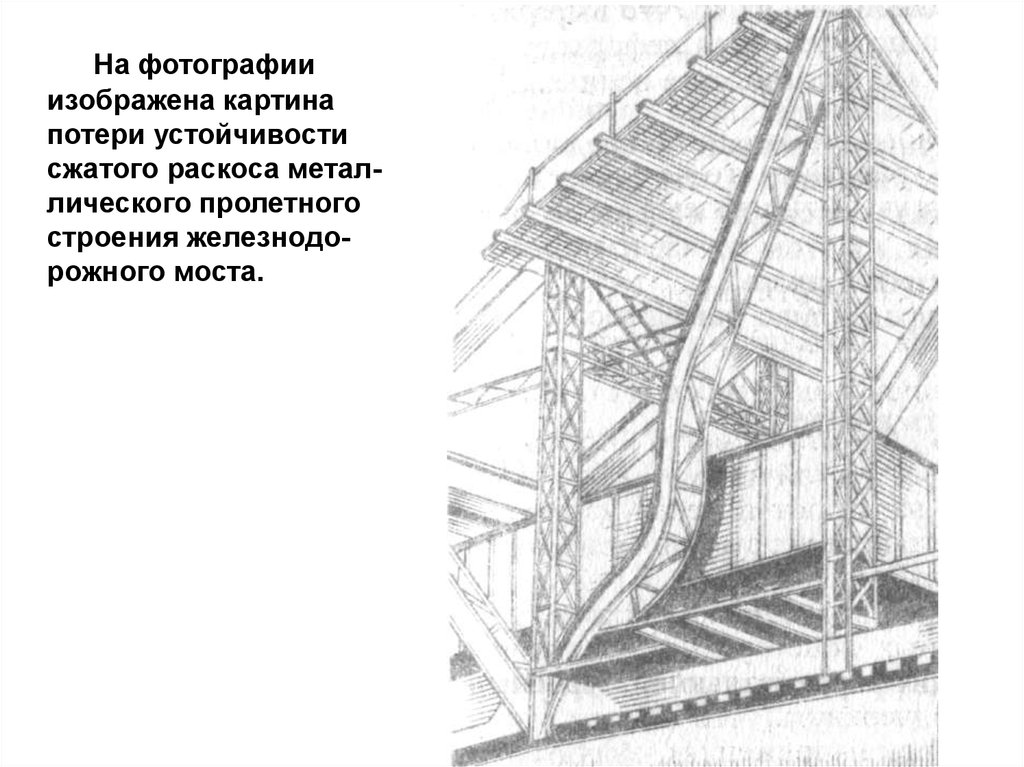
На фотографии
изображена картина
потери устойчивости
сжатого раскоса металлического пролетного
строения железнодорожного моста.

6.

На следующем рисунке показана катастрофа Тэкомского моста.
Строительство Тэкомского моста, имевшего третий в мире по величине пролет – 854м было закончено летом 1940 г.. Движение по
мосту ожидалось небольшое, поэтому пролет сделали очень узкий –11,9м—для двух рядов автомобилей. Полотно моста было
подвешено на двух стальных канатах диаметром 44см каждый.
Катастрофа произошла 7 ноября 1940г. начиная с 8 утра наблюдались не очень сильные вертикальные изгибные колебания при
ветре 17м/сек. Около 10 утра ветер усилился до 18,7м/сек и начались изгибно-крутильные колебания с чрезвычайно большой амплитудой. Когда закрутка достигала максимума, проезжая часть
наклонялась к горизонту под углом 45. Мост выдерживал это около часа, затем часть проезжего полотна отломилась и упала в
воду.

7.

8.

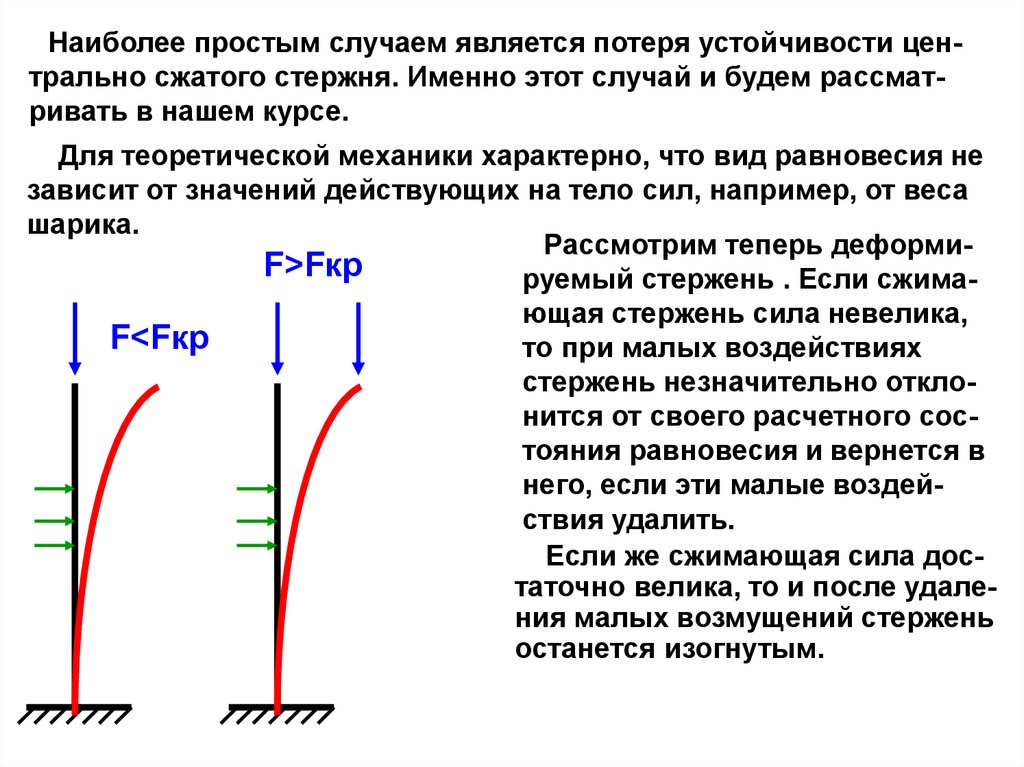
Наиболее простым случаем является потеря устойчивости центрально сжатого стержня. Именно этот случай и будем рассматривать в нашем курсе.
Для теоретической механики характерно, что вид равновесия не
зависит от значений действующих на тело сил, например, от веса
шарика.
Рассмотрим теперь деформиF>Fкр
руемый стержень . Если сжимающая стержень сила невелика,
F<Fкр
то при малых воздействиях
стержень незначительно отклонится от своего расчетного состояния равновесия и вернется в
него, если эти малые воздействия удалить.
Если же сжимающая сила достаточно велика, то и после удаления малых возмущений стержень
останется изогнутым.

9.

Наибольшее значение центрально приложенной сжимающей
силы, до которого устойчива прямолинейная форма равновесия
стержня, называется критической. Если приложенная к стержню
сжимающая сила больше критической, то возникает новая устойчивая форма равновесия – криволинейная.
При F > Fкр , стержень работает на совместное действие сжатия и изгиба. Это состояние стержня называется продольным изгибом. Возникающие при этом деформации и напряжения бывают
недопустимо велики. Если при силе, незначительно большей критической, стержень и не разрушается в буквальном смысле этого
слова, то конструкция все же выходит из строя в результате возникновения больших перемещений .
Появление продольного изгиба опасно тем, что при нем происходит очень сильное нарастание прогибов при малом нарастании
силы. Быстрое нарастание прогибов вызывает нарастание напряжений, что часто приводит к разрушению стержня. Кроме того,
продольный изгиб сжатых стержней особенно опасен еще и потому, что он наступает внезапно. Все сказанное говорит о том, что
все сжатые стержни необходимо рассчитывать не только на прочность, но и на устойчивость, и это принципиально отличает сжатые стержни от растянутых.

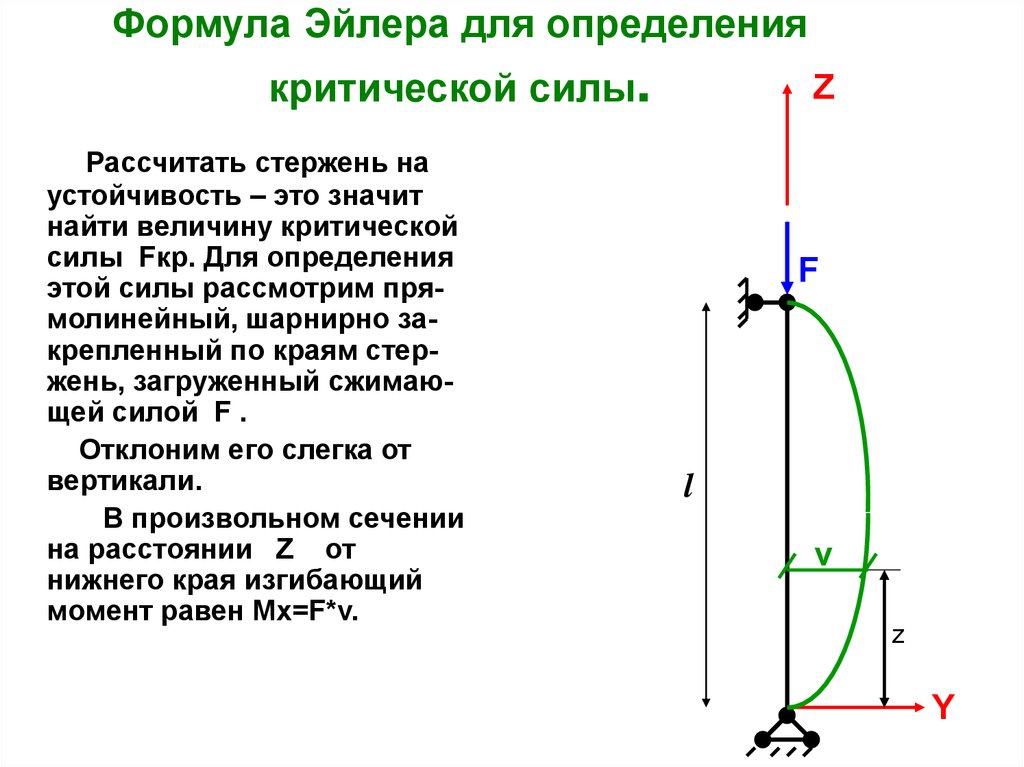
10. Формула Эйлера для определения критической силы.

Рассчитать стержень на
устойчивость – это значит
найти величину критической
силы Fкр. Для определения
этой силы рассмотрим прямолинейный, шарнирно закрепленный по краям стержень, загруженный сжимающей силой F .
Отклоним его слегка от
вертикали.
В произвольном сечении
на расстоянии Z от
нижнего края изгибающий
момент равен Mx=F*v.
Z
F
l
v
z
Y

11.

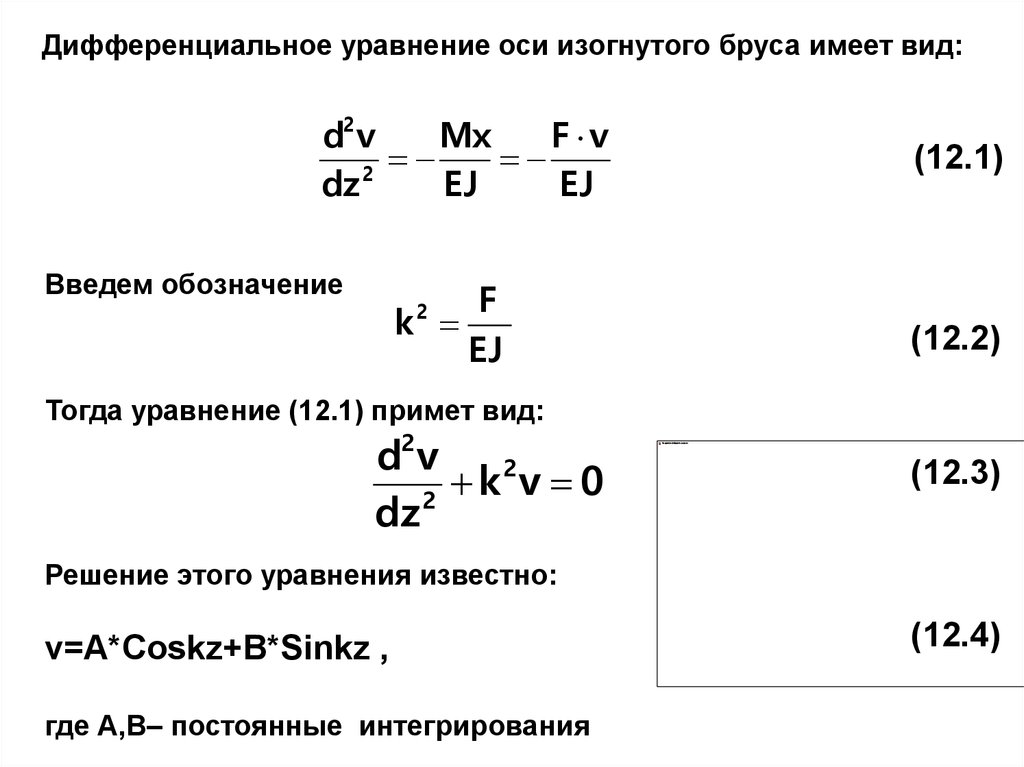
Дифференциальное уравнение оси изогнутого бруса имеет вид:
d2 v
Mx
F v
dz 2
EJ
EJ
Введем обозначение
F
k
EJ
(12.1)
2
(12.2)
Тогда уравнение (12.1) примет вид:
d2 v
2
k v 0
2
dz
(12.3)
Решение этого уравнения известно:
v=A*Coskz+B*Sinkz ,
где А,В– постоянные интегрирования
(12.4)

12.

Найдем их из граничных условий. Так как оба конца стержня
шарнирно оперты, то их перемещения вдоль оси Y будут отсутствовать, то есть
при Z =0 →v=0
(12.5)
при Z = ℓ →v=0
(12.6)
Подставим (12.4) в (12.5) :
v=A*Coskz+B*Sinkz =А*Cos0+В*Sin0=0 →A=0;
Подставим (12.4) в (12.6) :
v=A*Coskz+B*Sinkz =0+В*Sinkℓ=0 → B≠0,
тогда Sin kℓ=0→kℓ=πn; n=1,2,………или
k
n
l

13.

Подставляя найденное значение k в формулу (12.2), найдем величину критической силы, при которой возможно искривление стержня
n
Fкр k EJ EJ
l
2
2
Из (12.4) видно, что прогиб при этом будет равен
n
v Sin z
l
Таким образом, стержень изгибается по синусоиде. При этом, если n=1, то имеем одну полуволну синусоиды, если n=2, то две, и
так далее.

14.

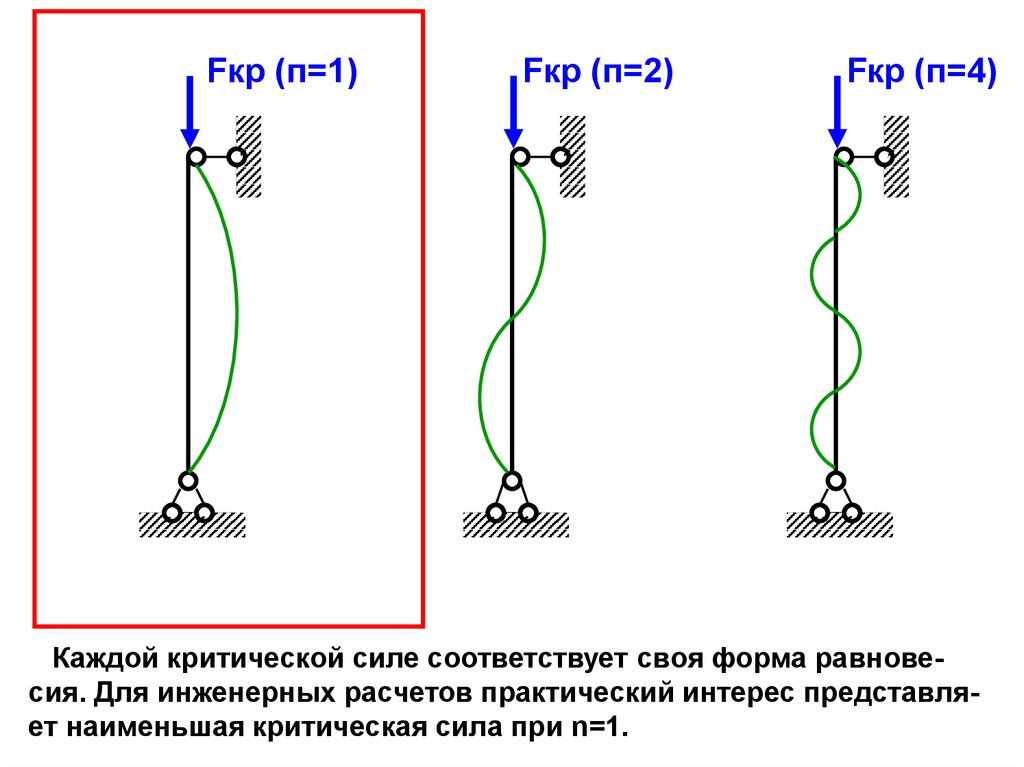
Fкр (п=1)
Fкр (п=2)
Fкр (п=4)
Каждой критической силе соответствует своя форма равновесия. Для инженерных расчетов практический интерес представляет наименьшая критическая сила при n=1.

15.

1
Fкр
0,5
Fкр
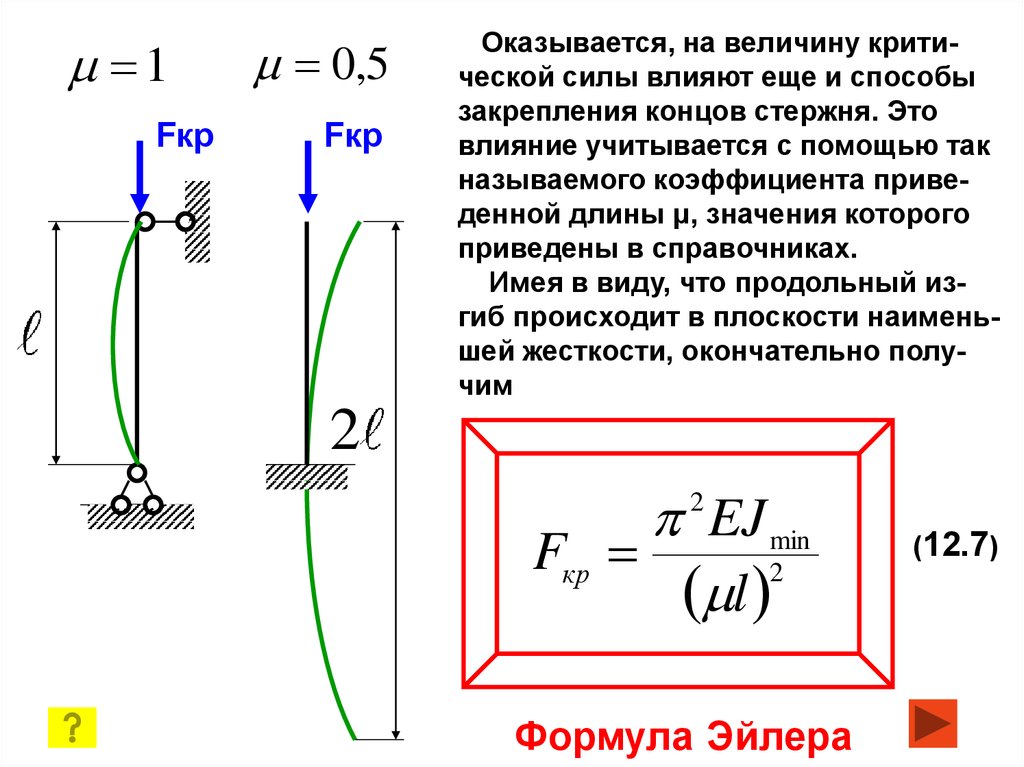
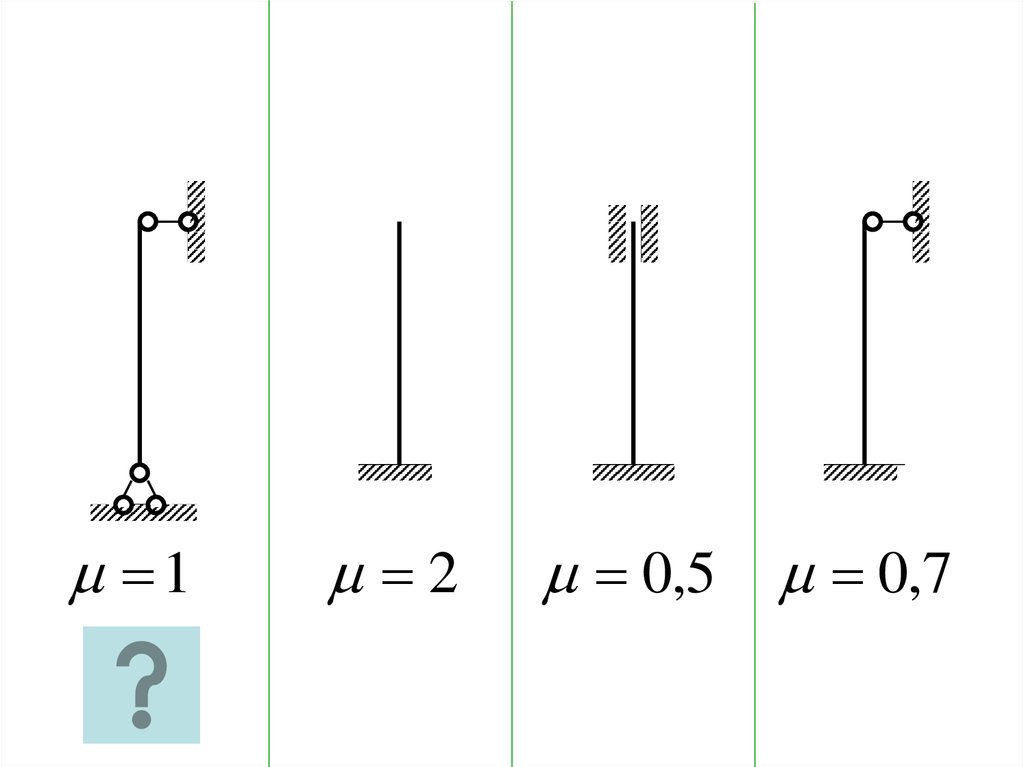
Оказывается, на величину критической силы влияют еще и способы
закрепления концов стержня. Это
влияние учитывается с помощью так
называемого коэффициента приведенной длины μ, значения которого
приведены в справочниках.
Имея в виду, что продольный изгиб происходит в плоскости наименьшей жесткости, окончательно получим
2
EJ min
Fкр
2
l
2
Формула Эйлера
(12.7)

16.

1
2
0,5 0,7

17. Пределы применимости формулы Эйлера.

Значение напряжений, вызываемых в стержне критической силой, также называются критическими. Получим формулу для их
определения:
Fkp
2
2
π
E
i
π EJ min
min
σ kp
2
2
μl A
μl
A
2
Введем новое понятие – гибкости стержня λ:
(12.8)
l
imin
(12.9)
Тогда формула (12.8) перепишется в виде:
σ kp
π 2E
2
λ
(12.10)
Из (12.10) следует, что между критическим напряжением и гибкостью стержня существует гиперболическая зависимость, причем
приλ 0 σ кр

18.

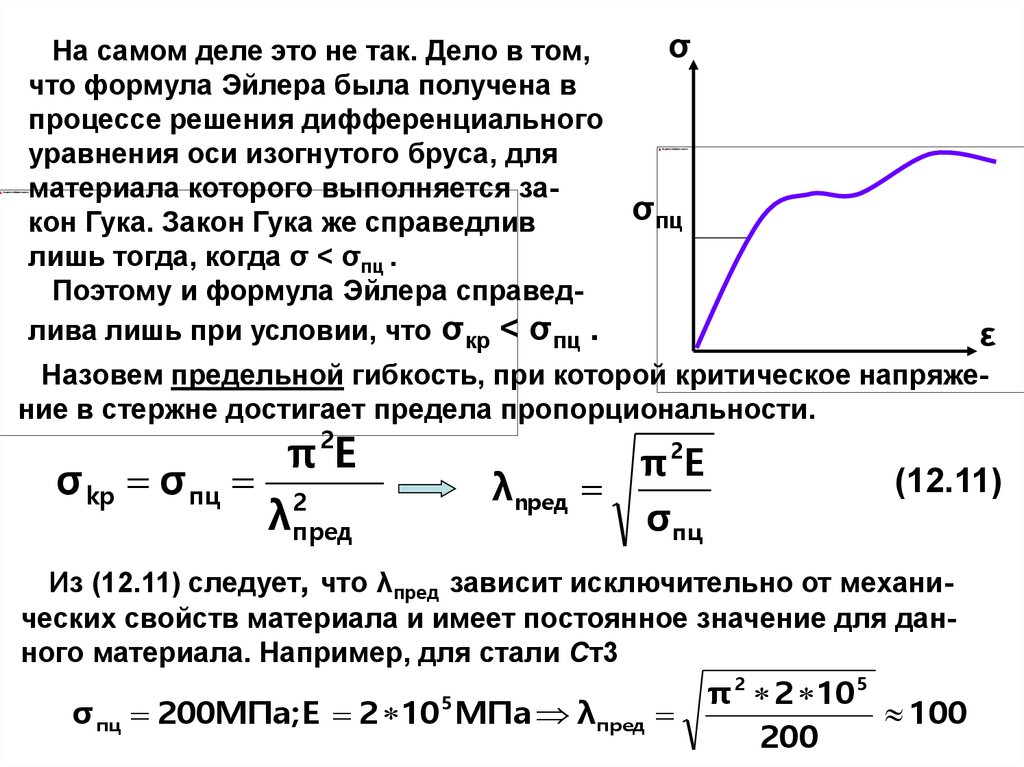
σ
На самом деле это не так. Дело в том,
что формула Эйлера была получена в
процессе решения дифференциального
уравнения оси изогнутого бруса, для
материала которого выполняется заσпц
кон Гука. Закон Гука же справедлив
лишь тогда, когда σ < σпц .
Поэтому и формула Эйлера справедлива лишь при условии, что σкр < σпц .
ε
Назовем предельной гибкость, при которой критическое напряжение в стержне достигает предела пропорциональности.
σ kp
πE
σ пц 2
λпред
2
λnpeд
π 2Е
σ пц
(12.11)
Из (12.11) следует, что λпред зависит исключительно от механических свойств материала и имеет постоянное значение для данного материала. Например, для стали Ст3
σ пц 200МПа;Е 2 10 МПа λпред
5
π 2 2 105
100
200

19.

Таким образом, формула Эйлера применима при
σ кр σ пц ,
или, что тоже самое , при
λ λпред.
(12.12)
При потере устойчивости за пределами зоны упругости критические напряжения определяют по формуле Ясинского :
σ кр a bλ
(12.13)
Здесь а,b – экспериментально установленные параметры , не
имеющие физического смысла и зависящие от материала стержня.
Например, для стали Ст3 -- а=310МПА; b=1,14МПа.
Соответствующая критическая сила определится по формуле:
Fкр σ кр A A a - bλ
(12.14)

20.

Зависимость (12.13) носит линейный характер. Ее можно использовать до некоторого предела, при котором критические напряжения становятся равными опасным. Соответствующее значение гибкости обозначается через λ0. Таким образом,
если σ оп σ кр σ пц , то λ 0 λ λпред
σ оп
σТ
для пластических материалов.
σпч для хрупкихматериалов.
Для стали Ст3
0 30 40.
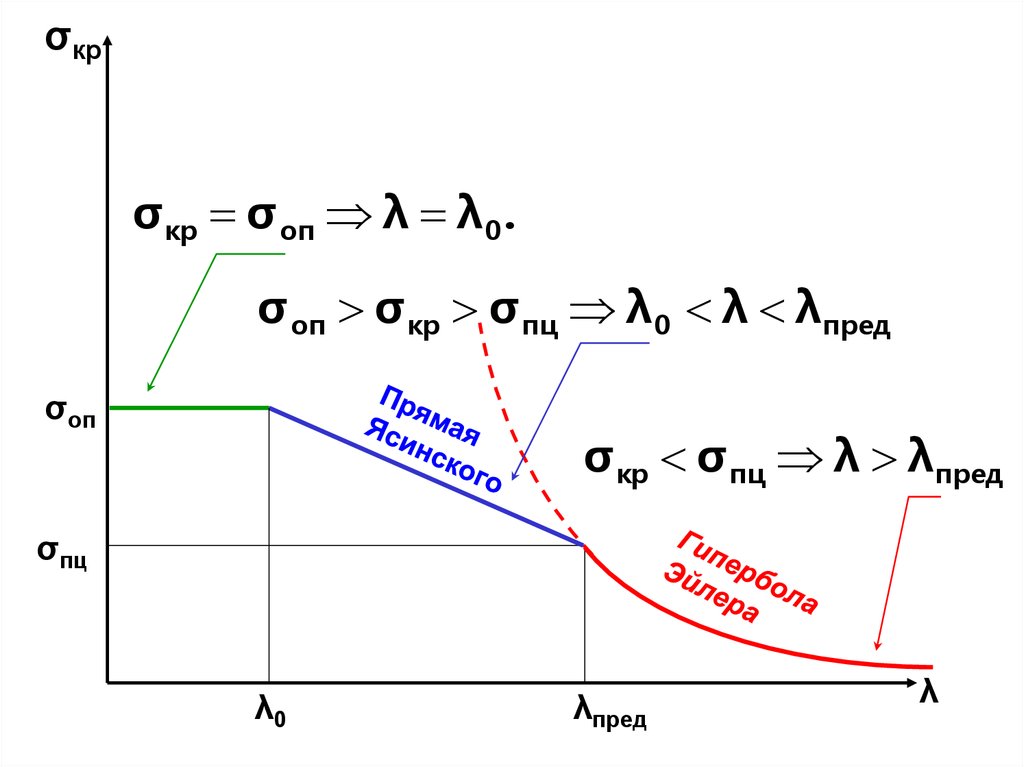
Изобразим графически зависимость критического напряжения от
гибкости стержня:

21.

σкр
σ кр σ оп λ λ 0 .
σ оп σ кр σ пц λ0 λ λпред
σоп
σ кр σ пц λ λпред
σпц
λ0
λпред
λ

22.

Таким образом, все сжатые стержни можно разделить на три
группы:
1. Большой гибкости -- λ>λпред – используется формула
Эйлера.
2. Средней гибкости – λ0<λ<λпред – используется формула
Ясинского.
3. Малой гибкости -- λ0>λ – для таких стержней опасна потеря не
устойчивости, а прочности.

23. Практический метод расчета сжатого стержня на устойчивость.

Для безопасной и надежной работы сжатого стержня необходимо, чтобы сжимающая его сила F не превышала допускаемой
величины F , составляющей некоторую долю от критической
у
силы:
F F У
Fkp
kУ
(12.15)
Здесь kу – коэффициент запаса устойчивости. Его величина зависит от материала, гибкости стержня, условий эксплуатации
конструкции и так далее, и колеблется от 1.5 до 4.
Условие устойчивости стержня (12.15) можно еще переписать в
другом виде:
σу ≤ Rу ,
где
F σ kp
σy
Ry
A ky
(12.16)

24.

Это условие должно выполняться для любого сжатого стержня
наряду с условием прочности:
σ ≤ R , где
F σ on
σ
R
A
n
(12.17)
σоп– опасное напряжение, n– коэффициент запаса прочности, причем kу > n.
Здесь
Обозначим
Ry
σ kp
n
;
R
k y σ on
(12.18)
Коэффициент φ называется коэффициентом продольного изгиба. Он указывает, во сколько раз снижается величина Rу по сравнению с величиной R.
Так как величины n, kу, σкр и σоп зависят от материала стержня, а
σкр и kу – от гибкости его, то и коэффициент φ зависит от гибкости
и материала стержня , причем
0< φ<1, т.к.
σ kp σ on; n k y

25.

Величина φ определяется экспериментально. Она занесена в
специальные таблицы, которые есть в справочниках, в СНИПах и
тому подобное.
Итак, вводя понятие коэффициента продольного изгиба φ, можно
переписать условие устойчивости (12.16) в виде
σ y R y ,или
F
σ y R;
A
F
R
A
(12.19)
Если стержень не имеет местных ослаблений, то при выполнении условия устойчивости (12.19) одновременно выполняется и
условие прочности (12.17). Если такие ослабления ( например, поперечные отверстия) есть, то для ослабленных сечений надо выполнить дополнительный расчет на прочность.

26.

ПРИМЕР.
F=420кн
l=3м
F
Материал – сталь Ст3,
R=210МПа
d
l
0,6d
Для стержня,
изображенного на рисунке,
требуется:
1). Подобрать размеры
поперечного сечения
стержня из условия
устойчивости, используя
метод последовательных
приближений;
2). Определить величину
критической силы;
3). Определить величину
коэффициента запаса
устойчивости.
Из справочника находим значения коэффициента µ. Для данного способа закрепления концов стержня
μ 0,7.

27.

РЕШЕНИЕ.
I. Определим сначала некоторые геометрические характеристики
сечения:
площадь сечения -- A
размер сечения --
π (d
2
(0,6d)
4
2
)
A
d
1,41 A ;
0,5
2
d
(0,6d)
радиус инерции сечения -- i
4
2
0,5d2 ;
(12.20)
(12.21)
0,29d; (12.22)

28.

=
. Найдем гибкость стержня.
Из (12.9) и (12.22)
μ l 0,7 300м 724
λ
.
imin
0,29d
d
(12.23)
≡
. Запишем условие устойчивости (12.19):
F
R; отсюда
σ y R y;
A
F
420кн
20 2
A
см
R 21кн 2
см
(12.24)
Найти площадь сечения непосредственно из (12.24) не удается, так
как для определения φ надо знать гибкость, а для этого нужны размеры сечения, которые неизвестны. Выходим из этого положения,
используя метод последовательных приближений.

29.

≥
. Используем метод последовательных приближений:
1). Берем первое приближение. Так как 0< φ<1 , то берем значение φ посередине между этими значениями:
0
1 0,5;
Из (12.21)
Из (12.23):
Найдем
1
0,5
Из (12.24)
0,74
A1
20
1
1
20
40см2 ;
0,5
d1 1,41 A1 1,41 40 8,92см
724 724
λ1
81
8,92
d1
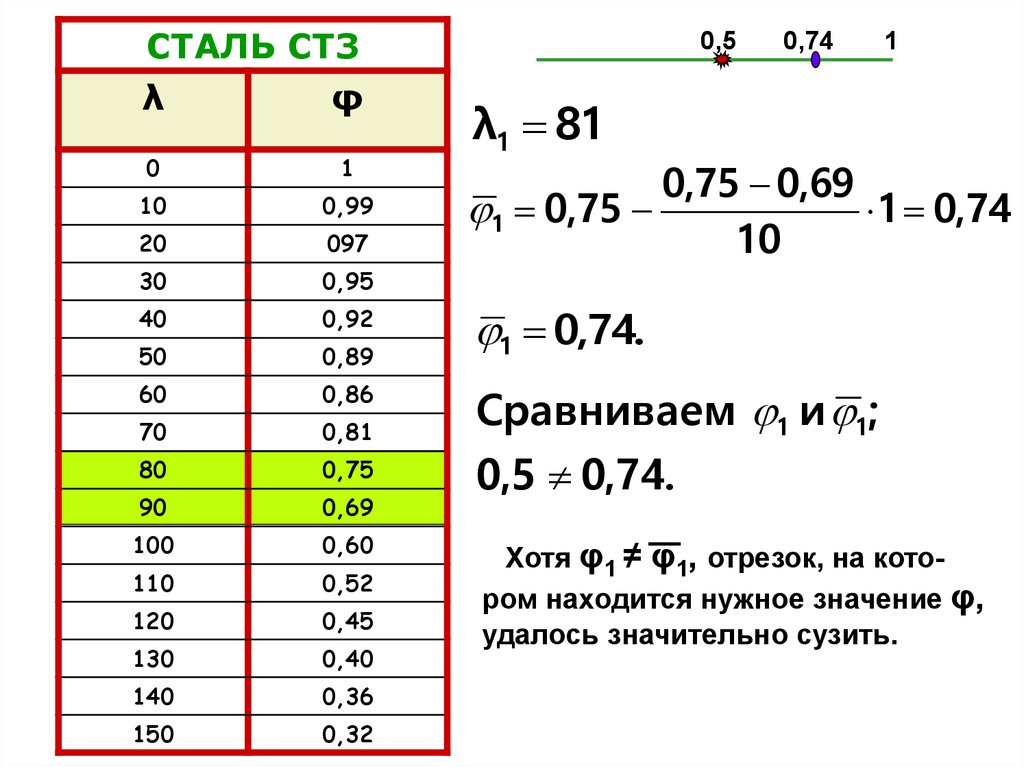
из таблицы с помощью интерполяции:

30.

СТАЛЬ СТ3
λ
φ
0
1
10
0,99
20
097
30
0,95
40
0,92
50
0,89
60
0,86
70
0,81
80
0,75
90
0,69
100
0,60
110
0,52
120
0,45
130
0,40
140
0,36
150
0,32
0,5
0,74
1
λ1 81
0,75 0,69
1 0,75
1 0,74
10
1 0,74.
Сравниваем 1 и 1;
0,5 0,74.
Хотя φ1 ≠ φ1, отрезок, на котором находится нужное значение φ,
удалось значительно сузить.

31.

0
0,5
0,74
1
0,62
2). Берем второе приближение.
Новое значение φ берем посередине нового, суженого, отрезка:
2
1 1
2
0,5 0,74
0,62 .
2
20
20
Далее все вычисления повторяем заново: A 2
32,3см 2 ;
2 0,62
d2 1,41 A2 1,41 32,3 8,01см
724 724
λ2
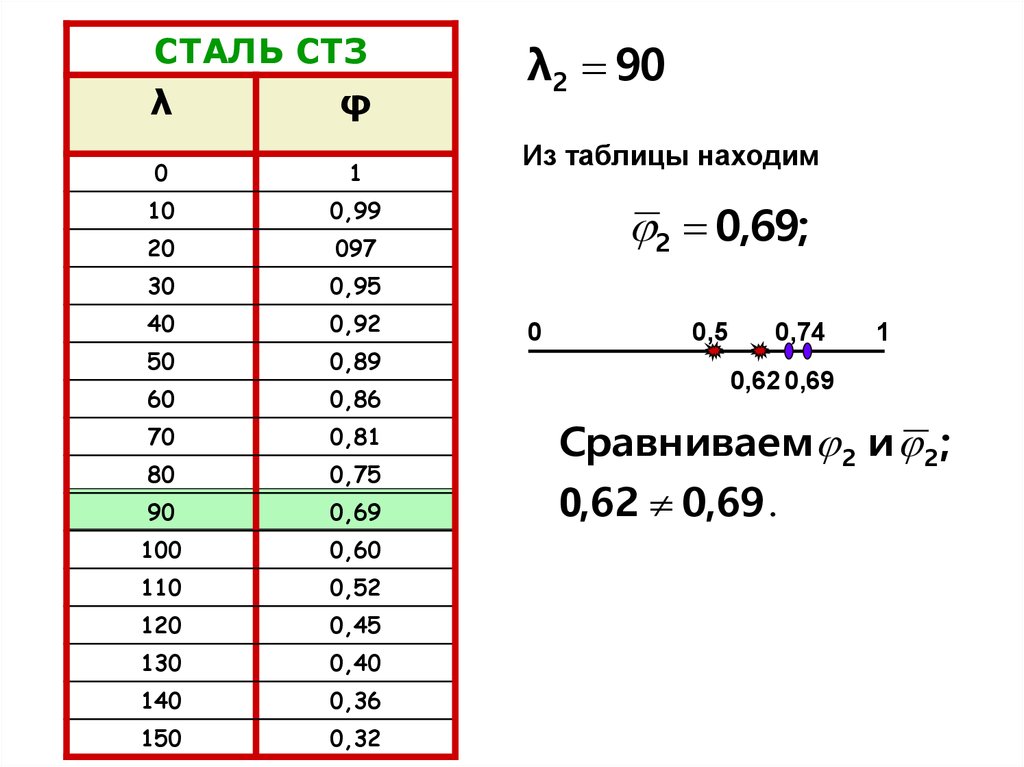
90
d2
8,01

32.

СТАЛЬ СТ3
λ
φ
0
1
10
0,99
20
097
30
0,95
40
0,92
50
0,89
60
0,86
70
0,81
80
0,75
90
0,69
100
0,60
110
0,52
120
0,45
130
0,40
140
0,36
150
0,32
λ2 90
Из таблицы находим
2 0,69;
0
0,5
0,74
1
0,62 0,69
Сравниваем 2 и 2 ;
0,62 0,69 .

33.

3). Берем третье приближение:
3
2 2
2
0
0,62 0,69
0,65 .
2
20
20
A3
30,8см 2 ;
3 0,65
d3 1,41 A3 1,41 30,8 7,82см
724 724
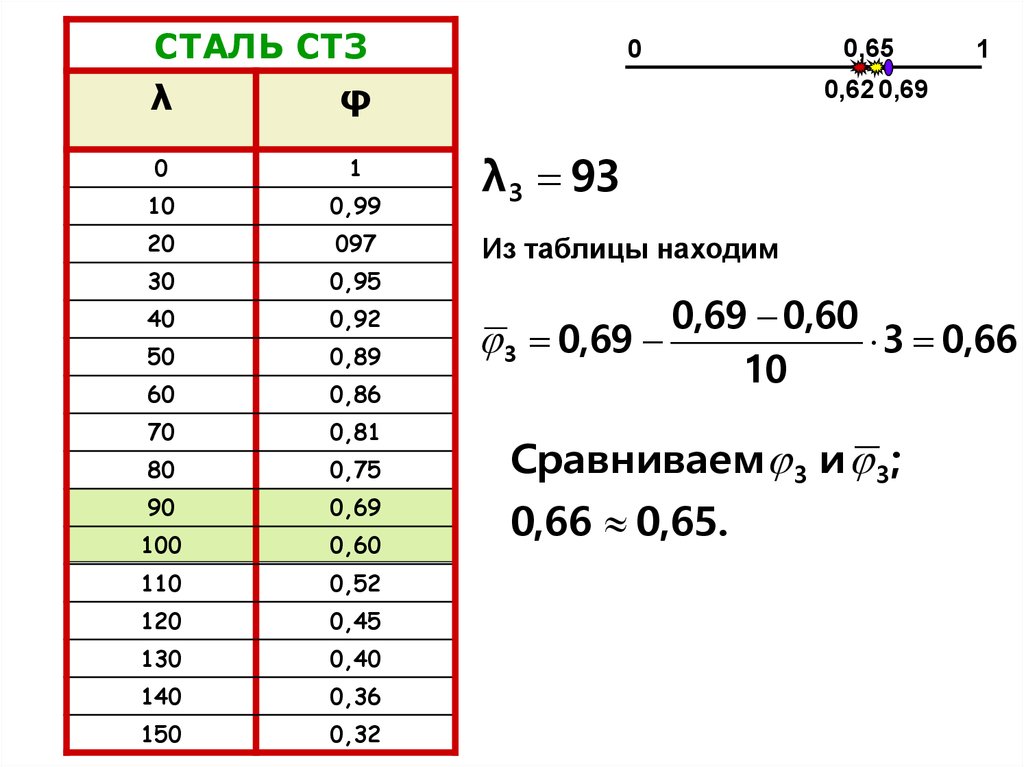
λ3
93
d3
7,82
0,65
0,62 0,69
1

34.

СТАЛЬ СТ3
0
0,65
λ
φ
0
1
10
0,99
20
097
30
0,95
40
0,92
50
0,89
60
0,86
70
0,81
80
0,75
Сравниваем 3 и 3 ;
90
0,69
100
0,60
0,66 0,65.
110
0,52
120
0,45
130
0,40
140
0,36
150
0,32
1
0,62 0,69
λ3 93
Из таблицы находим
0,69 0,60
3 0,69
3 0,66
10

35.

Проверим выполнение условия устойчивости:
σy R y
F
420кн
кн
σу
13,6 2 136МПа
2
A 3 30,8см
см
R y 3 R 0,66 210МПа 139МПа
Δ%
R y σy
Ry
139 136
100%
100% 2,2%
139
Недонапряжение составляет 2,2%. Это меньше 5%, что допустимо.
Окончательно принимаем d=7,82см.

36.

>
. Определим величину критической силы.
Материал стержня – сталь Ст3, для нее λпред=100. Так как
λ 3 93 λпред 100,
Из (12.14)
то выбираем формулу Ясинского.
Fкр A 3(a bλ3 );
Из справочника находим
a 31кн 2 ; b 0,114 кн 2
см
см
Fкр A 3(a bλ3 ) 30,8 (31
0,114 93) 628кн
≤
. Определим величину коэффициента запаса
устойчивости:
Fкр
628кн
ky
1,5
F
420кн