Similar presentations:
Устойчивость сжатых стержней. Лекция №13
1.
ЛЕКЦИЯ №131
УСТОЙЧИВОСТЬ СЖАТЫХ
СТЕРЖНЕЙ
2.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ2
В конструкциях и сооружениях большое применение находят детали, у
которых один или два размера поперечного сечения малы по сравнению с их
длиной.
При проведении расчетов
на прочность для таких
относительно
тонких
и
длинных стержней нельзя
основываться
только
на
условиях
прочности
при
растяжении-сжатии, так как их
поведение
под
действием
осевой сжимающей нагрузки
оказывается
принципиально
иным,
чем
при
сжатии
коротких стержней.
http://yourweatherblog.com/
3.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ3
Так, разрушение стержня при достижении сжимающей силой некоторой
критической величины может произойти не только потому, что будет
нарушена прочность, но и оттого, что стержень не сохранит формы,
приданной ему конструктором.
Прямолинейная форма равновесия окажется неустойчивой, и при
увеличении сжимающей силы стержень начнет интенсивно искривляться,
что вызовет появление изгибающих моментов от сжимающей силы и, стало
быть, добавочные напряжения от изгиба. При этом новым равновесным
состоянием упругого длинного стержня станет некоторая новая уже
криволинейная форма, а характер напряженного состояния в стержне
изменится. Это явление носит название потери устойчивости.
Устойчивость – способность тела сохранять положение или форму
равновесия при внешних воздействиях.
4.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ4
Центрально приложенная сжимающая сила, превышение которой
вызывает потерю устойчивости первоначальной формы равновесия тела,
называется критической силой.
Так, для надежной работы конструкции мало того, чтобы она была
прочна; надо, чтобы все ее элементы были устойчивы: они должны при
действии нагрузок деформироваться в таких пределах, чтобы характер их
работы оставался неизменным.
5.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ5
Формы равновесия
При
отклонении
от
положения
равновесия
система
Устойчивая
возвращается
в
форма
первоначальное
равновесия
положение, как только
причина, вызывающая
это
отклонение,
устранена.
Новое
положение
системы
после
Безразличная
отклонения
от
(критическая)
исходного
остается
форма
положением
равновесия
равновесия
и
после
удаления
внешнего воздействия.
Не возвращается
в
исходное
положение
Неустойчивая
равновесия
форма после
устранения
причины,
равновесия
а отклоняется от него
еще больше.
6.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ6
Р < Ркр
Q
При
удалении
поперечной
Устойчивая
Приложим
малую
нагрузки стержень
форма
поперечную
силу Q
будет
сохранять
равновесия
прямолинейную
форму равновесия
Р = Ркр
Q
Р > Ркр
Q
ДляПосле
выявления Даже
удаления
после
удаления
Равновесие
стержня
криволинейной
формы поперечной
Безразличная
поперечной
нагрузки
неустойчиво,
и нагрузки
любое
Неустойчивая
равновесия
приложим
к
(критическая)
стержень
сохраняет
стержень
продолжает
малое форма
возмущение
стержню
малую
новую форма
равновесную
искривляться
вызывает под действием
большие
равновесия
поперечную
возмущающую
криволинейную
всепрогибы.
возрастающих
при
равновесия
нагрузку
форму.Q, которая вызовет искривлении
изгибающих
малый прогиб.
моментов.
7.
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ7
Неустойчивая форма равновесия связана с неограниченным ростом
деформаций и напряжений, поэтому при превышении сжимающей силой её
критического значения конструкция разрушается.
Для обеспечения определенного запаса устойчивости необходимо
выполнение условия:
Р P
где:
P – сжимающая сила;
P
Pкр
– допускаемая нагрузка;
ny
Pкр – критическая сила;
n y – коэффициент запаса устойчивости.
Продольным изгибом называется изгиб стержня, вызванный потерей
устойчивости прямолинейной формы его равновесия. При потере
устойчивости прогиб произойдет перпендикулярно к оси наименьшей
жесткости стержня.
8.
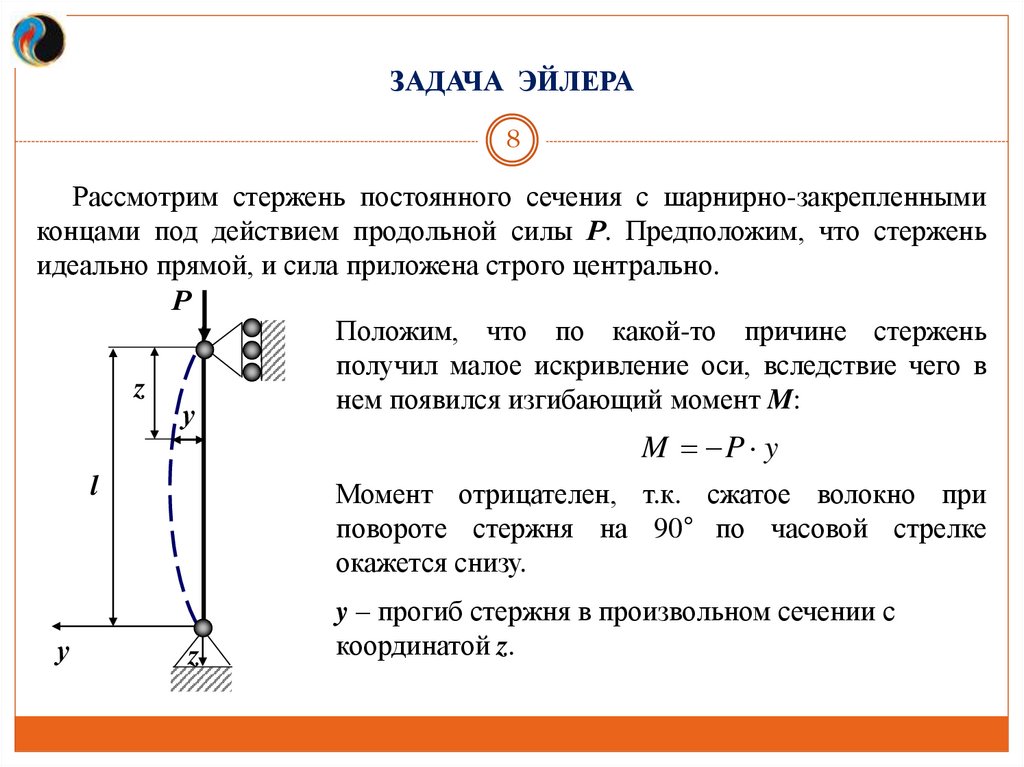
ЗАДАЧА ЭЙЛЕРА8
Рассмотрим стержень постоянного сечения с шарнирно-закрепленными
концами под действием продольной силы Р. Предположим, что стержень
идеально прямой, и сила приложена строго центрально.
Р
Положим, что по какой-то причине стержень
получил малое искривление оси, вследствие чего в
z
нем появился изгибающий момент M:
у
M P y
l
у
Момент отрицателен, т.к. сжатое волокно при
повороте стержня на 90° по часовой стрелке
окажется снизу.
z
y – прогиб стержня в произвольном сечении с
координатой z.
9.
ЗАДАЧА ЭЙЛЕРА9
Приближенное дифференциальное уравнение упругой линии для
стержня имеет вид:
d2y
M
dz 2 E J
d2y
P y
2
dz
E J
справедливо только при соблюдении закона Гука
Введем обозначение:
P
k
E J
2
d2y 2
k y 0
тогда:
2
dz
Решение уравнения имеет вид:
y ( z ) A sin kz B cos kz
Уравнение имеет три неизвестные (постоянные интегрирования А, В и
параметр k).
10.
ЗАДАЧА ЭЙЛЕРА10
Найдем неизвестные из граничных условий закрепления стержня по
концам:
Р
1)
y (0) 0
y (0) 0 , т.е. 0 A sin k 0 B cos k 0
0 B cos k 0 , значит, B 0
Значит, уравнение имеет вид
y ( z ) A sin kz
уmax
l
При продольном изгибе изогнутая ось стержня может быть
представлена как некоторое число волн синусоиды с амплитудой А.
2)
y (l ) 0, т.е. 0 B sin kl
у
Если А=0 и В=0, то y ( z ) 0 , что не соответствует условию задачи
Следовательно, sin kl 0
y (l ) 0
z
11.
ЗАДАЧА ЭЙЛЕРА11
Из свойств синусоиды следует, что k
n
l
n– произвольное целое число полуволн синусоиды, укладывающихся на
длине изогнутой оси стержня ( n 1, 2, 3... , т.к. при n = 0 k = 0 и Р = 0)
P
E J
Р1
Р2
Р3
P
n
E J
l
n=1
n=2
n=3
k
P
2 n2 E J
l2
Так, получено выражение для некоторых фиксированных значений
сжимающей силы, при которых возможна криволинейная форма
равновесия оси стержня.
12.
ЗАДАЧА ЭЙЛЕРА12
Сжимающая сила принимает минимальное значение при:
1) Минимальном n (n = 1): на длине стержня укладывается одна полуволна
синусоиды (при отсутствии дополнительных укреплений)
2) Минимальном J (J = Jmin): стержень искривляется относительно оси с
наименьшим моментом инерции
Итак, минимальное значение сжимающей силы, после которого происходит
потеря устойчивости стержня, определяется выражением:
P
2 E J min
l
2
формула Эйлера
Критическая сила (сила Эйлера)
13.
ЗАДАЧА ЭЙЛЕРА13
Пример:
P
y
x
P
а
2 E J min
l2
3
2a a 3 a 4
Jy
12
6
y
x
2а
поперечное сечение стержня
z
a 2a 4a 4
Jx
12
6
J y J min
Прогиб
произойдет
перпендикулярно оси y
При выборе сечения стержней, работающих на
устойчивость, следует отдавать предпочтение таким,
которые
обеспечивают
равноустойчивость
(одинаковую гибкость относительно обеих главных
осей), то есть с одинаковыми главными осевыми
моментами инерции.
14.
ЗАДАЧА ЭЙЛЕРА14
J i2 F
i – радиус инерции сечения
Для получения наиболее устойчивых стержней следует выбирать формы
сечения с наибольшими радиусами инерции при данной площади:
Кроме того, из формулы Эйлера видно, что из всех механических
характеристик материала играет роль лишь модуль Юнга, так что
критическая сила не зависит от прочностных свойств материала, т.е. стержни
одинаковой длины (l) и геометрии сечения (Jmin), изготовленные из
различных материалов, при одинаковых условиях закрепления изогнутся при
одном и том же значении силы Р.
15.
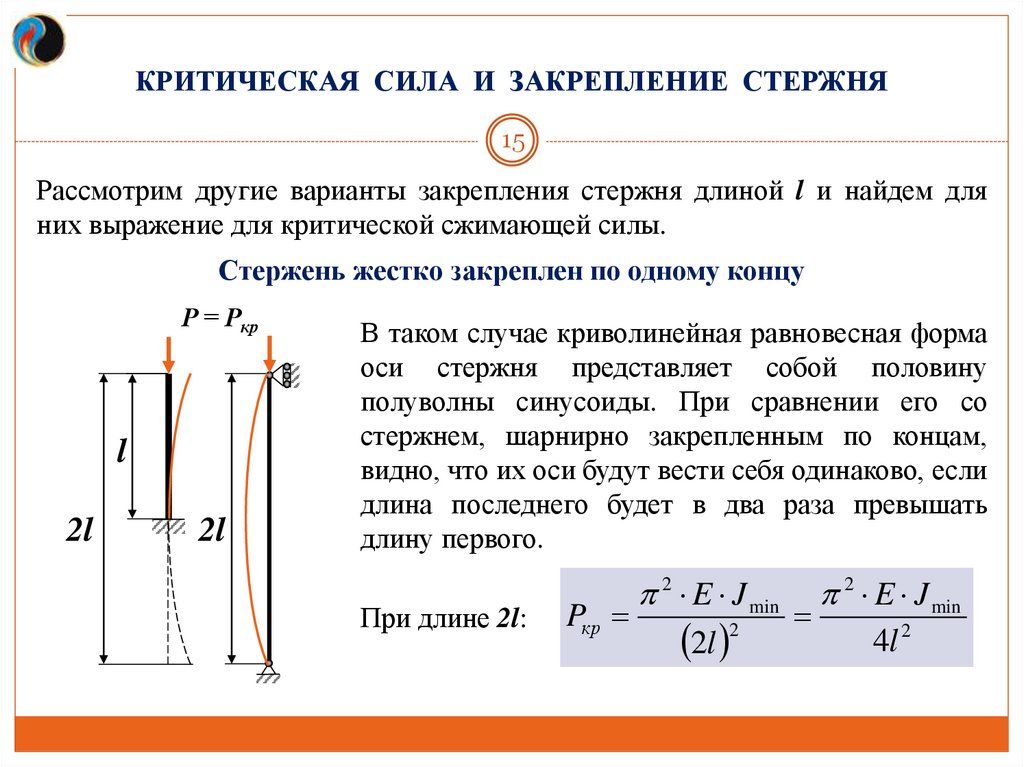
КРИТИЧЕСКАЯ СИЛА И ЗАКРЕПЛЕНИЕ СТЕРЖНЯ15
Рассмотрим другие варианты закрепления стержня длиной l и найдем для
них выражение для критической сжимающей силы.
Стержень жестко закреплен по одному концу
Р = Ркр
l
2l
2l
В таком случае криволинейная равновесная форма
оси стержня представляет собой половину
полуволны синусоиды. При сравнении его со
стержнем, шарнирно закрепленным по концам,
видно, что их оси будут вести себя одинаково, если
длина последнего будет в два раза превышать
длину первого.
При длине 2l:
Pкр
2 E J min
2l
2
2 E J min
4l 2
16.
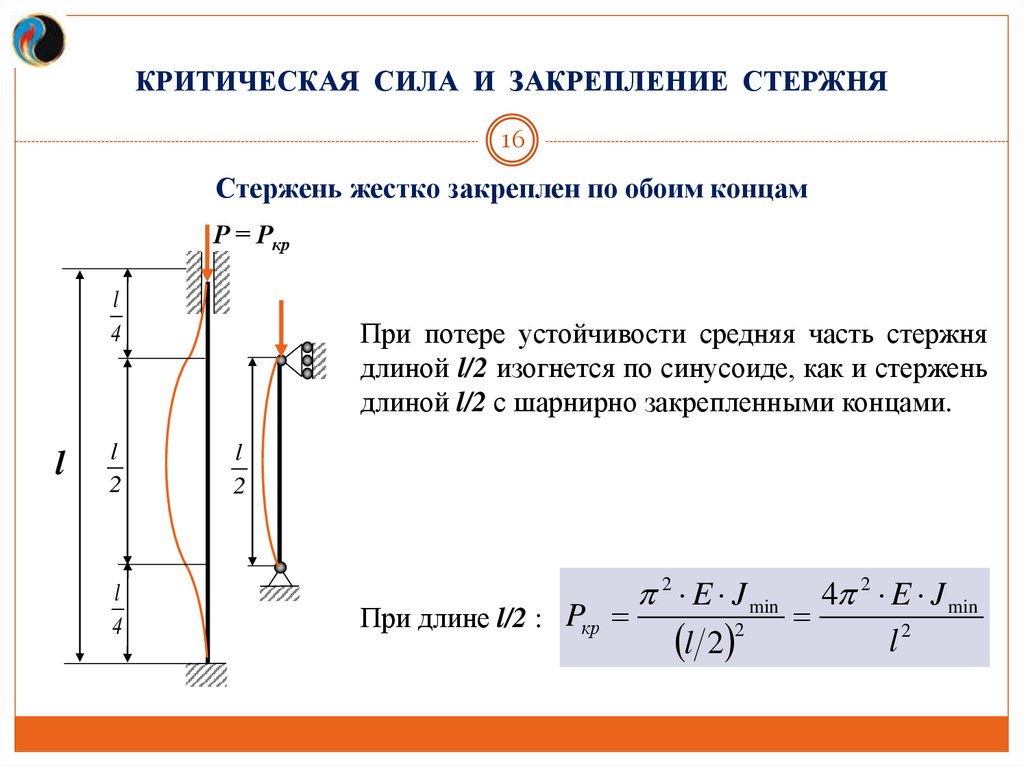
КРИТИЧЕСКАЯ СИЛА И ЗАКРЕПЛЕНИЕ СТЕРЖНЯ16
Стержень жестко закреплен по обоим концам
Р = Ркр
l
4
l
l
2
l
4
При потере устойчивости средняя часть стержня
длиной l/2 изогнется по синусоиде, как и стержень
длиной l/2 с шарнирно закрепленными концами.
l
2
При длине l/2 : Pкр
2 E J min
l 2 2
4 2 E J min
l2
17.
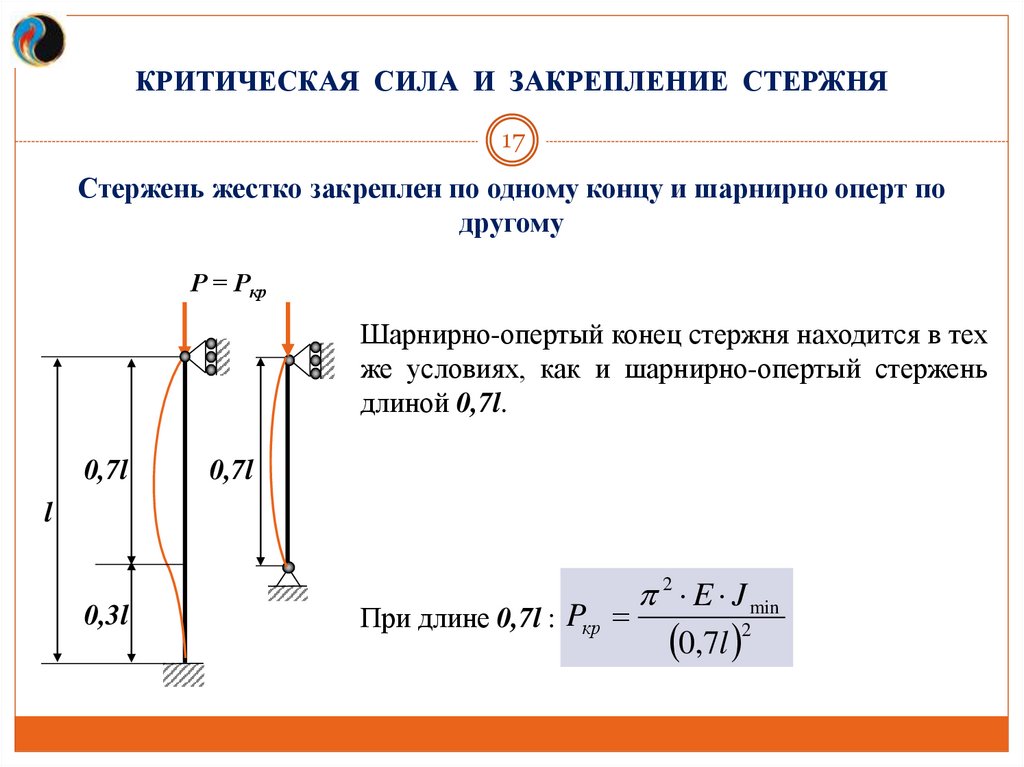
КРИТИЧЕСКАЯ СИЛА И ЗАКРЕПЛЕНИЕ СТЕРЖНЯ17
Стержень жестко закреплен по одному концу и шарнирно оперт по
другому
Р = Ркр
Шарнирно-опертый конец стержня находится в тех
же условиях, как и шарнирно-опертый стержень
длиной 0,7l.
0,7l
0,7l
l
0,3l
При длине 0,7l : Pкр
2 E J min
0,7l 2
18.
КРИТИЧЕСКАЯ СИЛА И ЗАКРЕПЛЕНИЕ СТЕРЖНЯ18
Итак, сопоставив формулы для определения критической силы Ркр,
получаем:
2 E J min
Pкр
l 2
где:
или:
Pкр
2 E J min
l
2
пр
μ – коэффициент приведения длины
l – фактическая длина стержня
lпр – приведенная длина стержня lпр l
Коэффициент приведения длины μ
показывает, чему равна длина одной
полуволны синусоиды при заданной длине
стержня.
μ
1
0,5
0,5
0,7
19.
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ19
По значению критической силы Ркр можно определить соответствующее
ей сжимающее напряжение кр, при котором стержень теряет устойчивость:
2 E J min
кр
F
l 2
Pкр
Критическое
напряжение
что можно выразить через минимальный радиус инерции сечения imin
Обозначим:
l
imin
2
2 E imin
кр
l 2
J min
F
– гибкость стержня (безразмерная величина). Тогда:
2 E
кр 2
20.
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ20
Опять же, из всех механических характеристик материала на
критическое напряжение влияет только модуль Юнга. Для одного материала
зависимость между кр и λ может быть представлена гиперболической
кривой, называемой гиперболой Эйлера.
Так как при выведении формулы Эйлера было допущено, что
деформация проходит с соблюдением закона Гука, то и использовать её
можно только пока критическое напряжение кр не превысило значения
предела пропорциональности пц по диаграмме сжатия материала:
2 E
при кр
пц
2
гипербола
Эйлера
λ
в
р
т
пц
О
А
диаграмма
сжатия
материала
ε
21.
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ21
Тогда определим предельную гибкость:
2E
пр
пц
предельная гибкость, при которой
применима формула Эйлера
Формула Эйлера применима для сжатого стержня лишь при условии, что его
расчетная гибкость не менее (больше или равна) предельной гибкости:
расч пр
Например, для малоуглеродистых сталей
2E
2 2 105
пр
100
пц
200
Предельная гибкость стержня не зависит от формы его сечения, а только от
механических прочностных и деформационных свойств материала (предел
прочности и модуль Юнга, соответственно).
22.
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ22
При пр формула Эйлера становится неприемлемой и дает
завышенные значения критической силы и критического напряжения, то есть
переоценивает действительную устойчивость стержней.
l
50,
Пример: расчетная гибкость стального стержня расч
imin
т.е. расч пр , но критическое напряжение
2 Е 3,142 2 1011
кр 2
788,8МПа , т.е. кр пц .
2
50
(для Ст3 σпц = 195-200МПа)
Применение формулы Эйлера в этом случае опасно!
Теоретическое
решение
задачи
об
устойчивости
за
пределом
пропорциональности сложно, поэтому для расчетов на устойчивость в этой области
обычно пользуются эмпирическими формулами, полученными в результате обработки
большого числа экспериментальных данных.
23.
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ23
При расчетах стержней средней
используется формула Ясинского
гибкости
((0,3-0,4) пр˂ пр)
кр а b
где a и b – коэффициенты, зависящие от свойств материала и определяемые
экспериментально.
Пример:
cталь 40 характеризуется коэффициентами а = 321 МПа, b = 1,16 МПа
сталь Ст3 – а = 310 МПа, b = 1,14 МПа
Стержни с малой гибкостью ( (0,3-0,4) пр, например, стальные)
будут при разрушении раньше терять прочность, чем устойчивость. Для
таких стержней проводят обычный расчет на прочность, принимая в
качестве предельного напряжения предел текучести т для пластичных
материалов или предел прочности в для хрупких материалов.
24.
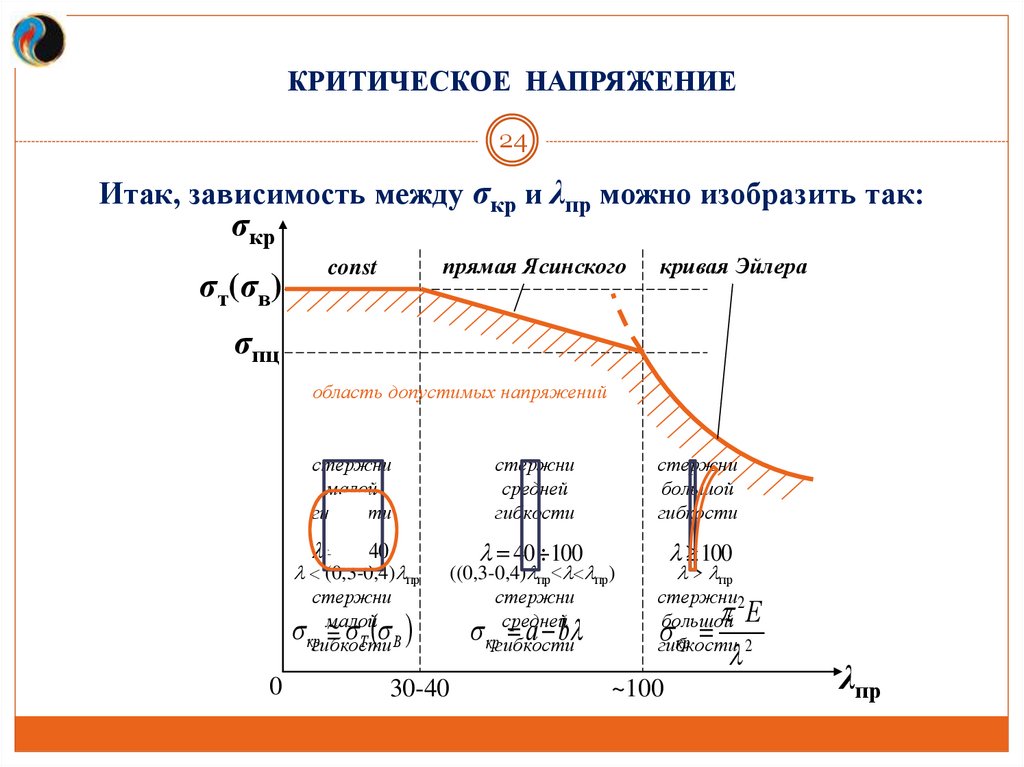
КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ24
Итак, зависимость между σкр и λпр можно изобразить так:
σкр
σт(σв)
прямая Ясинского
const
кривая Эйлера
σпц
область допустимых напряжений
стержни
малой
гибкости
0 40
(0,3-0,4) пр
стержни
малой
кргибкости
Т В
0
стержни
средней
гибкости
стержни
большой
гибкости
40 100
100
стержни2
Е
большой
гибкости
кр
2
((0,3-0,4) пр˂ пр)
стержни
средней
а b
кргибкости
30-40
~100
> пр
λпр
25.
ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙДЛЯ СЖАТЫХ СТЕРЖНЕЙ
25
Итак, при проектировании стержней, подвергающихся сжатию,
необходимо проводить две проверки: на прочность и на устойчивость.
Стержни малой гибкости рассчитывают на прочность. Стержни большой
и средней гибкости рассчитывают на прочность и устойчивость.
а) проверка на прочность
P
F
В
Т
где
для пластичных материалов и
для хрупких материалов
nВ
nT
а) проверка на устойчивость
max
P
у
F
кр
где у
– допускаемое напряжение при расчете на устойчивость
nу
n у – коэффициент запаса устойчивости
max
26.
ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙДЛЯ СЖАТЫХ СТЕРЖНЕЙ
26
Коэффициент запаса устойчивости ny стержня зависит от его гибкости и
материала, из которого он изготовлен. Коэффициент запаса устойчивости
всегда выше коэффициента запаса на прочность, так как на устойчивости
сказываются многие факторы, которые незначительно снижают прочность
стержня (начальная кривизна стержня, эксцентриситет приложения
нагрузки, неоднородность материала и т.п.)
Пример: для сталей ny как правило лежит в пределах от 1,8 до 3, тогда как nпр – от 1,4
до 1,6.
Сравнивая выражения для допускаемых напряжений на устойчивость и
прочность, установим связь между этими напряжениями:
кр nпр
у n
у
пр
обозначим в общем случае σТ
и σВ как σпр, а nТ и nВ как nпр
27.
ОПРЕДЕЛЕНИЕ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙДЛЯ СЖАТЫХ СТЕРЖНЕЙ
27
Введем φ – коэффициент продольного изгиба (коэффициент
уменьшения основного допускаемого напряжения при расчете на
устойчивость):
кр nпр
n у пр
φ – справочная величина, зависящая от материала стержня и его гибкости.
Тогда условие устойчивости примет вид:
P
max
F
Пример: для стали Ст3
λ
φ
120
100
80
60
→0
0,45
0,6
0,75
0,86
→1
28.
РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ28
Для сжатых стержней проводят как проверочные, так и проектировочные
расчеты на прочность:
а) проверочный расчет проводится по такой схеме:
1. Вычисляется гибкость стержня λ исходя из известных размеров,
формы и условий закрепления:
l
imin
2. По справочной таблице для известного материала и гибкости
находится коэффициент продольного изгиба φ и допускаемое
напряжение на устойчивость:
кр nпр
кр nпр
у
n у пр
n у пр
P
3. Проверяется соблюдение условия устойчивости max у
F
29.
РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ29
б) проектировочный расчет по подбору сечения под заданную нагрузку
проводится методом последовательных приближений, так как в условии
устойчивости участвуют две неизвестных величины – искомая площадь
поперечного сечения F и коэффициент продольного изгиба φ, зависящий
от гибкости стержня, а значит, и от неизвестной площади F:
1. Коэффициент продольного изгиба φ принимается за φ1=0,5÷0,6,
вычисляется площадь F в первом приближении:
F
2.
3.
P
1
По найденной площади F подбирается сечение и вычисляется
гибкость стержня в первом приближении λ1. По λ1 по справочной
таблице находится новое значение φ1’.
Проверяется соблюдение условия устойчивости исходя из найденного
φ1’, и если σmax заметно (> чем на 5%) отличается от [σу], то расчет
повторяется с φ1=(φ1+ φ1’)/2.
























 mechanics
mechanics








