Similar presentations:
Основы классической механики. Электростатика. Постоянный ток
1.
Тема: «Основы классическоймеханики. Электростатика.
Постоянный ток
Ус т а н о в о ч н а я с е с с и я
К р а в цо в а Н а т а л ь я А н а тол ь е в н а
к . ф и з - м а т. н . , до це н т ка ф . « Ф и з и ка и
т е о р е т и ч е с ка я м ех а н и ка »
2.
ЛИТЕРАТУРА1.Трофимова Т.И. Курс физики. –
М.: Высшая школа, 2001 (2002,
2003 и т.д.)
2.Детлаф А .А ., Яворский Б.М.,
Милковская Л.Б. Курс физики. –
М.: Высшая школа, 2001 (2002,
2003 и т.д.)
3.Трофимова Т.И., Павлова З.Г.
Сборник задач по курсу физики с
решениями. – М.: Высшая школа,
2003.
3.
4.Чертов А.Г., Воробьёв А .А .Задачник по физике. – М.: Высшая
школа, 2009.
5.Фирганг Е.В. Руководство к
решению задач по курсу общей
физики. – М.: Высшая школа, 2009
4.
1 0 1 – 1 1 0 . О с н о в ы к и н ем а т и к ип о с т у п а т ел ь н о го и в р а щ а т ел ь н о го д в и же н и й
М АТ Е Р И А Л Ь Н А Я Т О Ч К А - э т о т е л о , р а з м е р ы ,
форма и внутренняя структура которого в
данной задаче несущественны
А Б С ОЛ Ю Т Н О Т В Е РД О Е Т Е Л О - т е л о ,
деформациями которого в условиях данной
задачи можно пренебречь
С И С Т Е М А ОТС Ч Е ТА
Т Е Л О О ТС Ч Е ТА
С И С Т Е М А КО О РД И Н АТ
П Р И Б О Р Д Л Я О П Р Е Д Е Л Е Н И Я В Р Е М Е Н И
5.
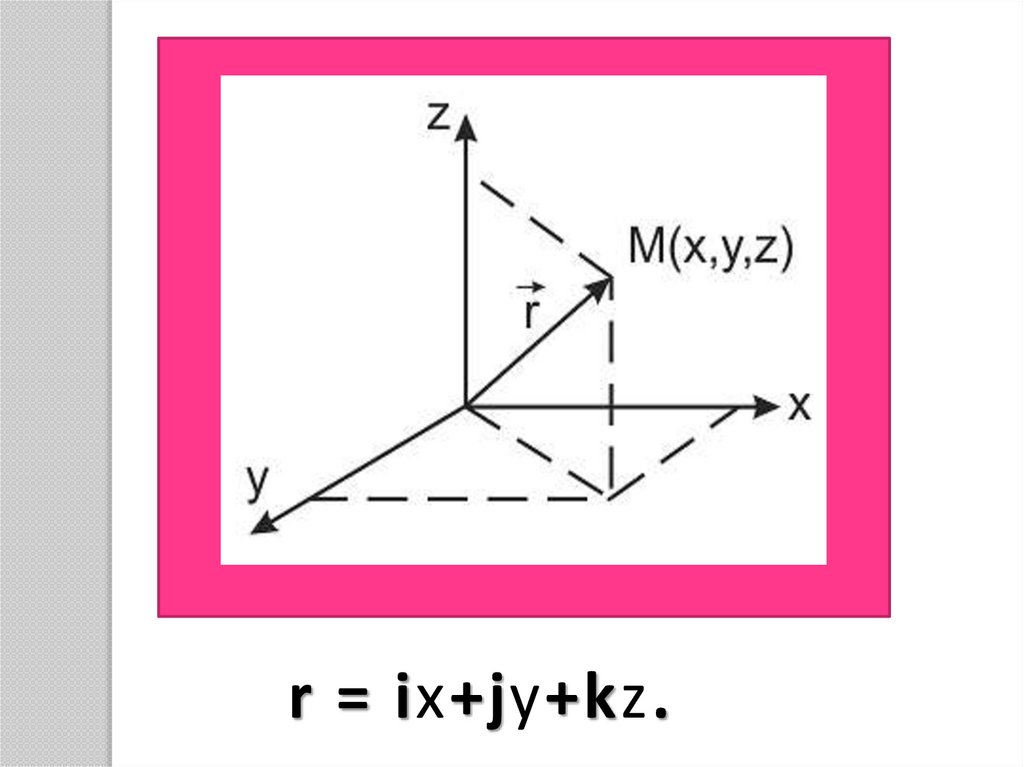
r = ix+jy+kz.6.
zÎ
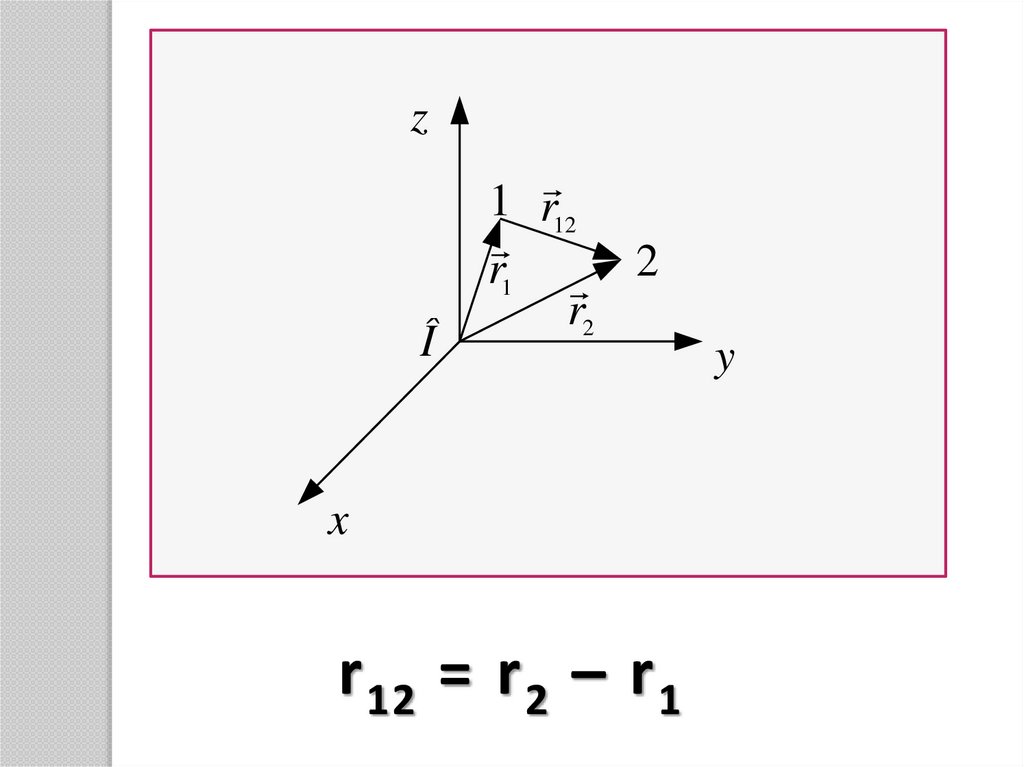
1 r12
r1 2
r2
x
r 12 = r 2 – r 1
y
7.
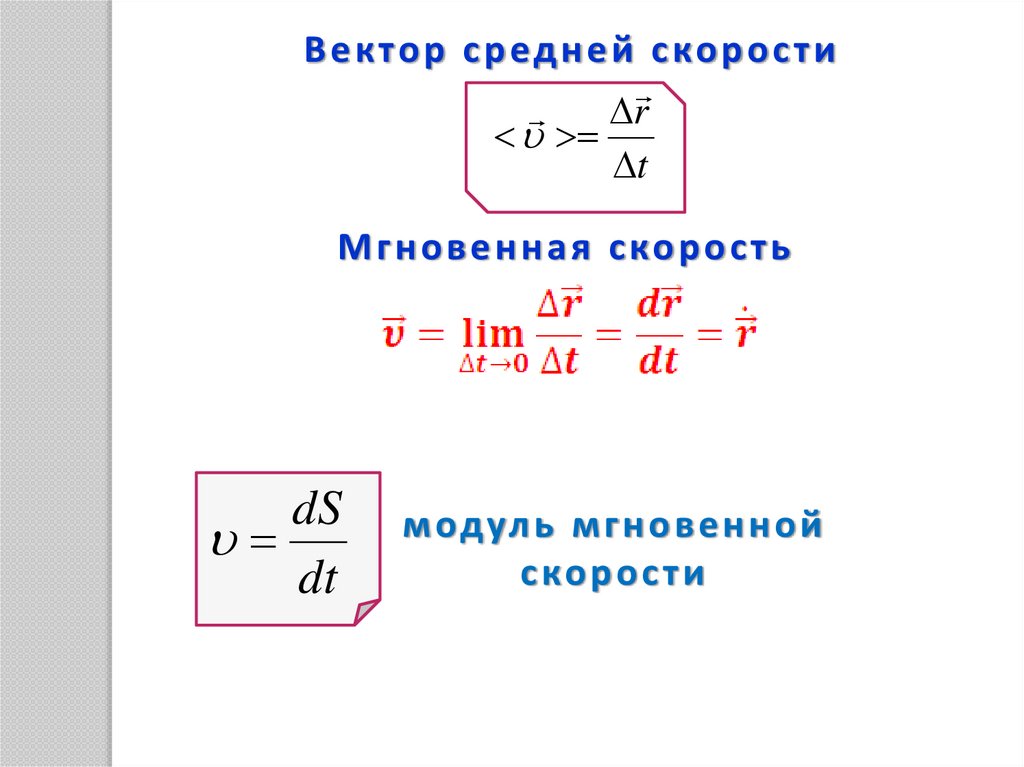
В е к то р с р ед н е й с ко р о с т иr
t
М г н о в е н н а я с ко р о с т ь
dS
dt
м одул ь м г н о в е н н о й
с ко р о с т и
8.
КО М П О Н Е Н Т Ы В Е КТО РА С КО Р О С Т Иi x j y k z
r i x j y kz
x x , y y , z z
9.
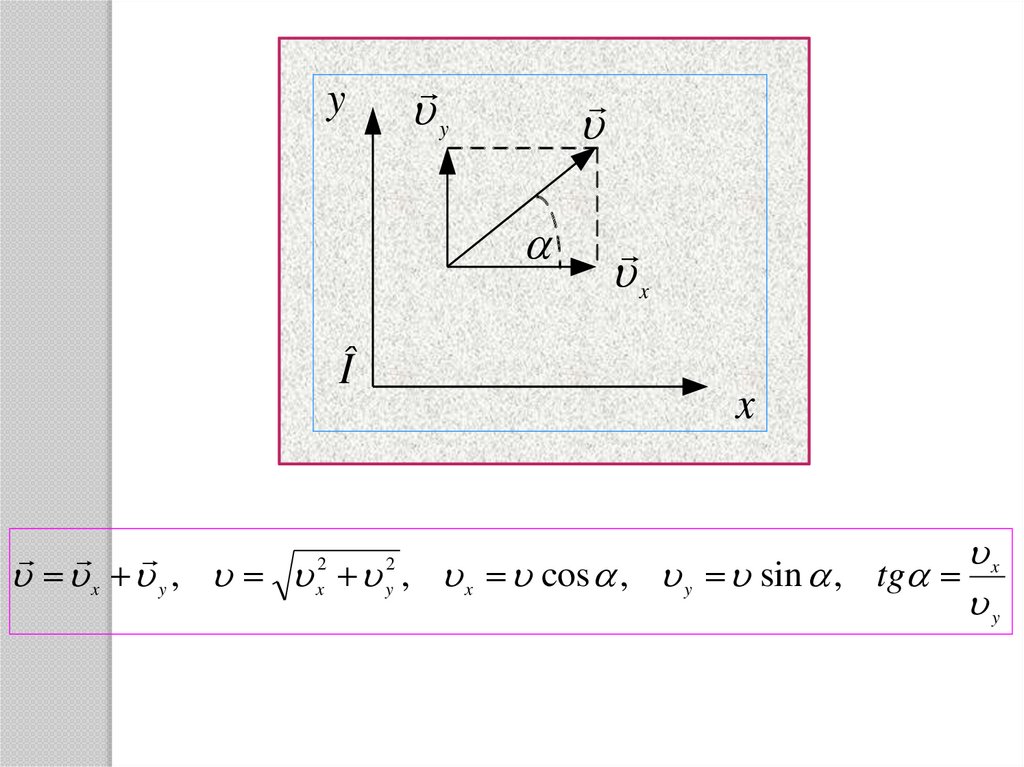
yy
Î
x
x
x
x y , , x cos , y sin , tg
y
2
x
2
y
10.
СРЕДНЯЯ ПУТЕВАЯ СКОРОСТЬS
t
СРЕДНЕЕ УСКОРЕНИЕ
a
t
МГНОВЕННОЕ УСКОРЕНИЕ
d d r
a im
2 r
t 0
t
dt
dt
2
11.
ana
a
a a an
d
a
dt
an
2
r
a a a
2
2
n
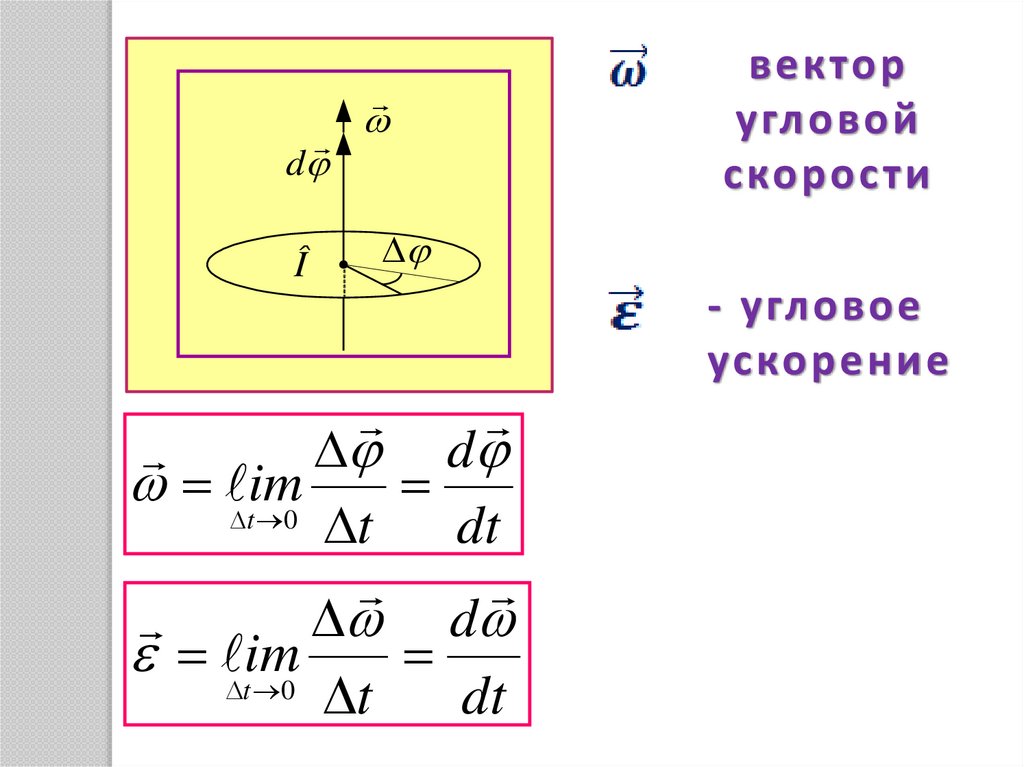
12.
векторугловой
скорости
d
Î
- угловое
ускорение
d
tim
0
t
dt
d
tim
0
t
dt
13.
ra r
a r
an
an r
r
2
14.
1 1 1 – 1 2 0 . И м п ул ь с . З а ко н с ох р а н е н и яи м п ул ь с а
и м п ул ь с т ел а
F 0
dP
0
dt
P const
с ум м а р н ы й и м п ул ь с з а м к н у то й
с и с т ем ы ч а с т и ц о с т а е тс я п о с то я н н ы м
15.
16.
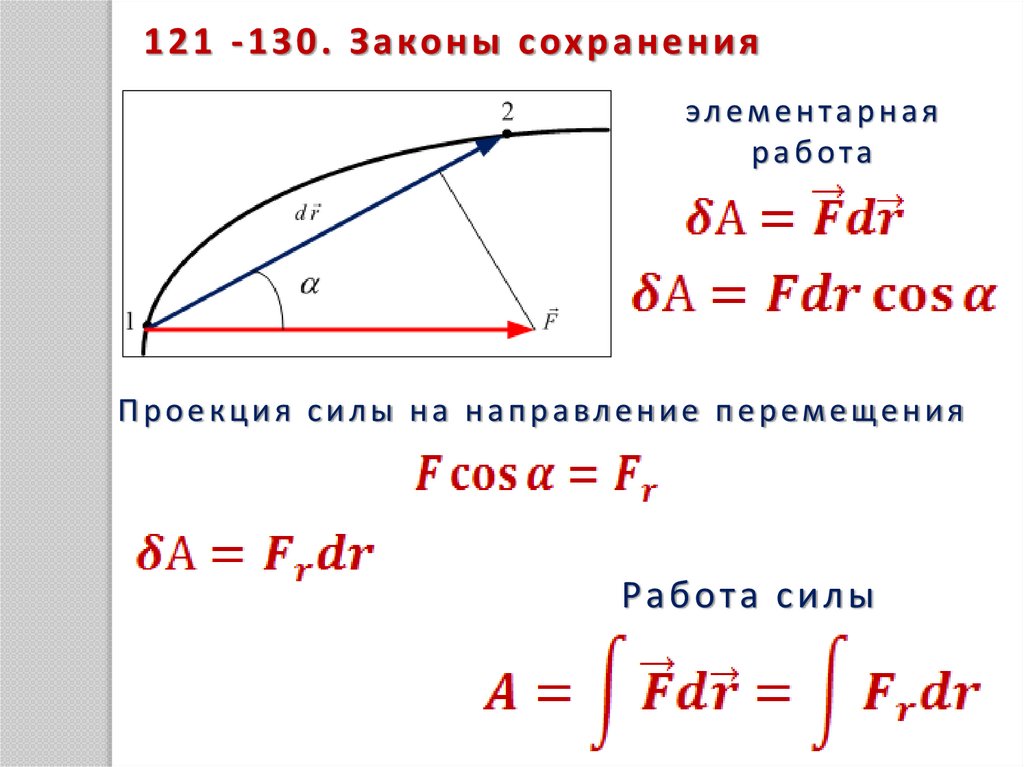
1 2 1 - 1 3 0 . З а ко н ы с ох р а н е н и яэлементарная
работа
Проекция силы на направление перемещения
Р а б от а с и л ы
17.
кинетическаяэнергия
потенциальная
энергия
деформированного
тела
потенциальная
энергия тела,
поднятого над
Землей
18.
полнаямеханическая
энергия
ЗА КО Н С ОХ РА Н Е Н И Я М Е Х А Н И Ч ЕС КО Й
ЭНЕРГИИ
Ес л и н а т ел о де й с т ву ют тол ь ко
ко н с е р в а т и в н ы е с и л ы , п ол н а я э н е р г и я
с и с т ем ы с ох р а н я е тс я
19.
Р а б от а с и л ы у п ру го с т и . Р а б о т а с и л ыт я же с т и
з а к о н Гу к а
РА Б О ТА С И Л Ы У П Р У Г О С Т И
РА Б О ТА С И Л Ы Т Я Ж Е С Т И
20.
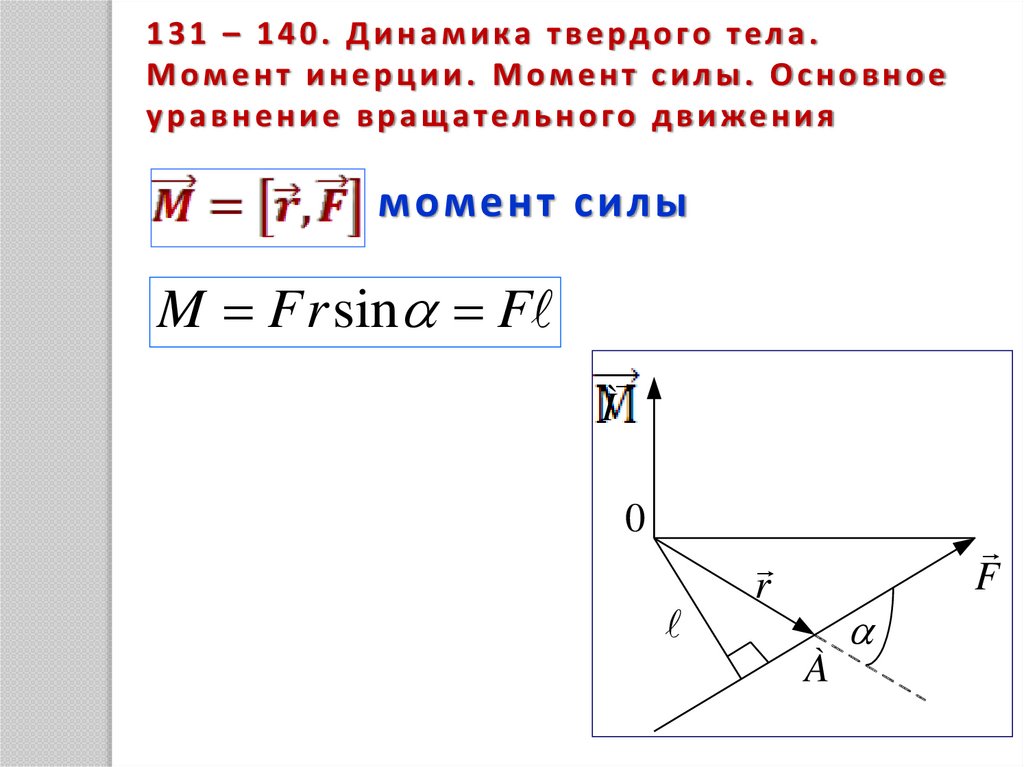
131 – 140. Динамика твердого тела.Момент инерции. Момент силы. Основное
уравнение вращательного движения
момент силы
M F r sin F
Ì
0
F
r
À
21.
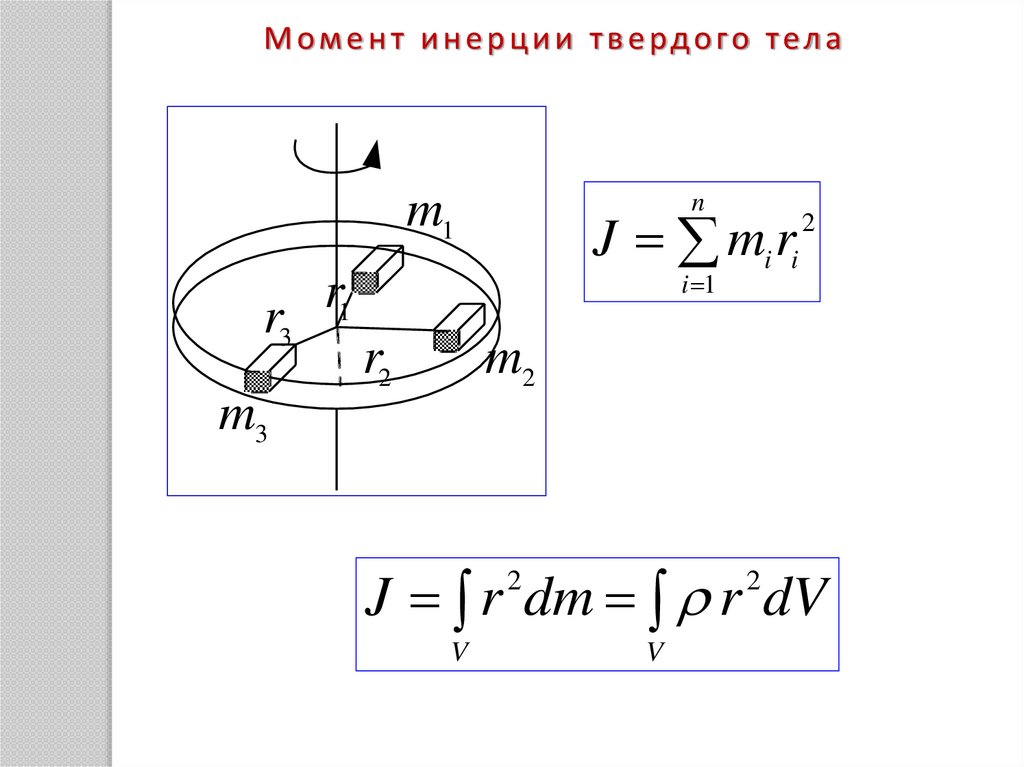
М о м е н т и н е р ц и и т в е рд о г о т е л аm1
r
r3 1
n
J mi ri
2
i 1
r2
m2
m3
J r dm r dV
2
V
2
V
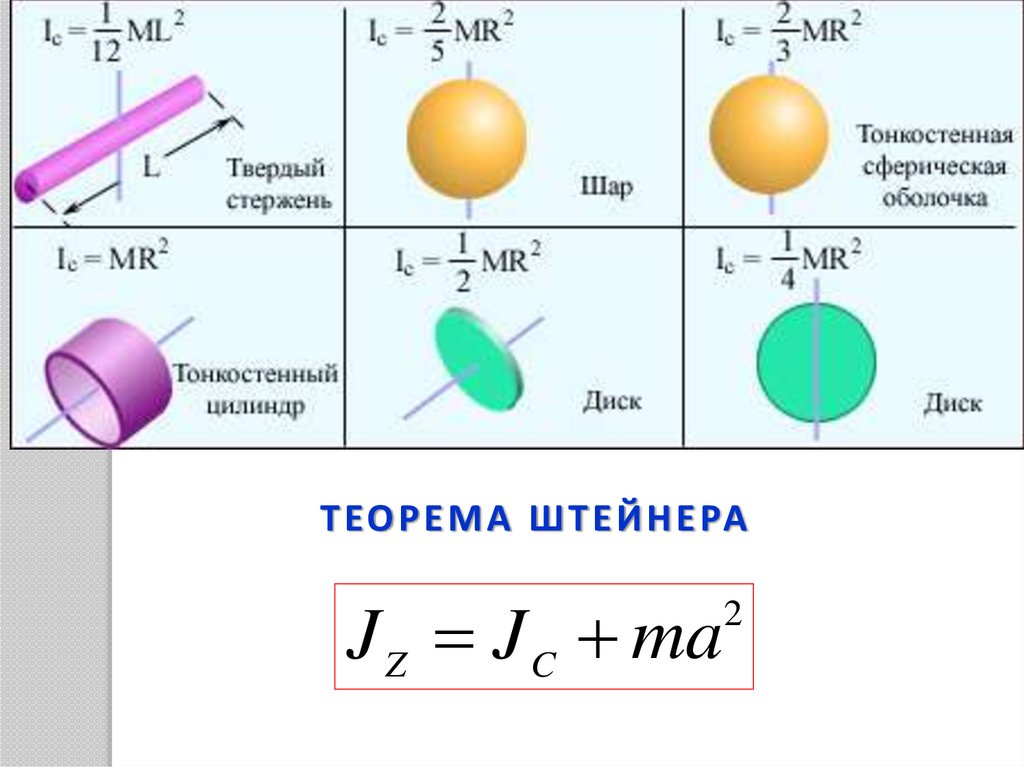
22.
Т ЕО Р Е М А Ш Т Е Й Н Е РАJ Z J C ma
2
23.
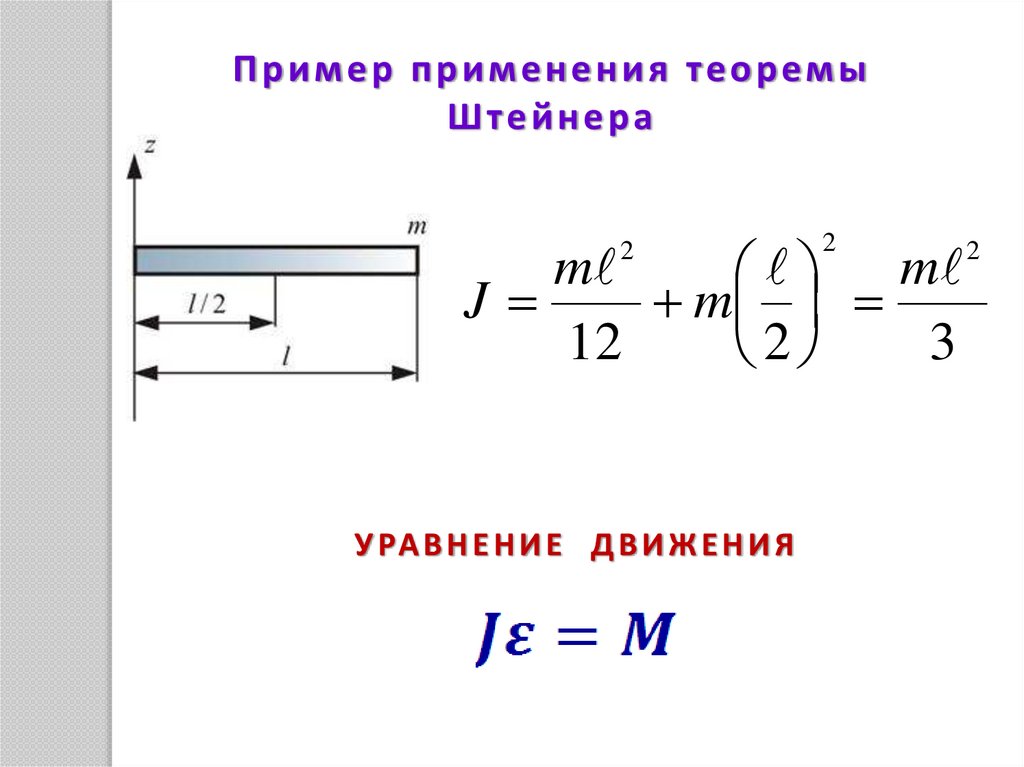
П р и м е р п р и м е н е н и я т е о р ем ыШтейнера
2
m
m
J
m
12
3
2
2
У РА В Н Е Н И Е Д В И Ж Е Н И Я
2
24.
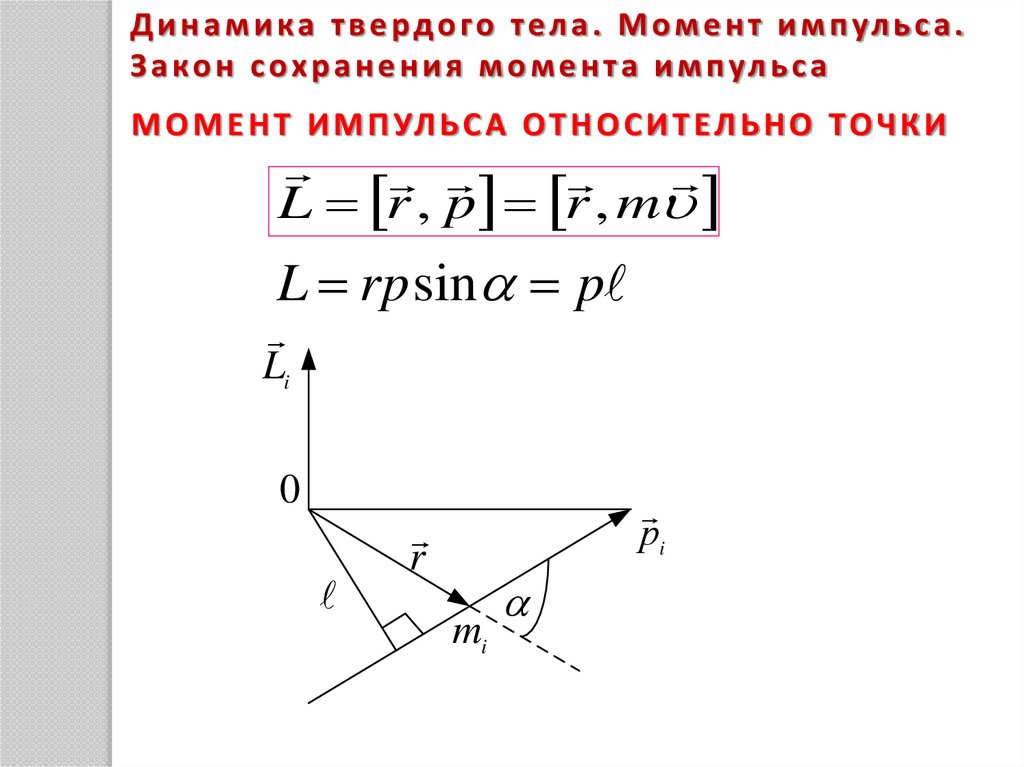
Д и н а м и к а т в е р д о г о т е л а . М о м е н т и м п ул ь с а .З а к о н с о х р а н е н и я м о м е н т а и м п ул ь с а
М О М Е Н Т И М П УЛ Ь С А О Т Н О С И Т Е Л Ь Н О Т О Ч К И
L r , p r , m
L rp sin p
Li
0
рi
r
mi
25.
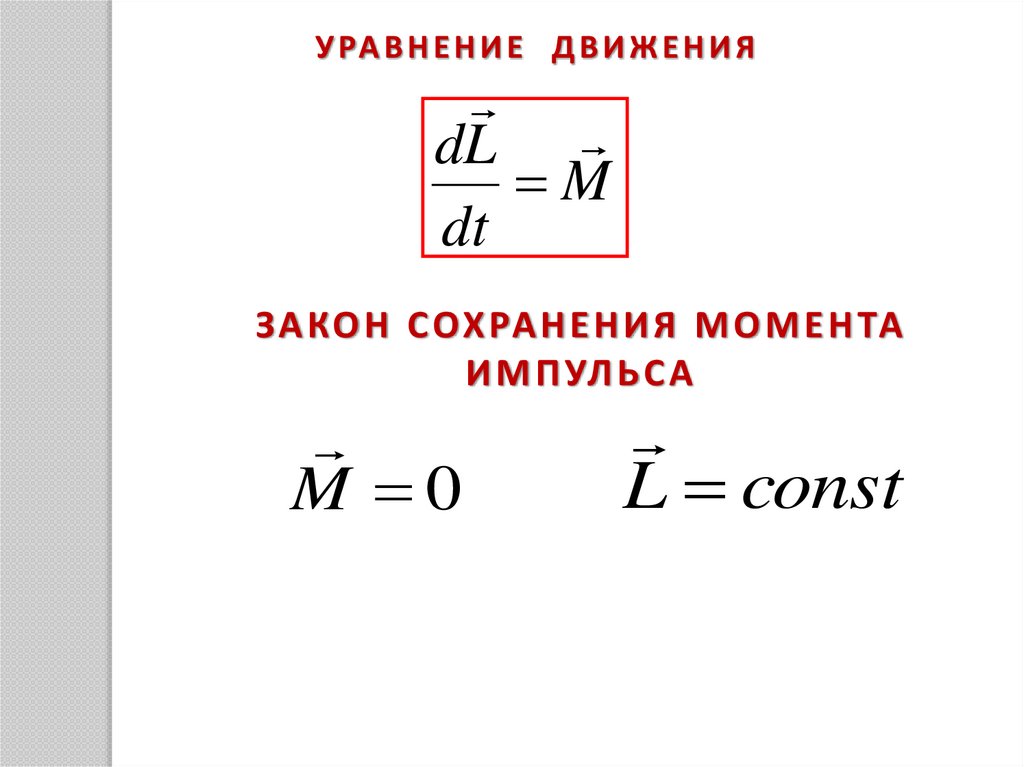
У РА В Н Е Н И Е Д В И Ж Е Н И ЯdL
M
dt
ЗА КО Н С ОХ РА Н Е Н И Я М О М Е Н ТА
И М П УЛ Ь С А
M 0
L const
26.
J M zd
J
Mz
dt
27.
1 4 1 - 1 5 0 З а к о н К ул о н а . Н а п р я ж е н н о с т ьэлектрического поля
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
Физическая величина, характеризующая
свойство тел или частиц вступать в
электромагнитные взаимодействия и
определяющая значения сил и энергий при
т а к и х в з а и м од е й с т в и я х
Э л е к т р и ч е с к и й з а р я д – фу н д а м е н т а л ь н о е
неотъемлемое свойство элемент арных частиц
П О Л О Ж И Т Е Л Ь Н Ы Е И О Т Р И Ц АТ Е Л Ь Н Ы Е
28.
НАИМЕНЬШАЯ ВЕЛИЧИНА ЗАРЯДАе =1,60219·10 -19 Кл
–
эл ем е н т а р н ы й з а р я д
П Р ОТО Н – эл ем е н т а р н а я ч а с т и ц а ,
в ход я щ а я в с о с т а в а то м а и и м е ю щ а я
заряд + е
ЭЛ Е КТ Р О Н – эл ем е н т а р н а я ч а с т и ц а ,
имеющая заряд – е
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД КВАНТ УЕТСЯ
( П Р И Н И М А Е Т О П Р Е Д Е Л Е Н Н Ы Е Д И С К Р Е Т Н Ы Е З Н АЧ Е Н И Я ) :
q = Ne ,
ГД Е
N
– ЦЕЛОЕ ЧИСЛО
29.
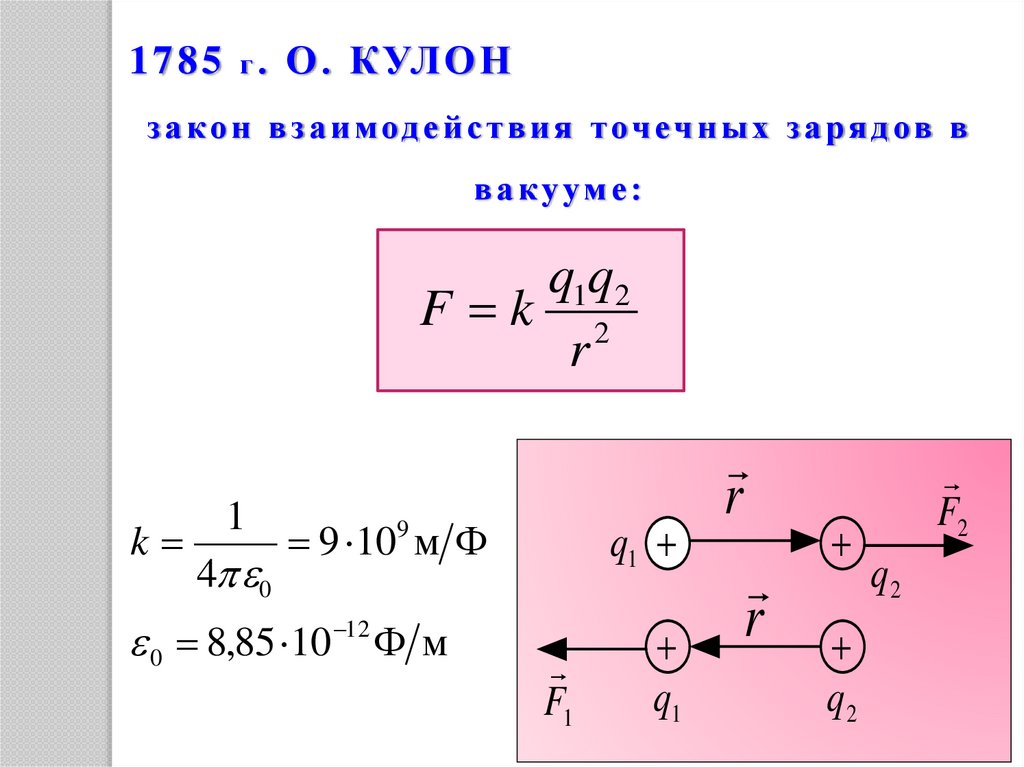
1 7 8 5 г . О . КУЛ О Нз а к о н в з а и м од е й с т в и я т оч еч н ы х з а р я д ов в
вакууме:
q1q2
F k 2
r
k
1
4 0
q1
9 109 м Ф
0 8,85 10 Ф м
12
F1
q1
r
r
q2
F2
q2
30.
ЭЛ Е К Т Р И Ч Е С КО Е П ОЛ Е –силовое поле, посредством которого
взаимодействуют электрические заряды
Э Л Е К Т Р О С ТАТ И Ч Е С К О Е П ОЛ Е –
п ол е , с о зд а в а ем о е н е п од в и ж н ы м и
зарядами
пробный точечный положительный
заряд –точечный заряд , не искажающий своим
присутствием самого поля
н ап р я же н н о с т ь Е
F
Е
Q0
напряженность поля
т оч еч н о го з а р я д а
q
Е k 2
r
31.
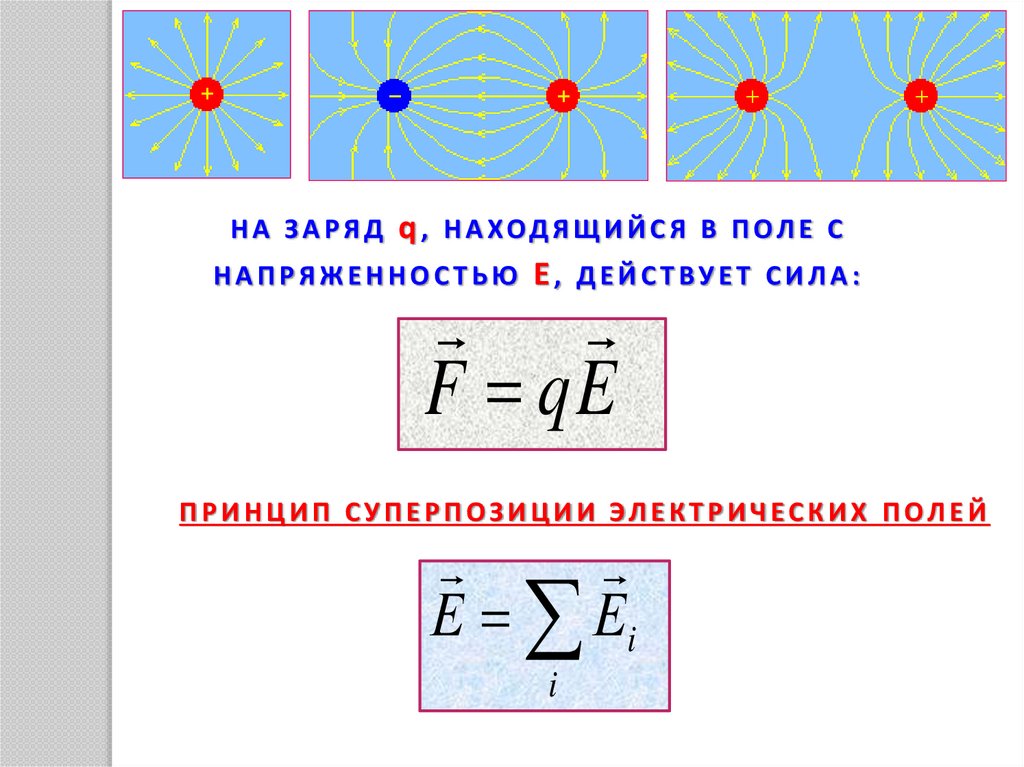
НА ЗАРЯД q, НАХОДЯЩИЙСЯ В ПОЛЕ СНАПРЯЖЕННОСТЬЮ Е, ДЕЙСТВУЕТ СИЛА:
F qE
ПРИНЦИП СУПЕРПОЗИЦИИ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ
Е Еi
i
32.
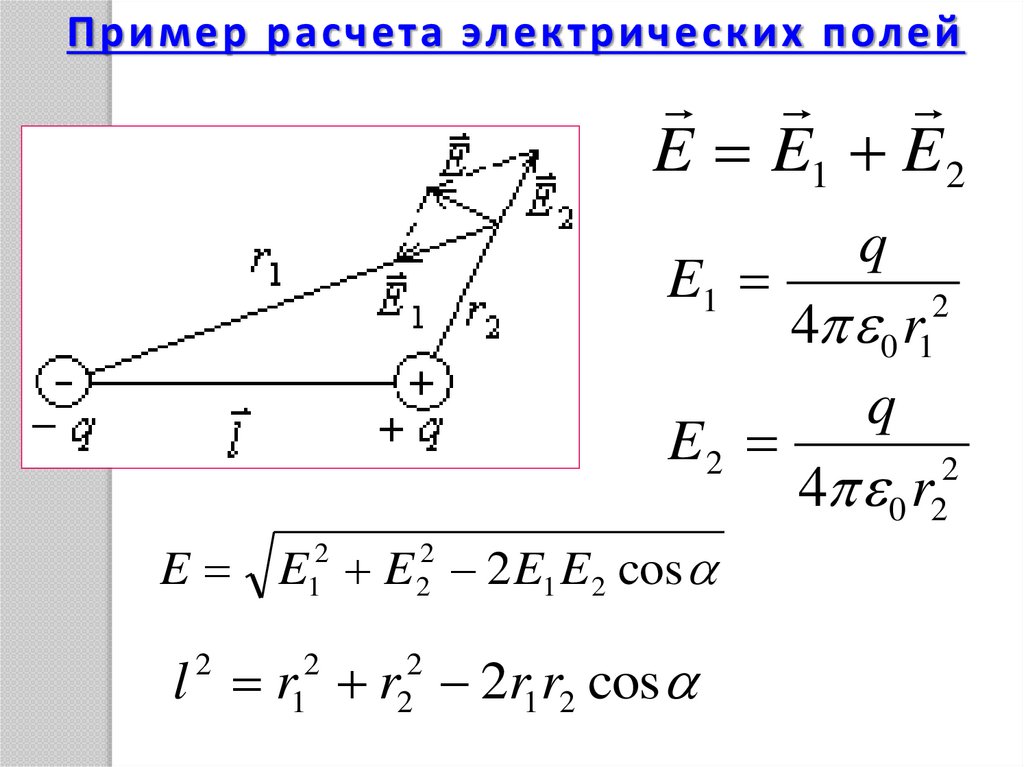
Пример расчета электрических полейE E1 E 2
E1
q
4 r
q
E2
2
4 0 r2
E E E 2 E1 E 2 cos
2
1
2
2
l r r 2r1r2 cos
2
2
1
2
2
2
0 1
33.
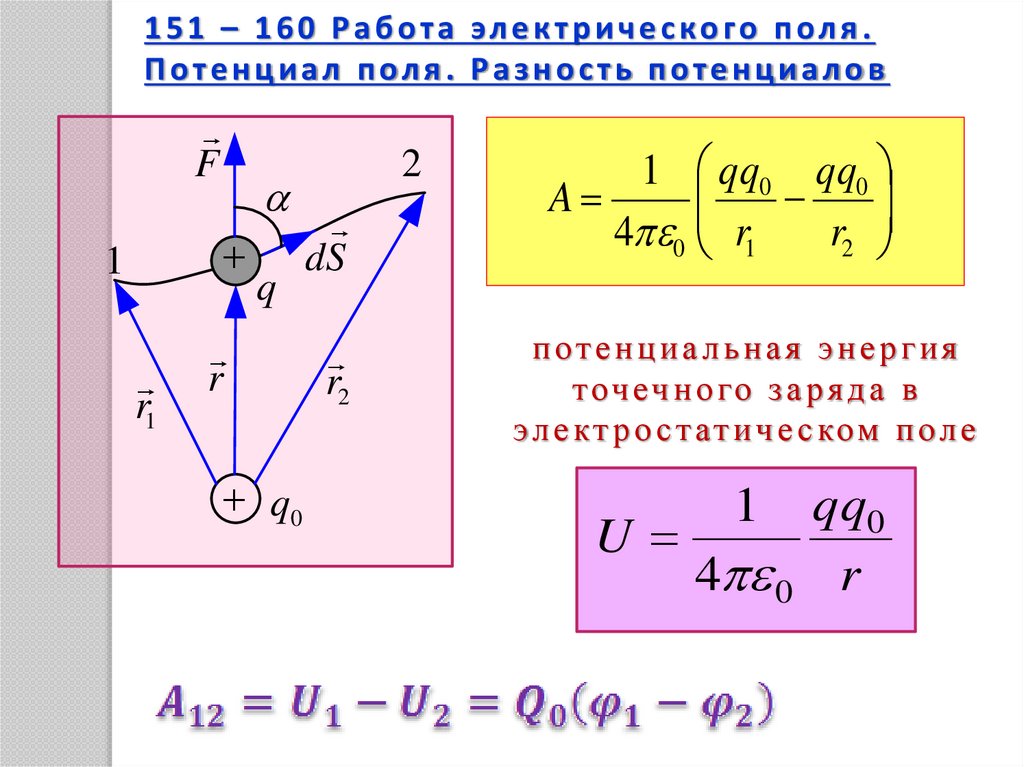
151 – 160 Работа электрического поля.Потенциал поля. Разность потенциалов
F
1
r1
q
r
q0
2
dS
r2
1 q q0 q q0
A
4 0 r1
r2
потенциальная энергия
т оч еч н о го з а р я д а в
э л е к т р о с т ат и ч е с ко м п о л е
q q0
U
4 0 r
1
34.
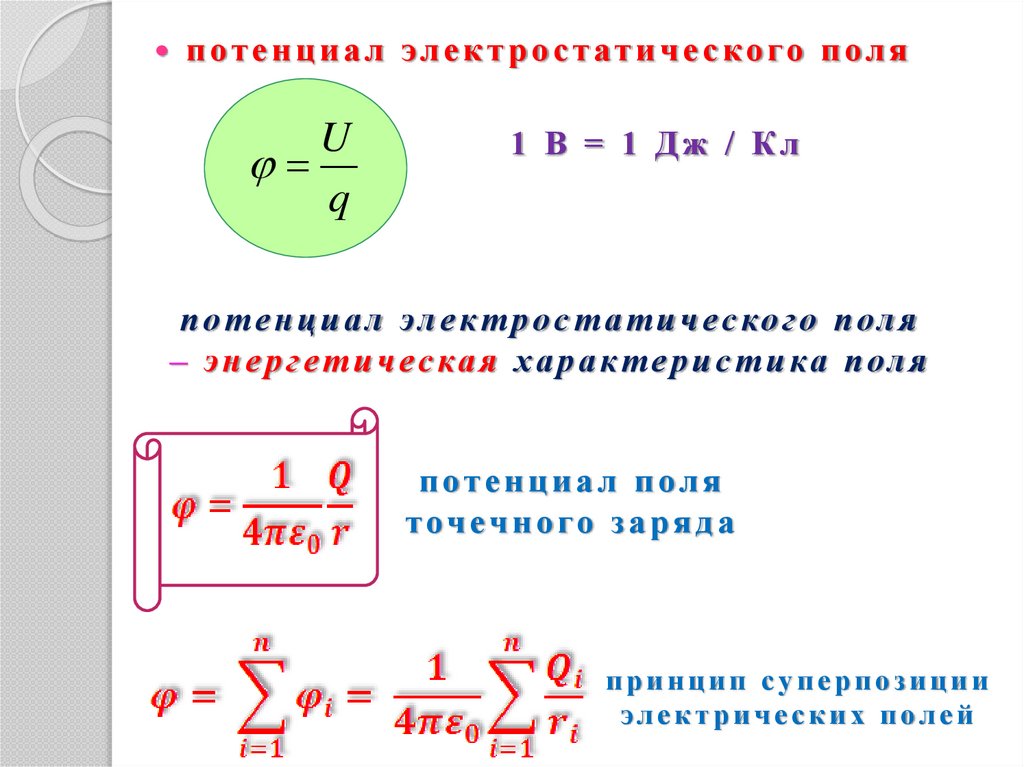
п о т е н ц и а л э л е к т р о с т ат и ч е с к о го п о л яU
q
1 В = 1 Дж / Кл
п о т е н ц и а л эл е к т р о с т а т и ч е с ко г о п ол я
– э н е р г е т и ч е с ка я х а р а к т е р и с т и ка п ол я
потенциал поля
т оч еч н о го з а р я д а
принцип суперпозиции
электрических полей
35.
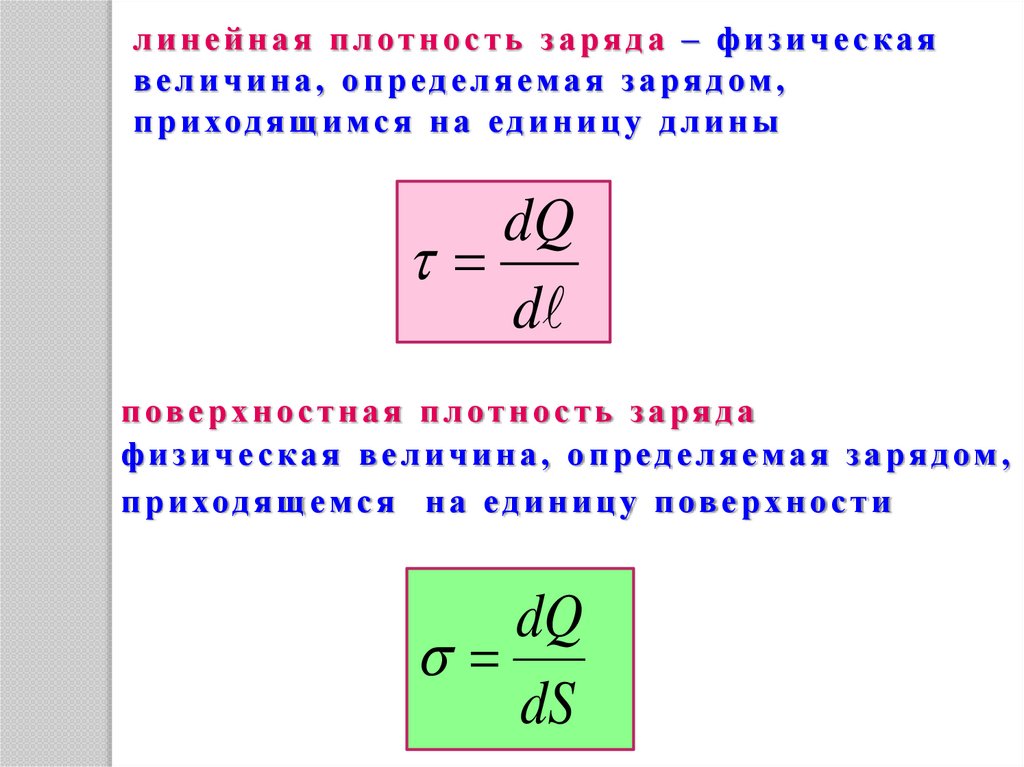
линейная плотность заряда – физическаявеличина, определяемая зарядом,
п р и ход я щ и м с я н а е д и н и ц у д л и н ы
dQ
d
п ов е р х н о с т н а я п л о т н о с т ь з а р я д а
физическая величина, определяемая зарядом,
п р и ход я щ е м с я н а е д и н и ц у п ов е р х н о с т и
dQ
dS
36.
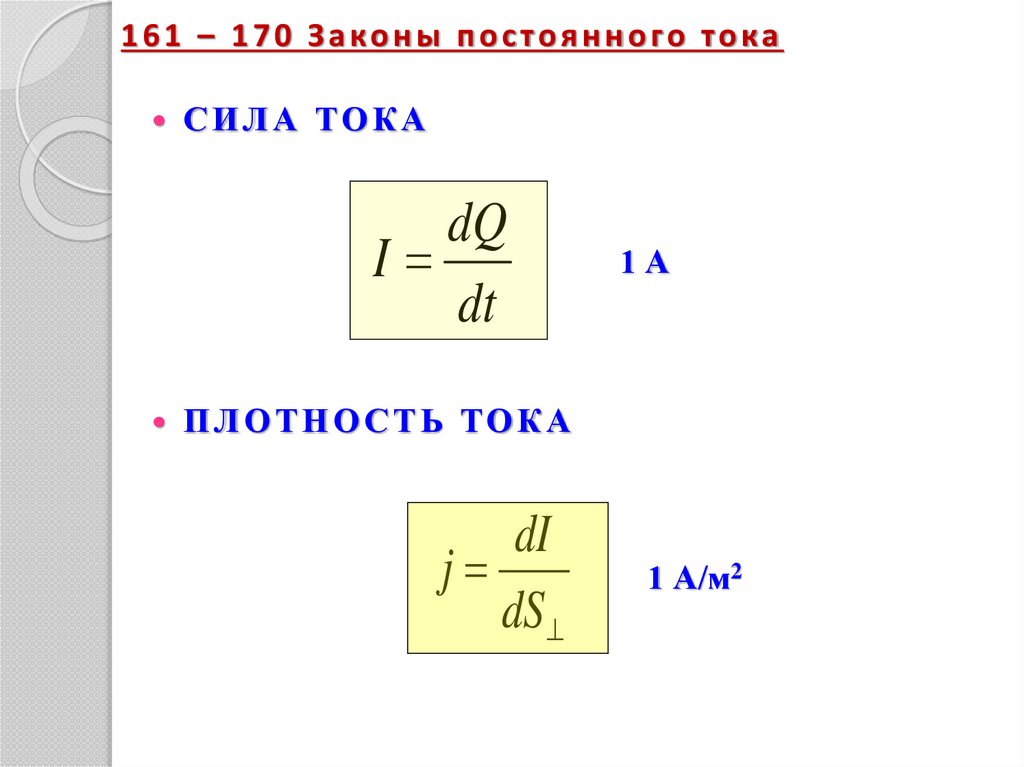
161 – 170 Законы постоянного токаСИЛА ТОКА
dQ
I
dt
1А
ПЛОТНОСТЬ ТОКА
dI
j
dS
1 А/м2
37.
н а п р я ж е н и е н а у ч а с т ке э л е к т р и ч е с к о йц е п и ( п а д е н и е н а п р я ж е н и я н а у ч а с т ке
цепи)
U12 1 2 12
з а к о н О м а д л я од н о р од н о го у ч а с т к а ц е п и
U
I
R
закон Ома в дифференциальной форме
j E
38.
З А КО Н О М А Д Л Я З А М К Н У ТО Й Ц Е П ИI
R
S
R r
сопротивление
ц и л и н д р и ч е с ко го
п р о в од н и ка
[R] = 1 Ом; [ρ] = 1 Ом · м
39.
РА Б О ТА Т О К Аd A = U I dt
М О Щ Н О С Т Ь , РАЗ В И ВА Е М А Я Т О КО М
Н А У Ч АС Т К Е Ц Е П И
P = U I = (φ1 – φ2) I + ε12I
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО
ВНЕШНЕЙ ЦЕПИ
P = U I = I2R = U2/R
40.
КО Э Ф Ф И Ц И Е Н Т П ОЛ Е З Н О ГО Д Е Й С Т В И Я ( К П Д )И С Т ОЧ Н И К А Т О К А – О Т Н О Ш Е Н И Е П ОЛ Е З Н О Й
РА Б О Т Ы К З АТ РАЧ Е Н Н О Й РА Б О Т Е
η = АПОЛ / АЗАТР
η = UВН / ε
η = RВН /(RВН + r)
41.
1 7 1 - 1 8 0 З а к о н Д ж о ул я - Л е н ц аЗ а ко н Д жоул я – Ле н ц а
dQ = I U dt = I2R dt = (U2/R)dt
З а ко н Д жоул я – Ле н ц а в
д и ф ф е р е н ц и а л ь н о й ф о рм е
w = j E = γ E2
W – УД Е Л Ь Н А Я Т Е П Л О ВА Я М О Щ Н О С Т Ь
ТОКА
КО Л И Ч Е С Т ВО Т Е П Л О Т Ы , В Ы Д Е Л Я Ю Щ Е Е С Я З А
ЕДИНИЦУ ВРЕМЕНИ В ЕДИНИЦЕ ОБЪЕМА
П Р О ВО Д Н И К А







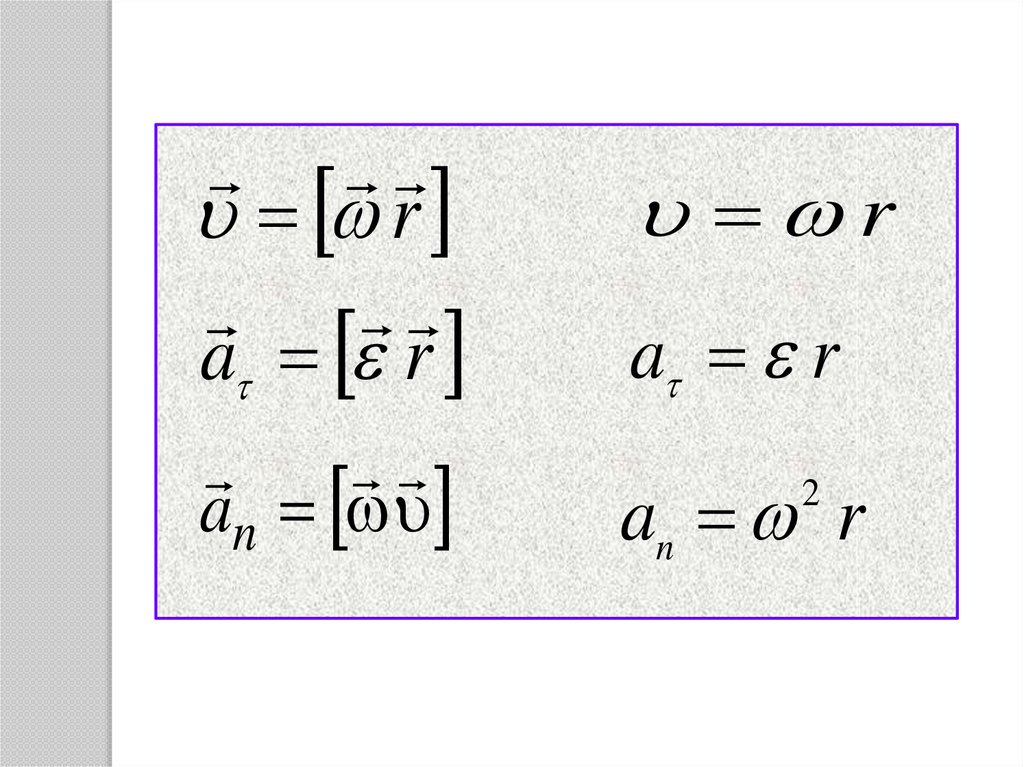





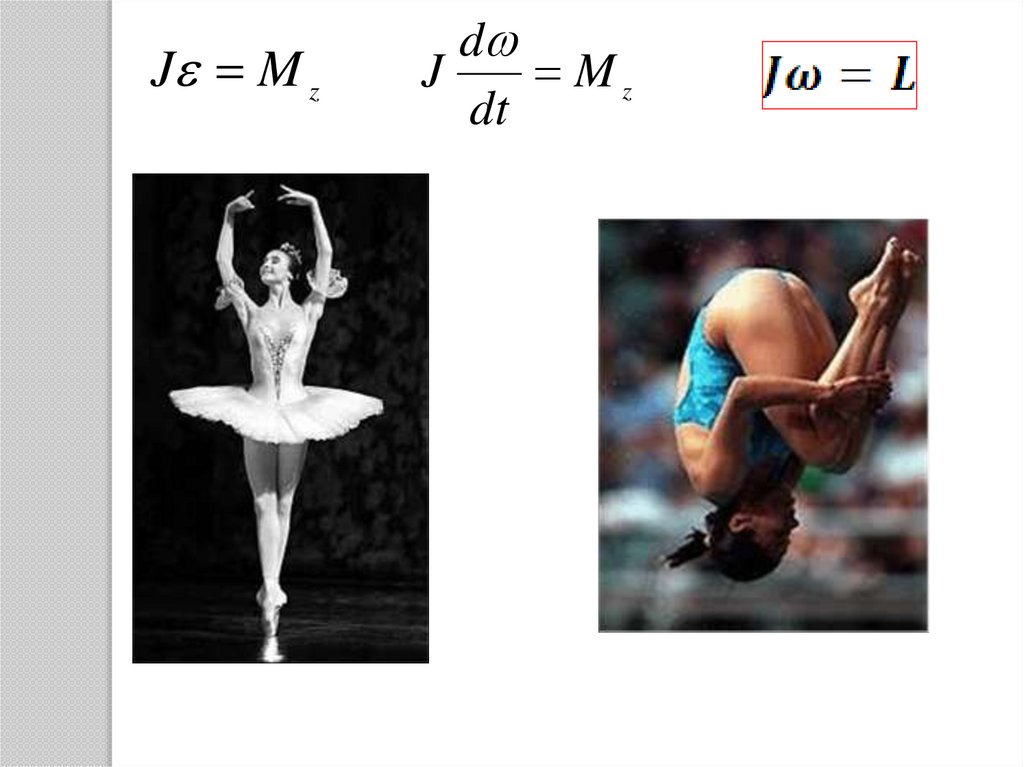








 physics
physics








