Метод гармонической линеаризации. Метод статистической линеаризации. Лекция 12

1.

РАДИОАВТОМАТИКА
Лекция 12
МЕТОД ГАРМОНИЧЕСКОЙ
ЛИНЕАРИЗАЦИИ
МЕТОД СТАТИСТИЧЕСКОЙ
ЛИНЕАРИЗАЦИИ

2. МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

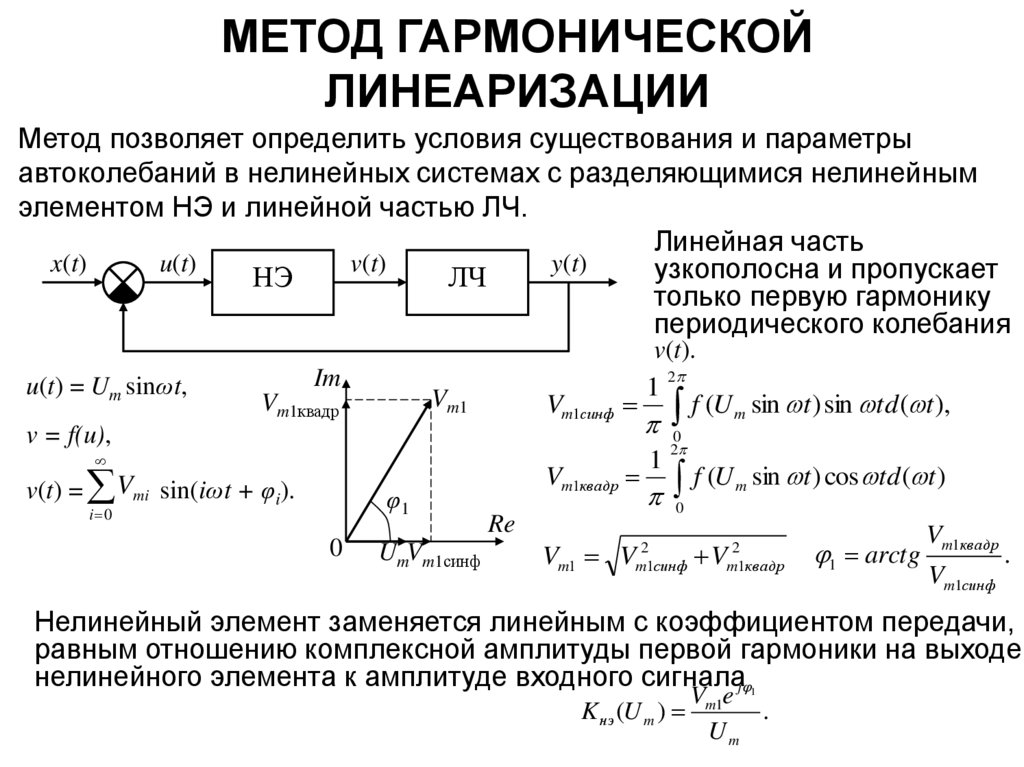
Метод позволяет определить условия существования и параметры
автоколебаний в нелинейных системах с разделяющимися нелинейным
элементом НЭ и линейной частью ЛЧ.
Линейная часть
x(t)
u(t)
v(t)
y(t)
узкополосна и пропускает
НЭ
ЛЧ
только первую гармонику
периодического колебания
u(t) = Um sinωt,
Im
v(t).
2
1
Vm1синф f (U m sin t ) sin td ( t ),
Vm1
Vm1квадр
v = f(u),
v(t) = Vmi sin(iωt + φi).
φ1
i 0
0
UmVm1синф
Vm1квадр
Re
Vm1 V
1
0
2
f (U
m
sin t ) cos td ( t )
0
2
m1синф
V
2
m1квадр
1 arctg
Vm1квадр
Vm1синф
.
Нелинейный элемент заменяется линейным с коэффициентом передачи,
равным отношению комплексной амплитуды первой гармоники на выходе
нелинейного элемента к амплитуде входного сигналаj
Vm1e 1
K нэ (U m )
.
Um

3.

Математическая модель линеаризованной системы
Согласно критерию
0
Um
Найквиста линейная система
Kнэ(Um)
Kлч(p)
будет находиться на грани
устойчивости, если
Kнэ(Um)Kнч(jω) = -1.
Пример: релейная система
АПЧ. f0 Релейный uрчд
ФНЧ
Интегратор
ЧД
ПГ
Δf = Δfmsinωt
Uрчд=f(Δfmsinωt)
uрчд
Um
ωt
Δf= f0– fпг 0 φн
0 Δfн
Δfm
φн
Δf
1
U m1синф
ωt
2
0
π
φн = arcsin(Δfн/ Δfm)
2π
2
4
f ( f m sin t ) sin td ( t ) U m sin d
н
4U m
4U
f
4U
( cos ) н 2 m cos(arcsin ( н )) m
f m
Um1квадр= 0
fпг
f н
1
f m
2

4.

K нэ ( f m )
U m1синф
f m
2
f
4U m
4U m
1 н
1 2 . Здес f н .
f m
f н
f m
f m
ь
f ( ) 1 2
0,4
0,2
0,2
0,4
0,6
0,8
1,0 α
Математическая модель линеаризованной релейной системы АПЧГ.
0
Δfm
Kнэ(Δfm)
KуптKпг
p(1+pTфнч)(1+pTпг)
Условие возникновения
автоколебаний:
Kнэ(Δfm) KуптKпг
= –1
jω(1+jωTфнч)(1+jωTпг)
Kнэ(Δfm) KуптKпг = jω3TфнчTпг + ω2(Tфнч + Tпг) – jω
Равенство мнимых частей:
0 = ω3TфнчTпг – ω;
ω1= 0, ω2 =
1
TфнчTпг
.

5.

Равенство вещественных частей:
4U m K упт K пг
f н
1
2
Kнэ(Δfm)KуптKпг = ω2(Tфнч + Tпг),
Tфнч Tпг
TфнчTпг
1
2
,
1 2
0,2
0,4
0,6
0,8
4U m K упт K пг TфнчTпг
C.
C1
C2
При С > 0,5 устанавливается режим
работы без автоколебаний.
0,2
α2
Tфнч Tпг
При С = С1 решения уравнения не
существует и автоколебания в системе
невозможны.
0,4
α1
f н
1,0 α
При С = С2 существует два решения
уравнения: α1 и α2. Одно из них (α1)
соответствует устойчивому режиму
работы, другое (α2) – неустойчивому.
Амплитуда автоколебаний определится из выражения α = α1: Δfm= Δfн/ α1.

6. МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

v = f(u)
x(t)
u(t)
НЭ
K(p)
v(t)
ЛЧ
y(t)
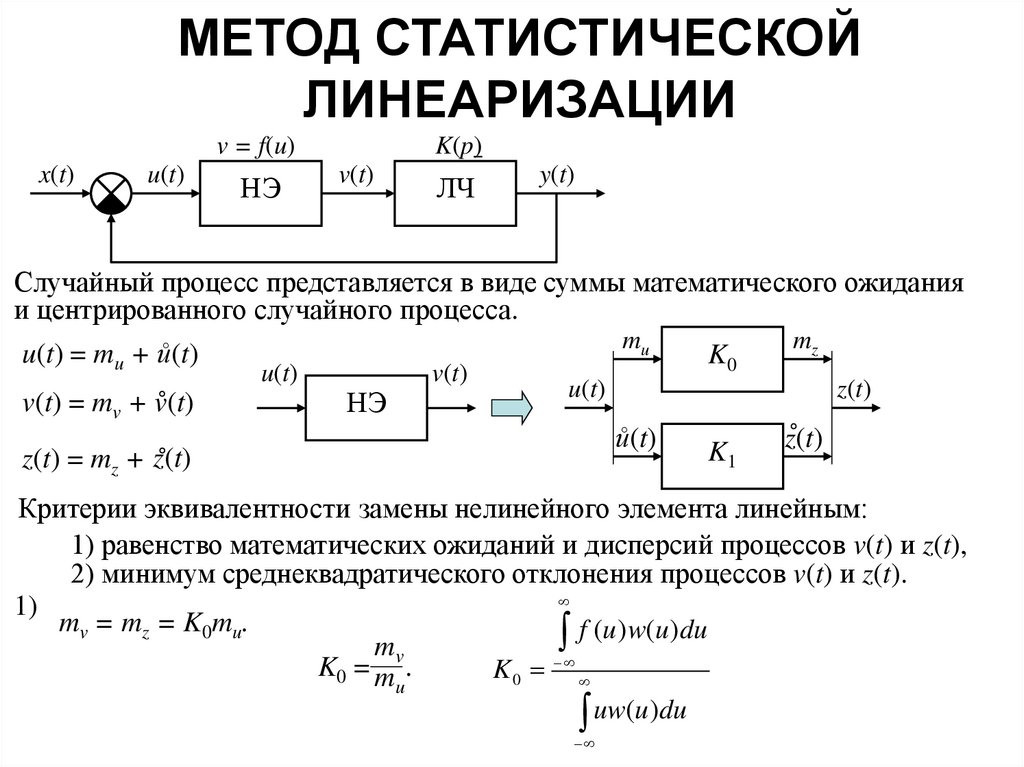
Случайный процесс представляется в виде суммы математического ожидания
и центрированного случайного процесса.
u(t) = mu + ů(t)
v(t) = mv + v(t)
mu
u(t)
v(t)
НЭ
K0
mz
u(t)
z(t)
ů(t)
z(t) = mz + z(t)
K1
z(t)
Критерии эквивалентности замены нелинейного элемента линейным:
1) равенство математических ожиданий и дисперсий процессов v(t) и z(t),
2) минимум среднеквадратического отклонения процессов v(t) и z(t).
1)
mv = mz = K0mu.
f (u)w(u)du
mv
K0 = m .
K0
u
uw(u)du

7.

v2 z2 K12 u2
2
f
(
u
)
m
w(u )du
v
v2
K1
u2
2)
.
2
u
m
w(u )du
u
v(t ) z (t ) 2 σ2 = min
2 = (mv + v(t) – K0mu – K1ů(t))2 =
(mv2 + v2(t) + K02mu2 + K12ů2(t) + 2mvv(t) – 2mvK0mu – 2mvK1ů(t) – 2v(t)K0mu –
– 2v(t)K1ů(t) + 2K0muK1ů(t) = mv2 + σv2 + K02mu2 + K12 σu2 – 2K0mvmu – 2K1v(t)ů(t)
Минимум
σ2
по K0:
Минимум σ2 по K1:
d 2
0.
dK 0
2K0mu2 – 2mvmu = 0
d 2
0. 2K1 σu2 – 2v(t)ů(t) = 0.
dK1
K0
K1
f (u) m u m w(u)du
v
K1
u
2
(
u
m
)
w(u )du
u
.
mv
.
mu
K vu (0)
u2

8.

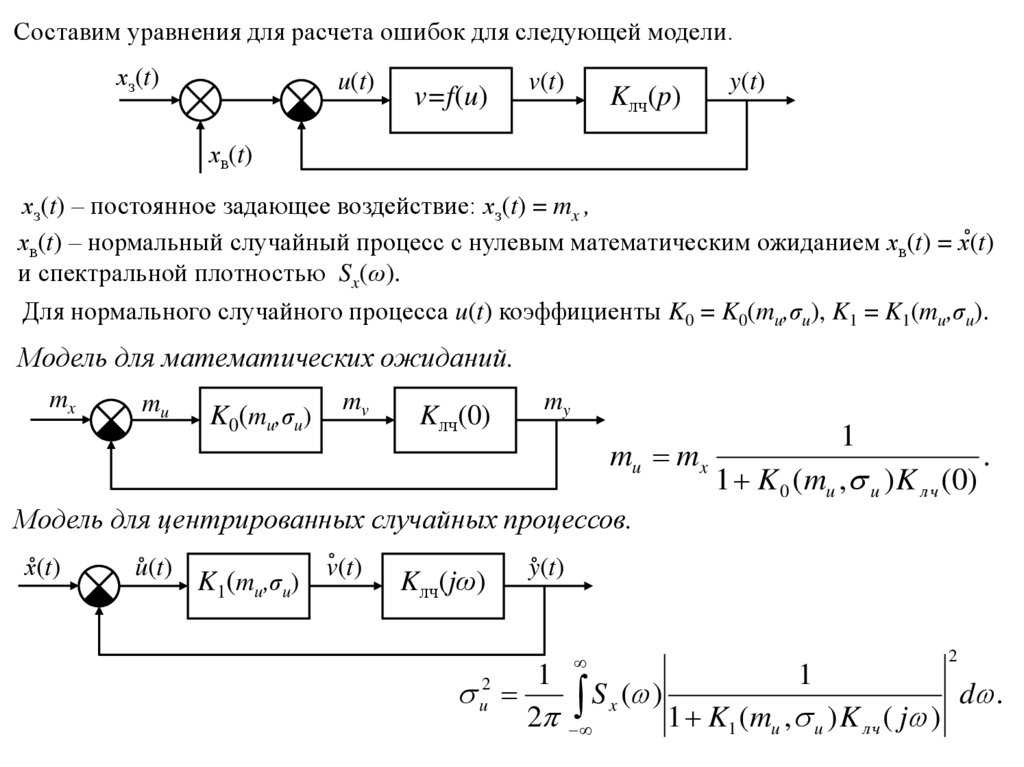
Составим уравнения для расчета ошибок для следующей модели.
хз(t)
u(t)
v=f(u)
v(t)
Kлч(p)
y(t)
хв(t)
хз(t) – постоянное задающее воздействие: хз(t) = mx ,
хв(t) – нормальный случайный процесс с нулевым математическим ожиданием хв(t) = х(t)
и спектральной плотностью Sx(ω).
Для нормального случайного процесса u(t) коэффициенты K0 = K0(mu,σu), K1 = K1(mu,σu).
Модель для математических ожиданий.
mx
mu
K0(mu,σu)
mv
Kлч(0)
my
mu mx
1
.
1 K 0 (mu , u ) K лч (0)
Модель для центрированных случайных процессов.
х(t)
u(t)
K1(mu,σu)
v(t)
Kлч(jω)
u2
y(t)
1
2
S x ( )
1
1 K1 (mu , u ) K лч ( j )
2
d .