Similar presentations:
Лекція 3. Розтяг та стиск прямого бруса
1.
Лекція 3І. РОЗТЯГ ТА СТИСК ПРЯМОГО БРУСА
1.Внутрішні зусилля: поздовжні сили.
2.Нормальні напруження.
3.Поздовжні та поперечні деформації.
ІІ. МЕХАНІЧНІ ХАРАКТЕРИСТИКИ МАТЕРІАЛІВ.
Центральний розтяг (стиск). У багатьох елементах конструкцій виникають тільки
поздовжні зусилля, що викликають у них деформації розтягу або стиску (стійки, елементи
ферм, тяги, троси і т.п.). Таким чином, розтяг (стиск) стержнів виникає при дії на них
сил, прикладених по поздовжній осі цих стержнів.
F1
a
F2
b
z
c
Прийняті гіпотези при розгляді деформацій розтягу (стиску).
Принцип Сен-Венана - Якщо сукупність деяких сил, прикладених до невеликої частини
поверхні тіла, замінити статично еквівалентною системою інших сил, то така заміна не
викличе суттєвих змін в умовах навантаження частин тіла, досить віддалених від місць
прикладання вихідної системи сил. Як показує досвід, за межами цієї області деформації
практично постійні і поперечні перерізи переміщуються паралельно своїм початковим
положенням. На підставі цього вводиться гіпотеза плоских перерізів (Я. Бернуллі):
поперечні перерізи стержня, плоскі і перпендикулярні до осі стержня до деформації,
залишаються плоскими і перпендикулярними після деформації.
2.
ВНУТРІШНІ ЗУСИЛЛЯПід
дією зовнішніх
сил
на об'єкт
відбувається
зміна відстаней
між частинками
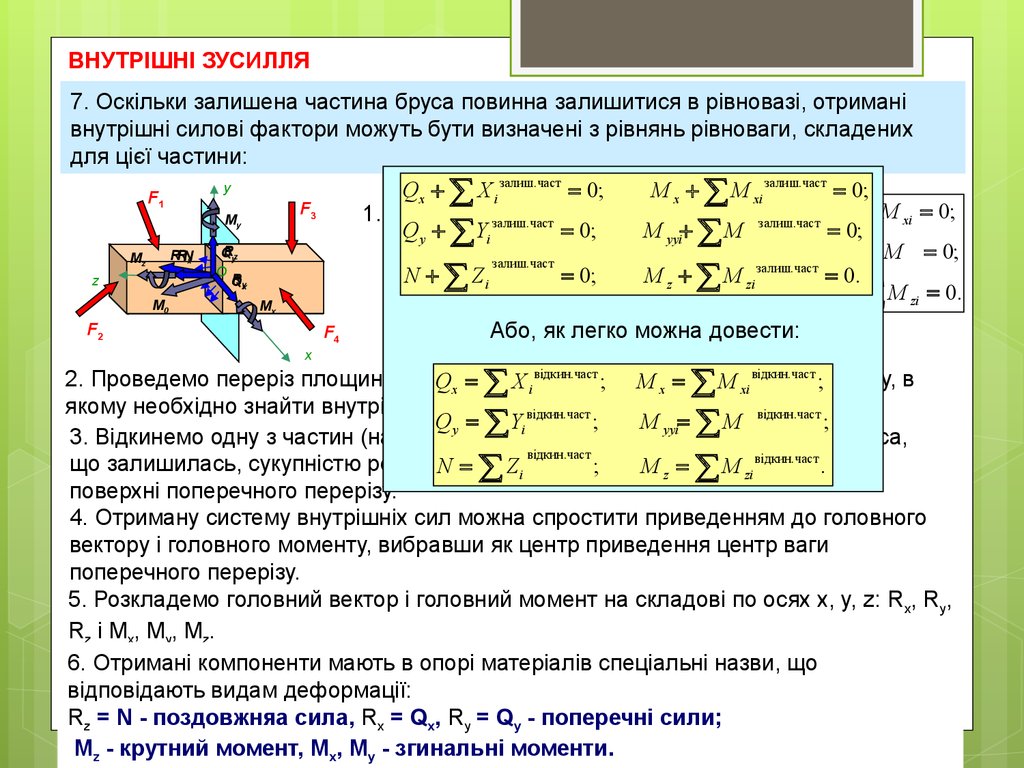
7. Оскільки
залишена
частина
бруса
повинна залишитися
в рівновазі,
отримані
(атомами)
розглянутого
тіла
і
сил
взаємодії
між
ними.
В
результаті
виникають
так
внутрішні силові фактори можуть бути визначені з рівнянь рівноваги, складених
звані
внутрішні
для цієї
частини:сили, які можна визначити методом перерізів :
y
F1
F3
My
RRNx
Mz
z
M0
Ryz
Q
O
Ryx
Q
Mx
F2
F4
x
Qx + å X i залиш.част = 0;
M x + å M xi залиш.част = 0;
1. Нехай брус
під дією сил F1,
å X i = 0; å M xi = 0;
Qy + å Yi залиш.част = 0;
M yуi+ å M залиш.част = 0;
F2, ... Перебуває в рівновазі.
å Yзалиш.част
å M = 0;
iуi= 0;
залиш.част
N+å
Zi
= 0;
M z + å M zi
= 0.
Для
даного
об'єкту
Z
=
0;
å i
å M zi = 0.
задовольняються рівняння
рівноваги:
Або, як легко можна довести:
відкин.част
2. Проведемо переріз площиною, що
з поперечним
перерізом
Qx співпадає
= å X i відкин.част
; Mx = åM
; брусу, в
xi
якому необхідно знайти внутрішні сили.
Qy = å Yi відкин.част ;
M yуi= å M відкин.част ;
3. Відкинемо одну з частин (наприклад, ліву) і замінимо її дію на частину бруса,
відкин.част
що залишилась, сукупністю реактивних
чином
N = åсил,
Z i розподілених
;
M z =деяким
. по
å M zi відкин.част
поверхні поперечного перерізу.
4. Отриману систему внутрішніх сил можна спростити приведенням до головного
вектору і головного моменту, вибравши як центр приведення центр ваги
поперечного перерізу.
5. Розкладемо головний вектор і головний момент на складові по осях x, y, z: Rx, Ry,
Rz і Mx, My, Mz.
6. Отримані компоненти мають в опорі матеріалів спеціальні назви, що
відповідають видам деформації:
Rz = N - поздовжняа сила, Rx = Qx, Ry = Qy - поперечні сили;
Mz - крутний момент, Mx, My - згинальні моменти.
3.
1. Внутрішні зусилля при розтязі-стиску - при розтязі-стиску в поперечному перерізістержня виникає лише один силовий фактор - поздовжня сила N.
Відповідно до методу перерізів величина і напрям поздовжньої сили можуть бути
знайдені з рівняння рівноваги проекції на вісь, що збігається з віссю стержня,
складеного для залишеної частини:
N + å Zi
залиш.частини
=0
Þ
N = å Zi
залиш.частини
Поздовжня сила вважається позитивною, якщо вона викликає розтяг, тобто
спрямована від перерізу:
F
z
Поздовжня сила вважається негативною, якщо вона викликає стиск, тобто
направлена до перерізу.
F
z
4.
Нехай стержень завантажений поздовжніми зосередженими силами F1, F2:F2=100кН
F1=250кН
RD
III
II
I
z
1. Знайдемо опорну реакцію:
II
D
C
B I
A
Z = 0; - F2 + F1 + RD = 0;
III
=150кН
a=2м
b=3м
c=1м
å
z3
z2
NI-I
NII-II
NIII-III
F1
F2
F2
z1
RD = F2 - FкН
1 = 100 - 250 = -150
2. Визначимо значення
поздовжньої сили:
ДІЛЯНКА АВ
перерріз І-І: 0 ≤ z1 ≤ 1м
N І -І = 0
ДІЛЯНКА ВС
перерріз ІІ-ІІ:
1м ≤ z2 ≤ 4м
N ІІ - ІІ = - FкН
2 = -100
ДІЛЯНКА СD
перерріз IІІ-IІІ:
4м ≤ z3 ≤ 6м
N ІІІ - ІІІ = - F2 + F1 =
= -100 + 250 = 150кН
Будуємо епюру N:
Поздовжня сила в перерізі дорівнює алгебраїчній
сумі проекцій на вісь бруса сил, взятих по одну сторону від перерізу:
N = å Fziправ =å Fziлiв .
.
5.
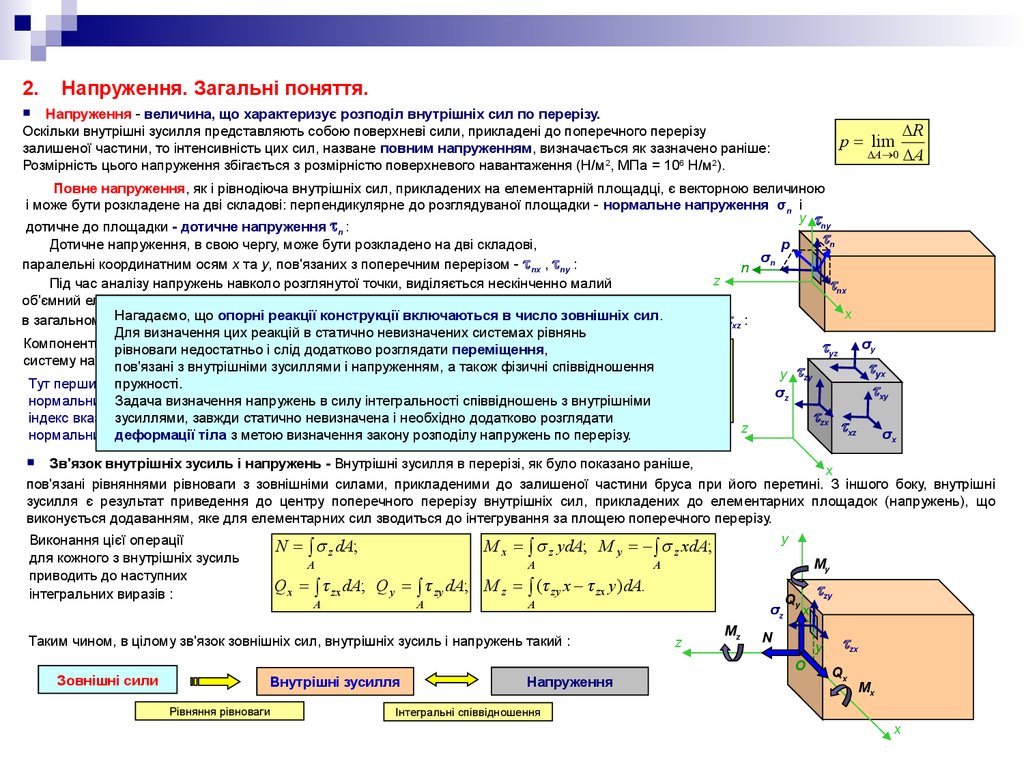
2.Напруження. Загальні поняття.
Напруження - величина, що характеризує розподіл внутрішніх сил по перерізу.
Оскільки внутрішні зусилля представляють собою поверхневі сили, прикладені до поперечного перерізу
залишеної частини, то інтенсивність цих сил, назване повним напруженням, визначається як зазначено раніше:
Розмірність цього напруження збігається з розмірністю поверхневого навантаження (Н/м2, МПа = 106 Н/м2).
R
A 0 A
p = lim
Повне напруження, як і рівнодіюча внутрішніх сил, прикладених на елементарній площадці, є векторною величиною
і може бути розкладене на дві складові: перпендикулярне до розглядуваної площадки - нормальне напруження σn і
y ny
дотичне до площадки - дотичне напруження n :
n
Дотичне напруження, в свою чергу, може бути розкладено на дві складові,
p
σ
паралельні координатним осям x та y, пов'язаних з поперечним перерізом - nx , ny :
n n
z
Під час аналізу напружень навколо розглянутої точки, виділяється нескінченно малий
nx
об'ємний елемент (паралелепіпед зі сторонами dx, dy, dz), по кожній грані якого діють,
x
Нагадаємо,
опорні реакції
конструкції
включаються
в число
сил.x) -σ , , :
в загальному випадку,
три що
напруження,
наприклад,
для грані,
перпендикулярній
осізовнішніх
x (площадка
x
xy
xz
Для визначення цих реакцій в статично невизначених системах рівнянь
Компоненти напружень
трьом перпендикулярним
елемента
утворюють
yz σy
рівноваги по
недостатньо
і слід додатковограням
розглядати
переміщення,
x yx zx
систему напружень,
описувану
так
званим
тензором
напружень:
пов'язані з внутрішніми зусиллями і напруженням, а також фізичні співвідношення
yx
y zy
T = xy y zy
пружності.
Тут перший стовпець
представляє компоненти напружень на площадках,
xy
σz
Задача
напружень
силу
інтегральності
співвідношень з внутрішніми
нормальних до
осі x, визначення
другий і третій
- до осі yв та
z відповідно.
перший
xz
yz
z
zx
завжди статично
і необхідно додатково розглядати
індекс вказує зусиллями,
площадку ("місце")
дії, другийневизначена
- напрям. Для
xz σ
z
деформації
тіла з збігаються
метою визначення
закону
розподілу напружень по перерізу.
нормальних напружень
індекси
і один індекс
опускається.
x
Зв'язок внутрішніх зусиль і напружень - Внутрішні зусилля в перерізі, як було показано раніше,
x
пов'язані рівняннями рівноваги з зовнішніми силами, прикладеними до залишеної частини бруса при його перетині. З іншого боку, внутрішні
зусилля є результат приведення до центру поперечного перерізу внутрішніх сил, прикладених до елементарних площадок (напружень), що
виконується додаванням, яке для елементарних сил зводиться до інтегрування за площею поперечного перерізу.
y
Виконання цієї операції
M x = z ydA; M y = - z xdA;
N = z dA;
для кожного з внутрішніх зусиль
A
A
A
My
приводить до наступних
Q x = zx dA; Q y = zy dA; M z = ( zy x - zx y )dA.
zy
інтегральних виразів :
Qy
A
A
A
σz x
Mz
N
Таким чином, в цілому зв'язок зовнішніх сил, внутрішніх зусиль і напружень такий :
z
y zx
O
Qx
Зовнішні сили
Напруження
Внутрішні зусилля
M
x
Рівняння рівноваги
Інтегральні співвідношення
x
6.
Напруження при розтязі (стиску) - Як було раніше сказано, задача визначення напруженьзавжди є статично невизначеною. Такі задачі вирішуються послідовним розглядом статичної,
геометричної і фізичної сторін. В даному випадку маємо статичне рівняння, що зв'язує внутрішнє
зусилля - поздовжню силу - з напруженням:
N = dA.
z
A
Для обчислення інтеграла необхідно знати закон зміни напружень по перерізу. Цей закон можна
встановити вивченням безпосередньо досліджуваних переміщень (деформацій). Оскільки приймається
гіпотеза плоских перерізів, то при відсутності зовнішнього розподіленого поздовжнього навантаження,
деформації постійні по перерізу і по довжині стержня (геометрія).
Деформації у точці:
dz
l
ez =
= const.
e позд = e z = ,
dz
l
де l – абсолютна поздовжня деформація (видовження), l - довжина (базова довжина) стержня.
Дослідним шляхом встановлений фундаментальний (фізичний) зв'язок зусиль і видовжень (Р. Гук) в
наступному вигляді: = Ee ,
де Е – модуль пружності (фізична постійна матеріалу, що визначається експериментально).
Підстановка останнього співвідношення - закону Гука - в інтегральний вираз із урахуванням
постійного значення деформацій та напружень дає :
N = z dA = z A;
A
z =
N
.
A
Нормальні напруження при розтязі (стиску) в поперечному перерізі прямо пропорційно
величині поздовжнього зусилля і обернено пропорційно площі перерізу.
7.
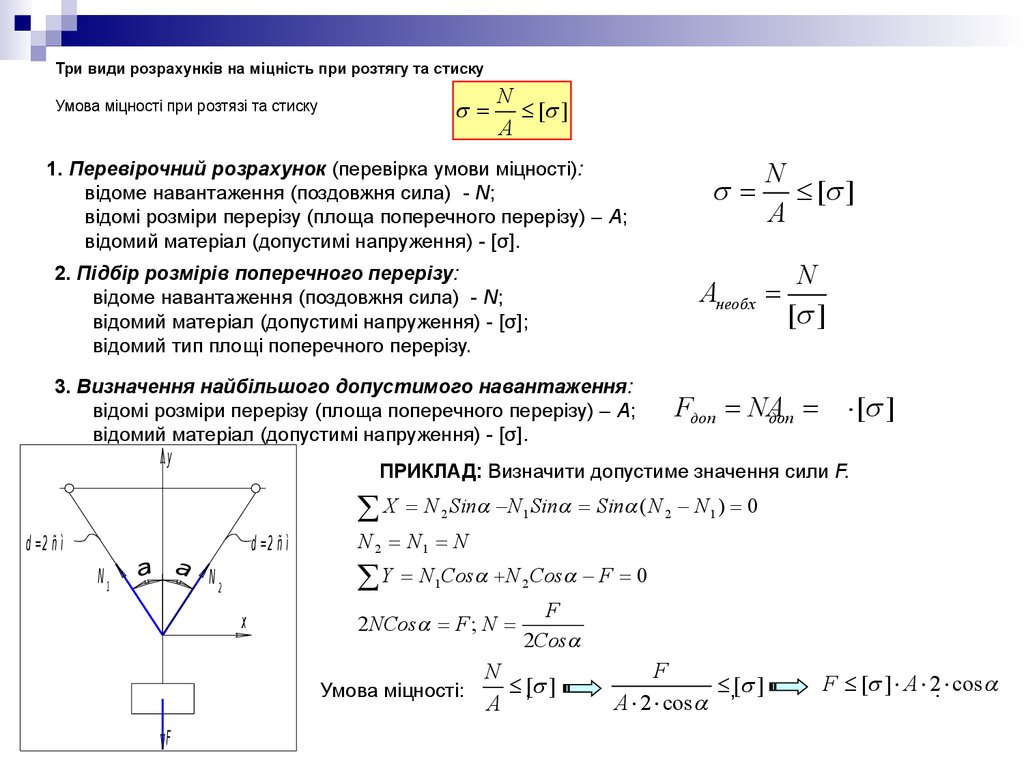
Три види розрахунків на міцність при розтягу та стиску=
Умова міцності при розтязі та стиску
N
£ [ ]
A
1. Перевірочний розрахунок (перевірка умови міцності):
відоме навантаження (поздовжня сила) - N;
відомі розміри перерізу (площа поперечного перерізу) – А;
відомий матеріал (допустимі напруження) - [σ].
2. Підбір розмірів поперечного перерізу:
відоме навантаження (поздовжня сила) - N;
відомий матеріал (допустимі напруження) - [σ];
відомий тип площі поперечного перерізу.
=
Aнеобх
N
£ [ ]
A
N
=
[ ]
3. Визначення найбільшого допустимого навантаження:
Fдоп = NА
× [ ]
відомі розміри перерізу (площа поперечного перерізу) – А;
доп =
відомий матеріал (допустимі напруження) - [σ].
y
ПРИКЛАД: Визначити допустиме значення сили F.
åХ = N
d =2 ñ ì
d =2 ñ ì
N1
2
Sin -N 1 Sin = Sin ( N 2 - N 1 ) = 0
N 2 = N1 = N
å Y = N Cos +N Cos - F = 0
N2
1
x
2 NCos = F ; N =
Умова міцності:
F
2
F
2Cos
N
£ ,[ ]
A
F
£,[ ]
A × 2 × cos
F £ [ ] × A × 2. × cos
8.
3.Деформації. Загальні поняття.
Переміщення – перехід точок тіла в нове положення внаслідок зміни форми і розмірів тіла під дією навантаження.
Повне переміщення точки в просторі розкладається на компоненти u, v і w, паралельні осям x, y і z, відповідно.
Переміщення розглядуваної точки залежить від деформації всіх навантажених областей тіла і включає в себе переміщення як жорсткого
цілого ненавантажених областей. Таким чином, переміщення не може характеризувати ступінь деформування навколо
розглядуваної точки.
■
Деформація в точці - міра деформування матеріалу навколо точки. Виділимо в даній точці тіла елементарний
об’єм (паралелепіпед зі сторонами dx, dy, dz) і розглянемо його можливі зміни розмірів і форми.
Нехай за рахунок деформації довжини його ребер отримають абсолютні видовження dx, dy та dz:
Відносні лінійні деформації в точці :
ex =
dx
dy
dz
; ey =
; ez =
.
dx
dy
dz
Крім лінійних деформацій, пов'язаних зі зміною розмірів лінійних
елементів, виникають кутові деформації або
кути зсуву, пов'язані зі зміною форми.
x
Наприклад, у площині xy можуть виникати малі
dy
зміни прямих кутів паралелепіпеда :
z
dy
dy
x
y
= tg xy xy .
y
dy
xy
x
dx
dx
dz
dx
Такі кутові деформації в загальному випадку можуть мати місце у всіх трьох
x
1
площинах. Всі відносні деформації досить малі і мають для реальних
ex
yx
-4
-3
матеріалів порядок ≈10 -10 .
2
Таким чином, сукупність відносних лінійних і кутових деформацій визначають деформований
1
Te = xy
ey
стан в точці і утворюють тензор деформацій, подібний тензора напружень:
2
Примітка: Половинні кути зсуву використовуються з метою отримання аналогічних формул перетворення з
1
1
тензором напружень.
yz
xz
2
2
Залежно від того, які з компонент відносних деформацій мають нульове значення
в даній області або для всього тіла, розрізняють такі прості види деформацій:
1. Лінійна деформація - εz ≠ 0, кути зсуву дорівнюють нулю, іншими лінійними відносними деформаціями нехтується
(Характеризується абсолютним і відносним подовженням).
2. Плоска деформація - εz ≠ 0, εx ≠ 0 або εy ≠ 0, інші відносні деформації дорівнюють нулю (характеризується абсолютним і
відносним звуженням площі поперечного перерізу). Ці види деформацій зазвичай реалізуються при розтязі-стиску.
3. Об'ємна деформація - εz ≠ 0, εx ≠ 0, εy ≠ 0, кути зсуву дорівнюють нулю (характеризується абсолютною і відносною зміною об’єму).
4. Чистий зсув - лінійні відносні деформації дорівнюють нулю, кути зсуву не рівні нулю (характеризується зміною форми,
зміна об’єму не відбувається). Цей вид деформації також виникає при крученні.
Відповідно до виду деформації спочатку послідовно вивчають такі найпростіші напружено-деформовані стани як
розтяг-стиск, чистий зсув і кручення, чистий згин. Далі вивчаються більш складні - поперечний згин, складний опір,
поздовжній згин.
dz
1
zx
2
1
zy
2
ez
9.
Деформації при розтязі (стиску)Абсолютна деформація:
Відносна деформація:
l = l0 - l1.
l l - l
e= = 0 1.
l0
l0
Абсолютну деформацію (видовження) стержня також можна визначити через поздовжнє
зусилля (отримана таким чином залежність називається законом Гука в розгорнутому
вигляді):
Nl
l = e z l =
E
l =
l.
EA
.
Формула для абсолютного видовження справедлива лише при постійній по довжині
стержня поздовжній силі і незмінній площі поперечного перерізу!
У разі змінної поздовжньої сили, наприклад, при врахуванні власної ваги вертикальних
стержнів, та / або змінної площі необхідно використовувати інтегральний вираз:
l
l =
0
Ndz
.
EA
10.
Коефіцієнт Пуассона - при розтягу стержня поряд з поздовжньою деформацією (видовженням), якевизначається законом Гука, виникає поперечна деформація (звуження поперечного перерізу), що
виражається в зменшенні поперечних розмірів стержня. Відносні поперечні деформації обчислюються
як
b
a де b, a - розміри поперечного перерізу.
e попер = e x = -
b
,
e попер = e y = -
a
,
Експериментально встановлено, що існує лінійний зв'язок
між поздовжньої і поперечної деформацією:
e попер = -n × e позд
Матеріал
Сталь
0,25-0,33
Мідь, бронза
0,31-0,35
Чавун
0,23-0,27
де ν – коефіцієнт пропорційності, що називається коефіцієнтом Пуассона.
Бетон
Коефіцієнт Пуассона для певного матеріалу в межах пружних деформацій
має постійне значення і знаходиться в межах від 0 до 0,5.
Деревина:
За законом Гука, який визначає зв'язок нормальних напружень
з поздовжніми деформаціями:
ez = z .
E
тоді e = e = -n × e = -n × z .
x
y
z
ν
вздовж волокон
поперек волокон
0,08-0, 18
0,5
0,02
Алюміній
0,32-0,36
Гума, каучук
0,47-0,5
E
Як згадувалося раніше, в загальному випадку навантаження, по гранях
виділеного елемента виникають нормальні і дотичні напруження. Останні,
викликаючи деформації зсуву і не впливають на лінійні деформації, оскільки
не змінюють довжин сторін елемента. Використовуючи принцип
незалежності дії сил, справедливий для ізотропного і лінійно пружного
матеріалу, можна записати узагальнений закон Гука, що враховує
одночасну дію нормальних напружень по всіх гранях елемента:
1
[ x -n × ( y + z )];
E
1
e y = [ y -n × ( z + x )];
E
1
e z = [ z -n × ( x + y )].
E
ex =
11.
МЕХАНІЧНІ ХАРАКТЕРИСТИКИ МАТЕРІАЛІВКласифікація випробувань
А. По характеру навантаження:
1. статичні;
2. динамічні.
В. По виду деформацій:
1. на розтяг (випробовують пластичні матеріали);
2. на стиск (випробовують крихкі матеріали);
3. на зсув (зріз);
4. на згин;
5. на кручення;
6. на складні види деформацій (при складному напруженому стані).
С. По технології проведення випробувань
(розміри зразків, кількість і тип вимірювальних приладів тощо).
12.
Випробування матеріалів на розтяг – стиск.При проектуванні конструкцій, машин і механізмів необхідно знати міцнісні і деформаційні властивості
матеріалів. Їх визначають експериментально на спеціальних випробувальних машинах. З усіх
властивостей (твердість, опірність ударним навантаженням, протидія високим або низьким
температурам і т.п.) основними є опір на розтягування і стиснення, що дають найбільшу і
найважливішу інформацію про механічні властивості металів.
d
Випробування на розтяг – проводять на розривних
або універсальних машинах, які мають спеціальні
захвати для передачі зусилля.
Використовуються стандартні зразки спеціальної форми
(l0 – довжина робочої частини,
l0/ a0 = 5 – короткі,
l0
a0
b0
l0/ a0 = 10 – довгі).
l0
При випробуваннях на стиск застосовуються циліндричні зразки з
відношенням висоти до діаметра h/d = 1,5 – 3. Зразки встановлюються на
опорну поверхню з використанням мастила для ослаблення впливу сил тертя.
Всі машини обладнані пристроєм для автоматичного запису в певному масштабі діаграми-графіка
залежності величини розтягуючої сили від подовження зразка. Сучасні машини комп'ютеризовані і
мають засоби управління процесом навантаження по різним заданим програмам, виведення даних
на екран і збереження їх у файлах для подальшої обробки.
13.
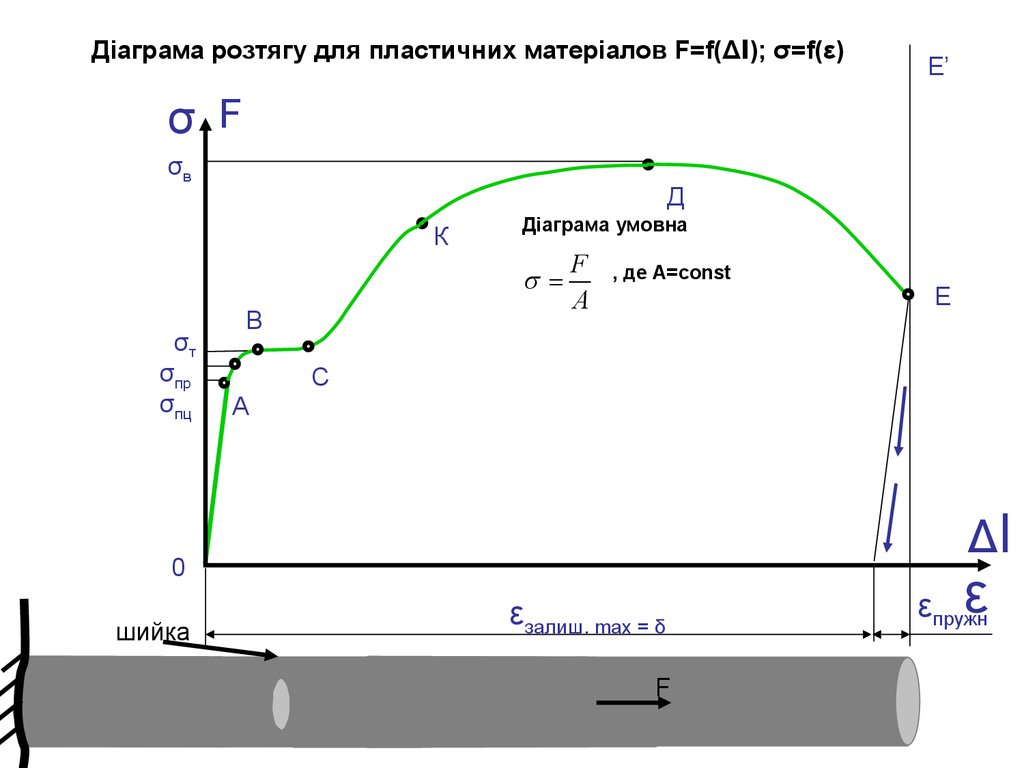
Діаграма розтягу для пластичних матеріалов F=f(Δl); σ=f(ε)Е’
σ F
σв
Д
Діаграма умовна
К
=
σт
σпр
σпц
В
F
A
, де A=const
Е
С
А
Δl
0
εзалиш. max = δ
шийка
F FF F F
F
F
ε
εпружн
14.
σпц – Межа пропорційності – найбільше напруження, до якого існує пропорційна залежність міжнавантаженням і деформацією (справжнюється закон Гука) (для Ст3 σпц =195-200 МПа).
пц =
Fпц
.
A0
σпр – Межа пружності – найбільше напруження, при якому в матеріалі не виявляється ознак
пластичної (залишкової) деформації (для Ст3 σпр =205-210 МПа).
F
пр =
пр
A0
.
σт – Межа текучості – найменше напруження, при якому зразок деформується без помітного
збільшення розтягуючого навантаження (для Ст3 σт =220-250 МПа).
F
т =
т
A0
.
σв – Межа міцності або тимчасовий опір – напруження, що відповідає найбільшому навантаженню,
Fмакс
що передбачає руйнування зразка (для Ст3 σв =370-470 МПа).
в =
A0
.
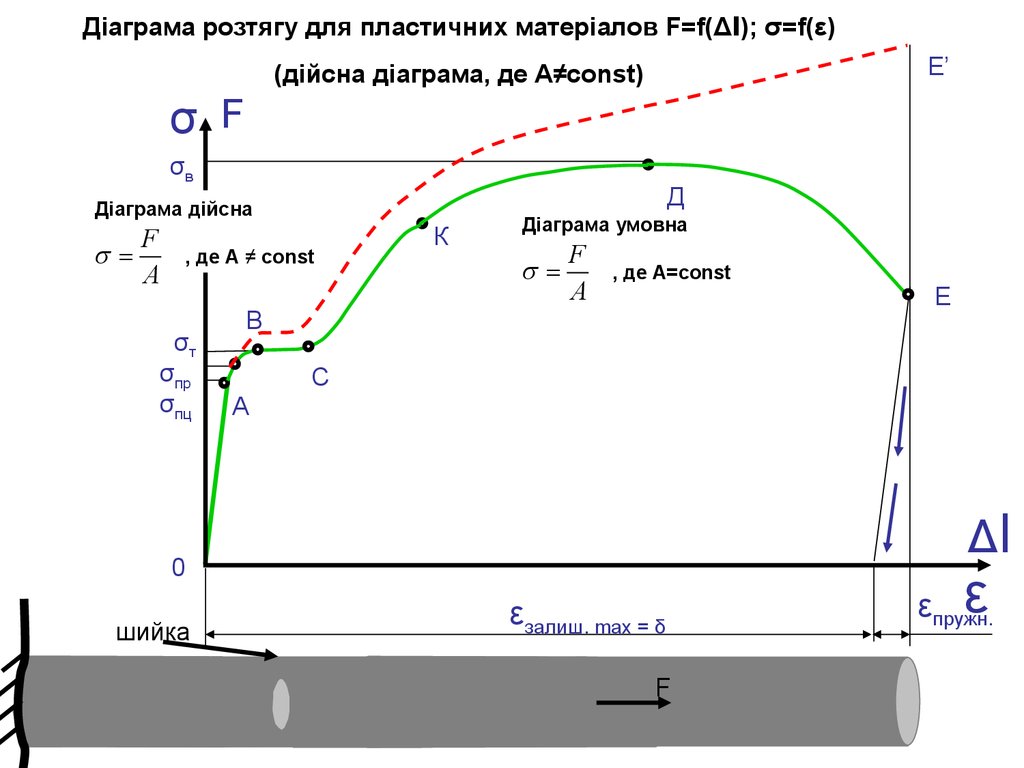
Дійсна межа міцності або дійсний опір розриву – напруження, що відповідає руйнуючій силі Fруйн,
обчислене для площі поперечного перерізу зразка в місці розриву A1 (для Ст3 σд =900-1000 МПа).
Оскільки на ділянці EK утворюється шийка і площа поперечного перерізу швидко зменшується,
напруження збільшується (EK1) при реєстрованому падінні зусилля.
Fруйн
д =
A1
.
Механізм руйнування: в області шийки утворюються дрібні поздовжні тріщини, які потім зливаються
в одну центральну тріщину, перпендикулярну осі розтягування, далі тріщина поширюється до
поверхні шийки, розвертаючись приблизно на 450, і при виході на поверхню утворює конічну частину
зламу. У результаті виходить поверхня зламу у вигляді "конуса" і "чашки". Стадія утворення конічної
поверхні показує, що матеріал на вершині тріщини починає руйнуватися за механізмом ковзання (по
майданчиках максимальних дотичних напружень), характерному для крихких матеріалів.
15.
Діаграма розтягу для пластичних матеріалов F=f(Δl); σ=f(ε)Е’
(дійсна діаграма, де А≠const)
σ F
σв
Д
Діаграма дійсна
F
=
A
, де A ≠ const
σт
σпр
σпц
Діаграма умовна
К
=
F
A
, де A=const
В
Е
С
А
Δl
0
εзалиш. max = δ
шийка
F FF F F
F
F
ε
εпружн.
16.
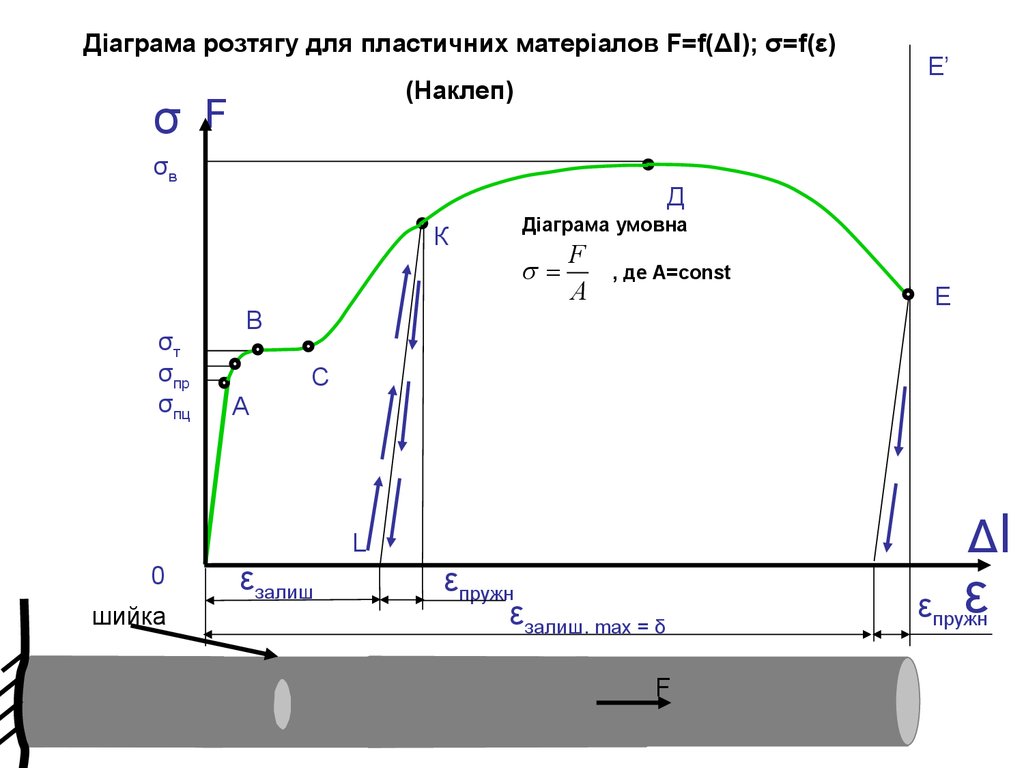
Діаграма розтягу для пластичних матеріалов F=f(Δl); σ=f(ε)(Наклеп)
σ F
σв
Д
К
Діаграма умовна
=
σт
σпр
σпц
F
A
, де A=const
В
шийка
Е
С
А
L
0
Е’
εзалиш
F FF F
εпружн
εзалиш. max = δ
F
F
F
Δl
ε
εпружн
17.
Діаграма стиску різних матеріалів – При стиску поводження матеріалу зразка відрізняється відйого поведінки при розтягуванні.
F
FТ
Fпц
B
A
l
O
F
Fmax
l
Діаграма маловуглецевої сталі – Початкова ділянка діаграми є
прямолінійним (до точки A) і збігається з аналогічною ділянкою
діаграми розтягування. Це свідчить про те, що модуль пружності
у сталі можна приймати однаковим при розтягуванні і
стиску. Нелінійна ділянка до площадки текучості також збігається
з подібною ділянкою на діаграмі розтягування. Значення межі
пропорційності і межі текучості при розтягуванні і стиску
практично однакові. Площадка текучості при стиску виражена
дуже слабо і після неї крива йде все більш круто вгору внаслідок
розвитку значних пластичних деформацій, що приводять до
збільшення площі поперечного перерізу. Зразок сплющується
приймаючи бочкоподібну форму. На цьому
випробування закінчують, тому що зразок зруйнувати не
вдасться, не вдається визначити і межу міцності.
Діаграма стиску чавуну – Початкова ділянка діаграми має майже лінійну
залежність, на цій ділянці форма і розміри зразка змінюються незначно.
При наближенні до максимального навантаження крива стає більш
пологою і зразок приймає трохи бочкоподібну форму. При досягненні
навантаженням найбільшого значення, з'являються тріщини під кутом
приблизно 450 і настає руйнування по майданчиках з найбільшими
дотичними напруженнями (крихке руйнування).
Інші крихкі матеріали (камінь, бетон) мають подібну діаграму і такий
характер руйнування. Крихкі матеріали працюють на стиск значно краще,
ніж на розтяг, наприклад, межа міцності сірого чавуну на стиск 560-900
МПа, а на розтяг - 120-190 МПа.
18.
■ Діаграма стиску деревини – деревина – анізотропний матеріал. Опір при стиску залежить відрозташування волокон щодо направлення стискаючої сили.
При стиску вздовж волокон на ділянці OA деревина працює майже пружно, деформації ростуть
пропорційно збільшенню стискаючої сили. Далі деформації починають рости швидше, ніж зусилля,
внаслідок виникнення пластичних деформацій в окремих волокнах. Руйнування відбувається при
максимальному навантаженні в результаті втрати місцевої стійкості ряду волокон, супроводжуваної
зрушенням з утворенням поздовжніх тріщин.
Fmax
F
A
O
B
l
При стиску деревини поперек волокон на ділянці OB деревина працює майже пружно, деформації
ростуть пропорційно збільшенню стискаючої сили. Далі деформації починають рости дуже швидко
при малому збільшенні сили, внаслідок ущільнення (спресовування) окремих волокон. При наявності
сучків і інших пороків (тріщин) зразок може зруйнуватися розколюванням. Руйнівне навантаження
визначається умовно при досягненні деформації стиснення при якій висота зразка зменшується на
третину вихідної висоти.
19.
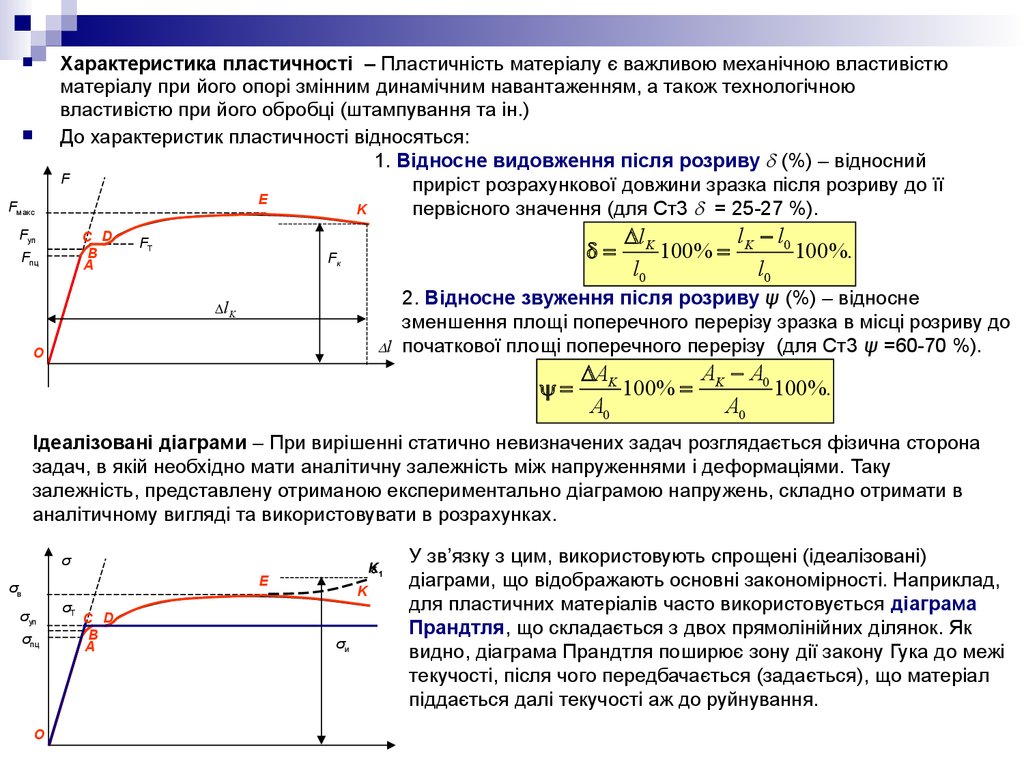
FмаксХарактеристика пластичності – Пластичність матеріалу є важливою механічною властивістю
матеріалу при його опорі змінним динамічним навантаженням, а також технологічною
властивістю при його обробці (штампування та ін.)
До характеристик пластичності відносяться:
1. Відносне видовження після розриву (%) – відносний
F
приріст розрахункової довжини зразка після розриву до її
E
K
первісного значення (для Ст3 = 25-27 %).
Fуп
С D
B
A
Fпц
FТ
=
Fк
l -l
lK
100% = K 0 100%.
l0
l0
2. Відносне звуження після розриву ψ (%) – відносне
зменшення площі поперечного перерізу зразка в місці розриву до
l початкової площі поперечного перерізу (для Ст3 ψ =60-70 %).
lK
O
y=
A - A0
AK
100% = K
100%.
A0
A0
Ідеалізовані діаграми – При вирішенні статично невизначених задач розглядається фізична сторона
задач, в якій необхідно мати аналітичну залежність між напруженнями і деформаціями. Таку
залежність, представлену отриманою експериментально діаграмою напружень, складно отримати в
аналітичному вигляді та використовувати в розрахунках.
σ
K
ε1
E
σв
σуп
σпц
O
σТ
С D
B
A
K
σи
У зв’язку з цим, використовують спрощені (ідеалізовані)
діаграми, що відображають основні закономірності. Наприклад,
для пластичних матеріалів часто використовується діаграма
Прандтля, що складається з двох прямолінійних ділянок. Як
видно, діаграма Прандтля поширює зону дії закону Гука до межі
текучості, після чого передбачається (задається), що матеріал
піддається далі текучості аж до руйнування.
20.
FE
Fмакс
Fуп
С D
B
A
Fпц
FТ
K
Fк
lK
l
O
l
d l
σ
K1
E
σв
σТ
σуп
σпц
С D
B
A
K
σи
O
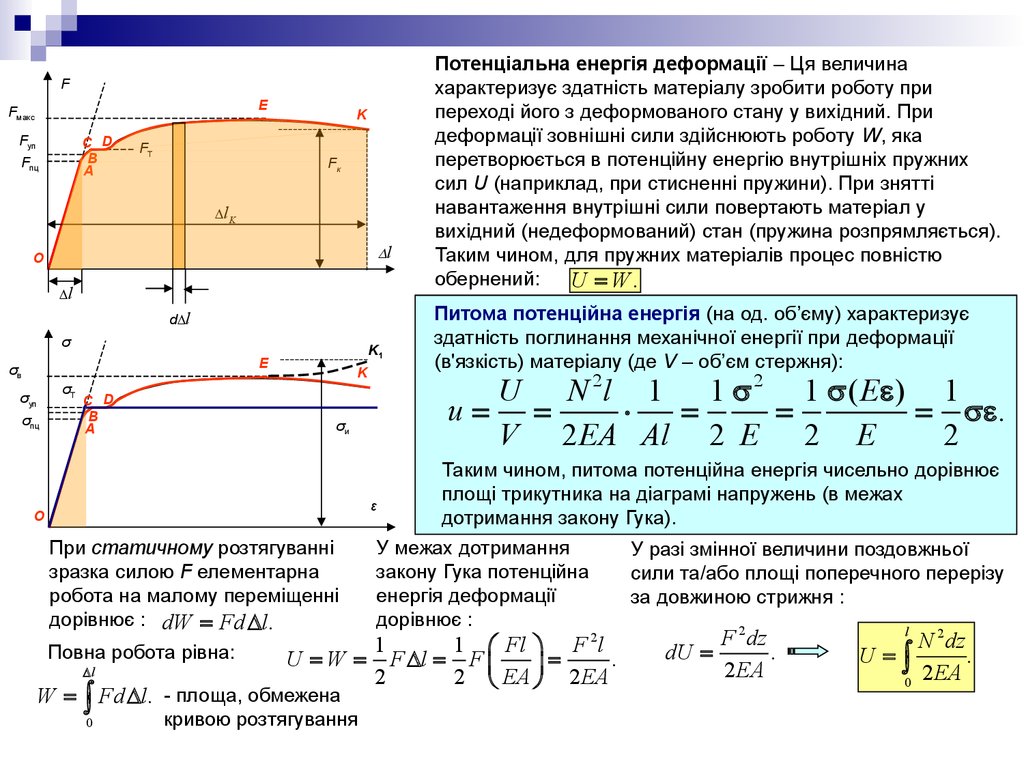
При статичному розтягуванні
зразка силою F елементарна
робота на малому переміщенні
дорівнює : dW = Fd l.
Повна робота рівна:
l
Питома потенційна енергія (на од. об’єму) характеризує
здатність поглинання механічної енергії при деформації
(в'язкість) матеріалу (де V – об’єм стержня):
U N 2l 1 1 2 1 ( E e ) 1
u= =
×
=
=
= e.
V 2 EA Al 2 E 2 E
2
Таким чином, питома потенційна енергія чисельно дорівнює
площі трикутника на діаграмі напружень (в межах
ε
дотримання закону Гука).
У межах дотримання
У разі змінної величини поздовжньої
закону Гука потенційна
сили та/або площі поперечного перерізу
енергія деформації
за довжиною стрижня :
дорівнює :
2
1
1 Fl F 2l
U = W = F l = F
.
=
2
2 EA 2 EA
W = Fd l. - площа, обмежена
0
Потенціальна енергія деформації – Ця величина
характеризує здатність матеріалу зробити роботу при
переході його з деформованого стану у вихідний. При
деформації зовнішні сили здійснюють роботу W, яка
перетворюється в потенційну енергію внутрішніх пружних
сил U (наприклад, при стисненні пружини). При знятті
навантаження внутрішні сили повертають матеріал у
вихідний (недеформований) стан (пружина розпрямляється).
Таким чином, для пружних матеріалів процес повністю
обернений:
U = W.
кривою розтягування
F dz
dU =
.
2 EA
l
U=
0
N 2 dz
.
2 EA
21. Додаткові питання
Поняття про повзучість та релаксацію – Багато будівельних конструкцій при експлуатації деформуються при тривалій дії постійнихнавантажень. Це обумовлюється здатністю матеріалів деформуватися в часі при дії постійних навантажень. Цей процес і названий
повзучістю. Повзучість притаманна таким матеріалам, як цегла, деревина, полімери, камінь, гума, ґрунти і т.п. Метали також виявляють
повзучість при високих температурах, а кольорові метали - і при звичайній (кімнатній) температурі. Повзучість може виникати і при малих
навантаженнях, які при короткочасній дії викликають тільки пружні деформації.
D
ε
εп
ε(0)
0
C
2
B
A
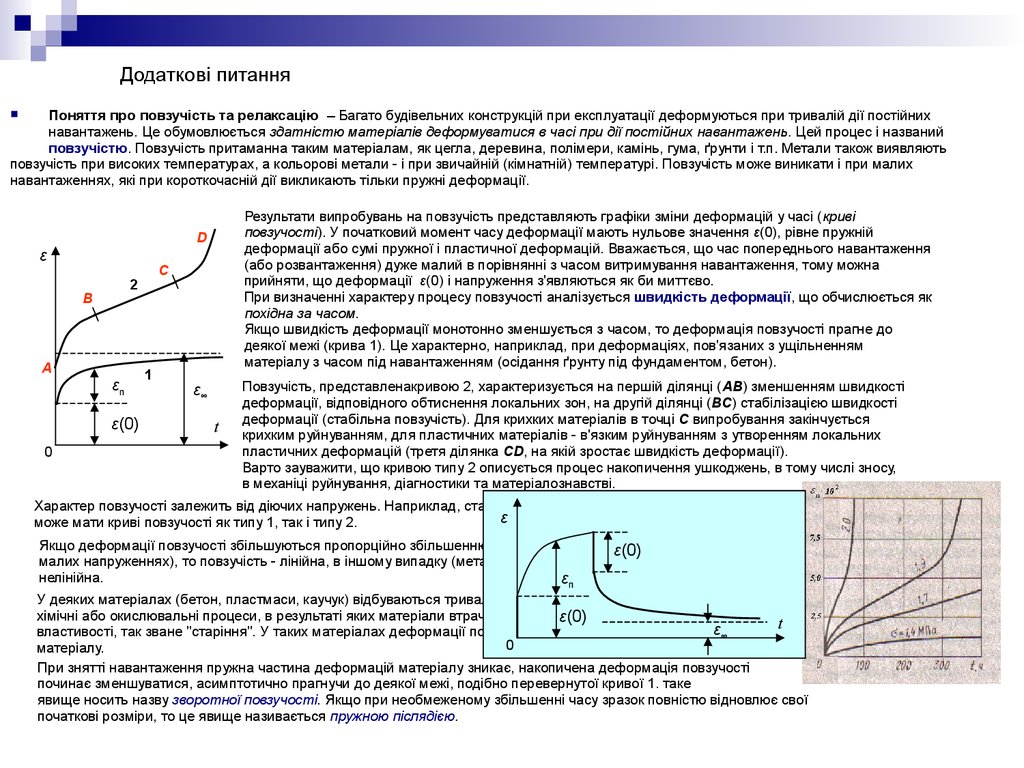
Результати випробувань на повзучість представляють графіки зміни деформацій у часі (криві
повзучості). У початковий момент часу деформації мають нульове значення ε(0), рівне пружній
деформації або сумі пружної і пластичної деформацій. Вважається, що час попереднього навантаження
(або розвантаження) дуже малий в порівнянні з часом витримування навантаження, тому можна
прийняти, що деформації ε(0) і напруження з'являються як би миттєво.
При визначенні характеру процесу повзучості аналізується швидкість деформації, що обчислюється як
похідна за часом.
Якщо швидкість деформації монотонно зменшується з часом, то деформація повзучості прагне до
деякої межі (крива 1). Це характерно, наприклад, при деформаціях, пов'язаних з ущільненням
матеріалу з часом під навантаженням (осідання ґрунту під фундаментом, бетон).
1
ε∞
t
Повзучість, представленакривою 2, характеризується на першій ділянці (AB) зменшенням швидкості
деформації, відповідного обтиснення локальних зон, на другій ділянці (BC) стабілізацією швидкості
деформації (стабільна повзучість). Для крихких матеріалів в точці C випробування закінчується
крихким руйнуванням, для пластичних матеріалів - в'язким руйнуванням з утворенням локальних
пластичних деформацій (третя ділянка CD, на якій зростає швидкість деформації).
Варто зауважити, що кривою типу 2 описується процес накопичення ушкоджень, в тому числі зносу,
в механіці руйнування, діагностики та матеріалознавстві.
Характер повзучості залежить від діючих напружень. Наприклад, сталь при різних рівнях напружень
ε
може мати криві повзучості як типу 1, так і типу 2.
Якщо деформації повзучості збільшуються пропорційно збільшенню напружень (бетон, ε(0)
пластмаса при
малих напруженнях), то повзучість - лінійна, в іншому випадку (метал при високих температурах) нелінійна.
εп
У деяких матеріалах (бетон, пластмаси, каучук) відбуваються тривалі, повільно протікаючі
хімічні або окислювальні процеси, в результаті яких матеріали втрачають свої первинні
ε(0)
ε∞
властивості, так зване "старіння". У таких матеріалах деформації повзучості звичайно залежать від "віку"
0
матеріалу.
t
При знятті навантаження пружна частина деформацій матеріалу зникає, накопичена деформація повзучості
починає зменшуватися, асимптотично прагнучи до деякої межі, подібно перевернутої кривої 1. таке
явище носить назву зворотної повзучості. Якщо при необмеженому збільшенні часу зразок повністю відновлює свої
початкові розміри, то це явище називається пружною післядією.
22.
Релаксація напружень – Якщо зразок витримується протягом деякого тривалого часу в стані, при якому деформація залишається постійною, тонапруження в матеріалі, що мали в початковий момент значення σ(0), понижуються асимптотично до деякого значення. Явище повільного
зменшення напружень у зразку при постійній деформації називається релаксацією.
Таким чином, явище релаксації в деякій мірі зворотне повзучості, але природа цих двох явищ одна енергія теплових пружних коливань атомів додається до енергії, яка забезпечується зовнішніми силами, що
викликають деформацію.
При вільній деформації під дією прикладених сил відбувається додатковий рух дислокацій (дислокаціїдефекти кристалічної решітки) і деформація зростає. Оскільки при звичайній температурі ця енергія
незначна, то повзучість (приріст деформацій) відбувається в цьому випадку повільно.
При постійній деформації надходження додаткової енергії теплових коливань атомів призводить до
перерозподілу дислокацій з частковим відновленням регулярності кристалічної решітки. При цьому енергія
деформації зменшується, що призводить до зменшення напружень, якщо деформація залишається
постійною.
σ
σ(0)
0
t
σ∞













 physics
physics








