Similar presentations:
Аеродинаміка та динаміка польоту літака. Характеристики профілю крила. Поздовжні аеродинамічні сили та момент. (Лекція 3.2.1)
1.
ЛЕКЦІЯ № 3з навчальної дисципліни
“Аеродинаміка та динаміка
польоту літака”
Змістовий модуль 2. Аеродинамічні
характеристики профілю крила.
Заняття 1.
Поздовжні аеродинамічні сили
та поздовжній момент.
1
2.
Навчальна та виховна мета: Вивчити геометричні параметри профілю,основні системи координат і сили, які в них визначаються.
Навчальні питання:
2.1 Основні геометричні параметри профілю крила.
Аеродинамічні профілі.
2.2. Швидкісна поточна та зв’язана системи
координат з профілем крила.
2.3. Способи створення підйомної сили. Картина
розподілу тиску по профілю крила.
2.4. Поздовжні аеродинамічні сили та поздовжній
момент.
Навчальна література:
1. Вотяков В. Д. Аэродинамика летательных аппаратов и гидравлика их систем. Ч. 1 /
В. Д. Вотяков. – М. : ВПИА им. проф. Н. Е. Жуковского, 1972. – С. 6...41.
3.
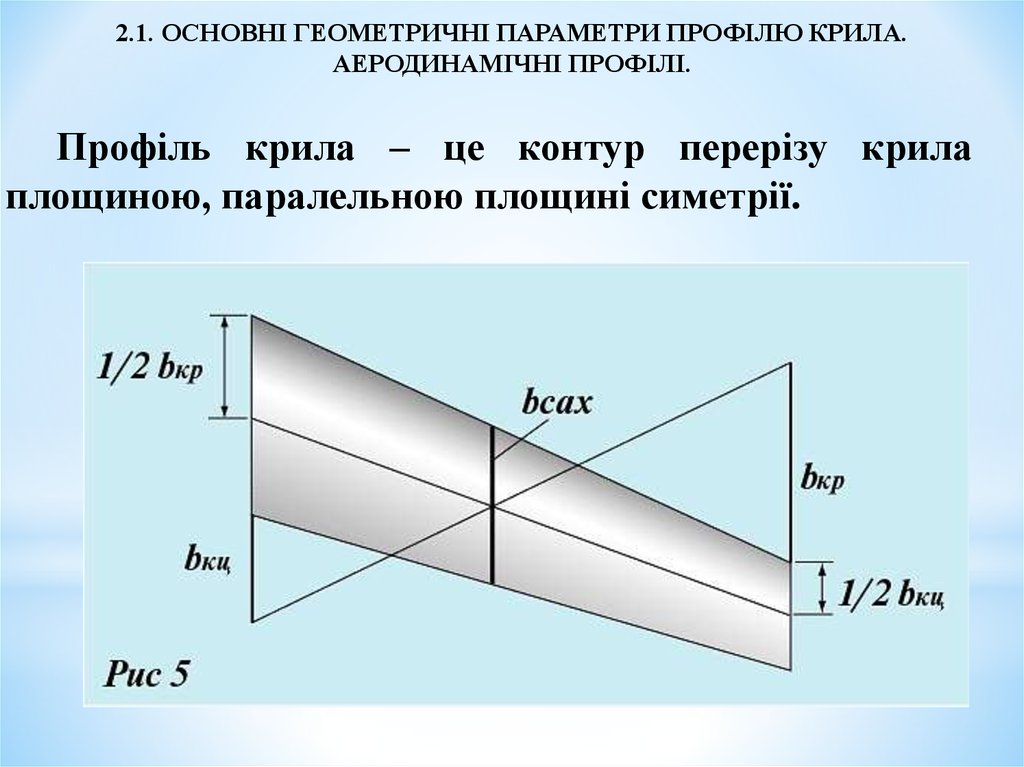
2.1. ОСНОВНІ ГЕОМЕТРИЧНІ ПАРАМЕТРИ ПРОФІЛЮ КРИЛА.АЕРОДИНАМІЧНІ ПРОФІЛІ.
Профіль крила – це контур перерізу крила
площиною, паралельною площині симетрії.
4.
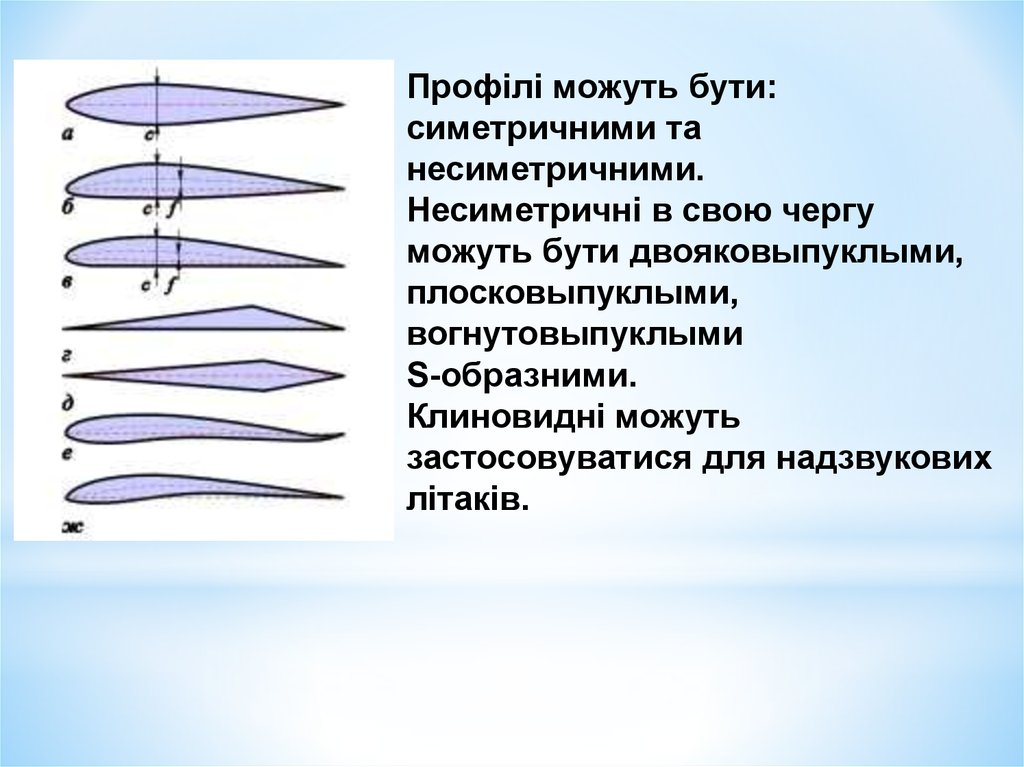
Профілі можуть бути:симетричними та
несиметричними.
Несиметричні в свою чергу
можуть бути двояковыпуклыми,
плосковыпуклыми,
вогнутовыпуклыми
S-образними.
Клиновидні можуть
застосовуватися для надзвукових
літаків.
5.
Розглянемо основні геометричні параметри профілю.А
А
y
по А A
0
Середня лінія
r
xc
cmax
yв
f max
xf
b
yн хорда
x
6.
yпо А A
0
Середня лінія
r
xc
cmax
yв
f max
xf
b
yн хорда
x
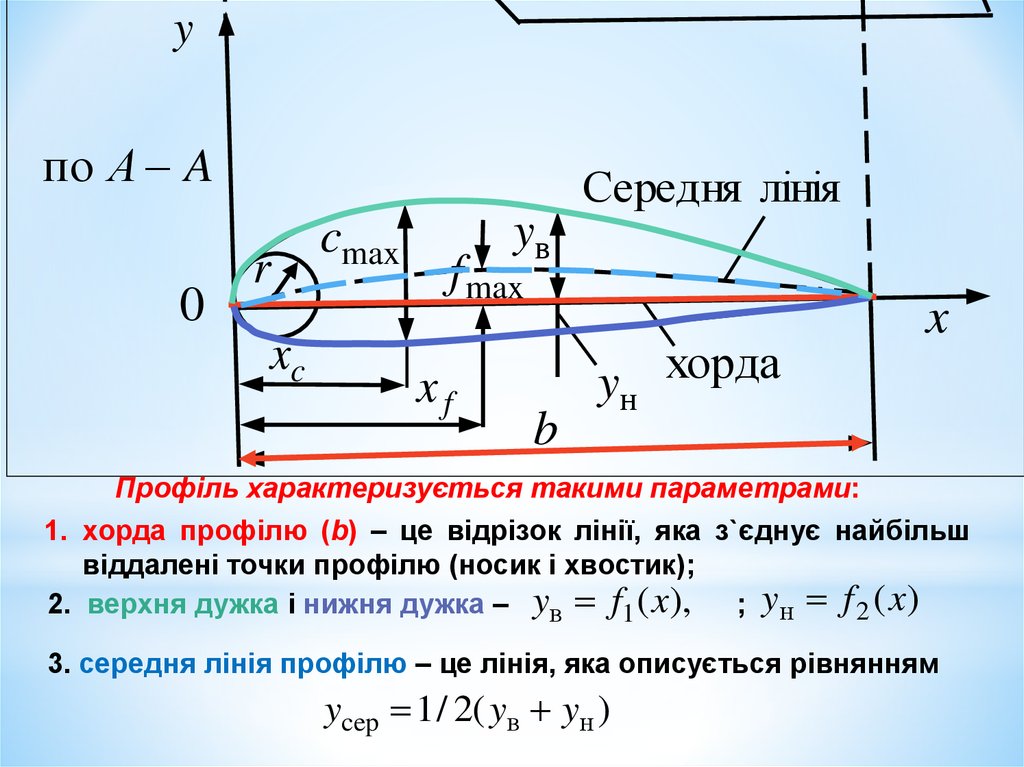
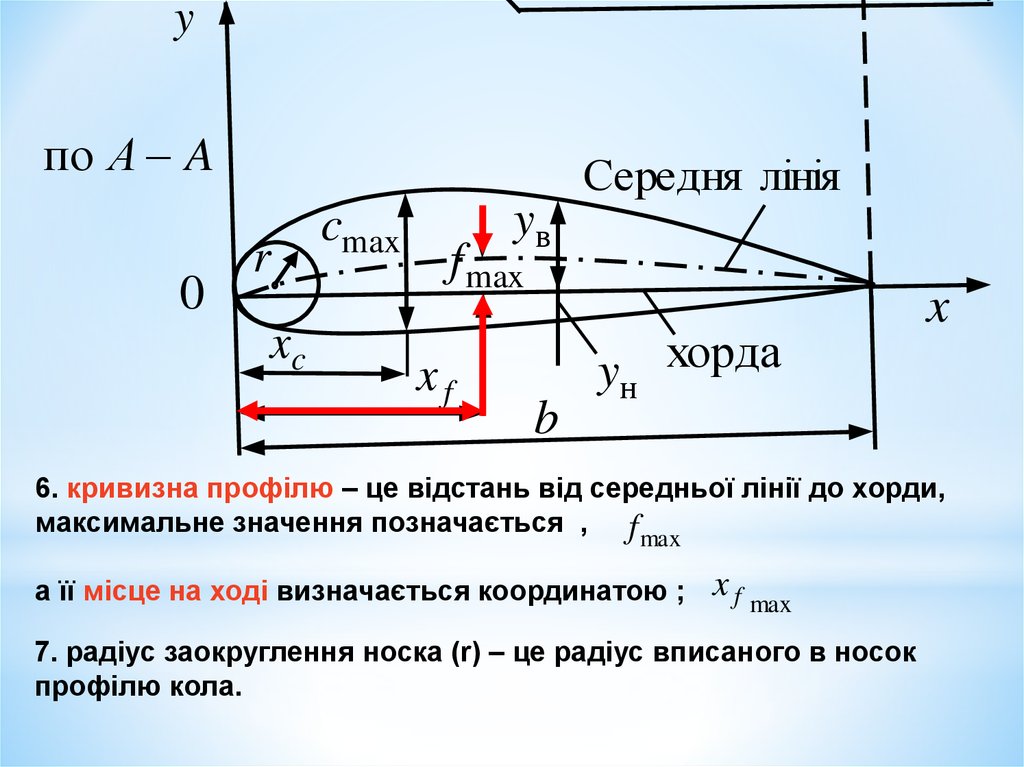
Профіль характеризується такими параметрами:
1. хорда профілю (b) – це відрізок лінії, яка з`єднує найбільш
віддалені точки профілю (носик і хвостик);
2. верхня дужка і нижня дужка – yв f1 ( x),
; yн f 2 ( x )
3. середня лінія профілю – це лінія, яка описується рівнянням
ycep 1 / 2( yв yн )
7.
yпо А A
0
Середня лінія
r
xc
cmax
yв
f max
xf
b
yн хорда
x
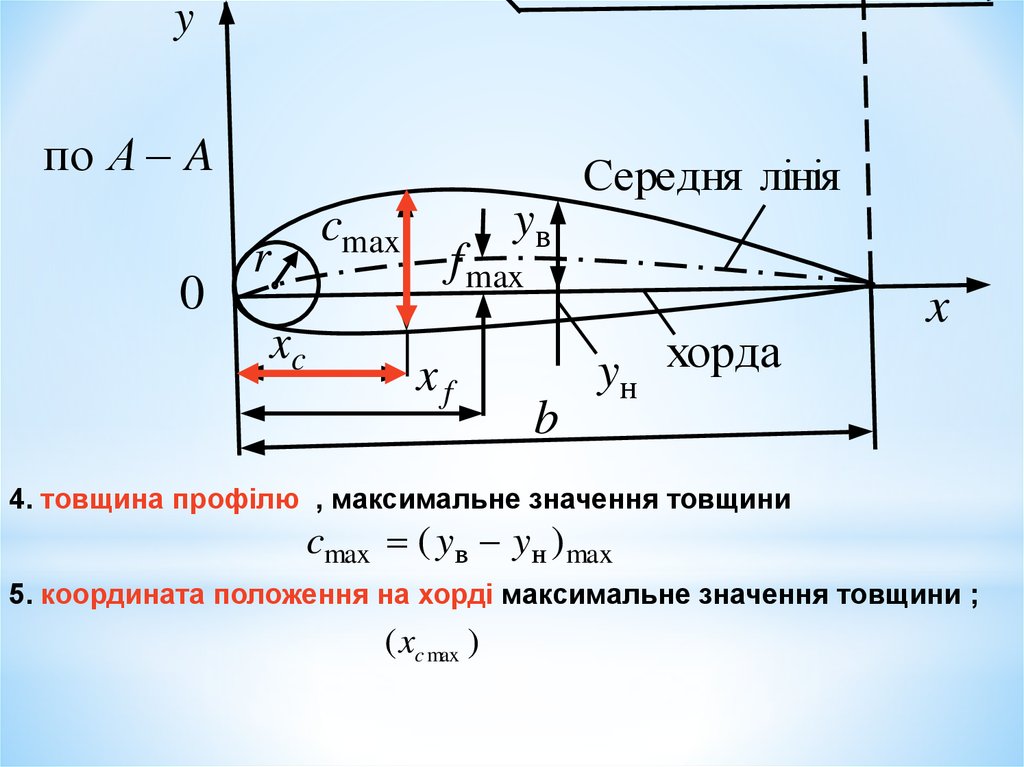
4. товщина профілю , максимальне значення товщини
cmax ( yв yн ) max
5. координата положення на хорді максимальне значення товщини ;
( xc max )
8.
yпо А A
0
Середня лінія
r
xc
cmax
yв
f max
xf
b
yн хорда
x
6. кривизна профілю – це відстань від середньої лінії до хорди,
максимальне значення позначається , f
max
а її місце на ході визначається координатою ;
x f max
7. радіус заокруглення носка (r) – це радіус вписаного в носок
профілю кола.
9.
2.1.1. Безрозмірні параметри профілюCmax
С
b
– відносна максимальна товщина ;
xc
xc
b
– відносна координата точки з максимальною
товщиною;
f
f
b
xf
xf
b
r
r
b
– відносна кривизна;
– відносна координата точки з максимальною
кривизною;
– відносний радіус заокруглення носка.
10.
2.2. ШВИДКІСНА ТА ЗВ’ЯЗАНА СИСТЕМИ КООРДИНАТЗ ПРОФІЛЕМ КРИЛА
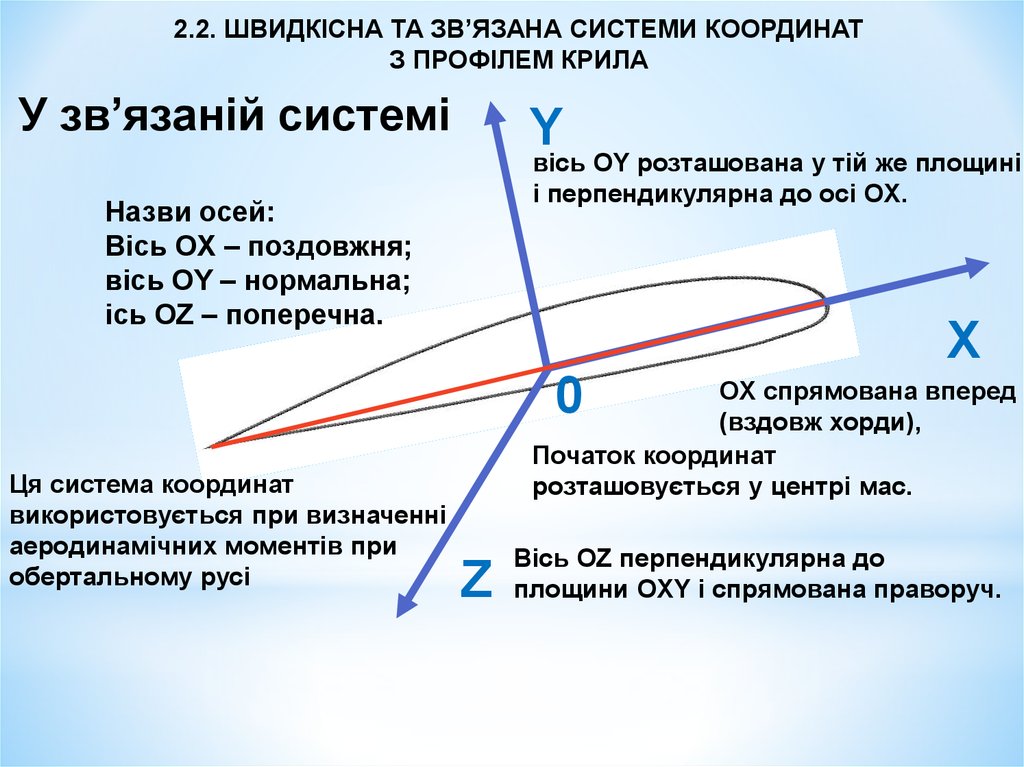
У зв’язаній системі
Y
вісь OY розташована у тій же площині
і перпендикулярна до осі OX.
Назви осей:
Вісь OX – поздовжня;
вісь OY – нормальна;
ісь OZ – поперечна.
X
0
Ця система координат
використовується при визначенні
аеродинамічних моментів при
обертальному русі
OХ спрямована вперед
(вздовж хорди),
Початок координат
розташовується у центрі мас.
Z
Вісь OZ перпендикулярна до
площини OXY і спрямована праворуч.
11.
2.2. ШВИДКІСНА ТА ЗВ’ЯЗАНА СИСТЕМИ КООРДИНАТЗ ПРОФІЛЕМ КРИЛА
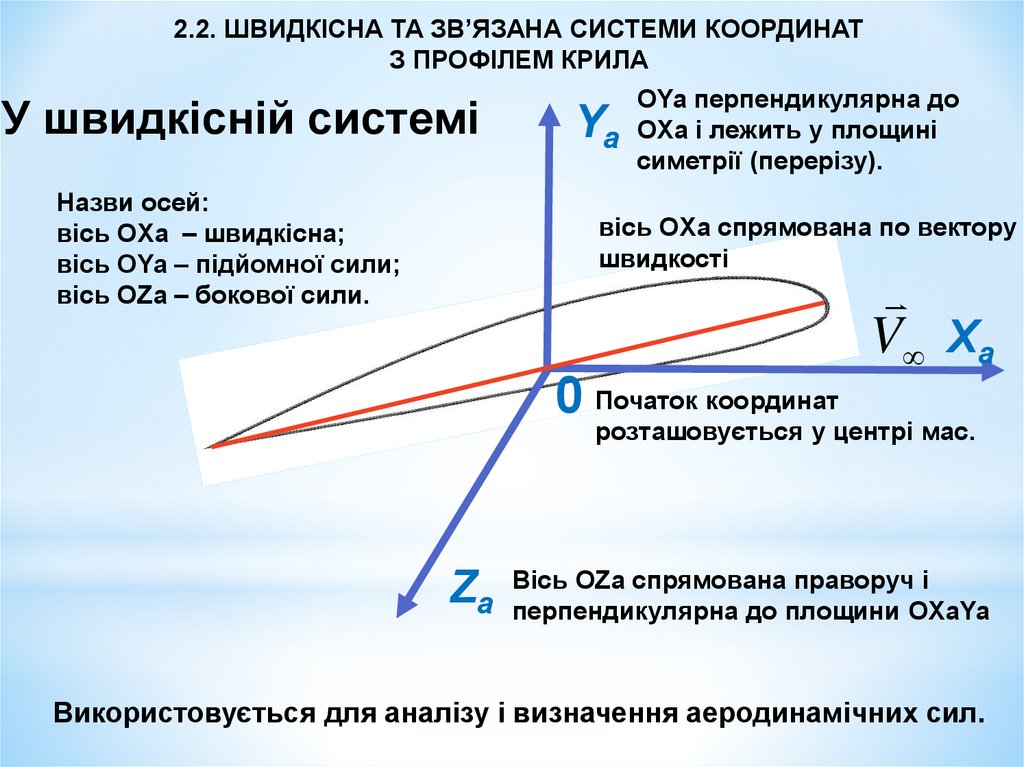
У швидкісній системі
Назви осей:
вісь OXa – швидкісна;
вісь OYa – підйомної сили;
вісь OZa – бокової сили.
OYa перпендикулярна до
a OХa і лежить у площині
симетрії (перерізу).
Y
вісь OXa спрямована по вектору
швидкості
V Xa
0 Початок координат
розташовується у центрі мас.
Za
Вісь OZa спрямована праворуч і
перпендикулярна до площини OXaYa
Використовується для аналізу і визначення аеродинамічних сил.
12.
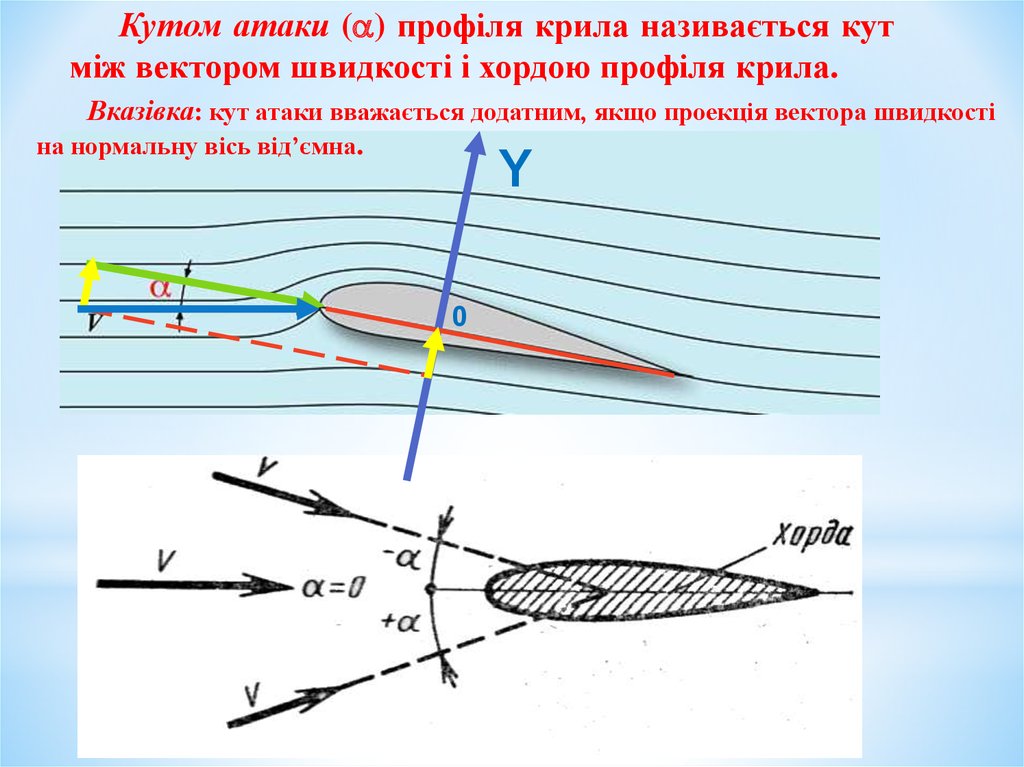
Кутом атаки ( ) профіля крила називається кутміж вектором швидкості і хордою профіля крила.
Вказівка: кут атаки вважається додатним, якщо проекція вектора швидкості
на нормальну вісь від’ємна.
Y
0
13.
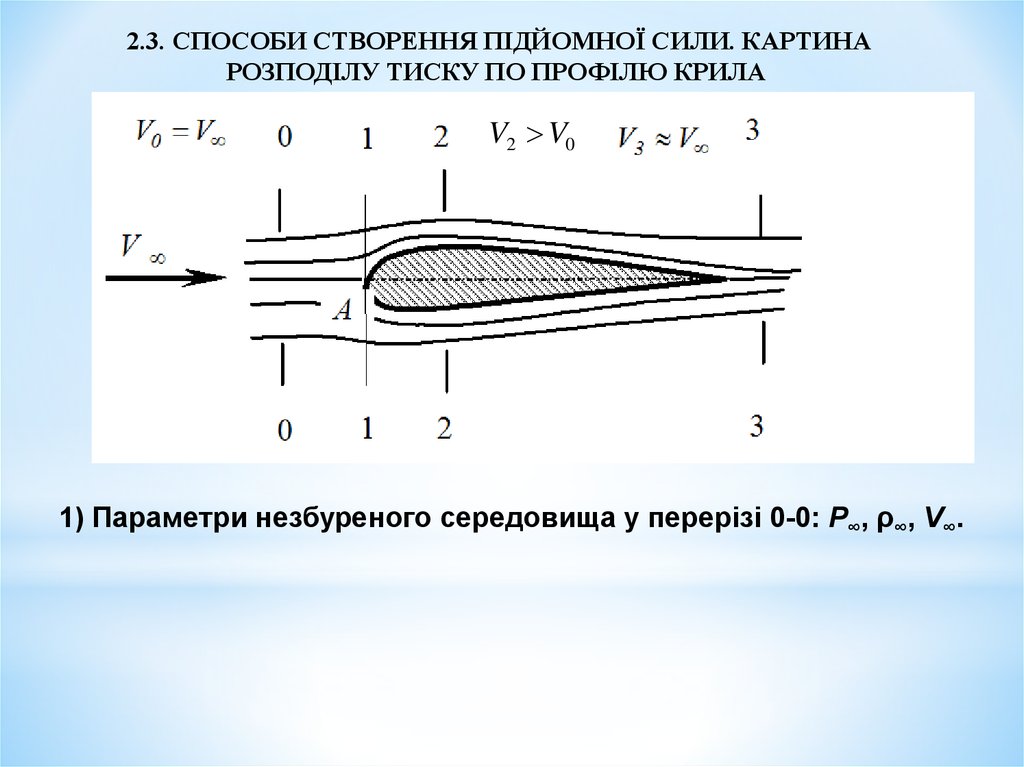
2.3. СПОСОБИ СТВОРЕННЯ ПІДЙОМНОЇ СИЛИ. КАРТИНАРОЗПОДІЛУ ТИСКУ ПО ПРОФІЛЮ КРИЛА
V2 V0
1) Параметри незбуреного середовища у перерізі 0-0: Р∞, ρ∞, V∞.
14.
V2 V02) В передній критичній точці (точка А в перерізі 1-1),
потік повністю гальмується, V1 0 швидкість дорівнює
нулю , а статичний тиск стає рівним повному тиску
незбуреного потоку P0 .
V 2
V12
P
P1
2
2
V1 0
P1 P0 P
V 2
2
15.
V2 V03) При обтіканні верхньої поверхні профілю площа перерізу струминки
спочатку зменшується до деякого мінімального значення (переріз 2-2),
швидкість повітря зростає згідно рівняння нерозривності:
V1 S1 V2 S 2
а статичний тиск падає згідно рівняння Бернуллі:
P1
V
2
1
2
P2
V
2
2
2
16.
V2 V04) Потім площа перерізу зростає (переріз 3–3), швидкість зменшується, а
статичний тиск зростає до значення, яке відповідає незбуреному потоку.
5) На нижній поверхні при додатному куті атаки, струминки мають меншу
деформацію, швидкість менша, ніж зверху, а тиск більший.
17.
Рис. 2.5. Векторна діаграма розподілу тискуЯкщо у масштабі побудувати вектори тисків по нормалі до поверхні крила,
одержимо картину розподілу тисків у даному перерізі
Сумарна різниця тиску на верхній і нижній поверхні створює підйомну
силу на профілі крила.
Y Рн Pв dS
S
Ya C ya
V
2
2
S
18.
На практиці розглядають не тиск, а коефіцієнт тиску.Коефіцієнт тиску – це зміна тиску у даній точці (Р) порівняно з
тиском незбуреного потоку (Р ), віднесена до динамічного тиску
(швидкісного напору):
P P
Сp
q
q
V 2
2
Інші форми запису коефіцієнта тиску:
V
C p 1
V
2
або, використовуючи рівняння нерозривності
V∞S∞ = V2S2, можемо записати::
S
C p 1
S2
0,7 PH M 2
– швидкісний напір
(динамічний тиск)
СР
1
0
СР В
СР Н
x
1
2
Рис.2.7. Епюра розподілу тиску
для несиметричного профілю
19.
2.4. ПОЗДОВЖНІ АЕРОДИНАМІЧНІ СИЛИ ТА ПОЗДОВЖНІЙ МОМЕНТ2.4.1. Коефіцієнти поздовжніх аеродинамічних сил та моменту
Аеродинамічними силами називаються сили, які
виникають внаслідок механічної взаємодії рухомих тіл з
повітрям.
Під час руху тіла на кожний його елемент діють
нормальні сили тиску (Р) і дотичні (тангенціальні) сили
тертя (F).
V
Fтер
Р
20.
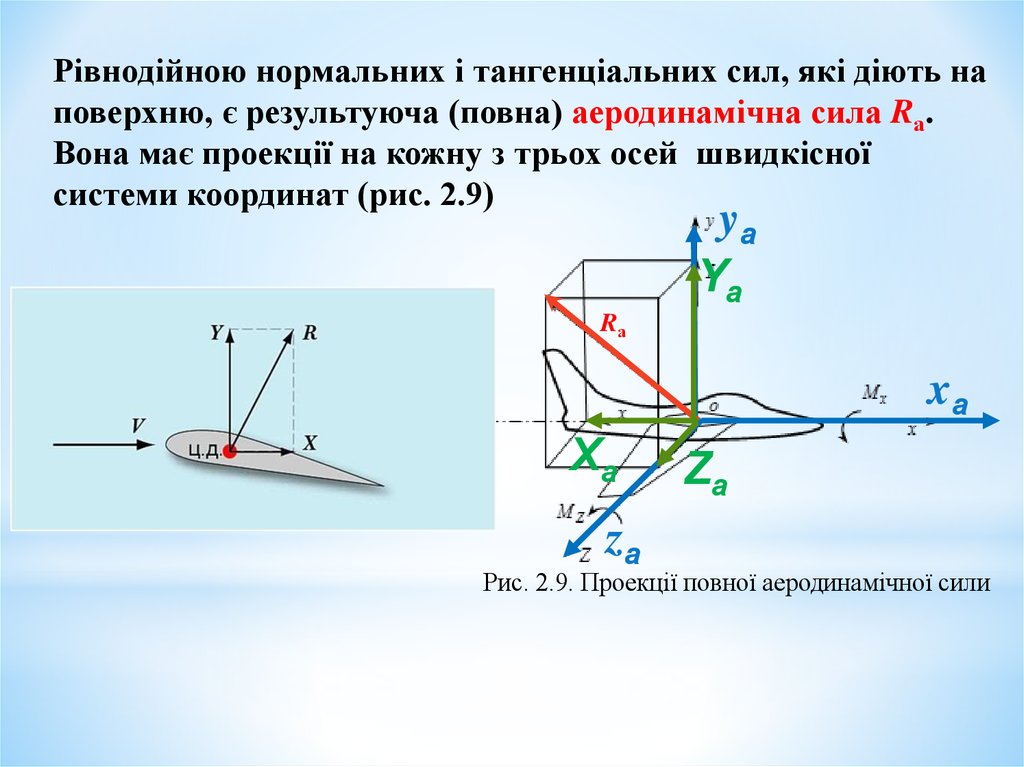
Рівнодійною нормальних і тангенціальних сил, які діють наповерхню, є результуюча (повна) аеродинамічна сила Rа.
Вона має проекції на кожну з трьох осей швидкісної
системи координат (рис. 2.9)
ya
Ya
Rа
xa
Xa
za
Za
Рис. 2.9. Проекції повної аеродинамічної сили
21.
yY
R
x
X
Z
z
Проекції аеродинамічної сили R
на осі зв`язаної системи координат
називають:
Х –поздовжня сила,
Y – нормальна сила,
Z – поперечна сила.
22.
yaYa
Ra
Xa
Za
za
V
xa
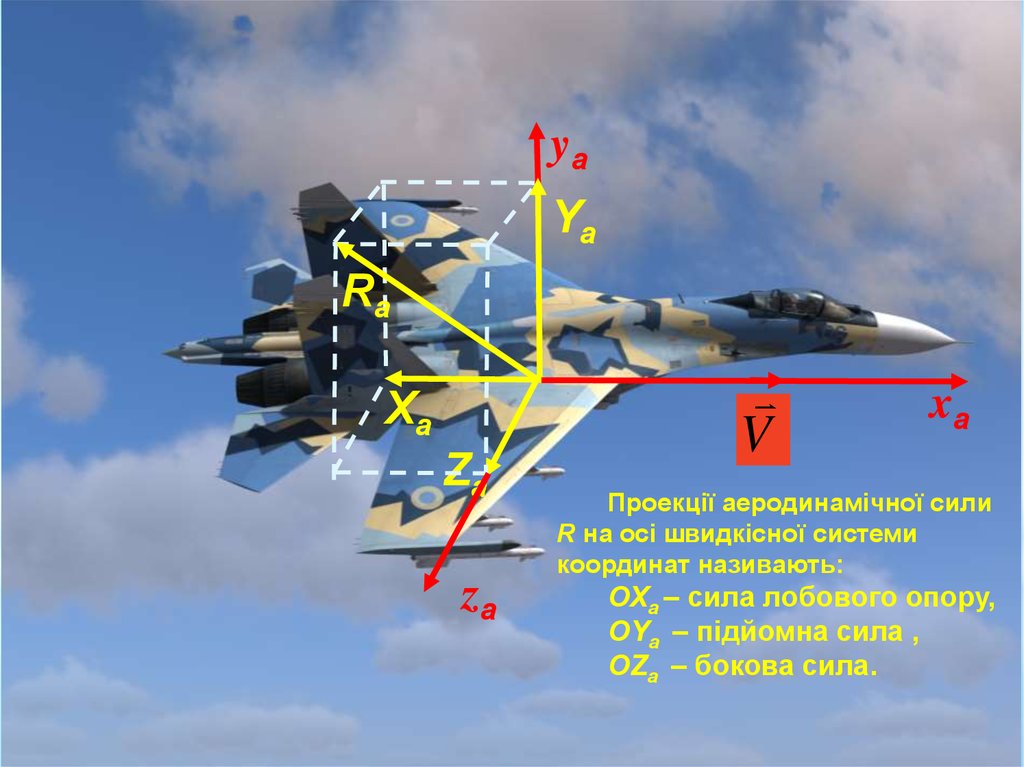
Проекції аеродинамічної сили
R на осі швидкісної системи
координат називають:
ОХа – сила лобового опору,
ОYа – підйомна сила ,
ОZа – бокова сила.
23.
Ya C yaX a C xa
Z a C za
V
2
V
2
Проекції аеродинамічної
S сили R на осі швидкісної
2
системи координат називають:
ОYа – підйомна сила ,
2
V
S ОХа – сила лобового опору,
2
ОZа – бокова сила.
2
S
24.
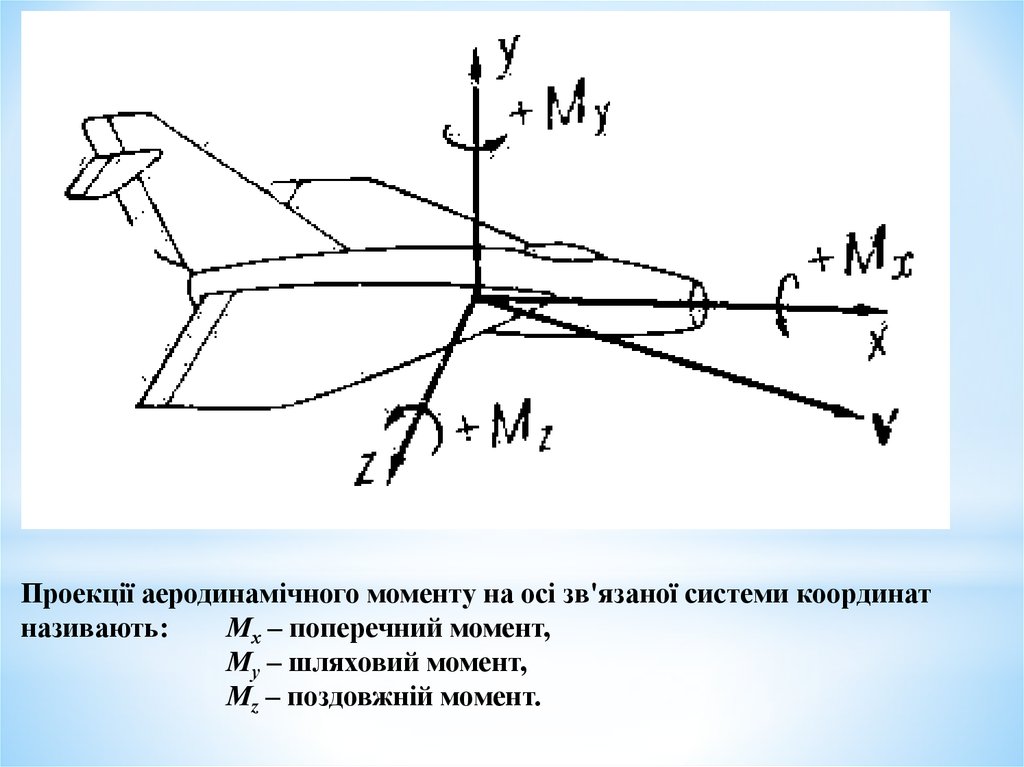
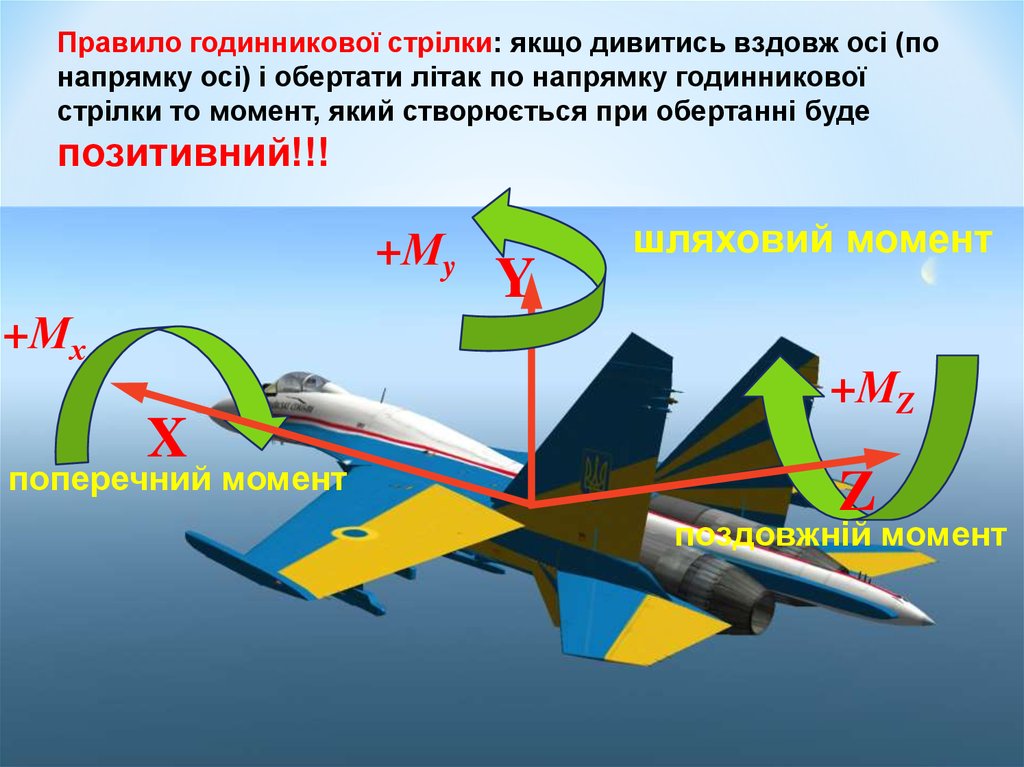
Проекції аеродинамічного моменту на осі зв'язаної системи координатназивають:
Мх – поперечний момент,
Му – шляховий момент,
Мz – поздовжній момент.
25.
Правило годинникової стрілки: якщо дивитись вздовж осі (понапрямку осі) і обертати літак по напрямку годинникової
стрілки то момент, який створюється при обертанні буде
позитивний!!!
+Мy
Y
шляховий момент
+Мх
X
поперечний момент
+МZ
Z
поздовжній момент
26.
M х mх qSкр l mхV 2
2
Sкр l mx 0,7 PH M 2 Sкр l
поперечний момент
+Мх
27.
M z mz qSкр ba mzV 2
2
Sкр ba mz 0,7 PH M 2 Sкр ba
поздовжній момент
+МZ
28.
+Мyшляховий момент
M y my qSкр l my
V 2
2
Sкр l my 0,7 PH M 2 Sкр l
29.
2.4.2. Коефіцієнти аеродинамічних силКоефіцієнтом аеродинамічної сили називається
безрозмірна величина, яка дорівнює відношенню
величини цієї сили до добутку швидкісного напору
q
V 2
2
0,7 PH M 2
і характерної площі S.
R
CR
q S
30.
Узв’язаній
системі
координат
коефіцієнти
аеродинамічних сил виражаються таким чином і мають
відповідно назви:
X
Y
Z
Cx
; Cy
; Cz
q S
q S
q S
С x – коефіцієнт поздовжньої сили;
Сy
– коефіцієнт нормальної сили;
Сz
– коефіцієнт поперечної сили.
2X
2Y
Cx
; Cy
;
2
2
V S
V S
2Z
Cz
2
V S
31.
У швидкісній системі координат коефіцієнтиаеродинамічних сил виражаються таким чином і
мають відповідно назви:
Cx a
Xa
Ya
; Cya
;
q S
q S
Cz a
Сx a
– коефіцієнт лобового опору;
Сya
– коефіцієнт підйомної сили;
Сz a
– коефіцієнт бокової сили.
Cx a
2X a
2Ya
; Cy a
;
2
2
V S
V S
Cz a
Za
q S
2Z a
2
V S
32.
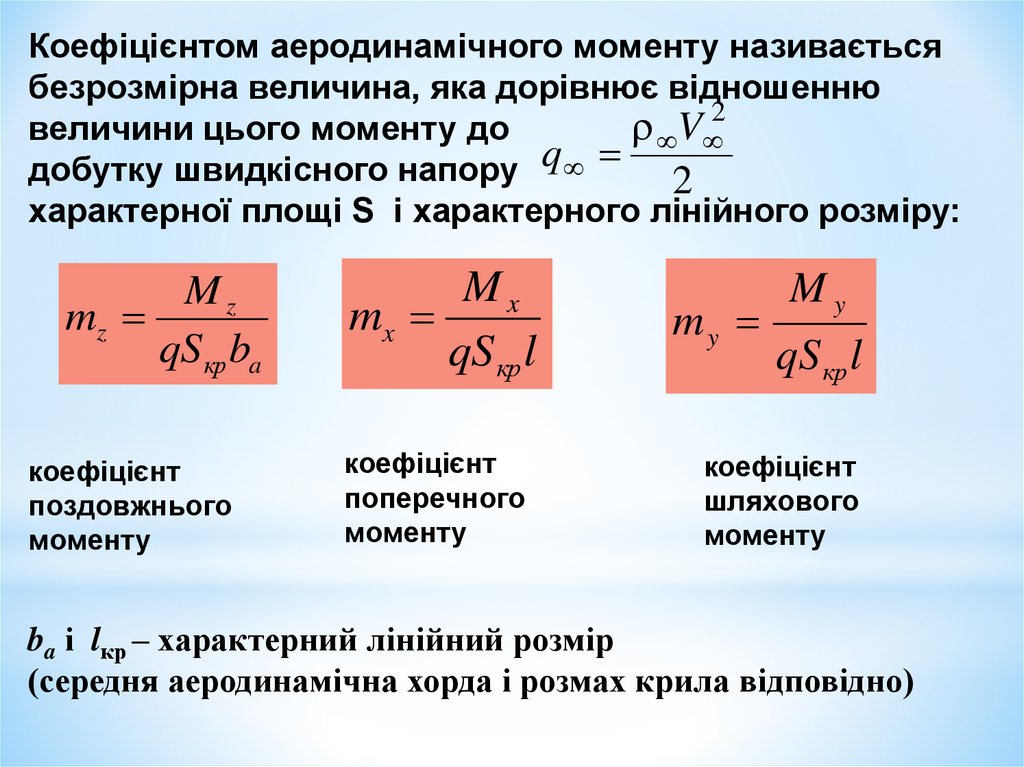
Коефіцієнтом аеродинамічного моменту називаєтьсябезрозмірна величина, яка дорівнює відношенню
V 2
величини цього моменту до
добутку швидкісного напору q 2
характерної площі S і характерного лінійного розміру:
Mz
mz
qSкр ba
коефіцієнт
поздовжнього
моменту
Mx
mx
qS кр l
коефіцієнт
поперечного
моменту
my
My
qS кр l
коефіцієнт
шляхового
моменту
ba і lкр – характерний лінійний розмір
(середня аеродинамічна хорда і розмах крила відповідно)


















 physics
physics








