Кінематика та динаміка обертального руху. Тема 3

1. Презентації до курсу лекцій

1

2. Тема 3.  Кінематика та динаміка обертального руху

Тема 3. Кінематика та
динаміка обертального руху
Питання за темою.
Обертальній рух абсолютно твердого тіла. Елементи
кінематики обертального руху: вектор елементарного кута
повороту тіла, кутова швидкість та кутове прискорення.
Зв'язок поміж лінійними та кутовими швидкостями і
прискореннями точок тіла, що обертається.
Момент імпульсу матеріальної точки відносно нерухомої
точки. Момент сили відносного відносно нерухомої точки.
Рівняння моментів. Момент імпульсу системи матеріальних
точок та твердого тіла відносно нерухомої осі обертання. .
Основне рівняння динаміки обертального руху твердого.
Момент інерції точки, системи матеріальних точок та тіла
відносно осі обертання. Моменти інерції тіл простої форми
(кільця, диску та стрижня). Теорема Штейнера. Закон
збереження моменту імпульсу та його зв'язок з ізотропністю
простору.
2

3. Елементи кінематики обертального руху

Лондонське
око (London
Eye) –
головне
колесо
огляду у
Лондоні
заввишки
135 метрів.
Повний
оберт робить
приблизно за
30 хвилин
Обертальний рух – це рух, при якому
всі точки тіла описують кола, центри
яких знаходяться на одній прямій,
перпендикулярній площинам, у яких
розташовані ці кола. Пряма зветься
віссю обертання.
При обертальному русі а.т.т. усі
точки тіла за однакові проміжки
часу повертаються на
однаковий кут. Цей кут є
величиною, що характеризує
обертальний рух всього тіла в
цілому.
Однак, для забезпечення
однозначності інформації про
рух тіла, а саме його
обертання, необхідно
додатково вказати вісь,
відносно якої відбувається
обертання, та напрямок, у
якому це обертання
відбувається.
3

4. Вектор елементарного кута повороту тіла

Вісь обертання та напрямок
повороту тіла можна задати
за допомогою вектора.
Модуль вектора елементарного кутового
переміщення дорівнює елементарному
куту, на який повернулося тіло.
Кутове переміщення (кут повороту) у СІ
d
вимірюється у радіанах (рад).
Кутове та лінійне переміщення точки
пов'язані між собою.
Точка А рухається дугою кола радіуса R.
А2 dr
d
Дуга лежить у площині, перпендикулярна
А
1
до осі обертання, а центром дуги
О1
(центром кола) є точка О1.
зауваження
d
Вектор елементарного кутового
dr 2 R sin
|
| Rd
d 0,sin d d
2
переміщення розташовано вздовж
осі обертання (аксіальний вектор). Або у векторній формі
Напрямок вектора визначається
dr d ; R
за правилом правого гвинта
R
4

5. Кутова швидкість та кутове прискорення

Для характеристики швидкості зміни
положення тіла при обертальному русі
(швидкості його обертання) вводять
кінематичну характеристику – кутову
швидкість.
d
dt
Кутова швидкість теж
аксіальний вектор,
спрямований вздовж осі
обертання
Якщо під час обертального руху тіла його швидкість
змінюється, то вводять кінематичну характеристику –
кутове прискорення.
d Структура кутових кінематичних характеристик
виявляється такою самою, як і лінійних
dt
5

6. Зв'язок поміж лінійною та кутовою швидкостями

При обертальному русі абсолютно твердого
тіла всі точки тіла мають однакову кутову
швидкість, а лінійна швидкість точок
залежить ще й від їхньої відстані до осі
обертання.
v
Характер руху
Рівномірний рух
Рівномірно
змінний рух
dr d d
;
dt
dt
dt
Поступальний рух
v const
S vt ;
x x0 v xt
a const
v v0 at ;
at 2
at 2
S v 0t
; x x0 v0t
2
2
v R
Обертальний рух
const
t N
t t
2 2
const
0 t ;
t2
1 t2
0 0t
; N 0t
2
2 2
6

7. Зв'язок поміж швидкостями та прискореннями

Для прискорень зв'язки виявляються більш складними
О1
R
v
dr d d
v
;
v R
dt
dt
dt
dv d
d
d
a
,
dt dt
dt
dt
v a an n
v an
R
a R
v
a
О1
an
v
a
v2
an v
2 R
R
Використання зв'язків поміж лінійними
та кутовими характеристиками
обертального руху дозволяє суттєво
спростити вирішення задач
7

8. Момент імпульсу матеріальної точки

Lz
L
L r;
L r p
L p.
О
r
О1
Мірою кількості механічного руху
матеріальної точки відносно деякого центру
О є момент імпульсу, який дорівнює
R
L
p
векторному добутку радіуса-вектора
матеріальної точки відносно центру О на
її імпульс.
Зазвичай, фізична величина момент
імпульсу використовується при
розгляданні й аналізі обертального руху.
Якщо через точку О проходить вісь (Z), то проекція Lz (див. рисунок)
– є момент імпульсу точки відносно цієї осі.
Величину Lz можна визначити ще так
Lz pR
8

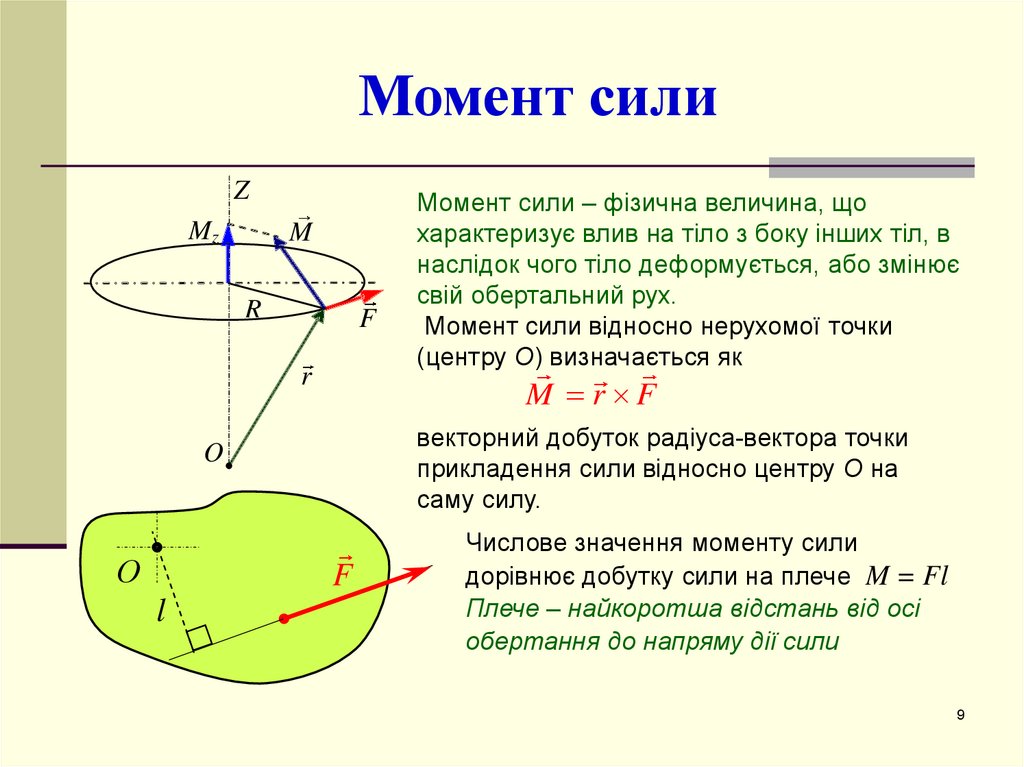
9. Момент сили

Z
Mz
M
R
F
r
M r F
векторний добуток радіуса-вектора точки
прикладення сили відносно центру О на
саму силу.
O
О
F
l
Момент сили – фізична величина, що
характеризує влив на тіло з боку інших тіл, в
наслідок чого тіло деформується, або змінює
свій обертальний рух.
Момент сили відносно нерухомої точки
(центру О) визначається як
Числове значення моменту сили
дорівнює добутку сили на плече M = Fl
Плече – найкоротша відстань від осі
обертання до напряму дії сили
9

10. Рівняння моментів

З'ясуємо, чим визначається швидкість зміни моменту імпульсу
dL d
dr
dp
r , p p r
v p r F
dt dt
dt
dt
v p m v v 0;
r F M
dL
M
dt
Таким чином швидкість зміни моменту імпульсу визначається
величиною і напрямком моменту сил, що діють на точку
відносно полюсу обертання.
Це співвідношення отримало назву «Рівняння моментів», і воно
є основним рівнянням динаміки обертального руху точки.
10

11. Момент імпульсу системи матеріальних точок

Для опису системи матеріальних
точок, які можуть здійснювати
обертальний рух можна записати
dL1
M 1 M 12 M 13 ...
dt
dL2
M 2 M 21 M 23 ...
dt
__ у сумі враховано M 12 M 21 0, ...
dLi
i dt i M i
Останнє рівняння є основним
рівнянням обертального руху для
системи матеріальних точок.
У системі тіл сума моментів усіх
внутрішніх сил дорівнює нулю,
так само, як і сума усіх
внутрішніх сил дорівнює нулю
Якщо система точок являє
собою абсолютно тверде тіло, і
воно обертається відносно
закріпленої осі Z, то рівняння
динаміки для опису такого руху
має вигляд
dLz
M iz
dt
i
11

12. Момент інерції точки та системи матеріальних точок

Момент імпульсу матеріальної точки, що обертається відносно деякої
нерухомої осі дорівнює
Lz p R mv R;
v z R ;
Lz mR 2 z
Співставлення цього співвідношення з формулою імпульсу точки дає
Кількість p mv Імпульс тіла
руху
L mR 2 Момент імпульсу
Мірою інертності точки при обертальному русі є величина mR2, яка
отримала назву момент інерції. Момент інерції (І) адитивна фізична
величина. Момент інерції системи точок дорівнює сумі моментів інерції
усіх точок, що складають систему.
Момент інерції абсолютно твердого тіла відносно обраної вісі
N
залежить не тільки від маси тіла, але й від того, як
2
ця маса розподілена по відношенню до осі
I mi ri
обертання.
i 1
12

13. Моменти інерції тіл простої форми

Теоретичне визначення моментів інерції тіл здійснюється з урахуванням
значення моменту інерції матеріальної точки та адитивності моменту
інерції системи точок.
Момент інерції тонкостінного циліндру (кільця)
m
R
I r 2 dm R 2 dm mR 2
dm
m
h
R
m
m
Момент інерції суцільного циліндру (диску)
dm
r
I mi ri 2
i
тіло
R
dI r 2dm r r 2 dV
m
4
2
V
R
mR
I 2 h r dr 2 h
.
4
2
l/2
0
3
– l/2
O
x
dm
dx
Момент інерції однорідного стрижня відносно цм
l /2
l /2
3
2
2
l
ml
I x 2 dV x 2 Sdx S x 2 dx S
3 8 12 13
V
l /2
l / 2

14. Теорема Штейнера.

Момент інерції тіла відносно довільної осі
що не проходить через центр мас (інерції)
чисельно дорівнює сумі моменту інерції
тіла відносно осі, що проходить через
центр мас паралельно даній осі та добутку
маси тіла на квадрат відстані між осями.
ri R0 r0i
О (ц.і.)
r0i
R0
О’
ri
mi
I I 0 M T R02
I mi ri 2 mi ri ri mi roi R0 roi R0
i
i
i
mi r0i 2 mi r0i R0 mi R02
i
i
i
I 0 2 R0 mi r0i mi R02 I 0 R 2 0 mi 2 R0 mi r0i
i
I 0 R 0 M T 2 R0
2
i
m
mr
m
i
i
i 0i
i
i
i
i
i
I 0 M T R 2 0 2 R0 rco mi ;
i
14

15. Закон збереження моменту імпульсу

Із рівняння, отриманого для опису
системи точок, які беруть участь в
обертальному русі
dLi
i dt i M i
випливає, що у замкненій системі
точок сума моментів імпульсів всіх
точок не змінюється з плином часу
dLi
d
i dt 0; dt i Li 0;
L const.
i
i
З проявами закону наочно
стикаємося у акробатиці, фігурному
катанні тощо.
15

16.

[email protected]
16