Курс загальної фізики. Лекція 2. Динаміка матеріальної точки і системи матеріальних точок динаміка обертального руху

1. Курс загальної фізики

КУРС
ЗАГАЛЬНОЇ
ФІЗИКИ
ЛЕКЦІЯ 2
ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ І СИСТЕМИ МАТЕРІАЛЬНИХ
ТОЧОК
ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

2. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
В основі класичної механіки лежать закони Ньютона, перетворення
Галілея, положення про існування інерційних систем відліку. Важливо
відзначити, що класична механіка не "працює" в наступних випадках:
1. при описі властивостей мікрочастинок (атомні та субатомні частинки);
2.
при
швидкостях,
близьких
до
швидкості
світла;
3. неефективна при розгляді систем з великим числом частинок.
Т.ч., класична механіка застосовна для тіл великої маси (в порівнянні з
масою атомів), які рухаються з малими швидкостями (в порівнянні зі
швидкістю світла).

3. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
I закон Ньютона
Існують такі системи відліку, щодо яких тіло (матеріальна
точка) за відсутності на нього зовнішніх впливів (або при їх
взаємної компенсації) зберігає стан спокою або рівномірного
прямолінійного руху.
Системи відліку, в яких виконується перший закон Ньютона,
називаються інерційними. З високим ступенем точності інерційною
системою вважається система відліку, пов'язана з Сонцем
(геліоцентрична). Земля рухається відносно Сонця з прискоренням,
але прискорення це настільки мале, що у більшості випадків її можна
вважати практично інерційною.

4. Динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
II закон Ньютона
Прискорення всякого тіла прямо пропорційно діючої на нього
силі і обернено пропорційно масі тіла.
- найбільш відома 2
d r
m a F или m 2 F
dt
форма записи II закону Ньютона, що припускає що маса тіла є
константа.
- універсальна форма записи
dp
dt
F
II закону Ньютона

5. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
тут m - маса тіла (м.т.); F- сила, яка діє на тіло (м.т); p -імпульс
тіла (м.т.).
маса тіла (м.т.) - це міра інертності тіла (м.т.) при
поступальному русі. інертність - властивість тіла, що полягає в
тому, що для зміни швидкості тіла відносно інерціальної системи
відліку необхідний вплив.
сила - це міра механічної взаємодії тіл.
імпульс - це міра механічного руху, векторна величина, що
дорівнює добутку маси тіла (м.т.) на його швидкість і спрямована
також як і швидкість.

6. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
III закон Ньютона
Тіла взаємодіють один з одним з силами, рівними за модулем і
протилежними за напрямком:
F12 F21

7. Динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
Закон збереження імпульсу
Механічна система - сукупність тіл, що розглядаються в
задачі. Тіла системи можуть взаємодіяти як між собою, так і з
тілами, що не входять в систему. Сили, що діють на тіла
системи, ділять на внутрішні і зовнішні. Внутрішні сили це сили, з якими тіла системи діють один на одне. Зовнішні
сили - це сили породжені впливом тіл, які не належать
системі. Система, в якій зовнішні сили відсутні, називається
замкнутою.

8. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
Розглянемо систему складається з N частинок (м.т.).
позначимоFik силу, з якою k-а частка діє на i-у. Fi - результуюча
всіх зовнішніх сил, що діють на i-у частку. Користуючись II
законом Ньютона напишемо рівняння руху для N частинок:
dp1
dt F12 F13 ... F1k ... F1N F1
dp
2 F21 F23 ... F2k ... F2N F2
dt
...................................................................
dp
N FN1 FN2 ... FNk ... FN, N-1 FN
dt

9. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
складемо разом ці рівняння. З огляду на III закон Ньютона
отримаємо:
dp N
Fi
dt i = 1
Т.ч., похідна по часу від сумарного імпульсу системи
дорівнює сумі зовнішніх сил, що діють на тіла системи. Якщо
система замкнута, зовнішні сили відсутні і результуюча зовнішніх сил
дорівнює нулю. Звідси робимо висновок, що p = const.
Значить закон збереження імпульсу може бути сформульований
так: «Імпульс замкнутої системи залишається незмінним».
В основі закону збереження імпульсу лежить однорідність простору,
тобто однаковість властивостей простору в усіх точках. Паралельний
перенос замкнутої системи з одного місця в інше без зміни взаємного
розташування і швидкостей частинок не змінює механічних
властивостей системи. Поведінка системи на новому місці буде така ж
сама, як і на колишньому місці.

10. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
Центр мас механічної системи і закон його руху
Точка тіла С, положення якої визначається радіус-вектором
m1 r1 m2 r2 ... m N rN
1 N
rc
mi ri
m1 m2 ... m N
m i=1
називається центром мас системи матеріальних точок. Тут mi маса i-й частки, ri - радіус-вектор, що задає положення цієї частки, mсумарна маса системи. Продиференціювавши rc за часом, знайдемо
швидкість центру мас:
c
p
,
m
де p - сумарний імпульс системи.

11. динаміка матеріальної точки

ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
Значить імпульс системи запишеться p m c .
Використовуючи II закон Ньютона, отримаємо рівняння руху центру мас
системи м.т.:
N
d
m c Fi
dt
i=1
Теорема про рух центру мас механічної системи
Центр мас рухається так, як рухалася б матеріальна точка з масою
рівною масі системи, під дією результуючої всіх зовнішніх сил,
прикладених до тіл (м.т.) системи.

12. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

13. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

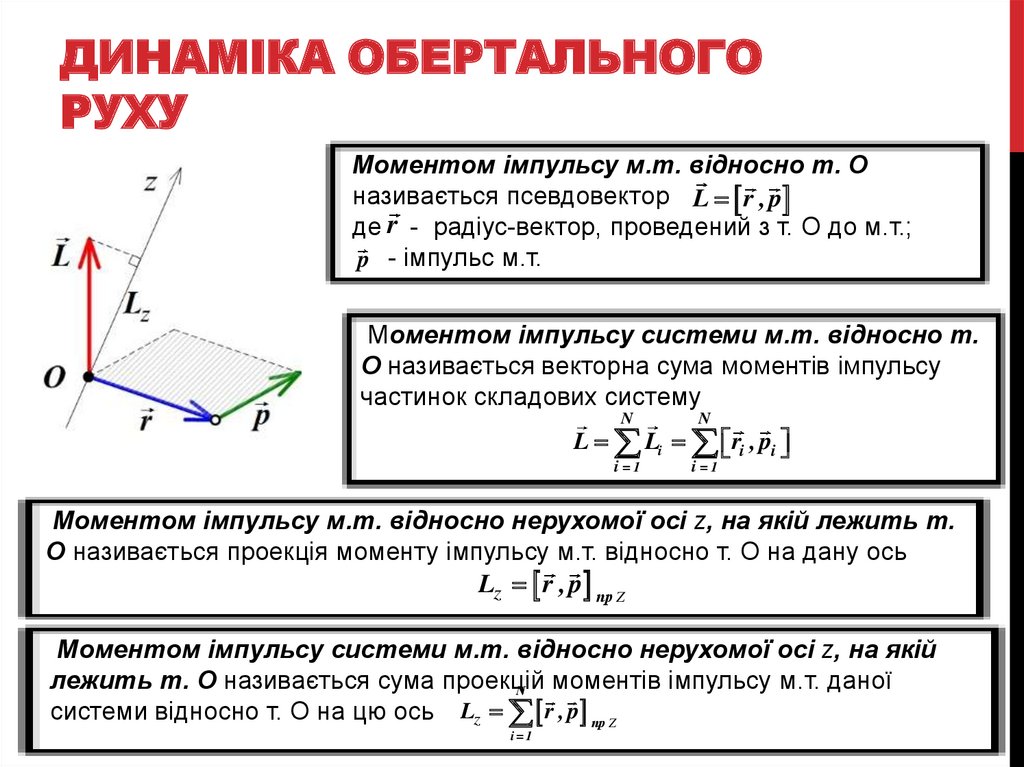
Моментом імпульсу м.т. відносно т. О
називається псевдовектор L r , p
де r - радіус-вектор, проведений з т. О до м.т.;
p - імпульс м.т.
Моментом імпульсу системи м.т. відносно т.
О називається векторна сума моментів імпульсу
частинок складових систему
N
N
i=1
i=1
L Li ri , pi
Моментом імпульсу м.т. відносно нерухомої осі z, на якій лежить т.
О називається проекція моменту імпульсу м.т. відносно т. О на дану ось
Lz r , p пр Z
Моментом імпульсу системи м.т. відносно нерухомої осі z, на якій
лежить т. О називається сума проекцій
моментів імпульсу м.т. даної
N
системи відносно т. О на цю ось Lz r , p пр Z
i=1

14.

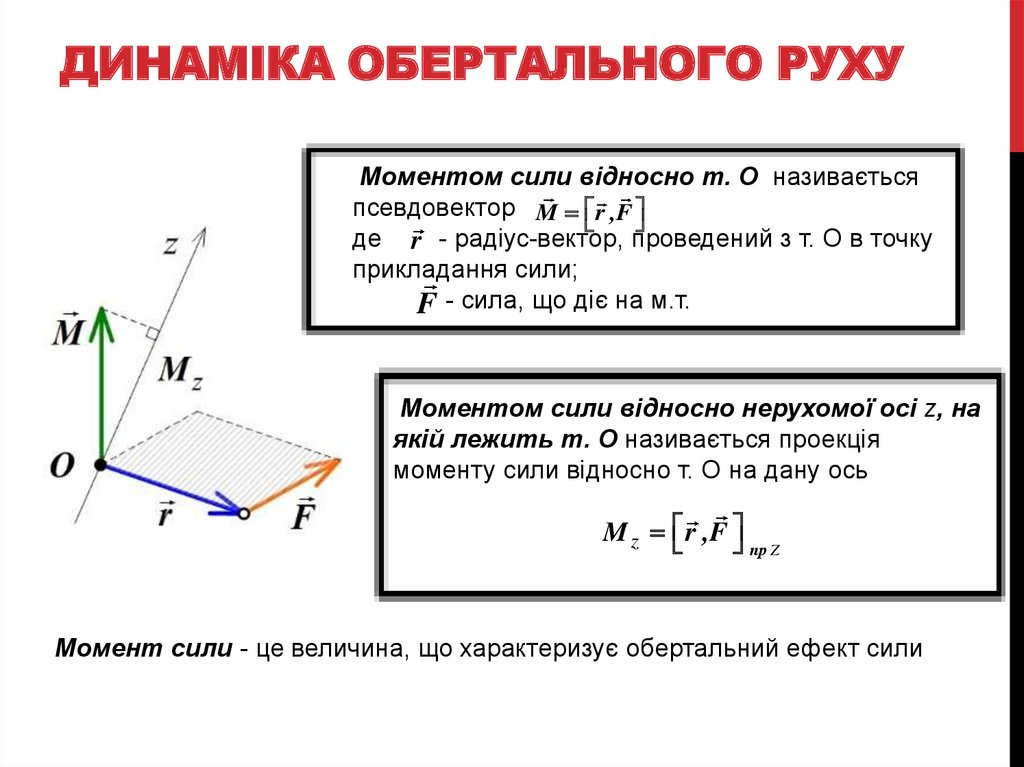
ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ
Моментом сили відносно т. О називається
псевдовектор M r ,F
де r - радіус-вектор, проведений з т. О в точку
прикладання сили;
F - сила, що діє на м.т.
Моментом сили відносно нерухомої осі z, на
якій лежить т. О називається проекція
моменту сили відносно т. О на дану ось
M z r ,F
пр Z
Момент сили - це величина, що характеризує обертальний ефект сили

15. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

МОМЕНТ СИЛИ В ЖИТТІ І ТЕХНІЦІ
Ножиці, пасатижі
Ваги
Армрестлінг
Двері
Застосування різних важелів
в техніці і житті засноване на
понятті моменту сили
Кран
Клавішні
музичні
інструменти

16. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

Момент інерції - це величина, що характеризує розподіл мас в тілі і є
мірою інертності тіла при обертальному русі.
Момент інерції м.т. відносно нерухомої осі обертання z визначається як
Iz m r 2 ,
де m - маса матеріальної точки; r - відстань від осі z до м.т.
Момент інерції системи матеріальних точок відносно осі обертання z - це
величина, що дорівнює сумі моментів інерції матеріальних точок, що
входять в систему, відносно осі z:
Iz
N
m
i= 1
i
ri 2
Вважаючи, що будь-яке тверде тіло є системою матеріальних точок, можна
отримати вираз для розрахунку моменту інерції твердого тіла відносно осі
обертання z:
I z r 2 dm
, де dm - елементарна маса;
r - відстань від dm до z.

17. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

МОМЕНТ ІНЕРЦІЇ В ТЕХНІЦІ
Гончарний круг
(Маховик)
Швейна машинка
(Маховик)
Використовується великий
момент інерції маховиків масивних тіл, що
обертаються - для
накопичення механічної
енергії. Маховик в гіроскопі
зберігає своє початкове
положення, що важливо для
навігації.
Гіроскопи в системах
стабілізації космічних
апаратів
Гіроскопи в МЕМС
мікросхемах Apple iPhone
як датчики положення
Гіроскопи в системах
навігації кораблів і
літаків

18. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

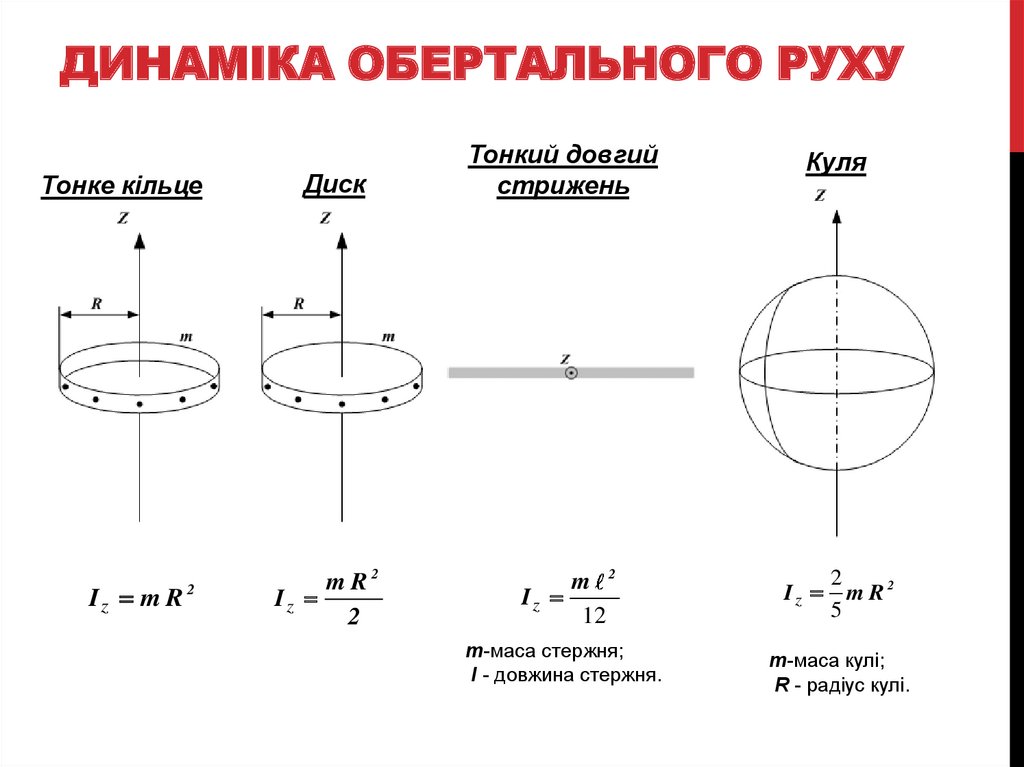
Тонке кільце
Iz m R
2
Диск
m R2
Iz
2
Тонкий довгий
стрижень
m 2
Iz
12
m-маса стержня;
l - довжина стержня.
Куля
Iz
2
m R2
5
m-маса кулі;
R - радіус кулі.

19. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

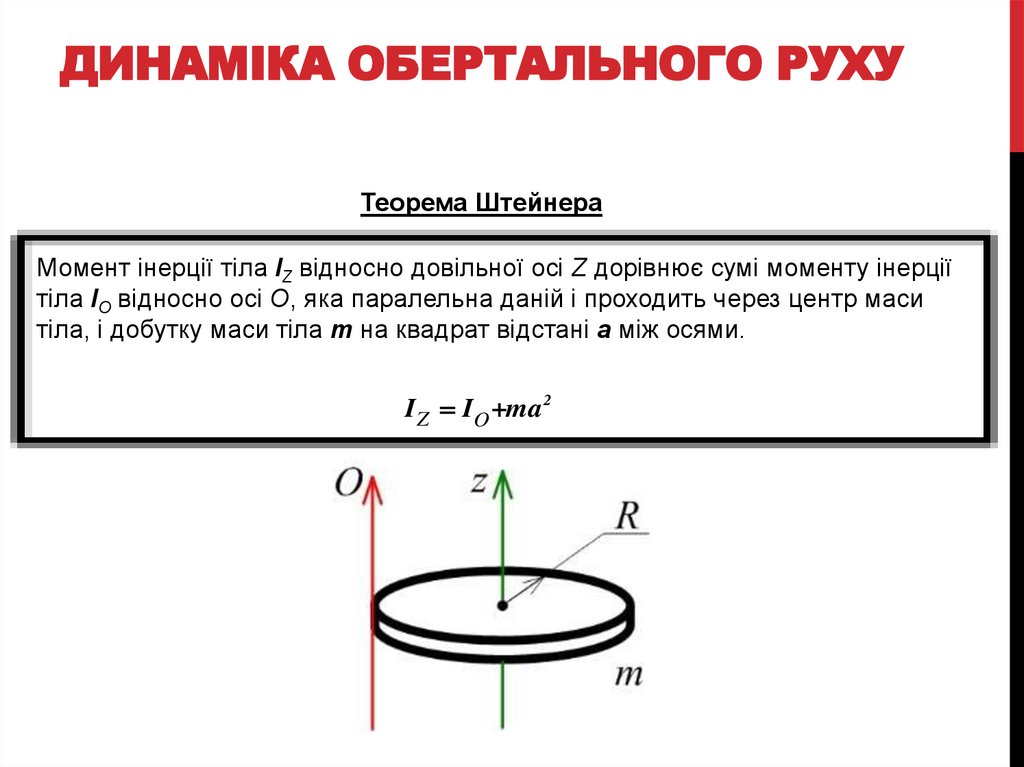
Теорема Штейнера
Момент інерції тіла IZ відносно довільної осі Z дорівнює сумі моменту інерції
тіла IO відносно осі O, яка паралельна даній і проходить через центр маси
тіла, і добутку маси тіла m на квадрат відстані а між осями.
I Z IO +ma 2

20. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

Рівняння моментів
Продиференціювавши за часом вираз моменту імпульсу м.т. відносно точки
отримаємо
dL
M
dt
рівняння моментів для м.т.
Т.ч., за зміну вектора моменту імпульсу м.т. в даній системі відліку
відповідальний результуючий момент всіх сил, прикладених до м.т. Дане
рівняння справедливо при будь-якому русі м.т. по довільній траєкторії.
Рівняння можна узагальнити і для випадку системи м.т. :
dL
M ВН
dt
- рівняння моментів для системи м.т.
Тут M ВН - результуючий момент всіх зовнішніх сил, що діють на систему.
Цей вираз є найбільш загальною формою запису основного рівняння
динаміки обертального руху, оскільки воно справедливо для тіл і
механічних систем як з постійним, так і зі змінним моментом інерції.

21. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

Основне рівняння динаміки обертального руху твердого тіла
відносно нерухомої осі
Між кінематичними і динамічними
обертального руху існує аналогія:
параметрами
поступального
і
F M, p L, m I,
і т.д.
Значит из аналогии p m L I .
Підставивши цей вислів для моменту імпульсу в рівняння моментів для
системи м.т. і врахувавши, що момент інерції незмінний, отримаємо
M I
основне рівняння динаміки обертального руху твердого тіла відносно
нерухомої осі обертання.

22. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

Закон збереження моменту імпульсу
З основного рівняння динаміки обертального руху слідує, що якщо момент
зовнішніх сил дорівнює 0, то момент імпульсу тіла або системи тіл
залишається незмінним:
N
dL
0 L= Li const.
dt
i=1
Момент імпульсу замкнутої механічної системи залишається
незмінним
Закон збереження моменту імпульсу є наслідком ізотропности простору: при
повороті системи відліку на довільний кут не відбудеться зміна результатів
вимірювань в порівнянні з попереднім положенням. Ізотропність простору
означає, що в просторі немає якогось виділеного напрямку, відносно якого існує
«особлива» симетрія, всі напрямки рівноправні.

23. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

24. РОБОТА І кінетична енергія при обертальному русі

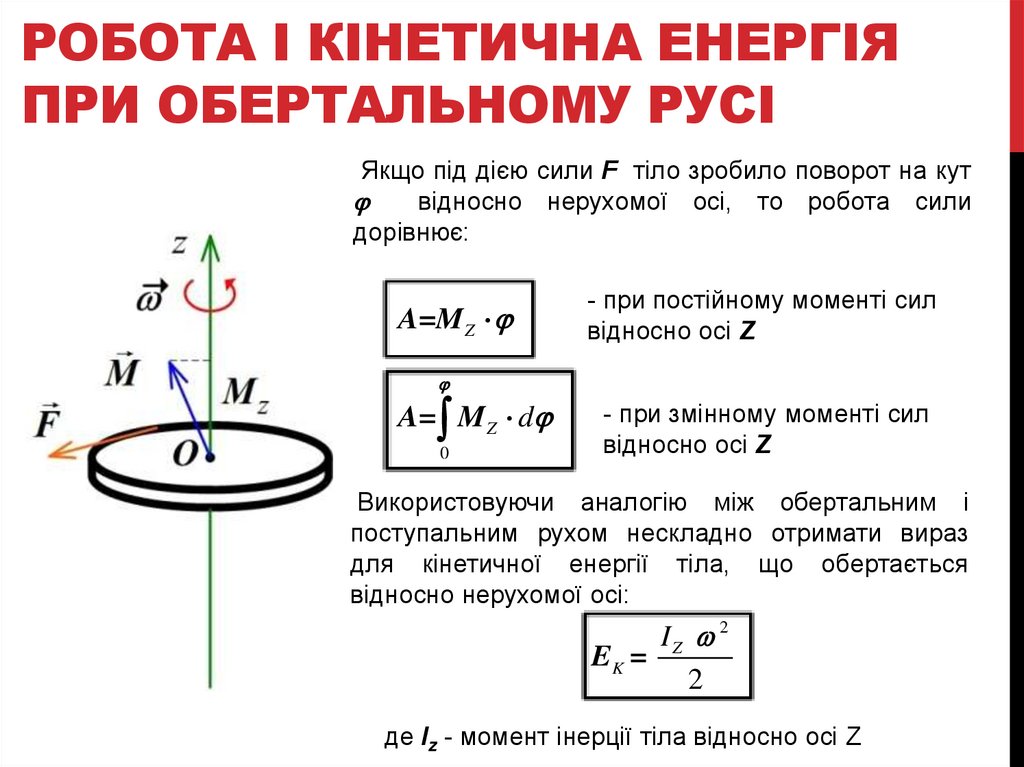
РОБОТА І КІНЕТИЧНА ЕНЕРГІЯ
ПРИ ОБЕРТАЛЬНОМУ РУСІ
Якщо під дією сили F тіло зробило поворот на кут
j
відносно нерухомої осі, то робота сили
дорівнює:
A=M Z j
- при постійному моменті сил
відносно осі Z
j
A= M Z dj
0
- при змінному моменті сил
відносно осі Z
Використовуючи аналогію між обертальним і
поступальним рухом нескладно отримати вираз
для кінетичної енергії тіла, що обертається
відносно нерухомої осі:
IZ 2
EK =
2
де Iz - момент інерції тіла відносно осі Z

25. Кінетична енергія ТІЛА, що котиться

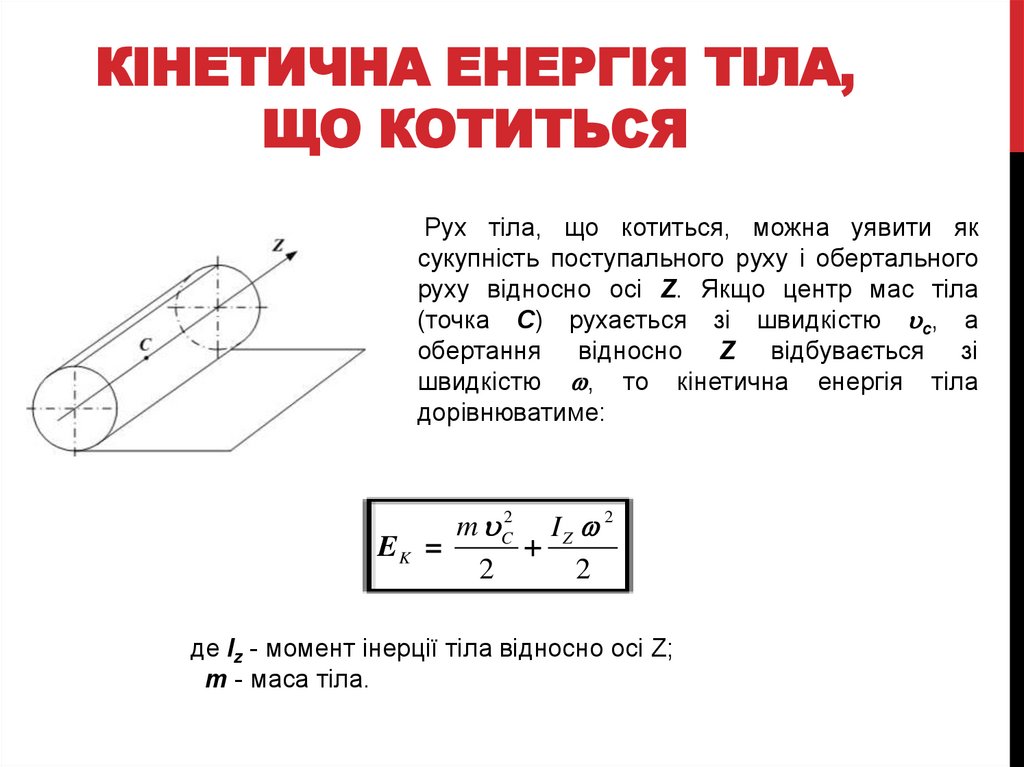
КІНЕТИЧНА ЕНЕРГІЯ ТІЛА,
ЩО КОТИТЬСЯ
Рух тіла, що котиться, можна уявити як
сукупність поступального руху і обертального
руху відносно осі Z. Якщо центр мас тіла
(точка С) рухається зі швидкістю c, а
обертання відносно Z відбувається зі
швидкістю , то кінетична енергія тіла
дорівнюватиме:
m C2 I Z 2
EK =
2
2
де Iz - момент інерції тіла відносно осі Z;
m - маса тіла.