Обертальний рух твердого тіла

1. ОБЕРТАЛЬНИЙ РУХ ТВЕРДОГО ТІЛА

2. ВСТУП

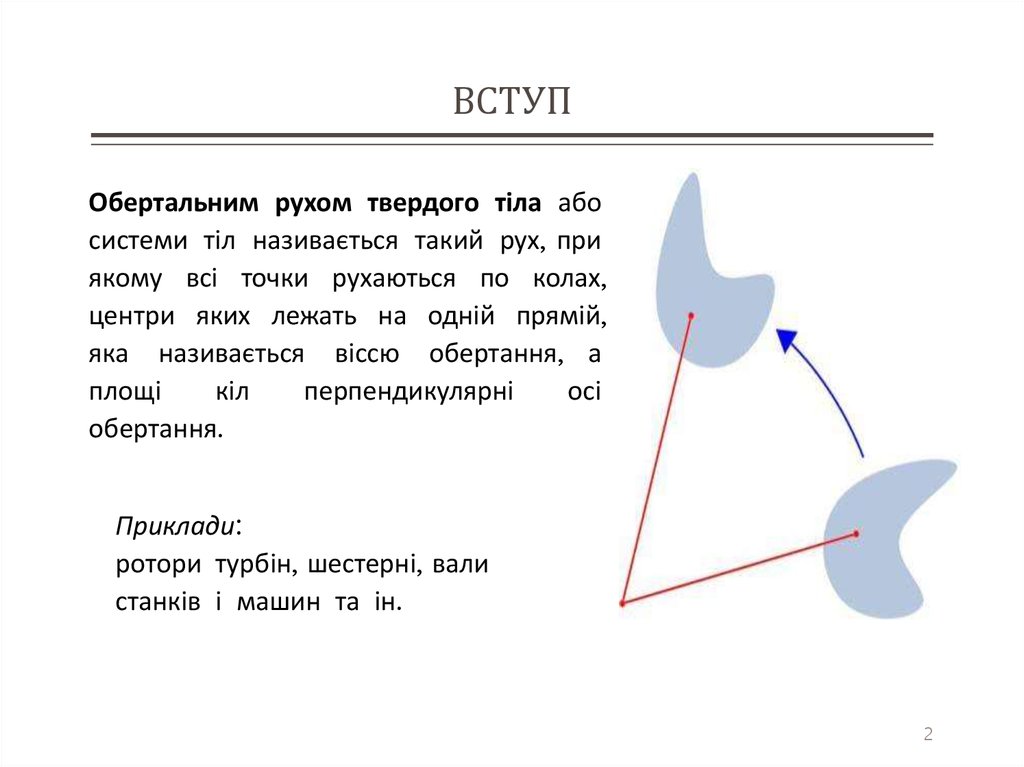
Обертальним рухом твердого тіла або
системи тіл називається такий рух, при
якому всі точки рухаються по колах,
центри яких лежать на одній прямій,
яка називається віссю обертання, а
площі
кіл
перпендикулярні
осі
обертання.
Приклади:
ротори турбін, шестерні, вали
станків і машин та ін.
2

3. ПЛАН

Кінематика обертального руху.
Динаміка обертального руху
Основне рівняння динаміки обертального руху
Динаміка довільного руху
Закони збереження
Закон збереження моменту імпульсу
Кінетична енергія тіла, що обертається
Закон збереження енергії
Висновки
3

4. КІНЕМАТИКА ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА

4

5. НАПРЯМ ВЕКТОРІВ

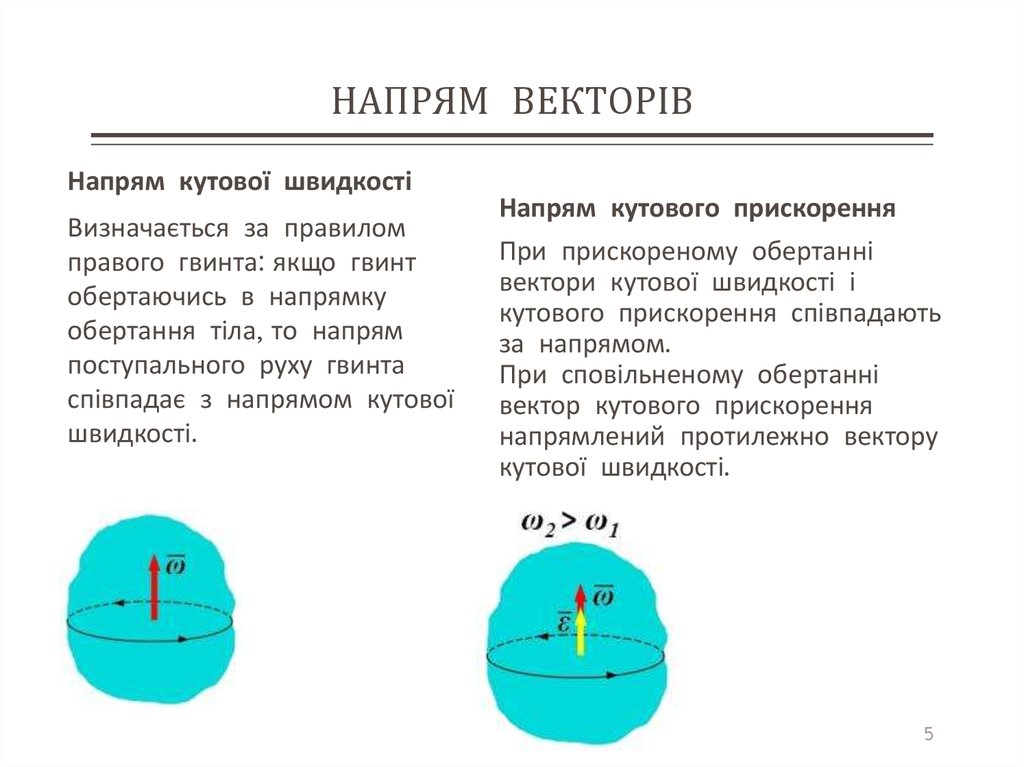
Напрям кутової швидкості
Визначається за правилом
правого гвинта: якщо гвинт
обертаючись в напрямку
обертання тіла, то напрям
поступального руху гвинта
співпадає з напрямом кутової
швидкості.
Напрям кутового прискорення
При прискореному обертанні
вектори кутової швидкості і
кутового прискорення співпадають
за напрямом.
При сповільненому обертанні
вектор кутового прискорення
напрямлений протилежно вектору
кутової швидкості.
5

6. АНАЛОГІЯ РУХУ

Поступальний рух
Переміщення
Обертальний рух
s , s м
Кутове переміщення ,
s
м
,
t
с
рад
рад
,
Швидкість
Кутова швидкість
t
с
рад
м
,
a
,
а
Прискорення
2 Кутове прискорення
t
с2
t
с
Пряма задача кінематики обертального руху
За заданим кутом повороту як функція від часу φ =
f(t) знайти кутову швидкість та прискорення.
Оберенена задача
За заданими кутовим прискоренням як функція від
часу ε = f(t) і початковими умовами ω0 і φ0 знайти
кінематичний закон обертання.
6

7.

Характеристики руху
Рух матеріальної точки по колу
Частота
t
N
N
1
t
T
Кутова швидкість
Період
Кутове прискорення
T
2
2
t
Т
2
2 2 2
t
Т
Переміщення
s r
Лінійна швидкість
Нормальне прискорення
Тангенціальне прискорення
Повне прискорення
S r
r
t
t
2
an
2r
r
r
a
r
t
t
a
a 2 an2
7

8. НАПРЯМ ВЕКТОРІВ ШВИДКОСТІ ТА ПРИСКОРЕННЯ

Нормальне прискорення
Кутова швидкість
По радіусу до центру кола
const
2 1
Перпендикулярно площині рисунка
Лінійна швидкість
const
2 1
По дотичній в напрямку руху
Тангенціальне
прискорення
ні
Кутове прискорення
ні
a
2 1
2 1
a
8

9. ФОРМУЛИ КІНЕМАТИКИ ОБЕРТАЛЬНОГО РУХУ

Поступальний
Обертальний
Рівномірний
а 0
const
0
const
s t
а
0
t
0 а t
t
Рівноприскорений
const
a t
s 0t
2
2
2
0 2а s
2
0
t
0 t
const
t 2
0t
2
2
2
0 2
Нерівномірний
s f (t )
f (t )
s ds
d
s (t )
lim
(t )
t 0 t
t 0 t
dt
dt
d
d
lim
(t )
a lim
(t )
t
0
t
dt
t 0 t
dt
lim
9

10. ДОВІЛЬНІ РУХИ ТВЕРДОГО ТІЛА

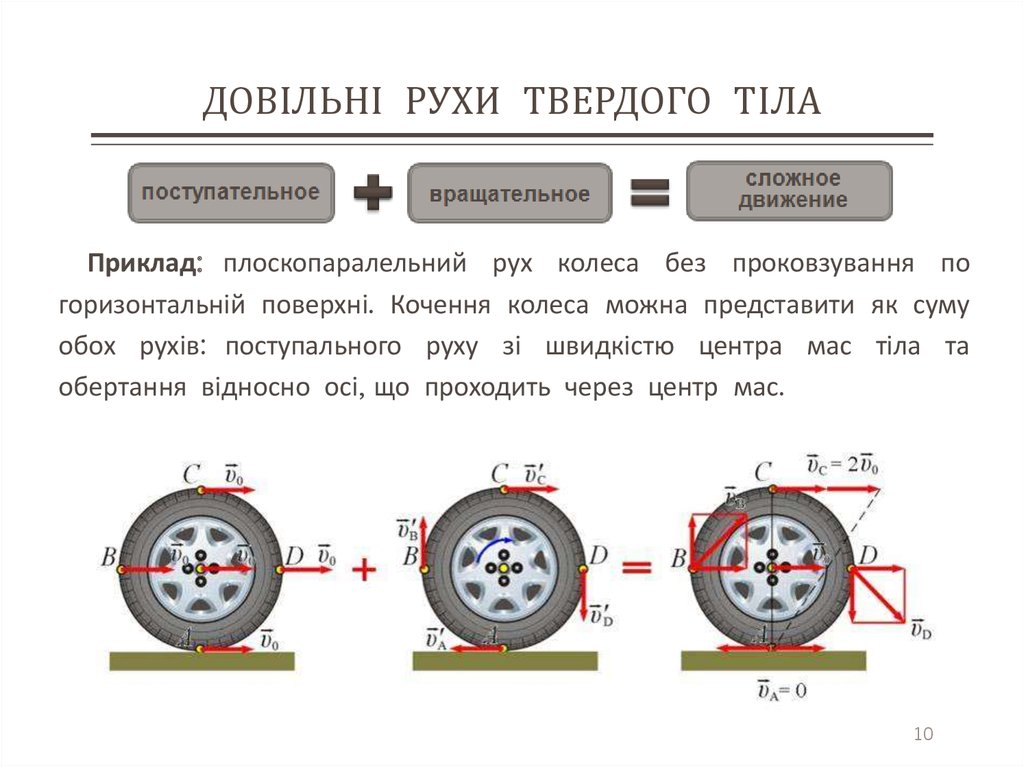
Приклад: плоскопаралельний рух колеса без проковзування по
горизонтальній поверхні. Кочення колеса можна представити як суму
обох рухів: поступального руху зі швидкістю центра мас тіла та
обертання відносно осі, що проходить через центр мас.
10

11. ЯКІСНА ЗАДАЧА

Методом послідовної
зйомки показана
кінематика руху Дворцового
мосту в Санкт-Перербурзі.
Витримка фотографії 6
секунд.
Яку інформацію про рух
моста можна отримати з
фотографії?
Проаналізуйте кінематику
його руху.
11

12. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ ТВЕРДОГО ТІЛА

12

13. Основне рівняння динаміки обертального руху

ОСНОВНЕ РІВНЯННЯ
ДИНАМІКИ
ОБЕРТАЛЬНОГО РУХУ

14. ДИНАМІКА ОБЕРТАЛЬНОГО РУХУ

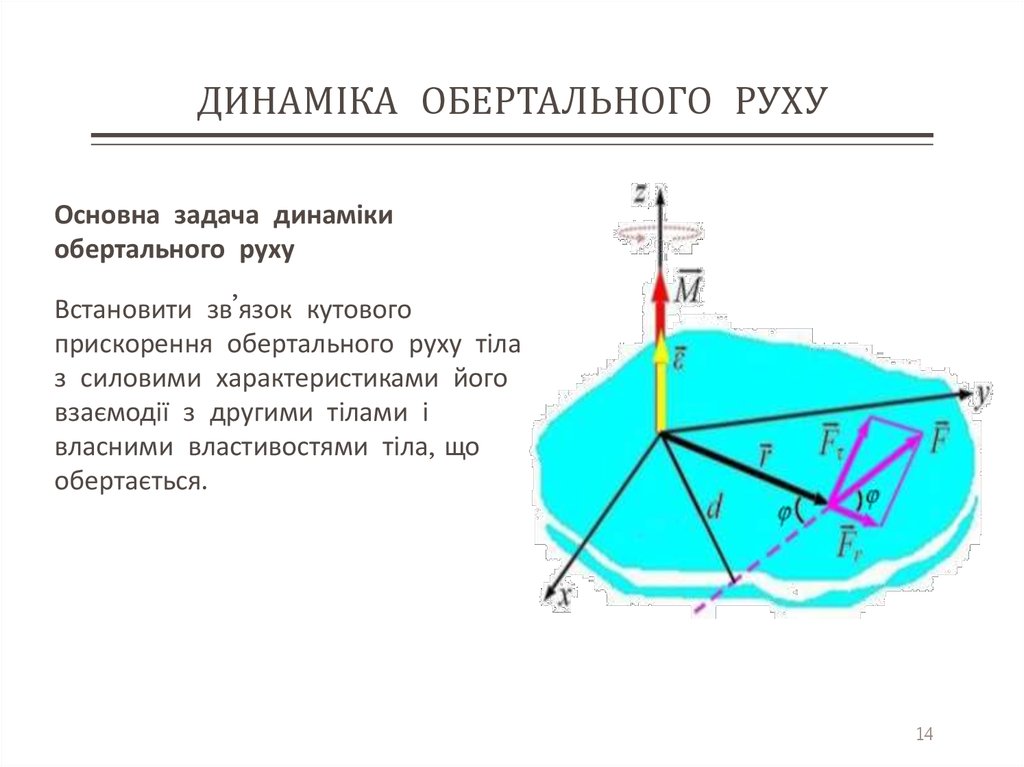
Основна задача динаміки
обертального руху
Встановити зв’язок кутового
прискорення обертального руху тіла
з силовими характеристиками його
взаємодії з другими тілами і
власними властивостями тіла, що
обертається.
14

15. ОСНОВНЕ РІВНЯННЯ ДИНАМІКИ ОБЕРТАЛЬНОГО РУХУ

Для довільної точки тіла
масою m
F Fn F
Для тіла, як сукупності
частинок малих мас
З урахуванням векторного
характера
(m r m r ... m r ) M i M e
2
11
За другим законом Ньютона
Fn man , F ma m r
З геометричних міркувань
F F sin F
d
,
r
mr Fd M
2
2
2 2
2
n n
Скалярная физическая величина,
характеризующая распределение
массы относительно оси вращения,
называется моментом инерции
тела:
I m1r12 m2 r22 ... mn rn2 mi ri 2
Сумма моментов внутренних сил
Мi равна нулю, следовательно
I M e M

16. ПОРІВНЯННЯ РУХІВ

Поступальний рух
Обертальний рух
Маса
Момент інерції
Сила
m, m кг
F , F Н
Момент сили
I kmr2 , I кг м 2
M Fd ; М , M Н м
Основне рівняння динаміки
Основне рівняння динаміки
Прискорення тіла при
поступальному русі прямо
пропорційне сумі всіх діючих на
нього сил і оберенено
пропорційне масі тіла.
Кутове прискорення тіла при
обертальному русі прямо пропорційне
сумі моментів всіх діючих на нього сил
відносно осі обертання тіла і оберенено
пропорційне моменту інерції тіла відносно
цієї осі обертання.
F
a
m
M
I
Принципова різниця: маса є інваріантом, і не залежить від того, як тіло
рухається. Момент інерції змінюється при зміні положення осі обертання або її
напрямлення у просторі.
16

17.

Моменти інерції деяких тіл
Шар
I
2 2
mr
5
Однорідна
пластинка
I
1
m( a 2 b 2 )
12
Тонкостінна
сфера
I
2 2
mr
3
Однорідний
циліндр
I
1 2
mr
2
Однорідний
стержень
I
1
ml 2
12
Товстостінний
циліндр
I
1
m(r12 r22 )
2
Диск
I
1 2
mr
2
Диск
I
1 2
mr
4
Тонкостінный
циліндр
Довільне
тіло
I mr 2
I mi ri 2
17

18. ТЕОРЕМА ШТЕЙНЕРА

Теорема про перенесення осей
інерції (Штейнера): момент інерції
твердого тіла відносно довільної
осі I дорівнює сумі момента
інерції цього тіла I0 відносно осі,
що проходить через центр мас
тіла параллельно осі, яка
розглядається, і добутку маси тіла
m на квадрат відстані d між
осями:
Застосування теореми Штейнера:
Задача. Визначити момент інерції
однорідного стержня довжиною l
відносно осі, що проходить через
один із його кінців
перпендикулярно стержню.
Розв’язок. Центр мас однорідного
стержня розміщений посредині,
тому момент інерції стержня
відносно осі, що проходить через
один із його конців, дорівнює:
2
I I 0 md 2
1 2
l 1 2
I ml m ml .
12
2 3
18

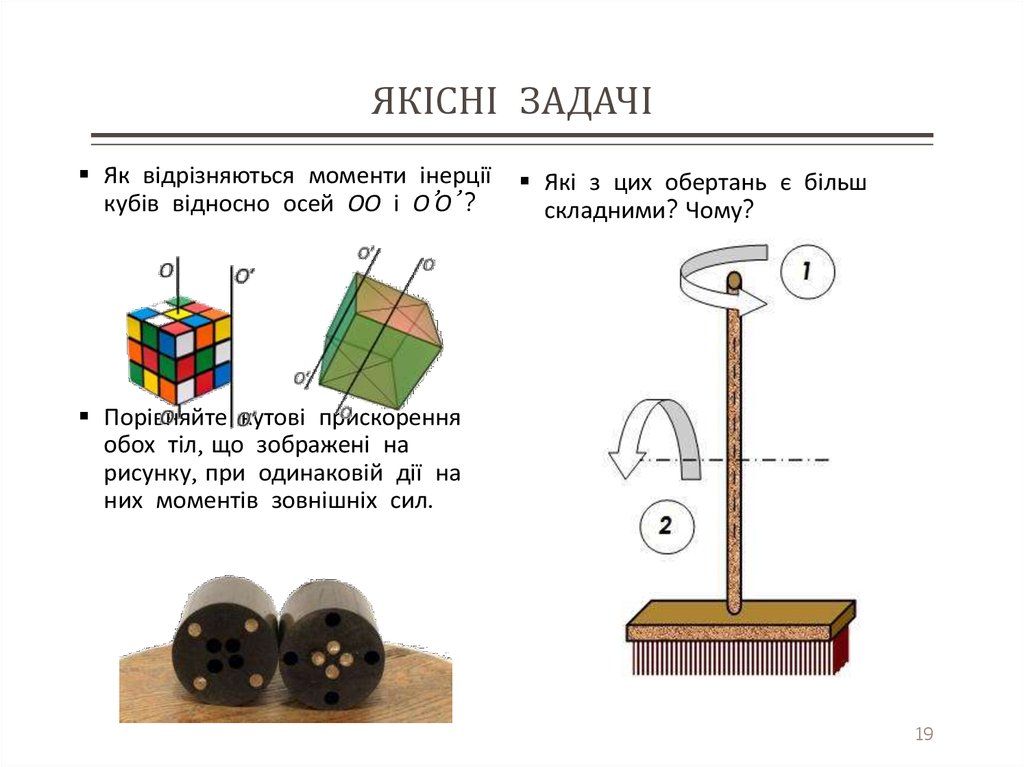
19. ЯКІСНІ ЗАДАЧІ

Як відрізняються моменти інерції
кубів відносно осей ОО і О’О’ ?
Які з цих обертань є більш
складними? Чому?
Порівняйте кутові прискорення
обох тіл, що зображені на
рисунку, при одинаковій дії на
них моментів зовнішніх сил.
19

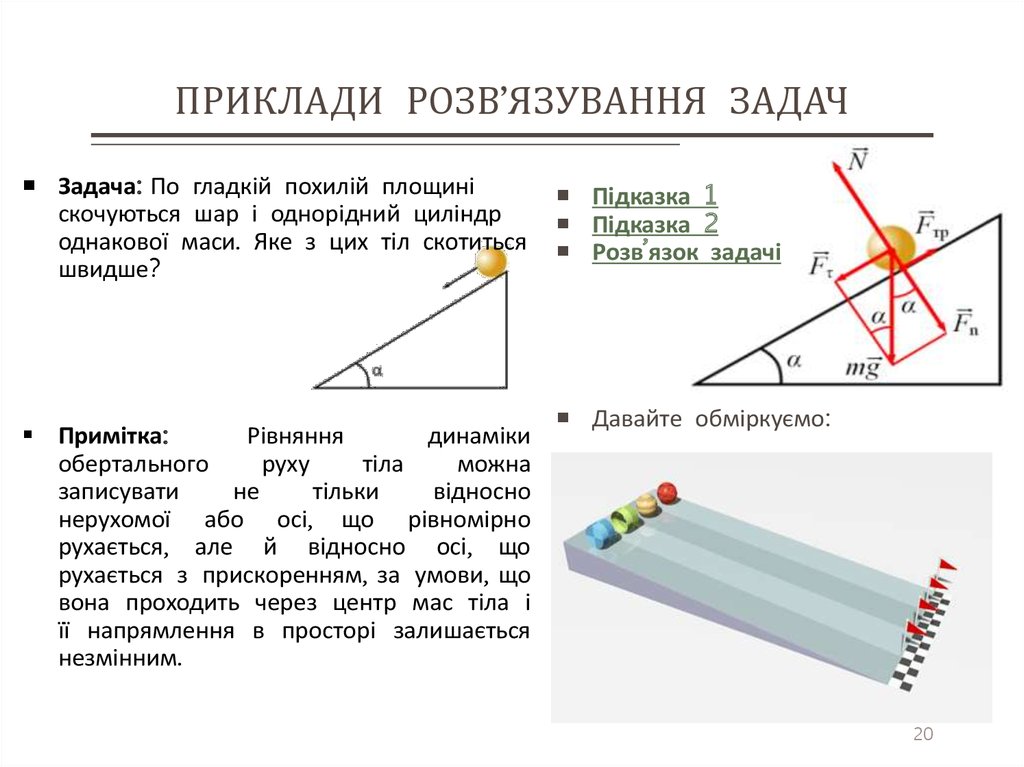
20. ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ

Задача: По гладкій похилій площині
скочуються шар і однорідний циліндр
однакової маси. Яке з цих тіл скотиться
швидше?
Примітка:
Рівняння
динаміки
обертального
руху
тіла
можна
записувати
не
тільки
відносно
нерухомої або осі, що рівномірно
рухається, але й відносно осі, що
рухається з прискоренням, за умови, що
вона проходить через центр мас тіла і
її напрямлення в просторі залишається
незмінним.
Підказка 1
Підказка 2
Розв’язок задачі
Давайте обміркуємо:
20

21. Підказка 2

ДИНАМІКА
ДОВІЛЬНОГО РУХУ

22. Розв’язок задачі

ДИНАМІКА ДОВІЛЬНОГО РУХУ
Довільний рух твердого тіла можна розкласти на поступальний рух, в якому
всі точки тіла рухаються зі швидкість центра мас тіла, та обертання центра
мас.
Теорема про рух центра мас: центр мас
механічної системи рехається як матеріальна
точка масою, яка рівна масі всієї системи, до
якої прикладені всі зовнішні сили, що діють
на систему.
Наслідки:
Якщо вектор зовнішніх сил системи рівний нулю, то
центр мас системи або рухається з постійною за
величиною
ті
напрямком
швидкістю,
або
знаходиться в стані спокою.
Якщо сума проекцій зовнішніх сил на будь-яку вісь
дорівнює нулю, то проекція вектора швидкості руху
центра мас системи на цю вісь або const, або
рівна нулю.
Внутрішні сили не впливають на рух центра мас.
24

23. ДИНАМІКА ДОВІЛЬНОГО РУХУ

ІЛЮСТРАЦІЯ ТЕОРЕМИ
Режим послідовної
зйомки дозволяє
проілюструвати теорему
про рух центра мас
системи:
при спуску затвора за
одну секунду можна
відобразити кілька
зображень.
При об'єднанні такої серії
спортсмени, які виконують
трюки, і тварини в русі
перетворюються в щільну
чергу близнюків.
25