Лекція 6. Визначення напружень при згинанні. Умови міцності при згинанні

1.

Лекція 6
ВИЗНАЧЕННЯ НАПРУЖЕНЬ ПРИ ЗГИНАННІ. УМОВИ МІЦНОСТІ ПРИ ЗГИНАННІ
1
Плоский згин.
При поперечному плоскому згині із шести внутрішніх силових факторів відмінними від нуля є два:
поперечна сила і згинаючий момент, при чому вони повинні виникати в одній площині.
Q y 0
M y 0
N Qz M y
Q y 0 Вплощині Вплощині
Qz 0
XOY діють XOY діють
M y 0
M y 0
всі
силові
всі силові
M
Nкр
Qz0 M y M кр 0 N Qz M z
фактори
фактори
Qz 0 Вплощині
XOZ діють
M y 0
всі силові
M
Nкр Q0z M z M кр 0
фактори
Вплощині
XOZ діють
всі силові
фактори
Плоским називається згин, при якому всі силові фактори, що діють на тіло, обов'язково прикладені в
одній і тій же площині і ця площина обов'язково співпадає з одною із головних площин інерції перерізу.
Так як при плоскому згині в загальному випадку одночасно два силових фактори відмінні від нуля, то в
будь-якій довільній точці довільного перерізу по довжині стержня виникають два напруження :
– нормальне напруження σ, величина і знак якого залежить від згинаючого моменту М;
– дотичне напруження τ, величина і знак якого залежить тільки від поперечної сили Q.
Для визначення нормальних напружень розглянемо окремий випадок плоского згину – чистий згин.
В цьому випадку навантаження, із шести внутрішніх зусиль залишається тільки згинаючий момент M в
одній площині.

2.

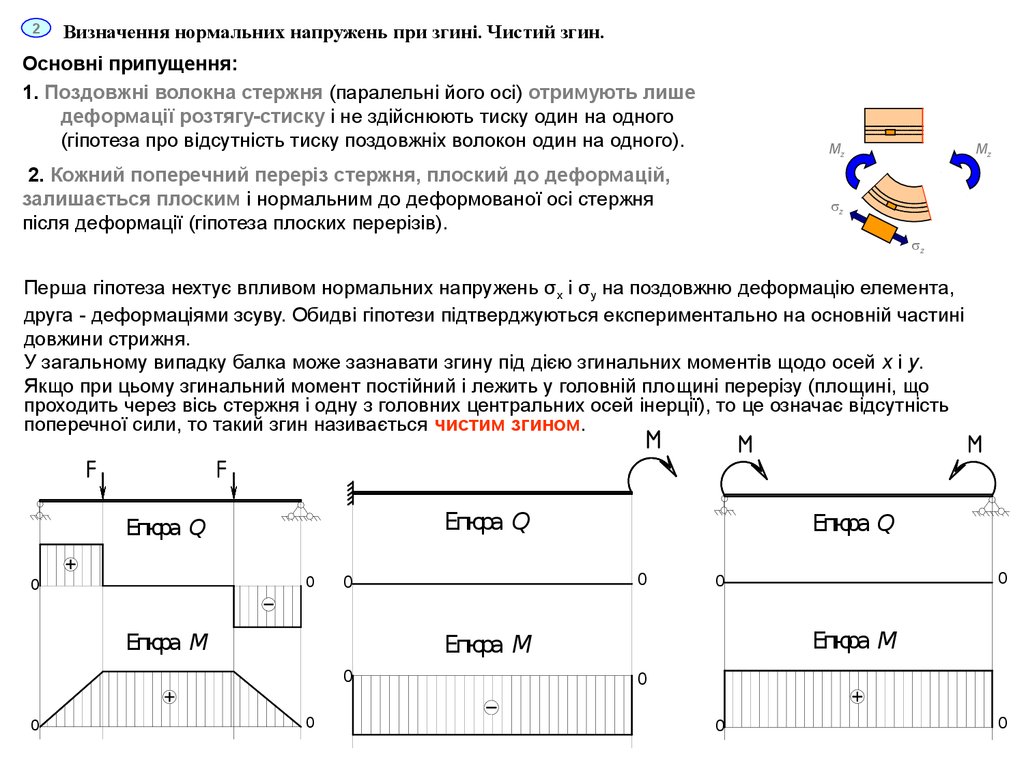
2
Визначення нормальних напружень при згині. Чистий згин.
Основні припущення:
1. Поздовжні волокна стержня (паралельні його осі) отримують лише
деформації розтягу-стиску і не здійснюють тиску один на одного
(гіпотеза про відсутність тиску поздовжніх волокон один на одного).
Mz
2. Кожний поперечний переріз стержня, плоский до деформацій,
залишається плоским і нормальним до деформованої осі стержня
після деформації (гіпотеза плоских перерізів).
Mz
z
z
Перша гіпотеза нехтує впливом нормальних напружень σ x і σy на поздовжню деформацію елемента,
друга - деформаціями зсуву. Обидві гіпотези підтверджуються експериментально на основній частині
довжини стрижня.
У загальному випадку балка може зазнавати згину під дією згинальних моментів щодо осей x і y.
Якщо при цьому згинальний момент постійний і лежить у головній площині перерізу (площині, що
проходить через вісь стержня і одну з головних центральних осей інерції), то це означає відсутність
поперечної сили, то такий згин називається чистим згином.
Епюра Q
Епюра Q
0
0
0
0
0
Епюра М
Епюра М
0
0
0
0
Епюра М
Епюра Q
0
0
0

3.

Підставимо напруження
æ
yзадача
E 2напружень є
0 ö
Нормальні напруження упри
чистому
згині. Як зазначалося
визначення
M z - раніше,
E
ydA
y dA.
вираз
для згинального
ç розглянути
÷
статично невизначеною, длямоменту
вирішення
якої
необхідно
послідовно
три
сторони
задачі:= I
(y y ) :
òè
A
0
z
z
dz
y
Mz
z
Δdz
2
y
z
y0
y0
dz
zdA
–
z
z0
+
Δdz
2
ò
A
x
1. Статика: Виділимо малий елемент двома нормальними до осі
бруса перерізами і замінимо дію відкинутих частин нормальними
M
1 M z Під їх дією елемент знаходиться
напруженнями.
- z y. в рівновазі.
.
Mz
A
ø
I x і центральних осей
EI x розподілених сил до центру
Вище приведенням
було отримано інтегральні співвідношення, що зв'язують нормальні
Формула Навьє.
Рівняння
зігнутої
осі балки.
зусилля
і згинальний
момент з нормальними напруженнями:
M z - ò z ydA.
dA
y
x
A
N ò z dA;
A
Зауваження: Знак мінус враховує правило
знаків для згинального моменту і напружень.
Так як нормальні зусилля
при згині дорівнює нулю, то:
ò dA 0.
z
A
Останнє судження вказує на те, що в перерізі виникають напруження різного знаку і слід
припускати, що існують волокна, в яких напруження дорівнюють нулю (нейтральна вісь).
З цих співвідношень знайти напруження і положення нейтральної осі поки не можна,
оскільки закон зміни напружень по висоті перерізу невідомий.
2. Геометрія: Відповідно до гіпотези плоских перерізів, поздовжні волокна отримують деформації
розтягу-стиску, пропорційні відстані від нейтральної осі. Нейтральна вісь, як і центральна вісь
стрижня, вигинається і має радіус кривизни (т. А – центр кривизни).
y0
Абсолютне видовження волокна, що знаходиться
dz y0
Ddz
D
dz
2
dz.
ez
на довільній відстані від нейтральної
2
dz
осі, з подібності трикутників дорівнює:
-
y0
.
y0 Таким чином, нормальні напруження лінійно залежать
y
E
. Закон Гука при згині.
z E e z .
0
z
від відстані до нейтральної осі.
dzE/ 2 Ddz / 2
y0
Підставимо зусилля
E
dA
y0 dA 0.Цей інтеграл являє собою статичний момент площі і рівність
у вираз для
ò
ò
A
нормальної сили:
його нулю означає, що нейтральна вісь проходить через центр ваги.
A
3. Фізика: По закону Гука:

4.

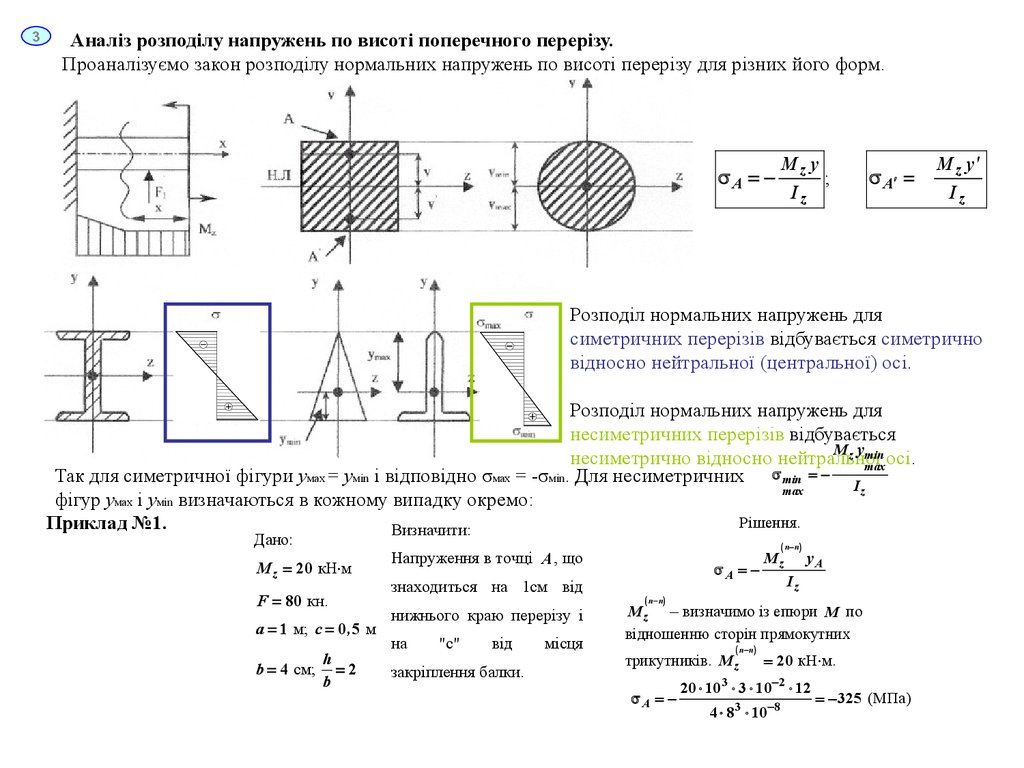
3
Аналіз розподілу напружень по висоті поперечного перерізу.
Проаналізуємо закон розподілу нормальних напружень по висоті перерізу для різних його форм.
A -
Mz y
;
Iz
A -
M z y'
Iz
Розподіл нормальних напружень для
симетричних перерізів відбувається симетрично
відносно нейтральної (центральної) осі.
Розподіл нормальних напружень для
несиметричних перерізів відбувається
M z ymin
несиметрично відносно нейтральної
осі.
max
Так для симетричної фігури умах = умin і відповідно σмах = -σмin. Для несиметричних min - I
max
z
фігур умах і умin визначаються в кожному випадку окремо:
Рішення.
Приклад №1.
Визначити:
Дано:
M z 20 кН м
F 80 кн.
a 1 м; c 0 , 5 м
h
b 4 см; 2
b
n- n
Напруження в точці A , що
знаходиться на 1см від
нижнього краю перерізу і
на
"с"
від
закріплення балки.
місця
A -
Mz
yA
Iz
n- n
M z – визначимо із епюри M по
відношенню сторін прямокутних
n-n
трикутників. M z
A -
20 кН м.
20 10 3 10-2 12
3
4 83 10-8
-325 (МПа)

5.

Поняття раціонального перерізу при згині. З формули напружень при згині випливає, що найбільші (позитивні розтягучі) і найменші (негативні - стискаючі) напруження в поперечному перерізі залежать від величини осьового
Mz
Mz
моменту інерції або осьового моменту опору:
max
Ix
ymax .
max
Wx
.
При зміні розмірів перерізу змінюються як осьовий момент опору, так і площа перерізу. При цьому величина осьового
моменту опору залежить, наприклад, для прямокутного перерізу, від квадрата висоти перерізу, а площа - лінійно.
Збільшенням площі збільшує витрату матеріалу на виготовлення балки. Більш раціональним перерізом вважається
такий, при якому відношення моменту опору до площі має більше значення. Для цього слід якомога більшу частину
площі поперечного перерізу розташовувати якомога далі від нейтральної осі.
Нижче показано 5 поперечних перерізів балки, складених з нерівнополичкових кутиків і листів, площа всіх перерізів
однакова, а моменти опору різні:
У зв'язку з тим, що площі цих перерізів однакові, найбільш
раціональним з них є той, у якого момент опору Wx більший.
■ Домогтися зниження ваги балки можна також шляхом зміни
розмірів перерізу по її довжині відповідно до зміни величини
згинального моменту.
Оскільки епюра згинального моменту має в загальному випадку
криволінійний обрис, то для отримання раціонального перерізу
розміри, наприклад висота або товщина полиць, повинні
безперервно змінюватися.
З технологічних міркувань замість цього використовують ступеневу
зміну товщини, що досягається приварюванням або
приклепуванням додаткових горизонтальних листів:
На малюнку зображена, так звана, епюра матеріалів, ординати
якої дорівнюють добутку моменту опору поперечного перерізу на
допустимі напруження :
M z Wx [ ] .

6.

4
Умови міцності по нормальних напруженнях при плоскому згині.
Максимальні напруження не повинні перевищувати
розрахункових або допустимих напружень.
max
Mx
[ ].
Wx
У всіх випадках, крім круглого перерізу, потрібно використовувати моменти опору, відповідні орієнтації площини дії згинального моменту.
Наприклад, при дії на балку прямокутного перерізу моменту Mx
при обчисленні максимальних нормальних напружень необхідно використовувати Wx:
А при дії на балку прямокутного перерізу моменту My
при обчисленні максимальних нормальних напружень необхідно використовувати Wy:
Три види задач при згині:
M
max max [ ] .
1. Умова міцності
Wx
2. Визначення допустимих навантажень
3. Підбір перерізу
Приклад №2.
M
Wx max
[ ]
max
Mx
[ ].
Wx
max
My
[ ].
Wy
M доп [ ]Wx
Для попередніх умов навантаження провести перевірку міцності, якщо
переріз являє собою двутавр №14 ( Wx 81.7 cм3) із Cт 3 ( [ ] 160 МПа).
max
max
M max
[ ].
Wx
60 103
722 МПа < [ ] 160 МПа
81.7 10 -6
Таким чином двотавр №14 не задовольняє умові міцності
для заданої розрахункової схеми.

7.

5
Підбір перерізу при згині.
Для того, щоб визначити необхідні розміри поперечного перерізу потрібно:
1. Побудувати епюру згинаючих моментів;
2. На цій епюрі визначити переріз, де діє максимальний по модулю згинаючий момент Mmax;
3. По вихідній нерівності Wнеобх > Mmax/[σ], потрібно розрахувати величину необхідного моменту опору Wнеобх, попередньо
визначивши допустиме напруження для даного матеріалу [σ];
4. Знаючи величину необхідного моменту опору Wнеобх і форму поперечного перерізу потрібно розрахувати відповідні
розміри перерізу чи підібрати номер прокатного сталевого профілю.
При цьому, враховуючи епюру розподілу нормальних напружень по висоті перерізу, в умовах дії плоского згину, завжди
потрібно пам’ятати про те, що найраціональнішою формою перерізу є двотавр.
У випадку, наприклад, прямокутного перерізу
необхідно задати один з розмірів або співвідношення
між ними. Нехай h / b = k.
Тоді необхідна висота перерізу:
h необх 3 6kW необх
x
Приклад №3.
Для попередніх умов завантаження підібрати двотавровий поперечний переріз, якщо
балка виготовлена із сталі Ст3 [σ]=160МПа.
Wx.необх
M x 60 103
0.375 10 -3 375 10 -6 м3 = 375 см3
6
[ ] 160 10
По сортаменту прокатних профілів приймаємо двотавр №27 (W x = 371 cм3).
Перевірка підібраного перерізу на міцність:
60 103
161.7 МПа
371 10 - 6
161.7 - 160
D
100% 1.05% 5%
Перенапруження:
161.7
Отже, умова міцності підібраного поперечного перерізу (двотавра №27) забезпечена.

8.

6
Дотичні напруження при згині.
Прямий поперечний згин - в поперечному перерізі балки, крім згинального моменту, діє також поперечна сила.
При прямому поперечному згині згинальний момент діє в площині, що збігається з однією з головних площин інерції поперечного перерізу
балки. Поперечна сила при цьому зазвичай паралельна площині дії згинального моменту.
■ Дотичні напруження при поперечному згині - У загальному випадку при поперечному згині балок довільного профілю можуть
виникати дві компоненти повного дотичного напруження в перерізі. Компонента zx для такого перерізу не може бути знайдена методами
опору матеріалів. Дотичні напруження zy, що виникають в поперечному перерізі, пов'язані з поперечною силою, що діє
в цьому перерізі бруса, інтегральною залежністю:
F
Mz
Qy ò zy dA.
Qy
A
Mz+dMz
z
Виділимо малий елемент двома нормалями до осі бруса і замінимо дію відкинутих частин
нормальними напруженнями та дотичними напруженнями. Під їх дією елемент знаходиться в
рівновазі.
Qy
z
dz
zy z z+d z
z zy
yz
A1
Aвідс
zx
b
При дії поперечної сили згинальний момент у перерізі, віддаленому на відстані dz від іншого
перерізу, має приріст dMz.
y
zy
згідно залежності
dA
y
z
dz
Оскільки закон зміни дотичних напружень по перерізу невідомий,
то з цього рівняння знайти дотичні напруження для відомої поперечної сили
не можна.
x
Mz
y
Ix
нормальні напруження також отримують збільшення :
d
dM z
y.
Ix
Відсічемо від розглянутого елемента деяку її частину горизонтальною площиною і замінимо
її дію дотичними напруженнями (нормальні напруження відповідно до гіпотезою про
відсутність здавлювання поздовжніх волокон не розглядаються).
Залишений елемент як і раніше знаходиться в рівновазі. Рівняння рівноваги в проекції на вісь z:
Zi 0;
- ò ( z d z )dA
Aвідс
ò z dA ò yz dA 0.или
Aвідс
A1
- ò d z dA ò yz dA 0.
Aвідс
A1
Тут Aвідс – площа відсіченої частини поперечного перерізу,A1 – площа горизонтального перерізу елемента, що дорівнює bdz.
ò
ò
dM
z
Перенесемо перший інтеграл в праву частину і підставимо в нього вираз для нормальних напружень: yz dA
ydA.
I
Приріст згинального моменту і осьовий момент інерції перерізу не залежать від площі
x
A1відс
A
відсіченої частини і їх можна винести за знак інтеграла. Залишений підінтегральної вираз співпадає з
dM z
dM z
yz dA
ydA
виразом для статичного моменту площі відсіченої частини поперечного перерізу:
Ix A
Ix
Вважаючи дотичні напруження постійними за площею A1, що відповідає припущенням сталості
A1відс
деформацій зсуву по ширині поперечного перерізу, враховуючи закон парності дотичних
переміщень і диференціальну залежність
Qy S xвідс
dM z S xвідс
- формула
dM z відс
. Журавського
zy
або zy
поперечної сили, отримуємо:
bdz
S .
ò
zy
Ix
x
dz
I xb
ò
I xb
S xвідс .

9.

Розподіл
дотичних напружень по висоті перерізу - З формули Журавського випливає,
що дотичні напруження у волокнах поперечного перерізі, розташованих на деякій відстані від осі,
залежать від величини статичного моменту площі відсіченої частини і ширини перерізу на висоті січної площини:
Побудуємо епюри дотичних напружень для деяких простих перерізів:
прямокутний переріз
Проведемо горизонтальний переріз на висоті y
h
æ
ö
і обчислимо статичний момент
y
ç
÷ æh
відсіченої частини:
ö 1
відс
2
Sx
y
Aвідс
yo
y
yo Aвідс ç y
çç
è
Підставимо у формулу Журавського
вирази для статичного моменту
і моменту інерції:
x
h
Qy
zy
ö
1 æ h2
÷bç - y ÷ (2 y h)b(h - 2 y ) çç - y 2 ÷÷b.
2 ÷ è2
2è 4
ø 8
ø
÷
ø
1 æ h2
2ö
ç
÷b
y
÷
2 çè 4
ø
bh
3
6Q y æ h 2
3Q y æ 4 y 2
2ö
ç
÷
ç
y
÷ 2bh ç1 - h 2
bh 3 çè 4
ø
è
Отримана залежність є
b
12
квадратичною від координати розглянутого шару.
Таким чином, дотичні напруження по висоті
перерізу змінюються за квадратною параболою: y = h/2, zy = 0; y = 0, zy = zymax =3Qy/(2bh) =1,5 zyср
b
Можна переконатися, що об’єм епюри напружень τzy (y) · b / Qy дорівнює 1, що означає виконання рівності.
y
S xвідс
H h
H -hö
æ
çH
÷ æ H - h ö 1 æ h2
2ö
2
÷ Bç
ç ÷ çç - y1 ÷÷b
2 ÷ è 2 ø 2è 4
çç 2
ø
÷
è
ø æ 2
ö
Для стінки:
y1
y2
x
Для полички:
b
B
Qy ò zy dA.
Переріз має ступеневу зміну ширини і тому слід розглядати окремо дві ділянки
зміни координати: 0 <y1<h / 2 - стінка і h / 2 <y2<H / 2 - полку.
■ Товстостінний двотавр
S
1
1 h
( H 2 - h 2 ) B çç
- y12 ÷÷b.
4
2è 4
ø
відс
x
ö
1æ H2
çç
- y22 ÷÷ B.
2è 4
ø
На обох ділянках дотримується квадратична залежність від
координати волокна. У місцях різкої зміни ширини перерізу
відповідно до формули Журавського епюра має скачки:
Qy S xвідс
zy
.
I xb
A
ö
÷.
÷
ø

10.

7
Головні напруження при згині.
Аналіз
напруженого стану при згині - Вище були отримані і розглянуті вирази для нормальних
і дотичних напружень, що виникають при згині. При розрахунках на міцність повинні бути визначені ті перерізи і ті
волокна, в яких ці напруження досягають максимальних значень. І це різні перерізи і різні волокна. Наприклад, при поперечному
згині двохопорної балки максимальний згинальний момент виникає в середині прольоту, а максимальна
поперечна сила - в опорних перерізах.
zy
При цьому максимальні нормальні напруження виникають у найбільш
віддалених волокнах, а максимальні дотичні напруження на нейтральній осі.
y
z
Qy
Q y S xотс
I xb
При поперечному плоскому згині
x = z = , y = 0, yx = yz = :
Тоді отримуємо:
1, 2
y
1, 2
x y 1
( x - y ) 2 4 yx2 .
2
2
2
1
2 4 2 . tg 2 .
2 2
tg 2
2 yx
x - y
Визначивши величини головних напружень
для ряду точок даного перерізу
на різній відстані від нейтральної осі,
можна побудувати епюри головних напружень:
.
В елементі балки, що знаходиться в деякому перерізі, в якому одночасно діють досить великі
згинальний момент і поперечна сила, на довільній відстані від нейтральної осі, виникають
одночасно нормальні і дотичні напруження.
Головні напруження в цьому елементі і тангенс
кута нахилу головних площадок визначаються
виразами:
Mx
Mz
y.
Ix
2
x
1
Оскільки епюри дотичних напружень мають скачки
в місцях різкої зміни ширини поперечного перерізу
(двотавр, швелер), то це знайде своє
відображення на епюрі головних напружень.
Наочне уявлення про потік внутрішніх сил в тілі (стінці) балки можуть дати траєкторії головних напружень - ліній, в кожній точці яких дотична
співпадає з напрямом головного напруження в цій точці. На малюнку показані траєкторії розтягуючих головних напружень. Вони перетинають
нейтральну вісь під кутом 450.
При армуванні бетону сталевими стрижнями враховується характер
цих траєкторій, т.я. бетон погано чинить опір розтягуванню:
Траєкторії стискаючих головних напружень враховуються при постановці
ребер жорсткості для запобігання випучування тонких стінок, внаслідок
наявності стиснутих областей у стінці.
Аналіз напруженого стану при згині балки показує, що необхідно перевіряти умови міцності за нормальними напруженнями в крайніх
волокнах перерізів з максимальною величиною згинального моменту (у середині прольоту), по дотичним напруженням - на нейтральній
осі опорних перерізів і за головними напруженням - в точках з'єднання стінки і полки перерізів, в яких діють згинальний момент і
поперечна сила.
.

11.

Епюри розподілу дотичних напружень по висоті перерізу для різних його форм
Використовуючи формулу Журавського
Q Sz
b Iz
будемо вважати, що
2. Для круглого перерізу:
поперечна сила Q задана і, що вона. додатна.
max K ср , де K 1.33 .
1. Тоді для прямокутного перерізу:
max K ср , де K 1.5 .
max 0 , т.як Q 0
max
max
Q S z max
4
d
D
64
QD 3 64
12 D D 4
Розглянемо довільний шар на відстані " y " і розрахуємо дотичні напруження в
Q Sz
b Iz
æh
Sz ç è2
Оскільки сер
bh2 æ
4 y2 ö
çç 1 - 2 ÷÷
8 è
h ø
bh3
b
12
ö
y÷ b y
ø
1æ h
2 çè 2
2 Q æ
4 y2 ö
çç 1 - 2 ÷÷ , де
3 bh è
h ø
cep
4 Q
1.33 cep –
3 D 2
4
2
4 y2 ö
ö bh æ
y ÷
çç 1 - 2 ÷÷ – Ця величина становить статичний
8 è
ø
h ø
1
момент Aпрямокутника
2
h
max 0
2
2. При y 0 max
3. Для двутаврового профілю:
Побудуємо епюри розподілу дотичних і нормальних напружень для
двотаврової балки, і запишемо вирази для визначення дотичних напружень в точках
2' і 2', а також точки 3.
æ
2
4 y2 ö
Q
Q
, то відповідно, що cep çç 1 - 2 ÷÷ звідки:
3
b h Aпрямокутника
h ø
è
1. При y
D 2 2 D D 3
8
3 12
такими будуть дотичні напруження при умові, що розподіляються вони рівномірно
цих точках на цьому рівні.
Q
Sz
;
3
3Q
cep
.
2
2bh
2'
æh t ö
æh t ö
Q b t ç - ÷
Q b t ç - ÷
2 2ø
è
è 2 2ø ;
; 2''
( 3 )max номынальне ,
b Iz
d Iz
де – теоретичний коефіцієнт концентрації напруження.