Similar presentations:
Опір матеріалів. Розрахунково-графічні завдання з прикладами розрахунків. Частина 1
1.
Міністерство освіти і науки УкраїниВінницький національний технічний університет
В.А. Огородніков, О.В. Грушко, М.І. Побережний
ОПІР МАТЕРІАЛІВ
РОЗРАХУНКОВО-ГРАФІЧНІ ЗАВДАННЯ
З ПРИКЛАДАМИ РОЗРАХУНКІВ
Частина 1
Затверджено Ученою радою Вінницького державного технічного
університету як навчальний посібник для студентів всіх спеціальностей
денної форми навчання. Протокол №9 від 24 квітня 2003 р.
Вінниця ВНТУ 2003
2.
УДК 531: 620 (075)О 39
Рецензенти:
П.С. Бернік, доктор технічних наук, професор
І.О. Сивак, доктор технічних наук, професор
В.О. Федотов, кандидат технічних наук, професор
Рекомендовано до видання Ученою радою Вінницького державного
технічного університету Міністерства освіти і науки України.
Огородніков В.А., Грушко О.В., Побережний М.І.
О 39 Опір матеріалів. Розрахунково-графічні завдання з прикладами
розрахунків. Частина 1.
Навчальний посібник. – Вінниця: ВНТУ, 2003. – 158 с.
Посібник призначений для студентів усіх спеціальностей
денної форми навчання, що вивчають опір матеріалів.
УДК 531:620(075)
В.А. Огородніков, О.В. Грушко, М.І. Побережний, 2003
2
3.
ЗМІСТПередмова………………………………………………………………………5
Порядок та основні вимоги до виконання роботи……………...……………5
1 Епюри внутрішніх силових факторів………………………………………7
1.1 Короткі теоретичні відомості………………………………………7
1.1.1 Внутрішні сили. Метод перерізів…………………………….7
1.1.2 Епюри внутрішніх зусиль…………………………………….9
1.1.3 Диференціальні залежності між q, Q та M………………….10
1.1.4 Побудова епюр Q і М для двоопорних балок ……………...11
1.1.5 Побудова епюр Q і М для консольних балок ……………...15
1.1.6 Побудова епюр внутрішніх зусиль для плоских рам………19
1.1.7 Побудова епюр для кривих стержнів……………………….22
1.2 Завдання до розрахунково-графічної роботи ……………………26
2 Розтяг (стиск). Статично невизначувані системи при розтягу (стиску)…42
2.1 Короткі теоретичні відомості……………………………………...42
2.1.1 Напруження при осьовому розтягу (стиску)……………….42
2.1.2 Деформації при осьовому розтягу (стиску)………………...42
2.1.3 Закон Гука при розтягу (стиску)…………………………….43
2.1.4 Статично невизначувані задачі ……………………………..44
2.1.5 Розрахунки на міцність за допустимими напруженнями….45
2.2 Завдання до розрахунково-графічної роботи ……………………46
3 Напружено-деформований стан в точці…………………………………...56
3.1 Короткі теоретичні відомості……………………………………...56
3.1.1 Поняття про напружений стан………………………………56
3.1.2 Плоский напружений стан…………………………………...57
3.1.3 Головні площадки і головні напруження …………………..58
3.1.4 Коло напружень………………………………………………59
3.1.5 Узагальнений закон Гука…………………………………….61
3.1.6 Потенціальна енергія деформації…………………………...62
3.2 Завдання до розрахунково-графічної роботи ……………………64
4 Геометричні характеристики плоских перерізів………………………….72
4.1 Короткі теоретичні відомості……………………………………...72
4.1.1 Статичний момент площі. Центр ваги перерізу……………72
4.1.2 Моменти інерції перерізу……………………………………73
4.1.3 Формули переходу до паралельних або повернутих осей...74
4.1.4 Головні осі інерції та головні моменти інерції перерізу…..75
4.1.5 Радіуси інерції. Моменти опору…………………………….77
4.2 Завдання до розрахунково-графічної роботи ……………………78
5 Кручення…………………………………………………………………….85
5.1 Короткі теоретичні відомості……………………………………..85
5.1.1 Напруження і деформації при крученні стержнів
круглого поперечного перерізу……………………………………85
5.1.2 Епюри крутних моментів……………………………………87
3
4.
5.1.3 Розрахунки на міцність і жорсткість……………………….885.2 Завдання до розрахунково-графічної роботи ……………………90
6 Згин…………………………………………………………………………..98
6.1 Короткі теоретичні відомості……………………………………..98
6.1.1 Основні поняття……………………………………………...98
6.1.2 Напруження при чистому згині……………………………..98
6.1.3 Поперечний згин. Дотичні напруження…………………...102
6.1.4 Аналіз напруженого стану при згині. Розрахунки
на міцність…………………………………………………………103
6.1.5 Рівняння пружної лінії зігнутої балки……………………..105
6.1.6 Визначення кутових та лінійних переміщень методом
початкових параметрів…………………………………………..106
6.2 Завдання до розрахунково-графічної роботи …………………..108
Література……………………………………………………………………121
Додаток А Оформлення розрахунково-графічної роботи……………….122
Додаток Б Інструкції до написання програм та приклади побудови
епюр для балки та криволінійного стержня…………………124
Додаток В Інструкція до розрахунків геометричних характеристик
перерізу в середовищі КОМПАС ……………………………131
Додаток Г Повний розрахунок балки на міцність та жорсткість
в середовищі MATHCAD……..……………………………….…134
Додаток Д Сортамент прокатної сталі………………………………….…141
Додаток Е Програма мінімум до складання іспиту……………………....153
Додаток Ж Механічні характеристики матеріалів………………………..157
4
5.
ПЕРЕДМОВАЦей навчальний посібник написаний із врахуванням багаторічного
досвіду викладання курсу опору матеріалів у Вінницькому державному
технічному університеті. Він відрізняється від більшості посібників,
виданих раніше іншими авторами конспективним викладенням матеріалу,
наявністю 150 варіантів задач до кожного розділу із типовими
розрахунками та застосуванням сучасної обчислювальної техніки.
Особливістю посібника є і те, що до деяких задач пропонуються
інструкції до написання програм-документів із застосуванням пакетів
програм “КОМПАС 5.Х”, “Mathcad 200Х” в середовищі “Windows 9X” та
більш пізніх версій. Інструкції розраховані на студентів із початковим
рівнем знань користувача названих програмних продуктів.
В посібнику розкриті такі важливі для студентів машинобудівних та
будівельних вищих навчальних закладів розділи, як внутрішні зусилля,
геометричні характеристики плоских перерізів, напружений стан в точці,
прості види деформацій. Автори прагнули створити посібник максимально
корисний студентам не тільки при вивченні дисципліни, але й в курсовому
та дипломному проектуванні. Кожне із завдань ілюстроване детальним
прикладом розрахунку із поясненнями при розв’язуванні задачі.
ПОРЯДОК ТА ОСНОВНІ ВИМОГИ ДО ВИКОНАННЯ РОБОТИ
З дисципліни “Опір матеріалів”
студенти виконують три
розрахунково-графічні роботи (РГР). Іх зміст:
РГР№1 – Задачі 1, 2;
РГР№2 – Задачі 3, 4;
РГР№3 – Задачі 5, 6.
РГР мають бути оформлені у відповідності з діючими стандартами
ЄСКД(2.105 і 2.106 для текстових конструкторських документів та 2.104 –
для основних надписів). Розрахунково-графічні роботи виконуються на
аркушах формату А4 (210×297мм) основним креслярським шрифтом
(стандарт 2.304-68) з висотою літер не менше 2,5 мм, машинописним або
на принтері ЕОМ (Times New Roman 14 пт, одинарний інтервал) на одній
стороні аркуша. Перша сторінка протоколу оформляється у відповідності
зі стандартом 2.105-95; на наступних сторінках повинен бути штамп у
відповідності зі стандартом 2.104-68 (додаток А). На титульній сторінці
вказують номер розрахунково-графічної роботи, назву дисципліни,
прізвище та ініціали студента, варіант, факультет і групу.
Як виняток допускається текст роботи писати каліграфічним
розбірливим почерком пастою або чорнилом синього чи чорного кольору.
При необхідності виправити помилку, неправильний символ
закреслюють, а над ним пишуть виправлення. Допускається застосування
коректору.
5
6.
На одній сторінці допускається не більше трьох виправлень.Розв‘язання кожної задачі потрібно починати на новому аркуші так,
щоб розрахункова схема та формули, складені за нею, знаходились поряд.
На початку сторінки пишеться номер завдання, варіант і приводиться
повна та коротка умова задачі (що відомо та що потрібно знайти).
Розрахункові схеми (рисунки) виконують за допомогою креслярських
приладів або відповідних графічних програм. Розрахунки необхідно
супроводжувати короткими поясненнями.
Після зарахування усіх задач студент повинен до іспиту захистити
роботу.
Вибір варіанта завдання здійснюється за двома останніми цифрами
номера залікової книжки, які визначають номер рисунка розрахункової
схеми (див. табл.), перша цифра з кінця – варіант чисельних даних в
таблиці, приведеної в кожній задачі окремо.
Таблиця 1 – Вибір варіанта завдання
Схема
Останні дві цифри номера залікової книжки
00
00
15
30
45
60
75
01
01
16
31
46
61
76
02
02
17
32
47
62
77
03
03
18
33
48
63
78
04
04
19
34
49
64
79
05
05
20
35
50
65
80
06
06
21
36
51
66
81
07
07
22
37
52
67
82
08
08
23
38
53
68
83
09
09
24
39
54
69
84
10
10
25
40
55
70
85
11
11
26
41
56
71
86
12
12
27
42
57
72
87
13
13
28
43
58
73
88
14
14
29
44
59
74
89
90
91
92
93
94
95
96
97
98
99
Наприклад: номер залікової книжки ...23.
Номер схеми рисунка – 08. Варіант чисельних даних в таблиці – 3.
Шифр варіанта – 308.
Приклад шифру в основному надписі.
ОМ.1Б-01.З1.208
Студенти, що не виконали або не захистили хоча б одну
розрахунково-графічну роботу не допускаються до іспиту з дисципліни
"Опір матеріалів". В додатку Е приведена конспективно програма-мінімум
знань, якими студенти повинні обов’язково володіти для складання іспиту
на позитивну оцінку.
6
7.
1 ЕПЮРИ ВНУТРІШНІХ СИЛОВИХ ФАКТОРІВ1.1 Короткі теоретичні відомості
1.1.1 Внутрішні сили. Метод перерізів
У будь-якому тілі між його мікрочастинками завжди існують сили
взаємодії, які зумовлюють існування тіла як єдиного цілого.
При дії на тіло зовнішніх сил у будь-якому його перерізі виникають
додаткові, внутрішні сили взаємодії між частинками тіла (крім тих, що
існували в цьому елементі, коли він був ненавантажений), які
перешкоджають зміні відстаней між цими частинками і руйнуванню тіла.
Ці сили часто називають внутрішніми силами пружності. Саме внутрішні
сили і визначають для розрахунку на міцність та жорсткість бруса.
Для встановлення величини внутрішніх сил, що виникають у перерізі
Рисунок 1.1
стержнів, які підлягають зовнішній силовій дії, використовується метод
перерізів. Нехай є деяке пружне тіло (рисунок 1.1, а), що перебуває у
r r r r
рівновазі під дією системи зовнішніх сил P1, P2 , P3 , P4 . Розділимо це тіло
деякою площиною Н на дві частини Ι і ΙΙ. Відкинемо одну з частин,
наприклад Ι і розглянемо умови рівноваги частини ΙΙ (рисунок 1.1, б), що
залишилася. Щоб ця частина була в рівновазі, як і у випадку, коли вона
була частиною цілого тіла, треба, щоб крім зовнішніх сил, прикладених до
неї, були збережені й раніше діючі на цю частину внутрішні сили
взаємодії, що виникають між частинами Ι і ΙΙ під впливом зовнішніх сил.
Згадані внутрішні сили, суцільно розподілені по зробленому
перерізу, очевидно, можна звести до деякої системи сил, яка замінює вплив
відкинутої частини тіла на ту, що залишилася.
Якби ми розглядали рівновагу частини Ι, відкинувши частину ΙΙ, то
7
8.
вплив відкинутої частини, очевидно, врахувався б такими самимивнутрішніми силами, прикладеними до частини Ι у тому самому перерізі,
але у зворотному до попереднього напрямку.
У найбільш загальному випадку систему внутрішніх сил можна
r
r
звести до однієї сили R (головного вектора) і однієї пари сил M
(головного моменту).
При визначенні внутрішніх сил в стержнях рекомендується
проводити переріз перпендикулярно до осі стержня. Виберемо осі
координат x, y, z з початком в центрі ваги перерізу так,r щоб осі Oy і Oz
лежали в його площині. Розкладемо головний вектор
r R на складові по
осях координат: N ,Q y ,Q z , а головний момент M − на три моменти:
M x , M y і M z (рисунок 1.1, б).
Ці шість зусиль можуть бути легко знайдені з рівнянь рівноваги
(рівнянь статики), записаних для будь-якої із частин
n
n
∑ Pyi + Q y = 0 ,
∑ m yi + M y = 0 ,
i =1
n
i =1
n
i =1
n
i =1
n
i =1
i =1
∑ Pzi + Q z = 0 ,
∑ m zi + M z = 0 ,
∑ Px i + N = 0 ,
(1.1)
∑ mxi + M x = 0 ,
де Pyi , Pzi , Pxi − проекції зовнішніх сил на відповідні осі; myi , mzi , mxi −
моменти зовнішніх сил відносно відповідних осей.
Шість величин N, Qy , Qz , Mx , My i Mz прийнято називати
внутрішніми силовими факторами або внутрішніми зусиллями. Кожна із
цих сил має свою назву. Силу N, що діє вздовж осі x, називають
поздовжньою або нормальною силою. Сили Qy i Qz
називають
поперечними силами (рідше – силами, що перерізують) . Моменти My i Mz ,
очевидно , намагатимуться зігнути стержень у площинах xОy i xОz, тому їх
називають згинальними, а момент Mx , який скручує стержень, називають
крутним
Длямоментом
зусиль і моментів
.
у перерізі можна дати такі визначення:
поздовжня сила N – це сума проекцій усіх внутрішніх сил, що діють у
перерізі на нормаль до перерізу (чи на вісь стержня);
поперечні сили Qy, Qz – це суми проекцій усіх внутрішніх сил у перерізі на
головні центральні осі перерізу у и z відповідно;
крутний момент Мх (чи Мкр) – це сума моментів усіх внутрішніх сил у
перерізі щодо осі стержня;
згинальні моменти Му і Мz – це суми моментів усіх внутрішніх сил у
перерізі щодо головних центральних осей перерізу у и z відповідно.
Кожне з цих зусиль чи моментів, як уже вказувалося, є результатом
взаємодії частин розсіченого тіла, а тому повинно бути представлене у
вигляді двох протилежно направлених, але рівних векторів чи моментів.
Сукупність величин N, Qy, Qz і т.д., прикладених до правої сторони
8
9.
перерізу, заміняє дію вилученої лівої частини стержня на праву частину;сукупність зусиль і моментів, прикладених до лівої сторони перерізу,
виражає дію правої частини стержня на ліву.
Для практичного обчислення зусиль і моментів у перерізі варто мати
на увазі таке: N чисельно дорівнює алгебраїчній сумі проекцій на вісь
стержня (на нормаль до перерізу) усіх зовнішніх сил, що діють на одну з
частин (ліву чи праву) розсіченого стержня; Qy – те ж, але на вісь у, Qz – те
ж, але на вісь z; Мкр чисельно дорівнює алгебраїчній сумі моментів щодо
осі стержня всіх зовнішніх сил, що діють на одну з частин (ліву чи праву)
розсіченого стержня; Му – те ж щодо осі у, Mz – те ж, але щодо осі z. До
цього висновку легко прийти, якщо розглянути рівновагу кожної з частин
розсіченого стержня. При цьому сума проекцій (чи моментів) сил,
розташованих ліворуч від перерізу, повинна бути прикладена до правої
сторони перерізу і навпаки.
1.1.2 Епюри внутрішніх зусиль
Метод перерізів дозволяє знайти всі зусилля і моменти в будь-якому
перерізі стержня при дії будь-якого навантаження. Для цього потрібно:
а) знайти головні центральні осі поперечних перерізів стержня;
б) уявно провести поперечний переріз стержня в тому місці, де потрібно
знайти зусилля і моменти;
в) обчислити сили N, Qy, Qz і моменти Мкр, Му, Мz як алгебраїчні суми
проекцій і моментів зовнішніх сил, що діють на одну з частин (ліву чи
праву відносно перерізу) розсіченого стержня (звичайно на ту, де
проекції і моменти обчислюються простіше).
Для того, щоб поперечна сила і згинальний момент, визначені з
розгляду лівої та правої частин балки, були однакових знаків, слід
дотримуватися певного правила знаків.
Поперечну силу Q в перерізі будемо вважати додатною, якщо вона
намагається повернути вирізаний елемент за стрілкою годинника (рисунок
1.2, а). Згинальний момент M (для горизонтальних прямолінійних ділянок)
будемо вважати додатним, якщо він вигинає балку опуклістю вниз
(стиснуті верхні волокна) (рисунок 1.2, а). Поздовжню силу N в перерізі
будемо вважати додатною, якщо її вектор направлений від перерізу
(викликає деформацію розтягу). Крутний момент Мкр вважається
додатним, якщо при спостеріганні з торця вздовж осі частини, що
розглядається, він діє за годинниковою стрілкою (рисунок 1.3).
Зусилля і моменти в різних перерізах одного й того ж стержня різні.
Графіки (діаграми), що показують, як змінюються внутрішні
зусилля при переході від перерізу до перерізу, називають епюрами.
Відзначимо деякі правила, які застосовуються при побудові епюр:
а) вісь (базу), на якій будується епюра, завжди вибирають так, щоб вона
була паралельна чи просто збігалася з віссю стержня;
9
10.
б) ординати епюри відкладають від осі епюри по перпендикуляру;в) штрихувати епюри прийнято лініями, перпендикулярними до бази;
г) для зусиль і моментів вибирають деякий масштаб. Ординати
відкладають в масштабі. Крім того, на епюрах проставляють числа, що
показують величини характерних ординат, а в полі епюри в кружках
ставлять знак зусилля.
Рисунок 1.2
Рисунок 1.3
1.1.3 Диференціальні залежності між q, Q та M
Нехай на прямолінійний
стержень в деякій площині хОу
діє
зрівноважена
система
зосереджених сил, зосереджених
моментів та розподілених сил q
напрямок яких не збігається з
віссю
стержня.
Тоді
диференціальні залежності між
інтенсивністю
розподіленого
Рисунок 1.4
навантаження q, поперечною
силою Q і згинальним моментом M будуть мати вигляд (теореми
Журавського)
dQ y
= q.
dx
dM z
= Qy .
(1.2)
dx
d 2M z
= q.
dx 2
З рівнянь (1.2) випливають такі правила, що застосовують для
перевірки правильності побудови епюр:
10
11.
а) на тих ділянках, де немає розподіленого навантаження, епюра Q обмежена прямими, паралельними базі, а епюра М, у загальному випадку —похилими прямими;
б) на тих ділянках, де до балки прикладене рівномірно розподілене
навантаження, епюра Q обмежена похилими прямими, а епюра М —
квадратичними параболами. При побудові епюри М на стиснутих
волокнах опуклість параболи звернена убік, протилежну напрямку дії
навантаження q;
в) у тих перерізах, де Q = 0, дотична до епюри М паралельна осі епюри;
г) на ділянках, де Q>0, М зростає, де Q < 0, М спадає.
д) у тих перерізах, де до балки прикладені зосереджені сили на епюрі Q
будуть стрибки на величину й у напрямку прикладених сил, а на епюрі
М будуть злами;
е) у тих перерізах, де до балки прикладені зосереджені моменти, на епюрі
М будуть стрибки на величину цих моментів, на епюрі Q змін не буде.
1.1.4 Побудова епюр Q і М для двоопорних балок
Побудову епюр Q та M для балок починають з визначення повної
системи навантажень, в яку входять як задані сили, так і опорні реакції,
тобто визначають реакції опор. Після визначення опорних реакцій та їх
перевірки балку розбивають на ділянки. При цьому керуються правилом,
що граничними точками ділянок є точки прикладення зосереджених сил,
зосереджених моментів, а також точки змінювання інтенсивності
розподіленого навантаження.
Далі, використовуючи метод перерізів, будують епюри Q та M на
кожній ділянці балки, з врахуванням основних правил побудови епюр (див.
п. 1.1.2).
З практичної сторони, стосовно балок, часто користуються такими
правилами, які слідують із вищевстановлених:
а) поперечна сила Q в перерізі балки чисельно дорівнює алгебраїчній сумі
проекцій на вертикальну вісь перерізу всіх сил, що діють по одну
сторону від нього
n
Q y = ∑ Pyi відсіч .
i =1
В праву частину записуються проекції зовнішніх сил з врахуванням
такого правила знаків: якщо зовнішня сила намагається повернути
відсічену частину балки відносно перерізу, що розглядається, за
годинниковою стрілкою, то вона береться зі знаком “+” (рис. 1.5, а; 1.2).
б) згинальний момент М в перерізі балки чисельно дорівнює алгебраїчній
сумі моментів відносно центра ваги перерізу всіх сил, що розташовані по
одну сторону від цього перерізу.
11
12.
nM z = ∑ m zi відсіч .
i =1
В праву частину записуються моменти зовнішніх сил з врахуванням
такого правила знаків: якщо зовнішня сила (або момент чи розподілене
навантаження)
створює
такий
згинальний момент,
що
викликає
деформації стиску в
верхніх
волокнах
балки
відносно
перерізу, то він
береться зі знаком
“+” (рис. 1.5, б; 1.2).
Рисунок 1.5
Приклад. Побудуємо епюри поперечних сил і згинальних моментів
для балки, показаної на рисунку 1.6, а.
Спочатку визначимо реакції опор RA i RK із рівнянь рівноваги статики
(в опорі А горизонтальна складова реакції RA дорівнює нулю, оскільки в
системі відсутні сили, що проектуються на вісь стержня):
ΣМА = 0;
M1 – Р1⋅1 + Р2⋅2 – q⋅3(2 + 3/2) – M2 + Rк⋅5 = 0;
ΣМА = 4 − 1 ⋅1 + 3 ⋅ 2 − 2 ⋅ 3 ⋅ 3,5 − 3 + R K ⋅ 5 = 0 ;
Rк = 3 кН.
ΣМК = 0;
M1 – RА⋅5 + Р1⋅4 – Р2⋅3 – q⋅3(3/2) – M2 = 0;
ΣМК = 4 − R A ⋅ 5 + 1 ⋅ 4 − 3 ⋅ 3 + 2 ⋅ 3 ⋅1,5 − 3 = 0 ;
RА = 1 кН.
Перевірка:
∑Y = RА – Р1 + Р2 – q⋅3 + Rк = 1 − 1 + 3 − 2 ⋅ 3 + 3 = 0 .
Отже, реакції розраховані правильно.
Розділяємо балку на чотири ділянки і складаємо рівняння
поперечних сил та згинальних моментів для кожної з них.
Побудуємо епюри Qy i Mz для ділянки АВ. Для цього зробимо переріз
m1−n1 на відстані х від опори А і розглянемо рівновагу відсіченої частини
(рисунок 1.6, г). Згинальний момент Mz і поперечну силу Qy в перерізі
будемо зображати додатними.
Ділянка АВ.
0 ≤ x1 ≤ 1 м.
Qy(x1) = RA = 1 кН;
(1.3)
Mz (x1) = RA⋅x1 − M1 = x1 − 4;
(1.4)
при x1=0 м Mz (0) = −4 кН⋅м,
12
13.
при x1=1 м Mz(1) = 1−4 = –3 кН⋅м.Як видно із рівнянь (1.6) і (1.7) поперечна сила залишається сталою
на всій довжині ділянки АВ, а згинальний момент змінюється за лінійним
законом. Графіки цих залежностей показані на рисунках 1.6, б та 1.6, в.
Додатні значення сили Qy будемо відкладати вгору від базової прямої, а
від’ємні − вниз. Епюри згинальних моментів будуємо на стиснутих
волокнах. Тому вгору від базової лінії будемо відкладати в масштабі
додатні значення згинального моменту, а вниз − від’ємні.
Рисунок 1.6
Вказівка. При побудові епюр згинальних моментів на розтягнутих
волокнах додатні значення згинального моменту відкладаються
вниз, а вверх – від’ємні).
13
14.
Побудуємо епюри Мz i Qy для ділянки ВС. Для цього зробимо перерізm2−n2 і розглянемо рівновагу лівої відрізаної частини балки (рис. 1.6, д)
Ділянка ВС
0 ≤ x2 ≤ 1 м;
Qy(x2) = RA − P1 = 1−1 = 0 кН;
Mz(x2) = RA(1+x2) − P1x2 − M1 = 1(1+x2) − 1⋅x2 − 4 = –3 кН⋅м.
Будуємо графіки епюри Qy і Mz на ділянці ВС (риc. 1.6, б, в).
Із умов рівноваги лівої відсіченої частини балки знаходимо закони,
за якими змінюються Qy i Mz на ділянці CD.
Ділянка CD
0 ≤ x3 ≤ 1 м;
Qy(x3) = RA − P1 + P2 − qx3 = 3 – 2⋅x3;
qx 32
M z (x 3 ) = R A (2 + x 3 ) − M 1 − P1 (1 + x 3 ) + P2 x 3 −
=
2
= 1(2 + x3) – 4 – 1 (1 + x3) + 3x3 – 2⋅x32/2 = -3 + 3x3 – x32 ;
при x3 = 0 м Qy(0) = 3 кН;
Mz(0) = −3 кН⋅м;
при x3 = 1 м Qy(1) = 1 кН;
Mz(1) = −1 кН⋅м.
Для побудови епюр Qy i Mz на ділянці DK розглянемо рівновагу
правої відрізаної частини балки (переріз m3−n3 , рисунок 1.6, е)
Ділянка DK
0 ≤ x4 ≤ 2 м;
Qy(x4) = q⋅x4−RK = 2x4−3;
(1.5)
qx 42
M z (x 4 ) = RK x 4 −
= 3x4 – x42 ;
(1.6)
2
при x4 = 0 м Qy(0) = –3 кН;
Mz(0) = 0 кН⋅м;
при x4 = 2 м Qy(2) = 1 кН;
Mz(2) = 2 кН⋅м.
Епюра Qy(x4) перетинає вісь х, (рис. 1.6, б), це означає що в точці
перетину момент Mz набуде екстремального значення. Знайдемо цю точку
із умови
Qy(x4) = 0, або 2x4−3 = 0, звідки
R
3
x 4 = K = = 1,5 м.
q
2
Величина згинального моменту при х4 = 1,5 м,
M z (1.5 ) = 3x4 – x42 = 3⋅1,5 – 1,52 = 2,25 кН⋅м.
Будуємо епюри Qy i Mz на ділянці DK (рис. 1.6, б, в).
Перевірка епюр (п. 1.1.3, правила а) – е)).
Як видно із рисунків 1.6, б, в на ділянках, де немає розподіленого
14
15.
навантаження (q=0), поперечна сила Qy залишається сталою, а момент Mzзмінюється за лінійним законом (ділянка АВ). На ділянці ВС Qy=0, а
Mz=const. На ділянках CD та СК з рівномірно розподіленим навантаженням
(q=const), епюра Qy − лінійна (вираз 1.5), а згинальний момент Mz
змінюється за законом квадратичної параболи (вираз 1.6).
Оскільки епюра Mz побудована на стиснутих волокнах, то опуклість
параболи звернена убік протилежний напрямку дії навантаження q
(ділянки CD та СК).
Вказівка. При побудові епюр згинальних моментів на розтягнутих
волокнах опуклість параболи звернена убік, що збігається з
напрямком дії навантаження q).
В перерізах, де прикладені зосереджені сили, на епюрі Qy мають
місце стрибки на величину цих сил в напрямку вектора сили, а на епюрі Mz
− злами.
В перерізах, де прикладені тільки зосереджені моменти, на епюрі Qy
змін немає, а на епюрі Mz мають місце стрибки на величину цих моментів.
На ділянках, де Qy = 0, момент Mz сталий, а в перерізах, де Qy = 0,
згинальний момент набуває екстремального значення.
В додатку Б наведена програма, інструкція до написання програми та
результати розрахунку приведеної вище задачі із застосуванням пакета
програм Mathcad 2000.
1.1.5 Побудова епюр Q і М для консольних балок
Балка, жорстко закріплена одним кінцем (рисунок
1.7) називається консольною.
На відміну від двоопорних балок, при побудові
Рисунок 1.7
епюр внутрішніх зусиль для консольних балок, опорні
реакції можна не визначати, проте необхідно рухатись
завжди від вільного кінця балки до защемлення. При відомих опорних
реакціях напрямок розгляду ділянок не має значення.
Всі інші правила та залежності при побудові Q і М для консольних
балок залишаються незмінними (див п. 1.1.3, 1.1.4).
Приклад. Скласти рівняння та встановити закони розподілу
поперечних сил і згинальних моментів для балок, показаних на рисунку
1.8, 1.9.
15
16.
qq
a
a
Рисунок 1.8
Рисунок 1.9
16
17.
qРисунок
1.8.
Розріжемо
балку
q(x)
довільним перерізом, що знаходиться G = q(x)⋅x/2
на відстані х від вільного кінця балки.
Значення розподіленого навантаження в
цьому перерізі визначимо через
подібність трикутників
x/3
q( x ) q
q
= , q(x) = x .
x
x
a
a
Поперечна сила Qy(x) чисельно
a
дорівнює площі трикутника, утвореного
Qy
його катетами q(x) та x. Ця сила 0
прикладена в центрі ваги трикутника –
x
qa/2
на відстані від його катета.
3
Вирази Qy(x) та Mz (x) запишемо із 0
Mz
врахування правил знаків
1
q
Qy(x) = -G = – q(x)⋅x = − x 2 ;
qa2/6
2
2a
1
x
x
q
Рисунок 1.10
Mz (x) = -G⋅ = – q(x)⋅x⋅ = − x 3 .
2
3
3
6a
G = q(x)⋅x/2
Отже, Qy(x)
змінюється по
квадратичній параболі, Mz (x) – по
кубічній (рисунок 1.10).
Рисунок 1.9. Задача зводиться до
попередньої. Додамо до прикладеного
до балки навантаження до рівномірно
q⋅x
розподіленого q. Для того, щоб схема
x/3
навантаження не змінилась, прикладемо
x
знизу
навантаження
протилежного
знака, так як показано на рисунку. Тепер
a
маємо
балку,
що
навантажена
Qy
рівномірно
розподіленим 0
навантаженням q = const та трикутним
навантаженням з вершиною на вільному
qa/2
кінці балки.
Вирази Qy(x) та Mz (x) будуть мати 0
Mz
вигляд із врахуванням
q 2
Qy(x) = G – q⋅x =
x – q⋅x;
2a
qa2/3
q 2
q 2
x
q 3
Mz (x) = G⋅ – x =
x – x .
Рисунок 1.11
2
3 2
6a
Рисунок 1.11 ілюструє характер
17
18.
змінювання Qy(x) та Mz (x).Приклад. Побудувати епюри поперечних сил і згинальних моментів
для консольної балки, показаної на рисунку 1.12, а.
Опорні реакції не визначаємо. Напрямок розгляду перерізів – від
точки А до защемлення.
Розділяємо балку на чотири ділянки і складаємо рівняння
поперечних сил Qy(x) та згинальних Mz (x) моментів для кожної з них. Для
трикутного розподіленого навантаження користуємось виведеними вище
залежностями.
Ділянка АВ
0 ≤ x1 ≤ 1 м.
q
2
Qy(x1) = − x 12 = − x 1 ,
2a
q
1
Mz (x1) = М − x 13 = − x 13 + 2,
6a
3
при x1=0 м Qy(0) = 0 кН,
Mz (0) = 2 кН⋅м,
при x1=1 м Qy(1) = -1 кН,
Mz (1) = 1,67 кН⋅м.
Ділянка ВС
0 ≤ x2 ≤ 1 м.
qa
Qy(x2) = −
− qx 2 = − 1 − 2 x 2 ,
2
2
qa 1
qx 2
2
Mz (x2) = М − a + x 2 −
= 1,67 – x 2 – x 2 ,
2 3
2
при x2 = 0 м Qy(0) = -1 кН,
Mz (0) = 1,67 кН⋅м,
при x2 = 1 м Qy(1) = -3 кН,
Mz (1) = -0,33 кН⋅м.
Ділянка CD
0 ≤ x3 ≤ 1 м.
qa
q
2
Qy(x3) = −
− qb − qx 3 + x 3 2 = − 3 − 2 x 3 + x 3 ,
2
2c
2
qa 1
q 3
1
qx 3
Mz (x3) = М − a + b + x 3 − qb b + x 3 −
+ x3 =
2 3
6c
2
2c
2 1
= -0,33 – 3 x 3 – x 3 + x 3 3 ,
3
при x3 = 0 м Qy(0) = -3 кН,
Mz (0) = -0,33 кН⋅м,
при x3 = 1 м Qy(1) = -4 кН,
Mz (1) = -4 кН⋅м.
18
19.
Ділянка DE0 ≤ x4 ≤ 1 м.
qa
qc
Qy(x4) = −
− qb − + P = 1 (кН),
2
2
qa 1
1
qc 2
Mz (x4) = М − a + b + c + x 4 − qb b + c + x 4 − c + x 4 + Р x 4 =
2 3
2
2 3
= -4 + x 4 ,
при x4 = 0 м Mz (0) = -4 кН⋅м,
при x4 = 1 м Mz (1) = -3 кН⋅м.
За отриманими значеннями, із врахуванням основних властивостей
епюр та рис. 1.10 та 1.11, будуємо епюри для заданої балки (рисунок 1.12)
Р = 5 кН
q = 2 кН/м
М = 2 кН⋅м
А
С
B
x1
x2
a = 1м
x3
b = 1м
a)
Е
D
x4
c = 1м
d = 1м
1
1
0 Qy , кН
0
1
б)
3
4
2
1,67
0
0
Mz , кН⋅м
0,33
в)
3
Рисунок 1.12
19
4
20.
2021.
1.1.6 Побудова епюр внутрішніх зусиль для плоских рам1м
1м
Рамами називають системи, що складаються з прямолінійних
стержнів, з'єднаних жорсткими вузлами. Вертикально розташовані стержні
рами прийнято називати стояками, горизонтальні — ригелями. Жорсткість
вузлів усуває можливість взаємного повороту скріплених стержнів, тобто у
вузловій точці кути між їх осями залишаються незмінними.
Вісь рами являє собою ламану лінію, однак кожну прямолінійну
ділянку її можна розглядати як балку. Тому, щоб побудувати будь-яку
епюру для рами, потрібно побудувати її для кожної окремої балки, що
входить до складу рами. На відміну від звичайних балок у перерізах
стержнів рами, крім згинальних моментів М та поперечних сил Q,
звичайно діють ще і поздовжні сили N. Отже, для рам потрібно будувати
епюри N, Q і М.
Для N і Q зберігаються раніше прийняті правила знаків:
N > 0, якщо поздовжні сили викликають розтягання;
Q > 0, якщо її вектори прагнуть обертати частини розсіченої рами
(відносно точок, близьких до перерізу) за годинниковою стрілкою.
Для згинальних моментів спеціального правила знаків не
встановлюють, а при складанні виразів для М (х) приймають за власним
розсудом який-небудь момент додатним.
Вирази для N (x), Q (х) і М (х) можна не записувати (при певному
досвіді побудови епюр) – за виключенням для тих ділянок, де діє
розподілене навантаження. Найчастіше просто обчислюють значення N, Q
і М в характерних перерізах (на межах ділянок і в екстремальних точках), а
потім проводять лінії епюр, з огляду на їхні властивості, відзначені в п.
1.1.3.
Ординати епюр, як і завжди, відкладаємо перпендикулярно до осі
рами, причому додатні ординати Q і N із зовнішньої сторони рами, а
від’ємні – з внутрішньої
(якщо, звичайно, рама
P 2 =3 кН
q=2 кН/м
такої конфігурації, що
можна
розрізнити
її
зовнішню і внутрішню
сторони).
Епюри
М
умовимося
для рам
P 1 =2 кН
M
будувати на стиснутих
волокнах.
Якщо рама має
більше однієї опори, то
°
°
перш ніж приступити до
°
2м
1м
побудови епюр, потрібно
методами статики знайти
опорні реакції.
Рисунок 1.13
21
22.
ПрикладПобудувати епюри внутрішніх силових факторів для рами, показаної
на рисунку 1.13. Вихідні дані P1 = 2 кН; P2 = 3 кН; М = 5 кН⋅м; q = 2 кН/м.
Розв’язування
Визначаємо реакції опор YA i XA i YВ із рівнянь рівноваги статики
(рис. 1.14, а):
ΣМА = 0;
–Р1⋅1 – q⋅2⋅1 – Р2⋅3 + M +YВ⋅2 = 0;
YВ = 0,5[2⋅1 – 2⋅2⋅1 – 3⋅3 + 5] = 5 кН;
YВ = 5 кН.
ΣМВ = 0;
-YА⋅2 – Р1⋅1 + q⋅2⋅1 + M – Р2⋅1 = 0;
YА = 0,5[–2⋅1 + 2⋅2⋅1 + 5 – 3⋅1] = 2 кН;
YА = 2 кН.
ΣFx = 0;
Р1 + XА = 0;
XА = -2 кН.
Перевірка:
ΣFу = YА – q⋅2 – Р2 + YВ = 2 – 2⋅2 – 3 + 5 = 0.
Отже, реакції розраховано правильно.
Оскільки при XА знак “–”, то дійсний напрямок реакції XА
направлений у протилежний бік до попередньо вибраного. Змінюємо
напрямок вектора XА (рис. 1.14, а).
Розділяємо раму на шість ділянок і складаємо рівняння поперечних
сил та згинальних моментів для кожної з них.
Ділянка АС
0 ≤ x1 ≤ 1 м.
N(x1) = -YA = -2 кН;
Qy(x1) = XA = 2 кН;
Mz (x1) = XA ⋅x1 = 2x1;
при x1=0 м Mz (0) = 0 кН⋅м,
при x1=1 м Mz(1) = 2⋅1 = 2 кН⋅м.
Ділянка СD
0 ≤ x2 ≤ 1 м.
N(x2) = -YA = -2 кН;
Qy(x2) = XA – P1 = 0 кН;
Mz (x2) = XA (1+ x2) – P1 x2 = 2 кН⋅м.
Ділянка DE
0 ≤ x3 ≤ 2 м.
N(x3) = 0 кН;
Qy(x3) = YA – q⋅x3 = 2 – 2⋅x3, (рівняння прямої лінії);
Mz (x3) = YA⋅x3 – 0,5⋅q⋅x32 = 2x3 – x32, (рівняння параболи);
при x3 = 0 м Qy (0) = 2 кН,
22
23.
Mz (0) = 0 кН⋅м,при x3 = 2 м Qy (2) = –2 кН,
Mz (2) = 2 кН⋅м.
P 2 =3 кН
q= 2 к Н / м
E
х3
F
х4
х6
х2
1м
D
C
H M = 5 кН
y В =5 кН
х5
yА = 2 к Н
хА
A
х1
1м
P 1 =2 кН
°B
° 1м
х А =2 к Н °
2м
N , кН
а)
Q , кН
2
3
3
2
1м
2
2
M , кН·м
3
2
б)
5
в)
2
M , кН·м
2
1м
5
2
1м
3
5
2
2
2
3
3
2
2
5
5
д)
г)
Рисунок 1.14
Епюра Qy(x3) перетинає вісь х, (рис. 1.14, в), це означає що в точці
перетину момент Mz набуде екстремального значення. Знайдемо цю точку
23
24.
із умовиQy(x4) = 0, або 2 – 2⋅x3 = 0, звідки x3 = 1 м.
Величина згинального моменту при х4 = 1м: Mz (1) = 2 – 22 = 2 кН⋅м.
Ділянка FE
0 ≤ x4 ≤ 1 м.
N(x4) = 0 кН;
Qy(x4) = P2 = 3 кН;
Mz (x4) = P2⋅x3 = 3x3 ;
при x4=0 м Mz (0) = 0 кН⋅м,
при x4=1 м Mz(1) = 3⋅1 = 3 кН⋅м.
Ділянка ВН
0 ≤ x5 ≤ 1 м.
N(x5) = -YВ = -5 кН;
Qy(x5) = 0;
Mz (x5) = 0.
Ділянка ВН
0 ≤ x6≤ 1 м.
N(x6) = -YВ = -5 кН;
Qy(x6) = 0;
Mz (x6) = М = 5 кН⋅м.
За отриманими значеннями, із врахуванням основних властивостей
епюр, будуємо епюри для рами (рисунок 1.14). Для прикладу епюра
згинальних моментів побудована на стиснутих (рис. 1.14 г) та розтягнутих
(рис. 1.14 д) волокнах.
1.1.7 Побудова епюр для кривих стержнів
Кривим стержнем (брусом) називається стержень, геометрична вісь
якого криволінійна.
Надалі будемо розглядати криві стержні, в яких:
а) геометрична вісь – плоска крива;
б) площина кривизни – площина симетрії;
в) діючі сили лежать в площині кривизни.
Внутрішні зусилля в поперечному перерізі бруса визначають
методом перерізів через зовнішні зусилля, що діють по одну сторону від
перерізу. В поперечних перерізах виникають в загальному випадку три
внутрішні силові фактори: поздовжня сила N, поперечна сила Q та
згинальний момент М.
В випадку, коли вісь кривого стержня являє собою дугу кола,
положення любого перерізу зручно визначати за допомогою полярної
системи координат, тоді поздовжня, поперечна сила та згинальний момент
будуть функціями кута ϕ – N(ϕ), сила Q(ϕ), М(ϕ).
Правила визначення N(ϕ), Q(ϕ), М(ϕ).
24
25.
Поздовжня сила N в вибраному перерізі дорівнює алгебраїчній суміпроекцій всіх зовнішніх сил, що розташовані по одну сторону від перерізу;
сили проектуються на дотичну до геометричної осі в вибраному перерізі.
Правило знаків N (збігається з правилом знаків для балок та рам):
якщо проекція зовнішньої сили направлена від перерізу (розтяг) то вона
береться зі знаком “+”, якщо до перерізу (стиск), то знак “–”.
Поперечна сила Q в вибраному перерізі дорівнює алгебраїчній сумі
проекцій всіх зовнішніх сил, що розташовані по одну сторону від перерізу;
сили проектуються на радіус кривизни, проведений до точки перерізу.
Правило знаків Q (збігається з правилом знаків для балок та рам):
якщо зовнішня сила намагається обертати відрізану частину стержня за
годинниковою стрілкою то її проекція береться зі знаком “+”, якщо проти
годинникової стрілки, то знак “–”.
Згинальний момент М в вибраному перерізі дорівнює алгебраїчній
сумі моментів всіх зовнішніх сил відносно центра ваги перерізу, при цьому
розглядаються моменти сил, що розташовані по одну сторону від перерізу.
Правило знаків М: якщо зовнішня сила намагається деформувати
відрізану частину стержня таким чином, що його кривизна буде
збільшуватись, то момент від цієї сили береться зі знаком “+”.
Диференціальні співвідношення між N(ϕ), Q(ϕ), М(ϕ) виводяться на
основі рівноваги елемента, виділеного з довільно навантаженого кривого
стержня. Вони мають вид (для випадку, коли рівномірно розподілене
навантаження відсутнє q = 0)
dN
dQ
dM
= −Q ,
=N,
= QR ,
(1.7)
dϕ
dϕ
dϕ
де R – радіус кривизни стержня в перерізі.
Основні правила перевірки правильності побудови епюр
залишаються такими ж, як і для балок та рам із врахуванням особливостей
диференціальних
залежностей (1.7).
Приклад
Побудувати
епюри
α2=3π/2
внутрішніх силових факторів
Р2= 10 кН
для криволінійного стержня,
показаного на рисунку 1.15.
М= 4 кН⋅м
2м
Вихідні дані P1 = 5 кН; P2 =
α=π/2
10 кН; М = 4 кН⋅м; R = 2 м, α
= π/2, α2 = 3π/2.
Р1= 5
Розв’язування
кН
Розділяємо стержень на
Рисунок 1.15
дві ділянки і складаємо
рівняння
поздовжніх,
поперечних сил та згинальних моментів для кожної з них (рис. 1.16).
25
26.
Ділянка АВ0 ≤ ϕ ≤ α;
N(ϕ) = –P1⋅cos(ϕ).
26
27.
Р2⋅cos(ϕ –α)ϕ –α
ϕ –α
С
Р2
В
М
α
R⋅cos(ϕ)
R
Р2⋅sin(ϕ –α)
ϕ
О
R[1-cos(ϕ)]
ϕ
Р1⋅cos(ϕ)
ϕ
а)
Р1
А
Р1
R⋅sin(ϕ –α)
Р2
Р1⋅sin(ϕ)
N , кН
Q , кН
2,5
0
4,33
2,5
2,5
4,33 5
4,33
4,33
2,5
5
0
0
5
5
2,5
5
4,33
4,33
2,5
б)
в)
0
M , кН⋅м
1
2,66
4
1
2,66
6
6
5
0
1,34
Рисунок 1.16
27
10
г)
28.
Q(ϕ ) = –P1⋅sin(ϕ);М(ϕ ) = –P1⋅R⋅[1 – cos(ϕ)].
або 0 ≤ ϕ ≤ π/2.
N(ϕ) = –5⋅cos(ϕ);
Q(ϕ ) = –5⋅sin(ϕ);
М(ϕ ) = –10⋅[1 – cos(ϕ)].
Ділянка ВС.
α ≤ ϕ ≤ α2.
N(ϕ) = –P1⋅cos(ϕ) – P2⋅sin(ϕ – α);
Q(ϕ ) = –P1⋅sin(ϕ) + P2⋅cos(ϕ – α);
М(ϕ ) = –P1⋅R⋅[1 – cos(ϕ)] + P2⋅R⋅sin(ϕ – α) + М.
або π/2≤ ϕ ≤ 3π/2.
N(ϕ) = –5⋅cos(ϕ) – 10⋅sin(ϕ – π/2);
Q(ϕ ) = –5⋅sin(ϕ) +10⋅cos(ϕ – π/2);
М(ϕ ) = –10⋅[1 – cos(ϕ)] + 20⋅sin(ϕ – π/2) + 4.
З інтервалом в π/6 (300) 0≤ ϕ ≤ 3π/2 знаходимо значення внутрішніх
силових факторів в перерізах (таблиця 1.1).
Таблиця 1.1
Ділянка АВ 0 ≤ ϕ ≤ π/2
Ділянка ВС π/2≤ ϕ ≤ 3π/2
0
0
0
0
0
0
30 60 90 90 1200 1500 1800 2100 2400 2700
-5 -4,33 -2,5 0
0 -2,5 -4,33 -5 -4,33 -2,5 0
N(ϕ) , кН
0 -2,5 -4,33 -5
5 4,33 2,5
0 -2,5 -4,33 -5
Q(ϕ), кН
-1 2,66 4 2,66 -1
-6
М(ϕ), кН⋅м 0 -1,34 -5 -10 -6
За отриманими значеннями будуємо на осі криволінійного стержня
епюри поздовжніх N(ϕ), поперечних сил Q(ϕ) та згинальних моментів
М(ϕ) (рисунок 1.16).
Ординати згинальних моментів відкладені в сторону стиснутих
волокон без вказівки знаку. При прийнятому правилі знаків ординати зі
знаком “+” до центра кривизни від осі стержня, “–” від центра кривизни від
осі стержня. При побудові на розтягнутих волокнах – навпаки.
Відкладаються ординати поздовжніх N(ϕ) та поперечних сил Q(ϕ) зі
знаком “+” на зовнішні стороні стержня, із обов’язковим указанням знака.
Перевірка епюр.
В точці А прикладена зосереджена сила Р1 по дотичній до осі
стержня, в цій точці на епюрі N(ϕ) – стрибок на величину цієї сили. На
епюрах Q(ϕ) та М(ϕ) в точці А стрибків немає. Графіки плавно виходять
із нуляВ. точці В прикладена зосереджена сила Р2, перпендикулярно до осі
стержня, та момент М. В цій точці на епюрі Q(ϕ) – стрибок на величину
сили Р2, на епюрі М(ϕ) – стрибок на величину момента М. На епюрі N(ϕ)
в точці В стрибків немає.
28
29.
Епюра Q(ϕ) перетинає нульову лінію (вісь стержня) двічі – в точці В,та при ϕ = 1800. В цих перерізах на епюрах N(ϕ) та М(ϕ) будуть
екстремальні точки (або дотична до епюр паралельна дотичній до осі
стержня в перерізі).
В додатку Б наведена програма, інструкція до написання програми та
результати розрахунку приведеної вище задачі із застосуванням пакета
програм Mathcad 2000.
1.2 Завдання до розрахунково-графічної роботи
Задача 1. Побудова епюр внутрішніх силових факторів
За заданими розрахунковими схемами побудувати епюри
відповідних внутрішніх силових факторів.*
План розв’язування задачі:
– визначити при необхідності опорні реакції (схеми б, г);
– записати для кожної ділянки рівняння, за якими будуються
відповідні епюри;
– розрахувати значення внутрішніх зусиль в характерних точках та
побудувати відповідні епюри.
Інші дані для розрахунків взяти з таблиці 1.2.
Таблиця 1.2
Варіант
1
2
3
4
5
6
7
8
9
0
q,
кН/м
1
1,5
2
2,5
3
1,5
1,5
2
2,5
3
Р1,
кН
5
4
3
2
1
5
4
3
2
1
Р2,
кН
1
2
3
4
5
1
2
3
4
5
М,
кН⋅м
2
1
3
2
3
1
1
2
3
2
а,
м
1
1,5
0,25
0,5
0,35
1
1,5
0,25
0,5
0,35
α ,°
15
30
45
60
75
15
30
45
60
75
* Користуйтесь прикладними програмами ПЕОМ для виконання
завдання (додаток Б)
29
30.
00P1
q
q
P2
а)
M
a
a
a
б)
P1
M
°
°
°
P2
a
a
a
2P 2
в)
a
а
P1
0 ,5 а
г)
°
°
M
3P 1
а
q
°
3а
2а
Рисунок 1.17
30
31.
01P1
P2
q
a
M
a
а)
a
P1
б)
M
°
°
°
a
P2
a
a
2P 2
a
в)
а
3P 1
q
P1
2а
°
°
q
M
°
2а
2а
Рисунок 1.18
31
г)
32.
02P1
а
а)
P2
q
M
а
а
б)
M
P2
°
°
°
P1
а
а
M
5а
a
P1
2а
1, 2 5 P 2
°
P1
Рисунок 1.19
32
г)
3а
q
5а
2а
в)
°
°
а
33.
03P1
P2
а)
q
M
а
а
а
P1
P2
б)
M
°
°
°
а
а
в)
а
г)
2а
M
а
1,5P 2
a
q
2а
2P 1
°
P2
0 ,5 a
°
°
1 ,5 a
Рисунок 1.20
33
34.
04M
P1
а
а)
P2
q
а
а
M
P2
°
°
°
P1
а
M
2а
q
2а
в)
г)
a
°
°
2а
а
3а
а
б)
1 .2 5 P 2
а
P1
P1
°
Рисунок 1.21
34
35.
05P1
P2
q
q
а)
M
a
a
a
P2
P1
M
б)
°
°
°
a
a
1,5a
a
г)
в)
2a
°
°
a
M
q
3a
2a
P1
°
P1
2P 2
Рисунок 1.22
35
36.
06P1
q
a
P2
M
q
a
а)
a
P1
M
°
б)
P2
°
°
a
г)
M
a
a
1,5a
в)
a
q
a
a
P1
a
a
2a
P2
1, 25P 1
P2
°
Рисунок 1.23
36
°
°
37.
P1q
а
07
P2
а)
M
а
а
б)
P1
M
P2
°
°
°
а
а
а
2P 2
a
в)
1,25P 1
q
P2
°
г)
M
3а
а
2а
а
°
°
2a
Рисунок 1.24
37
2P 1
38.
08P1
q
а)
M
a
P2
a
a
P2
P1
б)
M
°
°
°
a
a
2P 2
a
в)
г)
2a
2a
а
q
2а
P1
°
M
°
°
Рисунок 1.25
38
а
a
2P 1
39.
09P2
q
P1
q
а)
M
a
a
a
P1
M
P2
°
б)
°
°
a
a
a
в)
2P 2
a
3P 1
а
3а
г)
3а
°
q
°
°
M
а
P2
3а
Рисунок 1.26
39
40.
10P2
P1
q
а)
M
a
a
a
P2
M
P1
°
б)
°
°
a
a
a
P1
в)
а
г)
1,5P 1
4
3а
a
M
а
q
2P 2
°
a
Рисунок 1.27
40
°
°
41.
11q
P1
a
а)
P2
M
a
a
P1
P2
б)
M
°
°
°
a
a
a
г)
в)
а
3а
M
°
°
°
1 ,2 5 а
a
2а
q
P2
2а
2P 1
Рисунок 1.28
41
P2
42.
12M
P1
a
а)
P2
q
a
a
б)
P2
P1
M
°
°
°
a
a
a
г)
в)
0, 5P 1
P2
a
q
2а
а
а
a
M
°
°
3P 1
°
a
Рисунок 1.29
42
a
43.
13P1
P2
q
а
а)
M
а
а
P1
P2
M
°
б)
°
°
а
а
а
1,5P 2
в)
a
2а
1,25P 1
q
°
°
P2
M
°
а
а
Рисунок 1.30
43
а
г)
44.
14q
q
P1
a
P2
а)
M
a
a
P1
б)
M
°
°
°
P2
a
a
a
в)
г)
2P 2
°
a
q
a
a
1, 5а
2P 1
M
°
°
2а
1,5P 1
Рисунок 1.31
44
45.
2 РОЗТЯГ (СТИСК). СТАТИЧНО НЕВИЗНАЧУВАНІСИСТЕМИ ПРИ РОЗТЯГУ (СТИСКУ)
2.1 Короткі теоретичні відомості
2.1.1 Напруження при осьовому розтягу (стиску)
Центральний
(осьовий)
розтяг або стиск виникає від сил,
прикладених до осі бруса
(рисунок 2.1). Напружений стан,
що
спричиняється
такими
силами, називають простим або
лінійним (одновісним). В силу
гіпотези
плоских
перерізів
напруження
по
перерізу
розподіляються рівномірно, що
може бути виражено формулою
σ=
N
,
А
(2.1)
де
σ − нормальне напруження
в поперечному перерізі;
N − зусилля (нормальна сила) в
цьому перерізі;
A − площа перерізу.
Рисунок 2.1
2.1.2 Деформації при осьовому розтягу (стиску)
Уявимо прямий брус сталого поперечного перерізу A0 і довжиною l0
(рисунок 2.2). Під дією сили P брус видовжиться на деяку величину ∆ l
∆l = l − l0 ,
(2.2)
яку називають абсолютним видовженням.
При розтяганні бруса його поперечні розміри зменшуються. При
цьому абсолютна поперечна деформація дорівнюватиме
∆a = a − a0 .
(2.3)
Відношення абсолютного видовження ∆l до початкової довжини l0
називають відносним видовженням і позначають ε
45
46.
ε=∆l
l0
.
(2.4)
Аналогічно, відносна поперечна деформація дорівнює
ε' =
∆a
.
a
(2.5)
Зв’язок між відносною
поперечною
і
відносною
поздовжньою
деформаціями
виражається формулою
Рисунок 2.2
ε ' = − µε ,
(2.6)
де µ − безрозмірний коефіцієнт поперечної деформації − коефіцієнт
Пуассона. Знак “мінус” у формулі (2.6) говорить про те, що деформації ε' і
ε мають різні знаки, а коефіцієнт Пуассона визначається за формулою
ε'
µ=
.
(2.7)
ε
Величина µ для різних матеріалів неоднакова: так, для сталі µ=0.250.3, для каучуку µ=0.47. Значення µ для різних матеріалів приводяться в
довідниках.
2.1.3 Закон Гука при розтягу (стиску)
Напруження і деформації розтягу і стиску пов’язані між собою
залежністю, яку називають законом Гука, за ім’ям англійського фізика Роберта Гука (1635−1703), що встановив цей закон. Закон Гука справедливий
лише у певних межах навантаження і формулюється так: нормальне
напруження прямо пропорційне відносному видовженню або укороченню
σ = Eε .
(2.8)
Коефіцієнт пропорційності Е характеризує жорсткість матеріалу,
тобто його здатність протидіяти пружним деформаціям розтягу або стиску
і називається модулем поздовжньої пружності, модулем пружності
першого роду, модулем Юнга. Для сталі E = (1,8...2,2)⋅106 кг/см2 =
(1,8...2,2)⋅1011 Па = (1,8...2,2)⋅105 МПа.
З врахуванням (2.1) і (2.4) отримаємо другий закон Гука у формі
Nl
∆l =
.
(2.9)
EА
46
47.
За формулою (2.9) можна знайти деформацію ділянки стержнядовжиною l, якщо в межах цієї ділянки N і А сталі величини.
Повна деформація стержня, який має n ділянок дорівнює
N i li
.
i =1 E i Аi
n
∆l = ∑
(2.10)
Якщо нормальна сила N і площа перерізу А в межах ділянки l є
змінними величинами, то
l N ( x )dx
∆l = ∫
0
EА ( x )
.
(2.11)
Величина EА називається жорсткістю перерізу, а ЕА/l − жорсткістю
бруса. Чим більша площа А і менша довжина l бруса, тим більша його
жорсткість.
2.1.4 Статично невизначувані задачі
Пружна система (конструкція) є статично невизначуваною, якщо
зусилля в її елементах не можуть бути знайдені тільки із рівнянь статики.
Такі конструкції найбільш широко розповсюджені як більш жорсткі,
надійні і економічні в порівнянні зі статично визначуваними.
Ступінь статичної невизначуваності системи визначається
надлишком загального числа невідомих реакцій зовнішніх зв’язків і
внутрішніх зусиль по відношенню до числа незалежних рівнянь рівноваги ,
які можна скласти для даної системи. Ці “зайві” (в розумінні забезпечення
рівноваги системи і її геометричної незмінності) зв`язки накладають
додаткові обмеження на переміщення тих перерізів, біля яких вони
накладені
Визначення
.
всіх невідомих сил, тобто розкриття статичної
невизначуваності, можливе тільки шляхом складання рівнянь, що
доповнюють число рівнянь статики до числа невідомих. Ці додаткові
рівняння відображають особливості геометричних зв`язків, накладених на
деформовану систему. Вони можуть бути складені за допомогою уявлення
картини переміщень в конструкції, при її деформуванні і тому їх
називають рівняннями сумісності переміщень.
Методи
розрахунку
статично
невизначуваних
систем
підрозділяються в залежності від того, що приймається при розв`язанні
задачі за основні невідомі.
У разі, коли основними шуканими невідомими є зусилля в “зайвих”
зв`язках системи, метод носить назву методу сил. Якщо основними
невідомими є деформації або переміщення в системі, то розрахунок ведуть
за так званим методом переміщень. Тепер існує досить великий різновид
47
48.
цих основних і змішаних методів.Розв`язуючи рівняння переміщень сумісно з рівняннями статики,
можна визначити невідомі зусилля в елементах системи. Причому, якщо
система з жорсткими зв`язками, то рівняння сумісності переміщень
утворюють самостійну систему, а її розв`язання дає значення зайвих
невідомих. Якщо система має пружні зв`язки, то необхідно розв`язувати
сумісно рівняння переміщень і статики.
Розрахунки рекомендується проводити в такій послідовності:
- записати незалежні рівняння статики та встановити ступінь статичної
невизначуваності;
- скласти рівняння сумісності переміщень (число рівнянь сумісності
переміщень повинно дорівнювати ступеню статичної невизначуваності
системи)
- замінити деформації через зусилля за законом Гука (2.9);
- розв’язати отриману систему рівнянь, визначити внутрішні зусилля;
- розрахувати напруження або площі поперечних перерізів стержнів в
залежності від виду задачі.
2.1.5 Розрахунки на міцність за допустимими напруженнями
При розрахунках за допустимими напруженнями міцність
конструкції або її елементів буде забезпечена, якщо максимальне
напруження σmax не перевищує допустимого, тобто виконується умова
N
σ max ≤ [σ ],
σ max = ≤ [σ ] .
(2.12)
А
Якщо матеріал по різному чинить опір розтяганню і стисканню
(характерно для крихких матеріалів), то найбільші розтягувальні
напруження не повинні перевищувати допустимих напружень на
розтягання [σ]р , а найбільші стискувальні напруження − допустимих
напружень на стискання [σ]с. Формула (2.12) дає можливість розв’язувати
низку Проектний
інженернихрозрахунок
задач.
– підбір перерізу елементу конструкції при
відомих силах, що діють на елемент
N
А≥
.
(2.13)
[σ ]
Перевірний розрахунок, при якому визначають напруження і
порівнюють його з допустимим
N
σ max = ≤ [σ ] .
(2.14)
А
При перевірному розрахунку, як правило, визначають коефіцієнт
запасу міцності, з яким працює елемент.
Визначення допустимого навантаження на існуючий елемент
[N ] = [σ ]⋅ А .
48
(2.15)
49.
Умови міцності вимагають, щоб напруження, які виникають велементах конструкцій, не перевищували допустимих. Допустимі напруження [σ] становлять деяку частину від небезпечних напружень. Для
пластичних матеріалів таким небезпечним напруженням є границя
текучості σт , при якій деформації, що швидко зростають, перешкоджають
нормальній експлуатації конструкції. Для крихких матеріалів небезпечним
напруженням є границя міцності σв , при якій настає руйнування
матеріалу. Допустиме напруження визначають за формулою
σ
(2.20)
[σ] = nн ,
де σн = σт − для пластичних матеріалів і σн = σв − для крихких, n −
коефіцієнт запасу міцності при дії на конструкцію статичного
навантаження встановлюється в межах n = 1,5...2, для крихких − n = 3...5, а
іноді і вище (наприклад, для каменів природних і штучних він може бути в
межах n = 10...30). Коефіцієнт запасу міцності залежить також від умов
роботи конструкції, точності розрахунків напружень, характеру навантажень.
2.2 Завдання до розрахунково-графічної роботи
Задача 2. Розрахунок статично невизначуваних
розтягу (стиску) із пружними зв’язками
систем при
Абсолютно жорстка балка піддержується в горизонтальному
положенні пружними стальними стержнями згідно схеми (рис. 2.3 – 2.6).
Обчислити необхідну площу перерізів цих стержнів при заданому їх
співвідношенні.
Матеріали стержнів та співвідношення площ вказані на рисунку.
Інші дані для розрахунку взяти з таблиці.
Таблиця 2.1
Варіант
0
1
2
3
4
5
6
7
8
9
Р1, кН
10
12
14
16
18
20
22
24
25
11
а, см
90
85
80
75
70
65
60
55
70
50
49
50.
Сталь 20Г3a
Сталь
2A
A
10
2а
2а
00
5P
2.5а
Р
01
3А
Сталь
30Г
1.5a
Сталь
20Г
2a
А
2a
2a
3a
P
2А
Сталь
30Г
2P
02
А
Сталь
1.5a
2А
60
Сталь
3P
20Х
2a
а
P
А
2a
03
2А
4Р
Сталь
35
Сталь
40Х
а
а
1.5a
P
50
Рисунок 2.3
51.
А2a
Сталь
Сталь
a
45Х
1.5a
А
Сталь
04
2А
40ХН
20Г
a
1.5a
a
2P
3P
05
2А
35ХМ
50ХН
1.5А
a
Сталь
1.5a
2a
Сталь
А
Сталь
20Х
1.5a
2a
P
5P
06
А
2a
3a
Сталь
30
2А
Сталь
30ХМ
2a
2a
P
2P
Сталь
Сталь
A
25ХМ
2a
2a
2а
3а
3A
а
а
P
3P
51
Рисунок 2.4
2.5а
30Г
2A
Сталь
50ХН
07
52.
2aСталь
2А
35ХМ
40ХФА
Сталь 30Г
а 1.5а 1.5а
P
a
Сталь
08
А
2А
2a
3P
2А
А
Сталь
Сталь
50
40ХН
2a
2.5а
3.5a
09
1.5а
P
2P
2ХН3А
2.5a
45Х
2a
2a
2А
Р
3Р
P
3a
2А
Сталь
30ХГА
1.5a
Сталь
Сталь
10
2.5а
А
11
А Сталь
40ХН
2А
Сталь 45
2a
Рисунок 2.5
52
3а
3Р
53.
3Ра
2А
А
12
Сталь
Сталь
55
50
1.5a
P
2a
P
3a
13
А Сталь
40ХН
2А
Сталь 45
3а
2a
P
2.5а
А
Сталь 20Х
2a
14
2А
3a
1.5а
3P
3Р
Сталь
30
а
а
Рисунок 2.6
Рисунок 2.7
53
Приклад А. Жорстка балка
підтримується двома стержнями,
як показано на рисунку 2.7.
Перший стержень повинен мати
площу поперечного перерізу в два
рази більшу ніж другий; матеріал
стержнів – сталь 30Г. Визначити
площу поперечного перерізу
стержнів.
54.
Дано: а=1 м; b=2 м; с=1,5 м; α=45°; Р=120 кН; А1=2А2; Е1=Е2=Е.Визначити: А1−?; А2−?
Розв’язування. В задачі потрібно визначити площі перерізів стержнів,
тобто провести проектний розрахунок. Оскільки стержні системи
працюють на розтягання−стискання, то проектний розрахунок виконується
за формулою (2.13), а розв’язування задачі зводиться до визначення
нормальних сил в поперечних перерізах стержнів 1 і 2.
Статична сторона задачі
Використаємо
метод
перерізів і переріжемо стержні
поперечними
перерізами,
відкинемо
верхню
частину
стержня 1 і нижню частину
стержня 2, замінимо їх дію
нормальними силами N1 та N2.
Використовуючи
формальний
підхід, припустимо, що обидва
1
стержні
розтягнуті,
тобто
направимо N1 та N2 від перерізів.
Відкинемо також шарнір і
замінимо реакціями Rx
та Ry
2
(рисунок 2.8, а).
Для визначення чотирьох
невідомих реакцій N1 ,N2 ,Rx ,Ry ми
Рисунок 2.8
можемо
скласти
лише
3
незалежних рівняння статики, як для плоскої непаралельної системи сил,
тобто
∑ X = 0, ∑ Y = 0, ∑ M О = 0.
Отже, система один раз статично невизначувана.
Перші два рівняння статики крім N1 та N2 містять невідомі реакції Rx
та Ry, визначати які немає необхідності. Отже, відносно невідомих зусиль
N1 та N2 ми маємо лише одне рівняння:
o
(2.21)
∑ M м = P ( b + c ) − N 1 ( a + b + c ) sin 45 + N 2 ⋅ c = 0 .
Рівняння (2.21) містить дві невідомих величини. Для однозначного
розв’язання задачі необхідно знайти ще одне рівняння, що пов’язує N1 та
N2. Для цього необхідно скласти рівняння сумісності переміщень.
Геометрична сторона задачі
Розглянемо систему в деформованому стані.
За умовою задачі балка абсолютно жорстка, стержні 1 та 2 – пружні.
Нехай стержень 1 в результаті дії зовнішніх сил на систему видовжиться
на величину ∆l1.
Методом засічок визначимо положення балки ОВ’А’, яке відповідає
цьому видовженню (див рис. 2.8, б). Тоді стержень 2 набуде деформації
54
55.
стиску величиною -∆l2, тобто ВВ’ = −∆l2.Примітка. Балка закріплена в точці О шарнірно-нерухомою опорою, тому
вона може повернутись тільки за або проти годинникової стрілки відносно
точки О. Кут повороту балки нескінченно малий, тому вважається, що
точки А та В в процесі деформації системи рухаються по вертикалі, катет
АС в прямокутному трикутнику ∆АСА’ відповідає геометрично величині
∆l1, а кут при вершині А’ дорівнюватиме куту α (див. рис. 2.8).
Із трикутника ∆АСА’ маємо АС =∆l1,
АА’ = АС/ sin 45o = ∆l1/sin 45o.
(2.22)
Із подібності трикутників ∆ ОВВ’ ∞ ∆ ОАА’ випливає
АА ' a + b + c 4,5
=
=
= 3,
BB '
c
1,5
АА’=3ВВ’,
де ВВ’ = −∆l2.
З врахуванням (2.22) отримаємо рівняння сумісності переміщень
∆l1
sin 45
o
= −3∆l 2 .
(2.23)
Фізична сторона задачі
Виразимо ∆l1 та ∆l2 через зусилля в стержнях N1 та N2 у відповідності
до закону Гука (2.9)
∆l1 =
N1l1
;
EА1
Враховуючи, що А1=2А2, sin 45 o =
∆l1 та ∆l2 в рівняння (2.23)
∆l 2 =
N 2l2
.
EА2
2
a
, l1 =
, підставимо вирази для
2
sin 45 o
N1 ⋅ a⋅2 ⋅2
=−
N2 ⋅a
,
E ⋅ А2
3 ⋅E ⋅ 2 ⋅ А2 ⋅ 2
N1= −3N2.
Сумісним розв’язуванням рівнянь (2.21) та (2.25) визначаємо N1 та N2
P ( b + c ) + 3N 2 ( a + b + c ) cos 45 o + N 2 c = 0,
P ( b + c ) + N 2 [3( a + b + c ) cos 45 o + c] = 0,
55
(2.25)
56.
− P (b + c)− 120 ⋅103 ⋅ 3,5
3
N2 =
=
=
−
38
⋅
10
Н,
2
3( a + b + c ) cos 45 o + c
3 ⋅ 4,5 ⋅
+ 1,5
2
N1 = −3N2 = 114⋅103 Н.
Отримані знаки зусиль говорять про те, що при навантаженні
системи силою Р стержень 1 розтягується, а стержень 2 стискається. Порівняння величин N1 та N2 показує, що перший стержень більш навантажений. Проектний розрахунок стержнів
Визначаємо допустимі напруження. Допустиме напруження для
сталі 30Г (пластичний матеріал) дорівнює (формула 2.20)
[σ ] = σ н = σ т = 320 = 160 МПа,
n
n
2
де σн = σт = 320 МПа − границя текучості сталі 30Г (див. додаток Ж),
n − коефіцієнт запасу міцності при дії на конструкцію статичного
навантаження n = 1,5...2, приймаємо n = 2.
Таким чином [σ ]1 = [σ ]2 = 160 МПа.
Визначаємо необхідні площі А1, А1
N
114000
(2.26)
А1 ≥ 1 =
= 7,12 ⋅10 −4 м2 = 7,12 см2,
6
[σ ]1 160 ⋅10
N
38000
(2.27)
А2 ≥ 2 =
= 2.38 ⋅10 −4 м2 = 2,38 см2.
6
[σ ]2 160 ⋅10
За умовою задачі має виконуватись співвідношення А1 = 2А2. Нехай
А1 = S, тоді
А2 = S/2 ≥ 2,38, (з нерівності 2.27),
звідки S ≥ 4,76 см2,
А1 = S ≥ 7,12 см2, (з нерівності 2.26).
А
Остаточно приймаємо S = А1 = 7,2 см2, тоді А2 = 1 = 3,6 см2.
2
Розрахуємо робочі напруження в стержнях
N
114000
2
6
σ1 = 1 =
=
158
⋅
10
Н
/
м
=158 МПа< [σ]=160 МПа,
А1 7,2 ⋅10 −4
стержень 1 буде працювати із коефіцієнтом запасу n =
σ2 =
N2
А2
=
38000
3,6 ⋅10
−4
σ т 320
= 2,03.
=
σ 1 158
= 105,5 ⋅10 6 Н/м2 = 105,5 МПа< [σ] = 160 МПа.
стержень 2 буде працювати із коефіцієнтом запасу n =
σт
320
= 3,03.
=
σ 2 105.5
Таким чином, стержень 2 буде недовантажений при прийнятому
коефіцієнті запасу, що є нераціонально з точки зору економії матеріалу.
56
57.
Але надійність та жорсткість конструкції в цілому неодмінно збільшиться.Відповідь: А1 = 7,2 см2, А2 = 3,6 см2.
Приклад Б. Скласти рівняння сумісності деформацій для статично
невизначуваної системи, приведеної на рис. 2.9. а = 1 м, b = 2 м.
1
3 1
3
P1
A
b
a
A1
P2
B
C
D
F
B1
2
C1
2
Рисунок 2.9
Рисунок 2.10
Розв’язування.
Система, показана на рис. 2.9 один раз статично невизначувана. На
балку діють зовнішні сили Р1 та Р2 та сили реакцій стержнів N1, N2 та N3.
Балка знаходиться під дією системи плоскопаралельних сил, тому статична
сторона задачі вичерпується записом двох рівнянь, наприклад
∑Y = 0, ∑ M A = 0.
Отже, необхідно скласти лише одне рівняння сумісності деформацій.
Розглянемо систему в деформованому стані, що відповідає
кінематично можливому переміщенню (рис. 2.10).
За умовою задачі балка абсолютно жорстка, стержні 1, 2 та 3 –
пружні. Нехай стержень 1 в результаті дії зовнішніх сил на систему
видовжиться на величину ∆l1, а стержень 3 – видовжиться на величину ∆l3.
Методом засічок визначимо положення балки ОВ1А1, яке відповідає
цьому видовженню (див рис. 2.8, б). Тоді стержень 2 набуде деформації
стиску величиною -∆l2, тобто ВВ1 = −∆l2.
Примітка. Кінематично можливе переміщення балки складається із двох
переміщень: балка може опуститись (піднятись) на деяку відстань та
повернутись на певний кут. Обидва переміщення можна вважати
нескінченно малими в порівнянні із вихідними розмірами стержнів та
балки. Тому вважається, що точки А, В та С в процесі деформації системи
рухаються по вертикалі.
57
58.
Опустимо перпендикуляр із точки А1 на відрізок СС1. В результатіпобудови отримаємо два прямокутні трикутники ∆ А1DВ1 та ∆ А1FC1.
Із подібності трикутників ∆ А1DВ1 ∞ ∆ А1FC1 випливає
FC1 AC a + b 3
(2.28)
=
=
= = 3.
DB1 AD
a
1
Виражаємо катети трикутників через фізичні величини, якім вони
відповідають
DВ1 = ВВ1 – BD = ВВ1 – AA1= −∆l2 – ∆l1,
FC1 = CC1 – CF = CC1 – AA1= ∆l3 – ∆l1,
де AA1 = ∆l1, ВВ1 = –∆l2, CC1 = ∆l3.
З врахуванням (2.28) отримаємо рівняння сумісності переміщень
∆l3 − ∆l1
= 3,
− ∆l2 − ∆l1
остаточно маємо
2 ∆l1 + 3∆l2 + ∆l3 = 0 .
(2.29)
Відповідь: 2 ∆l1 + 3∆l2 + ∆l3 = 0 .
58
59.
3 НАПРУЖЕНО-ДЕФОРМОВАНИЙ СТАН В ТОЧЦІ3.1 Короткі теоретичні відомості
3.1.1 Поняття про напружений стан
Розглянемо напруження в будь-якій точці К тіла, що деформується
(рисунок 3.1, а). Величина повного напруження, яке діє на довільній
площадці, проведеній через точку К, залежить від орієнтації площадки.
Напруження, які діють на незліченній кількості по-різному орієнтованих
площадок, що проходять через розглядувану точку, характеризують
напружений стан у точці. Метод вивчення напруженого стану в точці
такий: вирізають елементарний паралелепіпед з ребрами dx, dy, dz
(рисунок 3.1,.б) і визначають напруження на його гранях. Враховуючи
малість розмірів паралелепіпеда і те, що всі його грані є площадками, які
проходять через точку К, то напруження по гранях паралелепіпеда можуть
розглядатися як напруження, що діють у точці К.
τzy
τzx
τxz
τxy
τyz
τyx
Рисунок 3.1
Повні напруження, які діють по кожній грані, розкладаємо на три
складові − на нормальне напруження σ і дотичні τ , як показано на
рисунку 3.1, б. На невидимих гранях елемента виникають відповідно такі
самі за величиною, але протилежного напрямку напруження. Перший
індекс у дотичного напруження вказує напрямок напруження, а другий −
напрямок нормалі до площини перерізу. Нормальні напруження будемо
позначати індексом осі, перпендикулярної до площадки.
Оскільки вирізаний елемент знаходиться в рівновазі, то склавши
суму моментів усіх сил відносно осі, яка геометрично збігається з
напруженням σх, маємо
∑ M σx = τ yz dx ⋅ dy ⋅ dz − τ zy dx ⋅ dy ⋅ dz = 0 ,
звідки отримуємо τ zx = τ xz . З рівнянь моментів відносно осей y і z маємо
59
60.
τ zx = τ x z , τ yx = τ x y .(3.1)
Отже, у двох взаємно перпендикулярних площадках дотичні
напруження перпендикулярні до спільного ребра і рівні за величиною. У
цьому полягає закон парності дотичних напружень.
Таким чином, напружений стан в будь-якій точці напруженого тіла,
яке деформується, визначається шістьма складовими σx , σy , σz , τxy , τxz, τzy,
які діють на трьох взаємно перпендикулярних площадках. Знаючи ці
складові, можна знайти напруження в будь-якій площадці, проведеній
через дану точку.
В курсі теорії пружності доводиться, що через незліченну кількість
площадок, які можна провести через довільну точку напруженого тіла,
завжди можна знайти такі три взаємно перпендикулярні площадки, на яких
дотичні напруження дорівнюють нулю. Такі площадки називаються
головними площадками, а діючі на них нормальні напруження −
головними напруженнями. Головні напруження позначають σ1 , σ2 , σ3, при
цьому повинна виконуватись умова σ1 > σ2 > σ3 (за алгебраїчною
величиною
Якщо). в будь-якій точці навантаженого тіла усі три напруження
відрізняються від нуля, то такий напружений стан називають об'ємним або
триосним. Якщо з трьох головних напружень одне дорівнює нулю, то
такий напружений стан називається плоским або двоосним. Напружений
стан, при якому два головних (з трьох) напруження дорівнюють нулю,
називається лінійним або одноосним. Прикладом лінійного напруженого
стану є звичайний центральний розтяг (стиск) стержня.
Аналіз напруженого стану в точці необхідний в першу чергу для
розрахунків на міцність в загальному випадку навантаження.
3.1.2 Плоский напружений стан
Оскільки при плоскому напруженому стані дві грані елементарного
паралелепіпеда вільні від напружень, то для спрощення міркувань
сумістимо ці грані з площиною рисунку (рисунок 3.2).
Якщо напруження σx , σy i τxн відомі, то можна визначити
напруження на довільній площадці, повернутій на кут α відносно
площадки, на якій діє напруження σ x (рисунок 3.2)
σ x1 = σ x cos 2 α + σ y sin 2 α − τ xy sin 2α ,
(3.2)
σ y1 = σ x sin 2 α + σ y cos 2 α + τ xy sin 2α ,
σ x −σ y
τ x1y1 =
sin 2α + τ xy cos 2α .
(3.3)
2
Із (3.2) і (3.3) випливає, що
60
(3.4)
61.
σ x + σ y = σ x 1 + σ y1 ,тобто сума нормальних напружень , що діють на двох взаємно
перпендикулярних площадках величина стала.
Правила знаків. Кут α
вважається додатним, якщо він
відкладається
проти
руху
τyx
годинникової
стрілки.
Розтягувальні
нормальні
τx1y1
τxy
напруження σ будемо вважати
додатними, а стискувальні −
τxy
від'ємними.
τy1x1
Дотичні
напруження
вважатимемо додатними τ >0, коли
τyx
вони будуть намагатись обертати
елемент відносно його центра за
Рисунок 3.2
годинниковою
стрілкою,
а
від’ємними – проти. Тоді закон парності дотичних напружень набуде
вигляду
τ yx = −τ xy .
(3.5)
3.1.3 Головні площадки і головні напруження
Знайдемо положення головних площадок. На головних площадках
дотичні напруження дорівнюють нулю, тому прирівнявши вираз (3.3) до
нуля, знайдемо
σ x −σ y
sin 2α 0 + τ xy cos 2α 0 = 0 ,
2
звідки
2τ xy
tg 2α 0 = −
,
(3.6)
σ x −σ y
або
tg α 0 = −
τ xy
σ1 − σ y
.
π
π
π
≤ α0 ≤
і α 0 + , які і
2
4
4
визначають положення двох головних площадок. Якщо σx > σy i τxн > 0 то
α0 буде додатним (рисунок 3.3).
Головні напруження можна визначити за формулами (3.2) і (3.4)
π
якщо замість α підставити α0 і α0 + , знайдені за формулою (3.6). Після
2
Формула (3.6) дає два значення кута −
61
62.
нескладних перетворень одержимоσx +σ y 1
2
σ max =
+
,
σ x − σ y 2 + 4τ xy
2
2
σ x +σ y 1
2
σ min =
−
σ x − σ y 2 + 4τ xy
.
2
2
(
)
(
(3.7)
)
Легко показати, що головні
напруження мають екстремальні
значення: одне з них є найбільшим
τyx
з усіх нормальних напружень, які
діють на численних площадках,
що проходять через дану точку, а
τxy
друге напруження − найменшим.
На площадках, нахилених
під кутом 45° до головних, діють
екстремальні дотичні напруження,
які рівні
σ
− σ min
τ max = max
. (3.8)
Рисунок 3.3
2
Нормальні напруження на цих площадках
σ0 =
σ max + σ min
2
=
σ x +σ y
2
.
(3.9)
3.1.4 Круг напружень
Залежності між складовими напружень та головними напруженнями
в даній точці можна виразити графічно за допомогою круга напружень, яке
також називається кругом Мора. Теоретичні передумови графічного
розв’язування ґрунтуються на залежностях (3.2 – 3.4), які являють собою
узагальнені параметричні рівняння кола в системі координат σ–τ. Роль
параметра відіграє кут α, що встановлює відповідність між точкою кола та
січною площадкою.
Круг Мора можна побудувати при відомих напруженнях на гранях
елемента (рис. 3.4). Нехай Dx – точка, положення якої в системі координат
σ–τ визначає напруження на площадці, перпендикулярні осі х, тоді
Dx(σх; τху), а Dy(σy; τyх). З врахуванням закону парності дотичних
напружень у вигляді (3.5) ці точки лежать на однаковій відстані від осі σ
по різні сторони. Центр круга Мора завжди лежить на осі σ, тому, для його
побудови, з’єднаємо точки Dx(σх; τху), а Dy(σy; τyх). Точка перетину відрізку
DxDy з віссю σ є центром круга Мора. Проводимо коло, що проходить
через точки Dx та Dy.
62
63.
у1τ
σx1
y
τх1у1
A(σx1;τх1у1)
τх1у1
τxу
α
M(σy;τxу)
x1
σx
Dx(σx;τxу)
τxу
α
σ2
α0
σy1
σy
0
x
О σх1
σ1
σx
σ
σ1
σ2
τyх
Dy(σy;τyх)
τу1х1
B(σy1;τу1х1)
τух
τу1х1
σу
τух<0
σу1
у
у
у1
σу>0
σу1
τу1х1
х1
τху
τх1у1
σх>0 х
σх
τх1у1
σх1
τху>0
σу
σх1 α
τу1х1
τух
σу1
Рисунок 3.4
63
х
64.
Полюс круга Мора визначає початкове положення елемента α = 0.Полюс при прийнятих позначеннях відповідає точці з координатами
М(σy ;τху). Проведемо промені з точки М в точки Dx та Dy. Площадки,
перпендикулярні цим променям (заштриховані), утворюють початкове
положення елемента.
Визначення головних напружень за допомогою круга Мора.
Головні напруження набувають екстремальних значень, тобто одне з
них алгебраїчно найбільше, інше – найменше. Напружений стан в точці
визначають тільки точки круга Мора, тому найбільше нормальне
напруження відповідає крайній правій точці (σ1), а найменше – крайній
лівій (σ2 або σ3). Це – діаметрально протилежні точки, що лежать на осі σ.
Положення першої головної площадки визначається кутом, утвореним
променем, що проходить через точку (σ1) та віссю σ. Аналогічно
визначається положення другої головної площадки, яка завжди повернута
на 900 відносно першої.
Визначення напружень при повороті площадки за допомогою круга
Мора.
Проведемо через полюс М пряму, що утворює кут α з віссю σ. Кут α
вважається додатним, якщо він відкладається проти руху годинникової
стрілки. Ця пряма перетинає круг в деякій точці А. Координати точки А
(σх1; τх1у1) визначають напруження на площадці при повороті на кут α до
заданої, на якій діють напруження Dx(σх; τху).
Проведемо через полюс М пряму, що перпендикулярна прямій, яка
утворює кут α з віссю σ. Перетин прямої з колом дасть координати точки
В (σу1; τу1х1), які визначають напруження на площадці при повороті на кут
α до заданої, на якій діють напруження Dу(σу; τух).
3.1.5 Узагальнений закон Гука
Досліджуючи деформації і розглядаючи питання міцності при
об'ємному та плоскому напружених станах, будемо в відповідності з основними гіпотезами і припущеннями вважати, що матеріал поводиться
згідно з законом Гука, а деформації малі.
Зв'язок між відносними деформаціями і напруженнями при
об'ємному напруженому стані має вигляд
τ xy
1
σ x − µ σ y + σz , γ xy =
,
E
G
τ yz
1
εy =
σ y − µ(σ x + σ z ) , γ yz =
,
E
G
τ
1
εz =
σ z − µ σ x + σ y , γ zx = zx ,
E
G
εx =
[
(
)]
(
]
)]
[
[
64
(3.10)
65.
де µ − коефіцієнт Пуассона, E − модуль Юнга, G − модуль зсуву.Співвідношення (3.10) є аналітичним виразом узагальненого закону
Гука для ізотропного тіла.
В головних напруженнях формули (3.10) мають вигляд
1
[σ 1 − µ (σ 2 + σ 3 )],
E
1
ε 2 = [σ 2 − µ (σ 1 + σ 3 )],
E
1
ε 3 = [σ 3 − µ (σ 1 + σ 2 )].
E
ε1 =
(3.11)
Відносна зміна об’єму елемента з точністю до величин другого
порядку малості
εV = ε1 + ε 2 + ε 3 =
1− 2µ
[σ 1 + σ 2 + σ 3 ] .
E
(3.12)
3.1.6 Потенціальна енергія деформації
Потенціальною енергією деформації називається енергія, яка
накопичується в тілі при його пружній деформації. Коли під дією
зовнішнього статичного навантаження тіло деформується, точки
прикладання зовнішніх сил переміщуються і потенціальна енергія
положення вантажу зменшується на величину, яка чисельно дорівнює
роботі, виконаній зовнішніми силами. Енергія, витрачена зовнішніми
силами, не зникає, а перетворюється, в основному, в потенціальну енергію
деформації тіла. Решта, незначна частина розсіюється, головним чином, в
вигляді тепла за рахунок різних процесів, що проходять в матеріалі при
його деформації
Величину . потенціальної енергії деформації, що припадає на
одиницю об'єму тіла, називають питомою потенціальною енергією
деформації і визначають за формулою
u=
Маючи на увазі, що ε =
P∆l σε
=
.
2 Al
2
(3.13)
σ
, одержимо для питомої потенціальної
Е
енергії деформації вираз
σ2
u=
.
2E
65
(3.14)
66.
Для загального випадку визначення питомої потенціальної енергіїдеформації при об'ємному напруженому стані, якщо задані головні
напруження формула має вигляд
u=
[
]
1 2
σ 1 + σ 22 + σ 32 − 2µ (σ 1σ 2 + σ 2 σ 3 + σ 3 σ 1 ) .
2E
(3.15)
При деформації елемента змінюється, як його об'єм, так і форма (із
куба він перетворюється на паралелограм). В зв'язку з цим можна вважати,
що повна питома потенціальна енергія деформації
u = uV + u Ф .
(3.16)
де uV − питома потенціальна енергія зміни об'єму, тобто енергія, яка
накопичується за рахунок зміни об'єму;
uф − питома потенціальна енергія формозміни, тобто енергія, яка
накопичується внаслідок зміни форми елемента.
Безпосередньо визначити uф важко, тому спочатку визначимо uV.
uV =
1 − 2µ
(σ1 + σ 2 + σ 3 )2 .
6E
(3.17)
Тепер, згідно з формулою (3.16),
uф = u − uv .
Підставляючи сюди значення u і uv із (3.15) і (3.17), після елементарних
перетворень отримаємо, що
(
)
1+ µ 2
σ 1 + σ 22 + σ 32 − σ 1σ 2 − σ 2σ 3 − σ 3σ 1 =
3E
1+ µ
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 .
=
(3.18)
6E
Це і є шуканий вираз для питомої потенціальної енергії формозміни.
В теорії пластичності часто використовують величину, від якої залежить
перехід матеріалу в стан текучості, це – інтенсивність нормальних
напружень, яка збігається з еквівалентним напруженням за четвертою
теорією міцності
1
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 .
σi =
(3.19)
2
1+ µ 2
тоді u Ф =
σi .
3E
uФ =
[
]
66
67.
3.2 Завдання до розрахунково-графічної роботиЗадача 3. Дослідження плоского напружено-деформованого стану
в точці
Для заданого прямокутного елемента, що знаходиться в умовах
плоского напруженого стану та навантаженого згідно з схемою (рис. 3.5 –
3.7), необхідно:
а) обчислити величину і напрямок головних напружень;
б) показати положення головних площин з головними напруженнями;
в) обчислити величину і напрям найбільших (найменших) дотичних
напружень і відповідних їм нормальних напружень, показати їх на
рисунку;
г) обчислити і показати на рисунку напруги на гранях елемента при
послідовному повороті заданого елемента на 300 та 600 в напрямі кута
γ;
д) обчислити
коефіцієнт запасу міцності в точці, використовуючи IV
(енергетичну) теорію міцності;
е) обчислити величини питомої потенціальної енергії зміни форми та
об’єму елемента і повну питому потенціальну енергію деформації;
ж) обчислити головні видовження і відносну зміну об’єму елемента;
и) обчислити відносне видовження ребра АВ елемента, повернутого на
кут γ.
На окремому аркуші А4 побудувати круг Мора та графічно
перевірити розв’язок пунктів а), б), в), г).
Таблиця 3.1
Варіант
0
1
2
3
4
5
6
7
8
9
/σх/,
МПа
80
50
20
20
30
40
50
60
60
70
/σу/,
МПа
20
50
40
60
40
60
30
40
30
20
/τ/,
МПа
40
30
50
50
60
80
50
20
40
30
γ °,
60
-30
80
45
30
-60
120
90
20
50
Матеріал
(сталь)
30
45
20Г
40Х
30ХГСА
50ХН
10
30ХН3А
12ХН3А
35ХМ
В варіантах схем, де деякі вектори напружень відсутні, вважати їх
рівними нулю незалежно від приведених в таблиці значень.
67
68.
0100
τyx
τxy
σy
B
x
σy
A
τyx
σy
B
σx
γ
τyx
τxy A
τyx
τxy
τxy
γ
σy
02
03
σy
τyx
τxy
B
σx
σy
A
τyx
σy
B
σx
σx
γ
τxy A
τyx
τxy
04
τxy
B
τxy
τxy
A
τyx
σy
Рисунок 3.5
68
γ
σx
σy
B
γ
A
τxy
05
σy
τyx
τyx
τyx
γ
τxy
τyx
69.
0706
σy
B
τxy A
τyx
τyx
τyx
τxy
τxy
γ
B
σx
σx
γ
A
τyx
σy
τxy
09
08
τху
B
σx
σy
τyx
γ
σx
τyx A
τху
τxy
B
σx
τyx A
τху
τyx
γ
σx
σy
11
τyx
τxy
τyx
B
σx
σx
γ
A
σy
B
10
σy
τyx
σx
τху
τxy
σx
γ
A
τyx
Рисунок 3.6
69
τxy
70.
12σy
τyx
B
τxy A
τyx
13
τxy
τxy
γ
σy
τyx
B
σx
A
14
σy
σx
τyx
B
τxy A
τyx
τyx
τxy
τxy
σx
τyx
B
γ
15
σx
γ
A
τyx
σy
16
τyx
B
τxy A
τyx
σy
Рисунок 3.7
70
τxy
17
σy
τxy
τxy
σy
B
σy
σy
τxy A
τyx
γ
τyx
σy
σy
σx
γ
γ
σy
τxy
71.
Приклад. Дослідити плоский напруженийстан прямокутного елемента в точці згідно з
приведеним в задачі 3 порядком виконання.
Елемент
навантажений
згідно
схеми,
приведеної на рисунку 3.8.
/σх/= 100 МПа, /σу/= 20 МПа, /τ/= 80 МПа,
γ°= 450, матеріал – сталь 20.
Розв’язування
σy
σx
τxy A
τyx
τyx
B
γ
τxy
σx
σy
Вибір знаків напружень (користуємось
Рисунок 3.8
правилом знаків – див рис. 3.2, 3.4)
σх = +100 МПа, σу = –20 МПа, τух = 80 МПа, τху = –80 МПа.
Визначення головних (найбільших та найменших напружень)(3.7)
σ x +σ y 1
2
σ max/ min =
±
σ x − σ y 2 + 4τ xy
=
2
2
100 + ( −20 ) 1
(100 − ( −20 ))2 + 4( −80 )2 = 40 ± 100 (МПа ),
=
±
2
2
Звідки знаходимо, з урахуванням умови σ1 > σ2 > σ3
σ max = σ 1 = 140 МПа,
σ min = σ 3 = −60 МПа,
σ 2 = 0 МПа.
Визначення положень головних площадок
τ xy
− 80
tg α 0 = −
=−
= 0,5 ,
σ1 − σ y
140 − ( −20 )
звідки α 0 = 26033/ (кут нахилу площадки, на якій діє σ 1 до площадки, на
якій діє σ x ).
Положення другої головної площадки α 0 / = α 0 + 900 = 26033/ + 900 =
116033/.
Визначення максимальних та мінімальних дотичних напружень (3.8)
(3.9)
σ
− σ min 140 − ( −60 )
τ max = max
=
= 100 МПа,
2
2
τ min = −τ max = -100 МПа.
Максимальні дотичні напруження діють на площадках, нахилених
під кутом 45° до головних, тому їх положення визначимо кутом β, який
знайдемо за формулою
β = α 0 + 450 = 26033/ + 450 = 71033/ ;
β/ = β + 900 = 71033/ + 900 = 161033/ .
β – кут нахилу площадки, на якій діє τ max до площадки, на якій діє σ x ,
β/ – кут нахилу площадки, на якій діє τ min до площадки, на якій діє σ x .
(
)
71
72.
Нормальні напруження на цих площадках, де діють τ max (τ min ) рівніміж собою, а їхня величина дорівнює гідростатичному тиску в точці
σ
+ σ min 140 + ( −60 )
σ 0 = max
=
= 40 МПа.
2
2
Обчислення напружень на гранях елемента при послідовному
повороті заданого елемента на 300 та 600 в напрямі кута γ (3.2 – 3.4)
α1 = 300
σ x1 = σ x cos 2 α1 + σ y sin 2 α1 − τ xy sin 2α1 =
(
)
= 100 cos 2 30 0 + ( −20 ) sin 2 30 0 + ( −80 ) sin 2 ⋅ 30 0 = 139,3 МПа,
σ y1 = σ x sin 2 α1 + σ y cos 2 α1 + τ xy sin 2α1 =
(
)
= 100 sin 2 30 0 + ( −20 ) cos 2 30 0 + ( −80 ) sin 2 ⋅ 30 0 = -59,3 МПа,
σ x −σ y
τ x1y1 =
sin 2α1 + τ xy cos 2α1 =
2
100 − ( −20 )
sin 2 ⋅ 30 0 + ( −80 ) cos 2 ⋅ 30 0 = 11,96 МПа,
=
2
τ x1y1 = −τ y1x1 = −11,96 МПа .
(
)
(
)
α2 = 600
σ x 2 = σ x cos 2 α 2 + σ y sin 2 α 2 − τ xy sin 2α 2 =
(
)
= 100 cos 2 60 0 + ( −20 ) sin 2 60 0 − ( −80 ) sin 2 ⋅ 60 0 = 79,28 МПа,
σ y 2 = σ x sin 2 α 2 + σ y cos 2 α 2 + τ xy sin 2α 2 =
(
)
= 100 sin 2 60 0 + ( −20 ) cos 2 60 0 + ( −80 ) sin 2 ⋅ 60 0 = 0,72 МПа,
σ x −σ y
τ x 2 y2 =
sin 2α 2 + τ xy cos 2α 2 =
2
100 − ( −20 )
=
sin 2 ⋅ 60 0 + ( −80 ) cos 2 ⋅ 60 0 = 91,96 МПа,
2
τ x 2 y2 = −τ y2 x 2 = −91,96 МПа .
Перевірка
σ x + σ y = σ 1 + σ 2 = σ x1 + σ y1 = σ x 2 + σ y2 ,
(
)
(
)
100 + ( −20 ) = 140 + ( −60 ) = 139,3 + ( −59,3 ) = 79,28 + 0,72 = 80 ,
розрахунки нормальних напружень виконані вірно.
Коефіцієнт запасу міцності в точці за IV (енергетичною) теорію
міцності.
Інтенсивність нормальних напружень (еквівалентне напруження за
четвертою теорією міцності) (3.19)
1
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 =
σi =
2
72
73.
1(140 − 0)2 + (0 − ( −60 ))2 + (( −60 ) − 140)2 = 177,76 МПа.
2
Коефіцієнт запасу
σ
250
n= т =
= 1,41.
σ i 177,76
де σт = 250 МПа − границя текучості сталі 20 (див. додаток Ж),
Обчислення величин питомої потенціальної енергії зміни форми та
об’єму елемента і повна питома потенціальну енергія деформації.
1+ µ
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2 = 1 + µ σ i2 =
uФ =
6E
3E
1 + 0,25
-2
3
2
177
.
76
=
6,583⋅10
(
МПа
)
=
65830
(
Дж
/
м
).
3 ⋅ 2 ⋅105
1− 2µ
(σ 1 + σ 2 + σ 3 )2 =
uV =
6E
1 − 2 ⋅ 0,25
(140 + ( −60 ))2 =2,667⋅10-3 (МПа) = 2667 (Дж/м3).
=
5
6 ⋅ 2 ⋅10
u = uV + u Ф = 65830 + 2667 = 68497 (Дж/м3),
де Е = 2⋅1011 Па = 2⋅105 МПа – модуль пружності І роду,
µ = 0,25 – коефіцієнт Пуассона (для сталі).
Головні видовження (3.11)
1
1
-4
(
)
ε1 = [σ 1 − µ (σ 2 + σ 3 )] =
[
140
−
0
,
25
0
+
(
−
60
)
]
=
7,75⋅10
;
E
2 ⋅105
1
1
ε 2 = [σ 2 − µ (σ 1 + σ 3 )] =
[0 − 0,25(140 + ( −60))] = –1⋅10-4;
5
E
2 ⋅10
1
1
ε 3 = [σ 3 − µ (σ 1 + σ 2 )] =
[− 60 − 0,25(140 + 0)]= –4,75⋅10-4.
5
E
2 ⋅10
Відносна зміна об’єму елемента з точністю до величин другого
порядку малості (3.12)
εV = ε1 + ε 2 + ε 3 = 7,75 ⋅10 −4 + ( −1 ⋅10 −4 ) + ( −4,75 ⋅10 −4 ) = 2,75⋅10-4.
Обчислення відносного видовження ребра АВ елемента, повернутого
на кут γ. Знаходимо нормальні напруження, що діють на площадках,
повернутих на кут γ ( σ γ ) та кут γ + 900 ( σ γ +900 ).
=
[
]
γ = 450
σ γ = σ x cos 2 γ + σ y sin 2 γ − τ xy sin 2γ =
(
)
= 100 cos 2 45 0 + ( −20 ) sin 2 45 0 − ( −80 ) sin 2 ⋅ 45 0 = 120 МПа,
σ γ +900 = σ x sin 2 γ + σ y cos 2 γ + τ xy sin 2γ =
(
)
= 100 sin 2 45 0 + ( −20 ) cos 2 45 0 + ( −80 ) sin 2 ⋅ 45 0 = –40 МПа.
73
74.
Відносне видовження ребра АВ визначаємо за узагальненим закономГука (3.10) при плоскому напруженому стані
1
1
ε γ = σ γ − µσ γ +900 =
[120 − 0,25(− 40)] = 6,5⋅10-4.
5
E
2 ⋅10
Будуємо круг Мора (користуйтесь прикладними програмами для
побудови круга Мора, наприклад, КОМПАС 5.11) та показуємо на рисунку
всі величини, що розраховуються графічно (методика побудови див. п.
3.1.4), а також положення площадок і відповідних їм напружень (рис. 3.9).
[
]
Ó
τ , ÌÏà
σy
τ yx
σo
σ x2
τ ma x
τ x2 y2
100
Dy(σ y,τ yx)
80
σ y1
σ3
60
σ x1
40
τ x1 y1
σ1
20
-6 0
B1(σ y1 ,τ y1 x1 )
-4 0 -2 0
20
-2 0
-4 0
40
60
σ , ÌÏ à
80 100 120 140
α1
-60
α0
β
α 'o
A1(σ x1 ,τ x1 y1 )
X1
τ xy
β'
τ y1 x1
A2(σ x2 ,τ x2 y2 )
α2
τ m in = - 1 0 0
τ xy= - 8 0
τ y1 x1 = - 1 1 , 9 6
τ m ax= 1 0 0
τ y x =8 0
τ x1 y1 =11,96
Ó1
M(σ y,τ xy)
-8 0
B2(σ y2 ,τ y2 x2 )
- 10 0
Dõ(σ õ,τ õy)
σx
X
σ o= 4 0
σ y= - 2 0
σ õ=100
σ y1 = - 5 9 , 3
σ x1 =139,3
σ 3= - 6 0
σ 1= 1 4 0
Рисунок 3.9
74
τ min
σo
τ y2 x2
σ y2
75.
4 ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ ПЛОСКИХ ПЕРЕРІЗІВ4.1 Короткі теоретичні відомості
Опір стержня різним видам деформації залежить не тільки від його
матеріалу і площі поперечного перерізу, а і від форми поперечного
перерізу, і його розміщення по відношенню до діючих навантажень. Досі
вивчалися деформації, у яких напруження залежали тільки від площі
поперечного перерізу. Для вивчення деформацій згину і кручення потрібно
знати й інші, більш складні геометричні характеристики плоских перерізів.
4.1.1 Статичний момент площі. Центр ваги перерізу
Статичним моментом Sz або Sy площі перерізу відносно осі z або y,
які лежать у площині перерізу, називаються інтеграли виду
S z = ∫ y ⋅ dА,
S y = ∫ z ⋅ dА ,
А
А
n
S y = ∑ Аi z i ,
(4.1)
де z та y − відстані від центра елементарної площадки до осей Oz та Oy .
У більшості практичних (інженерних) задач можна інтегрування
замінити сумою, розділивши переріз на частини, площі і положення
центрів ваги яких відомі, наприклад, переріз на рис. 4.2 можна розділити
на окремі прямокутники. Тоді замість (4.1) можна записати
n
S z = ∑ Аi y i ,
i =1
(4.2)
i =1
y
yc
yc
yi
де n − кількість окремих частин перерізу,
Аi − площа частини перерізу,
zi , yi − відстані від центра ваги цієї площі до осей Oz та Oy.
Положення центра ваги перерізу C відносно будь-яких осей z та y
(рисунки 4.1 і 4.2) визначається за формулами
Рисунок 4.1
Рисунок 4.2
75
76.
zC =Sy
А
,
yC =
Sz
,
А
(4.3)
де А− площа перерізу,
Sz та Sy − статичні моменти площі перерізу відносно осей z та y.
Статичний момент площі може бути величиною додатною,
від’ємною і дорівнювати нулю. Статичний момент відносно осі, яка
проходить через центр ваги фігури (центральної осі) дорівнює нулю.
4.1.2 Моменти інерції перерізу
Осьовими моментами інерції Iz та Iy перерізу відносно будь-яких
осей z та y, що лежать у площині перерізу (рисунок 4.1) називають
інтеграли виду
I z = ∫ y 2 dА ,
I y = ∫ z 2 dА ,
А
А
(4.4)
де y та z − відстані від елементарної площадки dА до осей Oz та Oy.
Відцентровим моментом інерції Izy перерізу відносно осей Oz та Oy,
які лежать у площині перерізу, називається інтеграл виду
I zy = ∫ zy ⋅ dА .
(4.5)
А
Інтеграл від добутків елементарних площадок на квадрати їх
відстаней до даної точки (полюса) O (рисунок 4.1) називається полярним
моментом інерції
I p = ∫ ρ 2 dА .
(4.6)
А
Осьові і полярний моменти інерції завжди додатні, відцентровий
момент інерції може бути додатним, від’ємним і рівним нулю.
Якщо полюс О збігається з початком координатних осей z, y, то
Ip=Iz+Iy.
(4.7)
Із (4.7) випливає, що при повороті осей координат сума осьових
моментів інерції залишається незмінною.
За формулами (4.4 − 4.6) легко підрахувати моменти інерції для
перерізів, які часто зустрічаються на практиці. Наприклад, для
прямокутника (рисунок 4.3)
76
77.
b ⋅ h3;
Iz =
12
h ⋅ b3
.
Iy =
12
(4.8)
Для круга
Iz = I y =
π ⋅d4
64
.
(4.9)
для трикутника відносно центральної осі паралельної основі
Iz =
b ⋅ h3
.
36
(4.10)
h
h
Полярний момент інерції круга відносно полюса, розміщеного в
центрі ваги
π ⋅ d4
Ip =
.
(4.11)
32
Рисунок 4.3
4.1.3 Формули переходу до паралельних або повернутих осей
Нехай система координат zCyC проходить через центр ваги C перерізу
(рисунок 4.4), а друга система yz, що має початок у точці O, паралельна їй.
Відстані між осями цих систем позначимо через a і b. Якщо відомі
моменти інерції площі А відносно центральних осей zC і yC − I zc , I yc i I zc yc ,
то відносно осей z , y, паралельних центральним осям (рисунок 4.4)
моменти інерції знаходять за формулами
I z = I zc + a 2 А ,
I y = I yc + b 2 А ,
I zy = I zc yc + abА .
77
(4.12)
78.
аРисунок 4.5
Рисунок 4.4
При повороті координатних осей на кут α (рисунок 4.5) залежність
між моментами інерції така:
I z = I z cos 2 α + I y sin 2 α − I zy sin 2α ,
1
I y = I z sin 2 α + I y cos 2 α + I zy sin 2α .
(4.13)
1
Iz y =
Iz − I y
2
1 1
sin 2α + I zy cos 2α .
(4.14)
Кут α>0 при повороті осей проти стрілки годинника.
Момент інерції складної фігури (рисунок 4.2) дорівнює сумі
моментів інерції простих фігур
n
I z = ∑ I zi ;
i =1
n
I y = ∑ I yi ;
i =1
n
I zy = ∑ I zi yi .
i =1
(4.15)
де n − кількість окремих частин перерізу,
I zi , I yi , I zi yi − момент інерції і-тої частини відносно довільно вибраних
осей z, y. Тобто, для кожної частини вони взяті відносно одних і тих же
осей.
4.1.4 Головні осі інерції та головні моменти інерції перерізу
Головними називають осі, відносно яких відцентровий момент
інерції перерізу дорівнює нулю. Найбільший практичний інтерес мають
головні центральні осі, на відміну від інших позначимо їх через u i v
(рисунок 4.6). В розрахункових формулах їх часто позначають також через
y i z. Для визначення положення головних центральних осей u та v
використаємо формулу (4.14) переходу до повернутих осей (у даному
випадку до головних осей uv), підпорядкувавши її умові Iuv = 0. Тоді для
78
79.
знаходження кута α0 (рисунок 4.6), щовизначає положення головних осей
відносно
будь-яких
допоміжних
центральних осей zy, отримаємо
tg2α 0 =
2I zy
I y − Iz
.
(4.16)
Формула дає два значення кута α0,
π
що відрізняються на
і визначають
Рисунок 4.6
2
положення
двох
взаємно
перпендикулярних головних осей інерції.
Моменти інерції відносно головних осей називаються головними
моментами інерції. Головні моменти інерції мають екстремальні значення,
тобто один має найбільше, а другий найменше значення із всіх отриманих
при повороті осей координат. Сума осьових моментів інерції при повороті
осей координат величина стала
Iz + I y = Iz + I y = Iu + Iv.
1
1
(4.17)
Головні моменти інерції позначимо Iu , Iv або Imax , Imin . Їх можна
підрахувати за формулами (4.13) з врахуванням того, що α=α0, або
Iz − Iy
1
2
( I z − I y )2 + 4 ⋅ I zy
,
2
2
Iz − I y 1
2
I min =
−
( I z − I y )2 + 4 ⋅ I zy
.
2
2
I max =
+
(4.18)
Із залежності (4.17) випливає, що при повороті допоміжних осей zy
до збігу з головними осями uv більший з моментів інерції відносно
допоміжних осей повинен збільшитися і досягти величини Imax , тоді як
менший повинен зменшитися на ту саму величину й досягти Imin . Отже
віссю максимального моменту завжди буде вісь, суміжна з тією
допоміжною віссю (z або y), відносно якої момент інерції більший. Якщо,
наприклад, Iz > Iy , то вісь u, що з віссю z становить гострий кут (рисунок
4.5), буде віссю Imax . У випадку, коли Jzс < Jус Ju = Jmin, Jv = Jmax та навпаки
Ju = Jmax, Jv =Jmin, коли Jzс > Jус .
Потрібно відмітити, що отримані за формулою (4.16) значення α0
потрібно відкладати проти стрілки годинника, якщо вони додатні, і за
стрілкою годинника, якщо вони від’ємні.
Якщо відомі значення головних моментів інерції Imax , Imin та осьових
79
80.
I z c ,I y c , то відцентровий момент інерції відносно осей хс та ус можнавизначити за одною з нижченаведених формул:
J zc yc = ± J zc J yc − J max J min ;
J zc yc = ±
(4.19)
(J max − J min )2 − (J zc − J yc )2 ;
(4.20)
(
)(
)
J z y = ± ( J max − J z )(J max − J y ) .
J zc yc = ± J zc − J min J yc − J min ;
c c
c
(4.21)
(4.22)
c
Знак в формулах (4.19) – (4.22) вибирається в залежності від положення
перерізу (наприклад, для нерівнобокого кутика він показаний на рис. 4.7.
Для схем а, г – J zc yc > 0; б, в – J zc yc < 0.
4.1.5 Радіуси інерції. Моменти опору
Радіусом
інерції
перерізу
називають величину виду
Iy
I
iz = z , i y =
.
(4.23)
А
А
Головні радіуси інерції перерізу
отримаємо, якщо у формулу (4.23)
підставимо головні моменти інерції
I
I
i max = max , i min = min . (4.24)
А
А
Осьовим
моментом
опору
називається частка від ділення
головного моменту інерції на відстань
від осі до найбільш віддаленої від неї
точки перерізу
Iy
I
Wz = z ,
Wy =
. (4.25)
y max
z max
а
Jmin
б
Jmin
в
г
Jmin
Jmin
Рисунок 4.7
де Iz , Iy − головні моменти інерції.
Чaстка від ділення полярного моменту інерції на відстань від центру
до найбільш віддаленої точки перерізу називається полярним моментом
опору
I
Wp = z .
(4.26)
ρ max
80
81.
Для прямокутникаДля круга W z = W y =
b ⋅ h2
Wz =
,
6
h ⋅ b2
Wy =
.
6
π ⋅d3
π ⋅d3
32
Wp =
,
16
.
(4.27)
(4.28)
4.2 Завдання до розрахунково-графічної роботи
Задача 4. Обчислення геометричних характеристик складного
перерізу*
Для заданого поперечного перерізу бруса, що складений із двотавру
(швелера), кутика нерівнобокого та штаби (рис. 4.8, 4.9) необхідно:
а) визначити положення центра ваги;
б) обчислити величини осьових та відцентрових моментів інерції перерізу
в системі координат центральних горизонтальної та вертикальної осей;
в) визначити напрямок головних центральних осей;
г) обчислити величини головних центральних моментів інерції;
д) обчислити величини моментів опору перерізу;
е) накреслити переріз в масштабі (1:1 або 1:2), нанести всі розрахункові
розміри та показати центральні, головні та допоміжні осі.
Дані для розрахунку взяти із таблиці 4.1.
Таблиця 4.1
Розміри елементів перерізу
Номер профілю
Кутик
Штаба
двотавра
нерівнобокий
Варіант
(ГОСТ 8239-72)
(ГОСТ 8510-86)
товщина, ширина,
або швелера
мм
мм
Товщина
Номер
(ГОСТ 8240-72)
полки
0
10
6,3/4,0
5
4
40
1
12
7/4,5
5
6
60
2
14
7,5/5
8
8
100
3
16
8/5
5
10
80
4
18
9/5,6
8
12
100
5
20
10/6,3
8
14
40
6
22
11/7
8
16
160
7
24
12,5/8
10
18
60
8
27
14/9
10
20
180
9
30
16/10
10
25
200
* Користуйтесь прикладними програмами ПЕОМ для виконання завдання
(додаток В)
81
82.
0004
01
05
02
06
03
07
Рисунок 4.8
82
83.
0812
09
13
10
14
11
15
Рисунок 4.9
83
84.
Приклад. Для заданого поперечного перерізу бруса,що складений із двотавра №18а, кутика нерівнобокого
№11х7 (t = 8 мм) та штаби 10х100 мм визначити положення
центра ваги; обчислити величини осьових та відцентрових
моментів інерції перерізу в системі координат центральних
горизонтальної та вертикальної осей; визначити напрямок
головних центральних осей; обчислити величини головних
центральних моментів інерції; обчислити величини
моментів опору перерізу; накреслити переріз в масштабі
(1:1 або 1:2), нанести всі розрахункові розміри та показати
центральні, головні та допоміжні осі.
Рисунок 4.10
Розв’язування
Вибір та обґрунтування вихідний даних
Креслимо переріз в масштабі 1:1 або 1:2 – рис.4.11, користуючись
розмірами, наведеними в таблицях сортаменту (додаток Д). Вибираємо
довільно допоміжні осі х та у (одна із осей паралельна осі двотавра). Для
кожної складової складного перерізу позначаємо центральні осі, що
паралельні вибраним осям.
Вказівка. На кресленні проставляються всі розміри, що
використовуються в розрахунках поруч із їхніми буквеними позначеннями.
Рекомендується для зручності розрахунку розміри проставляти у
сантиметрах.
Із таблиць сортаменту (додаток Д) виписуємо необхідні для
розрахунків геометричні характеристики двотавра (індекс 1) та кутика
(індекс 2) відповідно до вибраних центральних осей.
Для двотавра №18а
Площа А1 = 25,4 см2; центральні осьові моменти інерції Jу1 =
= 114,0 см4; Jz1 = 1430 см4; відцентровий момент інерції Jz1y1 = 0. Центр
ваги перерізу С1 лежить на осі симетрії посередині стояка.
Для кутика нерівнобічного № 11х7 (t = 8 мм)
Площа А2 = 13,9 см2; центральні осьові моменти інерції Jy2 =
= 172,0 см4; Jz2 = 54,6 см4; відцентровий момент інерції Jz2y2 = +55,9 см4
(знак при Jz2y2 вибираємо за рис. 4.7).; положення центру ваги перерізу С2
визначається величинами уc2 = 1,64 см, zc2 = 3,61 см.
Для штаби 10х100 мм
Позначимо сторони штаби b = 1 см, h = 10 см.
Площа А3 = h⋅b = 1⋅10 = 10 см2;
центральні осьові моменти інерції прямокутного перерізу (4.8)
hb 3 10 ⋅13
Jy3 =
=
= 0,83 см4;
12
12
3
bh
1 ⋅103
Jz3 =
=
= 83,33 см4;
12
12
84
85.
відцентровий момент інерції Jz3y3 = 0 см4;y2 yñ y1
z1
à2=-0,4
zñ
a0=13Å38'
U
z2
Ñ2
Ñ3
y3=5ñì
Umax=7,
673
z3
z
z3=0,5
yñ2=1,64
yñ=13,16ñì
Ñ
â1=5,84ñì
Ñ1
â2=-4,8ñì
â3=-8,16ñì
y1=19,0ñì
Vmax=16
,113ñì
z1=7,0ñì
z2=4,61ñì
à3=-4,51ñì
à1=1,99ñì
V
y2=8,36ñì
y y3
zc2=3,61
zñ=5,01ñì
Рисунок 4.11
Центр ваги перерізу С3 лежить на перетині осей симетрії (або
діагоналей) перерізу.
Визначення центру ваги перерізу (формули 4.2, 4.3)
A z + A2 z 2 + A3 z 3 25.4 ⋅ 7 + 13.9 ⋅ 4.61 + 10 ⋅ 0.5
=
= 5,01 (см);
zc = 1 1
A1 + A2 + A3
25.4 + 13.9 + 10
85
86.
A1 y1 + A2 y 2 + A3 y 3 25.4 ⋅19.0 + 13.9 ⋅ 8.36 + 10 ⋅ 5.0=
= 13,16 (см).
A1 + A2 + A3
25.4 + 13.9 + 10
На рис. 4.11 вказуємо центральні осі zс – yс та позначаємо центр ваги С
складного перерізу.
Визначення моментів інерції перерізу
Знаходимо координати центрів ваги С1(a1; b1), С2(a2; b2) та С3 (a3; b3)
в системі центральних осей zс – yс.
a1 = z1 – zc = 7,0 – 5,01 = 1,99 (см),
a2 = z2 – zc = 4,61 – 5,01 = -0,4(см),
a2 = z2 – zc = 0,5 – 5,01 = -4,51 (см),
b1 = y1 – yc = 19,0 – 13,16 = 5,84 (см),
b2 = y2 – yc = 8,36 – 13,16 = -4,8(см),
b3 = y3 – yc = 5,0 – 13,16 = -8,16 (см).
Центральні осьові моменти інерції перерізу (формули 4.12)
Jzс = Jz1 + b12 ⋅А1+ Jz2 + b22 ⋅А2 + Jz3 + b32 ⋅А3 =
= 1430 + 5,842⋅25,4 + 54,6 + (-4,8)2⋅13,9 + 83,33 + (-8,16)2⋅10 = 3420,3 (см4);
Jус = Jу1 + a12 ⋅А1+ Jу2 + a22 ⋅А2 + Jy3 + a32 ⋅А3 =
= 114 + 1,992⋅25,4 + 172 + (-0,4)2⋅13,9 + 0,83 + (-4,51)2⋅10 = 593,0 (см4).
Відцентровий момент інерції складного перерізу
Jzсус = Jz1у1 + a1b1⋅А1 + Jz2у2 + a2b2 ⋅А2 + Jz3у3 + a3b3 ⋅А2 =
= 0 + 1,99⋅5,84⋅24,0 + 55,9 + (-0,4)(-4,8)⋅13,9 + 0 + (-4,51)(-8,16)⋅10 =
= 729,52 (см4).
Визначення напрямку головних центральних осей та головних моментів
інерції перерізу
Кут нахилу головних центральних осей інерції перерізу (формула 4.16)
2 J zcyc
2 ⋅ 729.5
=
= -0,4856,
tg 2α 0 =
J yc − J zc 593 − 3420.3
yc =
звідки знаходимо α0 = -130 38/.
Головні центральні моменти інерції перерізу (формула 4.18)
J u /v =
=
2
(J zc − J yc )2 + 4J zcyc
J zc + J yc ±
3420.3 + 593.0 ±
2
=
(3420.3 − 593.0)2 + 4 ⋅ 729.52
2
= 2006,7 ± 1590,8 (см4).
Звідки знаходимо Ju= Jmax = 3597,4 см4; Jv = Jmin = 415,9 см4.
Ju = Jmax, Jv =Jmin, оскільки Jzс > Jус .
(У випадку, коли Jzс < Jус Ju = Jmin, Jv = Jmax ).
Перевірка
Jzс + Jус = 3420,3 + 593,0 = 4013,3 (см4);
Jv + Ju = 415,9 + 3597,4 = 4013,3 (см4).
Jzс + Jус = Jv + Ju.
Ju = Jzс cos2α0 + Jус sin2α0 – Jzсусsin2α0 =
86
87.
= 3420,3 ⋅ cos2(-130 38/)+ 593,0 ⋅sin2(-130 38/) – 729,5⋅sin 2⋅(-130 38/) == 3597,4 (см4);
Jv = Jyс cos2α0 + Jzс sin2α0 + Jzсусsin2α0 =
= 593,0 ⋅ cos2(-130 38/)+ 3420,3 ⋅sin2(-130 38/) + 729,5 ⋅sin 2⋅(-130 38/) =
= 415,9 (см4);
Ju ≡ Ju; Jv ≡ Jv.
Отже, розрахунки виконані правильно.
Визначення осьових моментів опору та головних радіусів інерції
перерізу
Моменти опору (формули 4.25)
I
3597.4
Wu = u =
= 223,3 см3;
vmax 16.11
I
415.9
= 54,2 см3,
Wv = v =
u max 7.67
де vmax ( u max ) – відстань від головної осі v (u) до найбільш віддаленої від
неї точки перерізу за модулем.
Вказівка. Для визначення vmax та u max необхідно провести через точки
перерізу прямі таким чином , щоб вони торкались перерізу і були
паралельні відповідній осі. vmax та u max визначаються вимірюванням
відповідного відрізку на кресленні.
Головні радіуси інерції (формула 4.24)
Ju
Ju
3597.4
iu =
=
=
= 8,62 см;
A
A1 + A2 + A3
24.5 + 13.9 + 10
Jv
Jv
415.9
=
=
= 2,93 см.
A
A1 + A2 + A3
24.5 + 13.9 + 10
В додатку В приведена інструкція до розрахунку геометричних
характеристик плоских перерізів в середовищі “КОМПАС 5.11”.
Розбіжності між аналітичним розрахунком та за допомогою ЕОМ зазвичай
не перевищують 2%.
Приклад (скопійовані в буфер обміну та вставлені в документ
результати розрахунків).
iv =
Площадь
S = 49.4514 см2
В центральной системе координат:
Осевые моменты инерции
Jx = 3442.67 см4
Jy = 615.166 см4
Центробежный момент инерции Jxy = 746.913 см4
В главной центральной системе координат:
Осевые моменты инерции
Jx = 3627.84 см4
Jy = 429.989 см4
Угол наклона главных осей
A = -13.9242°
87
88.
5 КРУЧЕННЯ5.1 Короткі теоретичні відомості
5.1.1 Напруження і деформації при крученні стержнів круглого
поперечного перерізу
Деформація кручення бруса має місце тоді, коли на них діють пари
сил, розташованих у площинах, перпендикулярних до осі бруса.
Деформація
при
крученні
виявляється
у
взаємному
повороті перерізів бруса і
ϕ
ϕ+dϕ
вимірюється у кутових одиницях
(радіанах). Кут повороту двох
крайніх перерізів, розташованих
на відстані l один від одного,
називають
повним
кутом
закручування ϕl або просто ϕ
(рис. 5.1). Кут закручування,
Рисунок 5.1
віднесений до одиниці довжини
бруса, називається відносним
кутом закручування
dϕ
θ=
.
(5.1)
dx
Зовнішній момент, що прикладений до будь-якого перерізу бруса і
викликає деформацію бруса, називають скручувальним моментом Мк , а
внутрішній силовий фактор називається крутним моментом Мх .
У розглядуваному брусі (рисунок 5.1) в будь-якому поперечному
перерізі крутний момент Мх дорівнює скручувальному моментові Мк .
Початкова твірна після деформації набуде вигляду Е, А, В, С. На відстані x
від закріпленого кінця бруса виділимо елемент завдовжки dx (рис. 5.1, 5.2).
Як видно із рисунка 5.2
r dϕ
γ max =
,
(5.2)
dx
ρ dϕ
,
(5.3)
dx
де ρ − відстань від точки перерізу до осі бруса, r = d / 2 −радіус перерізу, d
− діаметр бруса, γmax, γ − відносний зсув на поверхні і на віддалі ρ від осі
бруса, відповідно.
Використовуючи закон Гука при зсуві, для дотичних напружень при
крученні отримаємо вираз
γ=
88
89.
dϕG = ρ ⋅G ⋅ θ.
dx
(5.4)
У площині поперечного перерізу на
відстані ρ від осі бруса виділимо
елементарну площадку dА. Зусилля, що
припадає на цю площадку, дорівнює τ⋅dА,
а момент цього зусилля відносно осі бруса
дорівнює τ⋅ρ⋅dА. Склавши суму зусиль
отримаємо величину крутного моменту
τ = γ ⋅G = ρ
M x = ∫ τ ⋅ ρ ⋅ dА .
(5.5)
А
Підставивши значення τ із (5.4),
матимемо
M x = ∫ ρ 2 ⋅ G ⋅ θ ⋅ dА = G ⋅ θ ∫ ρ 2 dА . (5.6)
А
А
Як показано в розділі 4 (формула 4.6)
полярний момент інерції
I p = ∫ ρ 2 dА ,
Рисунок 5.2
А
тому (5.6) запишемо у вигляді
θ=
Mx
.
G ⋅I p
(5.7)
Підставивши це значення θ у вираз (5.4) матимемо
τ=
Mx
ρ.
Ip
(5.8)
π ⋅ d4
Для круглого поперечного перерізу I p =
.
32
Користуючись цією формулою, легко визначити величину
напружень в будь-якій точці перерізу, розташованій на відстані ρ від осі
бруса. Максимальні напруження діють у точках, які розташовані на
контурі поперечного перерізу бруса (рисунок 5.2), для яких ρmax = r.
Величина максимальних напружень
89
90.
Mxr.
Ip
Замінемо величну Ip/r полярним моментом опору. Тоді для круглого
поперечного перерізу
M
τ max = x .
(5.9)
Wp
τ max =
З формули (5.8) видно, що напруження τ змінюються прямо
пропорційно відстані ρ від осі бруса. Розподіл дотичних напружень по
перерізу бруса наведено на рисунку 5.3. Згідно з законом парності
дотичних напружень, такі самі напруження діятимуть і в поздовжніх
перерізах бруса (рисунок 5.3).
Таким чином при крученні бруса виникає
плоский напружений стан − чистий зсув
(рисунок 5.3). Для елемента біля поверхні бруса
взаємне положення головних площадок і
площадок, на яких діють максимальні дотичні
напруження, показано на рисунку 5.3.
Характер руйнування при крученні
визначається
напруженим
станом
і
Рисунок 5.3
особливостями опору матеріалу бруса лінійним
і кутовим деформаціям. Так, стержні із пластичних матеріалів будуть
руйнуватися по поперечному перерізу від дотичних напружень.
Дерев’яний стержень буде руйнуватися по поздовжніх перерізах, оскільки
дерево погано чинить опір зсуву вздовж волокон. Стержень із крихкого
матеріалу буде руйнуватися по площадках, розміщених під кутом 45° до
осі, тобто перпендикулярних головному напруженню σmax.
Кут закручування ділянки стержня довжиною l знайдемо за
формулою (5.7) з врахуванням (5.1)
l M dx
ϕ=∫ x .
(5.10)
0 I pG
Якщо крутний момент Мх і жорсткість перерізу GIp величини сталі на
ділянці довжиною l, то
M l
ϕ= x .
(5.11)
I pG
Кут закручування стержня, який має n ділянок
n M
ϕ=∑
i =1
90
x i li
I pG
.
(5.12)
91.
5.1.2 Епюри крутних моментівДля розрахунку бруса на кручення (формули 5.7−5.12) необхідно
знати величину крутного моменту Мх в будь-якому поперечному перерізі
бруса. Закон зміни крутних моментів по довжині бруса Мх(х) називають
епюрою крутних моментів. Епюра дає наочне зображення розподілу
крутних моментів вздовж осі бруса. Величину Мх знаходять із умови
рівноваги будь-якої частини бруса, розміщеної з одного боку від перерізу.
Із рівняннь рівноваги випливає, що крутний момент у будь-якому
поперечному перерізі чисельно дорівнює алгебраїчній сумі зовнішніх
моментів, прикладених до бруса справа або зліва від перерізу.
Епюри крутних моментів дають змогу визначити небезпечні
перерізи,
зокрема, якщо брус має сталий поперечний переріз, то
небезпечними будуть перерізи на ділянці, де виникає найбільший крутний
момент.
Крутний момент вважають додатним, якщо результуючий момент
зовнішніх пар, прикладених до розглядуваної частини бруса буде
напрямлений за стрілкою годинника, коли дивитися в торець перерізу, і
навпаки. Користуючись
принципом пом’якшених
граничних
умов,
вважатимемо,
що
у
поперечному перерізі, де
прикладений
скручувальний момент,
значення
крутного
моменту
змінюється
стрибкоподібно.
При
побудові
епюри крутних моментів
їх величини відкладають
Рисунок 5.4
перпендикулярно прямій,
паралельній осі бруса (базі епюри). На рисунку 5.4 приведений приклад
побудови епюри крутних моментів.
5.1.3 Розрахунки на міцність і жорсткість
Для нормальної
задовольнити:
а) умову міцності
роботи
стержнів
91
на
кручення
необхідно
92.
τ max =Mx
≤ [ τ] ,
Wp
(5.13)
θ max =
Mx
≤ [ θ] ,
I pG
(5.14)
б) умову жорсткості
де [τ] − допустиме напруження кручення, яке вибирають залежно від
допустимого напруження на розтяг, умов роботи конструкції та інше.
Наприклад:
для сталей [τ]=(0,55...0,60)[σ]р,
для чавунів [τ]=(1,0...1,2)[σ]р.
В формулі (5.14) [θ] − допустимий кут закручування, нормований
технічними умовами.
Для вала суцільного поперечного перерізу
πd 3 M x
Wp =
=
, звідки
16
[ τ]
d≥3
16M x
.
π[ τ ]
Для трубчастого вала
(
)
M
πD 3
Wp =
1 − α 4 = x , звідки
16
[ τ]
D≥3
16M x
(
π[ τ] 1 − α 4
)
.
де α = d/D.
При розрахунках на жорсткість, враховуючи (5.14) і значення Ip для
πd 4
πD 4
суцільного вала I p =
, для трубчастого вала I p =
1− α4
32
32
знаходимо:
(
для суцільного вала
d≥4
для трубчастого вала
D≥4
)
32 M x
,
Gπ[θ]
32 M x
(
Gπ[θ] 1 − α 4
)
.
Таким чином діаметр вала визначають з умови міцності (5.13) та
умови жорсткості (5.14). За кінцевий розмір беруть більший діаметр.
Часто скручувальні моменти визначають за потужністю N, що
92
93.
передається на вал або знімається з нього і за його кутовою швидкістю ω.У такому випадку скручувальний момент визначають за формулою
Mк =
N
.
ω
(5.15)
Якщо N взяти в ватах, а ω − у радіанах за секунду, то Мк буде в Н⋅м.
5.2 Завдання до розрахунково-графічної роботи
Задача 5. Розрахунок вала на кручення
Для вала, який навантажений тільки крутними моментами (рис. 5.5-
5.8):
а) обчислити величину та напрямок моменту Т0;
б) побудувати епюру крутних моментів;
в) обчислити діаметри ділянок вала із умов міцності і жорсткості, якщо
[θ] = 0,5 0/м;
Для однієї із ділянок розрахунок зробити для двох випадків:
суцільний переріз вала і кільцевий при відношенні внутрішнього
діаметра до зовнішнього α = d/D = 0,8; порівняти вагу валів суцільного
та кільцевого перерізу, зробити висновок щодо раціонального перерізу.
г) побудувати епюру кутів повороту перерізів вала (в градусах).
Таблиця 5.1
Варіант
Т1, Н⋅м
Т2, Н⋅м
Т3,
Н⋅м
а,
м
Матеріал
(сталь)
0
1
2
3
4
5
6
7
8
9
1000
2500
4000
1500
3000
2000
3500
1000
2000
1500
3100
1200
1500
2200
2300
1500
1400
3100
1700
2100
2200
2500
1800
2800
1600
1700
3100
2700
1400
2300
0,1
0,5
0,2
0,4
0,1
0,3
0,5
0,2
0,4
0,1
Ст5
20
30
45
60Г
40Х
20Х
45Х
12ХН3А
30ХСГА
Приклад. Розрахувати вал, зображений на рис. 5.9 на кручення,
згідно з приведеним в задачі 5 порядку розрахунку.
Вихідні дані. Т1 = 1000 Н⋅м; Т2 = 3000 Н⋅м; Т3 = 2000 Н⋅м; [θ] = 1 0/м;
α = d/D = 0,7, сталь 40Х .
93
94.
Знайти: То, Мкр(х), d1, d2, d3, ϕ(х).Розв’язування
Знаходимо невідомий крутний момент Т0, користуючись рівнянням
рівноваги у вигляді
ΣТі = 0;
Нехай Т0 має такий самий напрямок, як і Т1, (правило знаків
приймаємо довільно) тоді
Т1 + Т0 – Т2 – Т3 = 0, звідки
Т0
Т1
Т2
Т2
Т1
а
Т0
а
Т2
а
1,5а
01
Т3
02
Т3
03
0,5а
Т2
Т1
Т3
а
0,5а
Т1
Т0
00
а
1,5а
а
Т3
Т0
а
а
94
04
95.
Т2Т1
Т0
Т3
а
0,5а
а
Рисунок 5.5
Т0
Т1
а
Т2
а
0,5а
Т3
а
Т2
1,5а
Т2
Т1
1,5а
Т0
06
Т3
07
Т3
08
а
1,5а
Т1
Т0
05
1,5а
Т2
Т1
Т3
0,5а
Т0
0,5а
а
09
95
96.
Т1Т0
а
Т3
Т2
0,5а
Рисунок 5.6
96
1,5а
97.
Т2Т1
Т0
а
0,5а
Т3
а
1,5а
а
Т3
а
0,5а
Т0
1,5а
Т2
Т1
1,5а
11
Т0
12
Т3
13
Т0
14
а
Т2
Т1
Т0
0,5а
Т2
Т1
10
1,5а
Т2
Т1
Т3
0,5а
Т3
а
1,5а
Рисунок 5.7
97
98.
Т0Т1
Т3
Т2
0,5м
1м
0,7м
Рисунок 5.8
Т0 = -Т1 + Т2 + Т3 = -1000 + 3000 + 2000 = 4000 Н⋅м.
Будуємо епюру крутних моментів
Знаходимо внутрішні крутні моменти , використовуючи метод
перерізів.
Ділянка АВ
0 ≤ x 1 ≤ 1 м,
МI = -Т1 = -1000 H⋅м.
Ділянка ВС
0 ≤ x2 ≤ 0,5 м,
МII = -Т1 – Т0 = -1000 – 4000 = -5000 H⋅м.
Ділянка СD
0 ≤ x3 ≤ 0,7 м,
МIII = -Т1 – Т0 + Т2 = -1000 – 4000 + 3000 = -2000 H⋅м.
Епюра крутних моментів приведена на рис. 5.10.
М кр
Із умови міцності при крученні τ =
≤ [τ ] знаходимо мінімальне
Wp
значення діаметра ділянок вала суцільного перерізу
16М кр
16 М кр
3
=
[
τ
]
,
звідки
d
=
,
π [τ ]
πd 3
Для трубчастого вала
M кр
16M кр
πD 3
Wp =
1−α 4 =
, звідки D ≥ 3
, де α = d/D.
[τ ]
16
π [τ ]1 − α 4
M
Із умови жорсткості при крученні θ max = x ≤ [θ] знаходимо
I pG
мінімальне значення діаметра ділянок вала, де значення Ip для суцільного
πd 4
πD 4
вала I p =
, для трубчастого вала I p =
1− α4 .
32
32
32M кр
32 ⋅180 ⋅ M кр
d ≥4
Отже, для суцільного вала
=4
,
2 0
Gπ [θ ]
Gπ [θ ]
(
)
98
(
)
(
)
99.
D≥4для трубчастого вала
32 ⋅180 ⋅ M кр
Gπ [θ ](1 − α )
2
0
4
.
Визначення допустимих напружень
Допустимі напруження для сталі 40Х (пластичний матеріал)
дорівнюють (формула 2.20)
[σ ]p = σ н = σ т = 800 = 400 МПа,
n
n
2
[τ] = (0,55...0,60)[σ]р = 0,6⋅400 = 240 МПа.
де σн = σт = 800 МПа − границя текучості сталі 40Х (див. додаток Ж),
n − коефіцієнт запасу міцності при дії на вал статичного навантаження
n = 1,5...2, приймаємо n = 2.
Т1 =1000 Н⋅м
Т2 =3000 Н⋅м
Т0 =4000 Н⋅м
А
В
х1
х3
0,5м
1м
D
С
х2
Т3 =2000 Н⋅м
0,7м
0
0
Мкр , Н⋅м
1000
2000
5000
0
0
0,80
1,24
1,82
Рисунок 5.10
99
ϕ ,0
100.
Ділянка АВ. МI = -1000 H⋅м.Суцільний переріз
умова міцності
16
16 ⋅1000
dI = 3 М I = 3
= 0,0277 (м),
π [τ ]
π ⋅ 240 ⋅10 6
умова жорсткості
32 ⋅180 ⋅ M I
32 ⋅180 ⋅1000
dI ≥ 4
=4
= 0,052 (м),
2 0
Gπ [θ ]
8 ⋅1010 π 2 ⋅1
Приймаємо більший з розрахованих та округляємо його до
стандартного числа d I = 55 мм.
Для трубчастого вала
умова міцності
16 М I
16 ⋅1000
=
DI = 3
= 0,0303 (м),
3
π [τ ]1 − α 4
π ⋅ 240 ⋅10 6 1 − 0,7 4
умова жорсткості
32 ⋅180 ⋅ M I
32 ⋅180 ⋅1000
DI ≥ 4
=
= 0,0557 (м).
4
Gπ 2 [θ 0 ]1 − α 4
8 ⋅1010 π 2 ⋅11 − 0,7 4
Приймаємо більший з розрахованих та округляємо його до
стандартного числа D I = 60 мм.
Внутрішній діаметр трубчатого перерізу dт = DI⋅α = 60⋅0,7= 42 мм.
Порівняємо вагу валів кожного перерізу. Співвідношення мас валів
прямо пропорційне площам їх перерізів при однаковій густині матеріалу ρ
та довжині вала:
mc V c ρ
A l
A
=
= c = c ,
m т V т ρ Aт l Aт
(
)
(
(
)
)
(
)
Ac
dc
(π / 4 ) d c
55 2
=
=
=
=1,65.
A т (π / 4 )( D т 2 − d т 2 ) D т 2 − d т 2 602 − 42 2
2
2
Отже, с точки зору економії матеріалу кільцевий переріз вала є
раціональнішим, оскільки вал буде мати меншу масу в 1,65 рази при
заданій величині α = 0,7.
Подальший розрахунок ділянок вала ведемо за умовою жорсткості,
виходячи із аналізу результатів для першої ділянки.
Ділянка ВС. МII = -5000 H⋅м.
32 ⋅180 ⋅ M II
32 ⋅180 ⋅ 5000
4
d II ≥ 4
=
= 0,0778 (м).
Gπ 2 [θ 0 ]
8 ⋅1010 π 2 ⋅1
Приймаємо d II = 80 мм.
Ділянка СD. МIII = -2000 H⋅м.
100
101.
d III ≥ 432 ⋅180 ⋅ M III
=4
32 ⋅180 ⋅ 2000
Gπ 2 [θ 0 ]
8 ⋅1010 π 2 ⋅1
Приймаємо d III = 65 мм.
Будуємо епюру кутів закручування
Кут закручування знаходимо із виразу
М кр ⋅ l
ϕ=
,
G⋅I p
де l – довжина відрізка вала; I p =
= 0,0618 (м).
π d4
– полярний момент інерції.
32
Визначимо кут закручування граничних перерізів на кожній ділянці
відносно перерізу в точці А.
Ділянка АВ. 0 ≤ x1 ≤ 1 м, МI = -1000 H⋅м, d I = 55 мм.
I p1 =
πd14
=
π ⋅ 0,055 4
= 8,98⋅10-7 (м4),
32
32
⋅1
− 1000 ⋅1
ϕ BA = М I =
= −0,0139 рад = 0,800.
10
−
7
G ⋅ I p1 8 ⋅10 ⋅ 8,98 ⋅10
Ділянка ВС. 0 ≤ x2 ≤ 0,5 м, МII = -5000 H⋅м, d II = 80 мм.
I p2 =
πd 24 π ⋅ 0,084
=
= 4,02⋅10-6 (м4),
32
32
⋅ 0,5
− 5000 ⋅ 0,5
ϕ CA = ϕ BA + М II
= −0,0139 +
=
G ⋅ I p2
8 ⋅1010 ⋅ 4,02 ⋅10 −6
= − 0,0139 − 0,0078 = −0,0217 рад = -1,240,
Ділянка СD. 0 ≤ x3 ≤ 0,7 м, МIII = -2000 H⋅м, d III = 65 мм.
I p3 =
πd 34
=
π ⋅ 0,065 4
= 1,75⋅10-6 (м4),
32
32
⋅ 0,7
− 2000 ⋅ 0,7
ϕ DA = ϕ CA + М III
= −0,0217 +
=
G ⋅ I p3
8 ⋅1010 ⋅1,75 ⋅10 −6
= −0.0217 − 0.0100 = −0,0317 рад = -1,820.
Виходячи із отриманих значень ϕі (і =1, 2, 3), будуємо епюру кутів
закручування вала (рис 5.10), враховуючи лінійний вид графіка.
101
102.
6 ЗГИН6.1 Короткі теоретичні відомості
6.1.1 Основні поняття
Розглянемо призматичний
брус з прямою віссю, на який діє
ряд
зрівноважених
сил,
розташованих в одній площині,
що проходить через вісь бруса
(рисунок 6.1). У такому випадку
брус зазнаватиме деформації
згину.
Площину,
в
якій
розташовані
сили,
що
викликають згинання бруса,
називають
площиною
дії
Рисунок 6.1
згинальних сил. Площину, що
проходить через вісь бруса і
головні осі інерції поперечних перерізів, називають головною площиною
бруса.
Якщо площина дії згинальних сил збігається з головною площиною,
то і згин буде відбуватися в цій же площині. Такий згин називається
прямим або плоским згином.
Будь-який брус з прямолінійною віссю, що зазнає деформації згину,
називають балкою. Балка, жорстко закріплена одним кінцем (рисунок
6.2, а), або ділянка балки, один кінець якої без опори (рисунок 6.2, б,
ділянка l3) називається консоллю. На рисунку 6.2, б зображено балку на
трьох опорах, навантажену зосередженими силами Р1, Р2 , рівномірно
розподіленим навантаженням інтенсивністю q і парою сил М. Відстань між
двома суміжними опорами балок називають прогоном. Кінець балки, який
Рисунок 6.2
звисає називають консольним кінцем.
6.1.2 Напруження при чистому згині
Згин балки, при якому згинальний момент сталий по довжині бруса,
102
103.
а поперечна сила дорівнює нулю,називається чистим згином. Чистий згин
можна отримати, якщо прикласти до бруса
в кінцевих перерізах рівні за величиною і
протилежного напрямку пари сил, які
діють в площині симетрії бруса (рисунок
6.3, а) або навантажити брус силами
(рисунок 6.3, б). Дослід показує, що при
чистому згині поздовжні лінії ab i aobo ,
нанесені
на
поверхню
бруса,
викривляються, а поперечні aoa i bob
повертаються, залишаючись прямими і
Рисунок 6.3
перпендикулярними
зігнутим
лініям
(рисунки 6.4, а, б).
Поздовжні
волокна
бруса
зазнають простого
розтягу
або
стиску,
не
спричинюючи
взаємного
бокового стиску.
По висоті перерізу
бруса деформація
розтягання
і
стискання
змінюється
безперервно.
Отже, в середині
бруса існує шар,
який відділяє зону
розтягання
від
Рисунок 6.4
зони
стискання.
Волокна цього шару не зазнають ніякої деформації. Такий шар називають
нейтральним. Лінія перерізу нейтрального шару з площиною поперечного
перерізу бруса називається нейтральною лінією.
Визначимо величину нормальних напружень (рисунок 6.4, б), які
виникають при чистому згині. Для цього розглянемо деформацію ділянки
бруса, вирізаної двома перерізами, розташованими на відстані dx один від
одного (рисунок 6.4, а). Нейтральний шар на цьому рисунку зображений
лінією aobo = dx.
Позначимо радіус кривизни нейтрального шару через ρ, а кут
повороту перерізу n-n відносно перерізу m-m − через dθ. Розглянемо
відносне видовження довільного волокна ab, розташованого на відстані у
103
104.
від нейтрального шару (рисунок 6.4, б).∆l a1b1 − ab (ρ + y )dϕ − ρdϕ y
(6.1)
=
=
= .
l
ab
ρdϕ
ρ
За законом Гука нормальне напруження в волокні ab буде рівне
y
(6.2)
σx = E ⋅ εx = E ⋅ .
ρ
Розглянемо переріз m-m (рисунок 6.4, б). Візьмемо на площині
перерізу елементарну площадку dА з координатами y і z. На цю площадку
діє нормальне зусилля dN = σ x dА . Сума моментів елементарних
внутрішніх сил dN відносно осі z дає величину внутрішнього згинального
моменту, який діє в цьому перерізі
(6.3)
M z = ∫ σ x ⋅ y ⋅ dА .
εx =
А
Підставимо значення σх із (6.2)
E
M z = ∫ y 2 dА
ρА
або
Mz =
E
⋅Iz ,
ρ
де I z = ∫ y 2 dА − осьовий момент інерції бруса відносно осі z.
А
Перепишемо (6.3) у вигляді
1 Mz
.
(6.4)
=
ρ EI z
Вираз (6.4) – це залежність між згинальним моментом і кривизною
осі бруса при чистому згині. Добуток EIz називається жорсткістю
поперечного перерізу бруса при згині. Підставивши (6.4) в (6.2) знайдемо
M
(6.5)
σx = z ⋅ y .
Iz
Вияснимо положення осі z − нейтральної лінії перерізу. При чистому
згині нормальна сила в перерізі дорівнює нулю, тобто
E
N = ∫ σ x dА = ∫ y ⋅ dА = 0.
ρА
А
Оскільки E ρ ≠ 0 , то ∫ y ⋅ dА = 0 . Цей інтеграл являє собою статичний
А
момент площі перерізу бруса відносно осі z, оскільки ∫ y ⋅ dА = 0 , то вісь z
А
проходить через центр ваги перерізу.
При чистому згині дорівнює нулю згинальний момент відносно осі у,
тобто
E
M y = ∫ σ x z ⋅ dА = ∫ y ⋅ z ⋅ dА = 0 .
ρА
А
104
105.
Оскільки відцентровий момент I zy = ∫ zydА = 0 , то вісь z є головною.А
Отже нейтральна лінія при згині збігається з головною віссю перерізу.
Як видно із (6.5) нормальні напруження змінюються по висоті
перерізу за лінійним законом. На рисунку 6.5 показані епюри нормальних
напружень. Найбільші напруження виникають у точках найбільш
віддалених від нейтральної лінії, для яких y = ymax . Величину найбільших
напружень у перерізі визначають за формулою
M
(6.6)
σ max = z ⋅ y max .
Iz
Величина
I
Wz = z
y max
називається осьовим моментом опору перерізу. Поняття моменту опору
вводиться, як правило, для перерізів, симетричних відносно нейтральної
осі (рисунок 6.5, а, б). Для таких перерізів формула (6.6) записується у
вигляді
M
σ max = z .
(6.7)
Wz
Якщо переріз несиметричний відносно нейтральної лінії, то
σ max =
Mz
yA ,
Iz
σ min =
Mz
yB ,
Iz
ymax
y’max ymax
де уА , уВ −координати найбільш віддалених точок перерізу.
105
Рисунок 6.5
(6.8)
106.
6.1.3 Поперечний згин. Дотичні напруженняПри поперечному згині бруса в його перерізах, крім згинального
моменту діє поперечна сила. У цьому випадку, крім нормальних
напружень від згинального моменту, у перерізах виникають також дотичні
напруження від поперечної сили. Їх розраховують за формулою
Журавського
τ yx =
Q y ⋅ S z*
b⋅ Iz
,
(6.9)
y
h/2-y
yц.в
y
yц.в
h
де Qy − поперечна сила в перерізі, b− ширина перерізу в тому місці, де
треба обчислити дотичні напруження, S*z − абсолютна величина
статичного моменту
площі відносно осі z
тієї частини площі
перерізу A*, яка
відсікається прямою,
паралельною
нейтральній осі z,
проведеній
через
точку,
в
якій
визначається
Рисунок 6.6
дотичне напруження,
Iz − момент інерції перерізу відносно осі z (рисунок 6.6, а).
Оскільки для перерізу Qy і Iz величини сталі, то закон розподілу
дотичних напружень по висоті перерізу визначається відношенням S z* / b .
Наприклад, для прямокутного перерізу
1 h
h
b h
S z* = b − y y + − y =
2
2 2
− y2 ,
2 4
2
b ⋅ h3
.
12
Підставивши значення S*z і Iz в (6.25), отримаємо
Iz =
y2
3 Qy
1 − 4 2 .
τ yx =
2 b⋅ h
h
Отже, по висоті прямокутного перерізу дотичні напруження
змінюються за параболічним законом. Найбільшого значення дотичні
106
107.
напруження досягають в точках, розташованих на нейтральній лінії приy=0 (рисунок 6.6).
6.1.4 Аналіз напруженого стану при згині.
Розрахунки на міцність
Як видно із рисунка 6.5 і рисунка 6.6 в точках, які лежать на верхній
і нижній границях поперечного перерізу, мають місце тільки нормальні
напруження і в цих точках вони набувають найбільшого значення. Таким
чином для цих точок умову міцності можна записати у вигляді
σ max =
Mz
≤ [σ] .
Wz
(6.10)
Якщо матеріал крихкий і по різному чинить опір розтяганню і
стисканню, то балки із такого матеріалу мають несиметричний по
відношенню до нейтральної лінії переріз (рис. 6.5, г). Такі балки
розміщують так, щоб більші за абсолютною величиною напруження були
стискувальні, а менші − розтягувальні (рисунок 6.5, д). Умови міцності для
таких випадків приймають вигляд
M
σ max = σ A = z ⋅ y A ≤ [σ ] p ,
Iz
M
(6.11)
σ min = σ B = z ⋅ y B ≤ [σ ]ст ,
Iz
де [σ]р − допустиме напруження при розтягу, а [σ]с − допустиме
напруження при стиску.
Таким чином для балок із пластичних матеріалів, які однаково
працюють на розтяг і стиск, доцільно вибирати перерізи, симетричні відносно їх нейтральних осей. При цьому забезпечується однаковий запас міцності по стиснутих і розтягнутих волокнах. Якщо крім умови міцності
виходити ще із вимоги мінімальної маси балки, то найбільш раціональним
буде переріз, який при заданій величині моменту опору Wz має найменшу
площу перерізу А або при заданій площі А − найбільший момент опору Wz.
Порівнюючи з цих позицій, наприклад, прямокутний переріз з
двотавровим, неважко переконатись в перевазі останнього.
У балки прямокутного перерізу матеріал в області нейтральної лінії
повністю не використовується, оскільки знаходиться в зоні з малими
напруженнями. У двотаврової балки більша частина матеріалу розміщена в
найбільш напруженій зоні. Тому при однаковій міцності двотаврова балка
в 2...3 рази легша прямокутної. В точках перерізу, розміщених на
нейтральній осі, діють тільки дотичні напруження (рисунках 6.5 і 6.6),
тому умова міцності для цих точок буде така:
107
108.
τ max =Q y ⋅ S zmax
b⋅ Iz
≤ [ τ] .
(6.12)
В решти точок перерізу при поперечному
згині має місце плоский напружений стан, тобто
одночасно
діють
дотичні
і
нормальні
напруження (рисунок 6.7). Умова міцності
записується у вигляді
σ екв ≤ [σ ] .
(6.13)
Головні напруження в цих точках визначаються
за формулами
σ
1
2
σ 1 = x + σ x2 + 4τ yx
,
2 2
σ 2 = 0,
σ3 =
σx
2
−
Рисунок 6.7
(6.14)
1
2
σ x2 + 4τ yx
,
2
Еквівалентне напруження σекв вибирається в залежності від
прийнятої теорії міцності.
Для пластичних матеріалів − за третьою теорією міцності.
III
2
σ екв
= σ 1 − σ 3 = σ x2 + 4τ yx
.
(6.15)
Для крихких матеріалів за теорією Мора
σ екв = σ 1 − m σ 3 =
де m =
[σ ] p
1− m
1+ m
σx +
σ x2 + 4τ 2yx ,
2
2
(6.16)
.
[σ ]–
Більшість розрахунків на міцність при згині роблять за формулою
(6.10). Для цього необхідно побудувати епюру згинальних моментів Mz і
по ній визначити небезпечний переріз, тобто той переріз, в якому Mz має
найбільше значення.
Можливі випадки, коли при великих поперечних силах в перерізах
балки діють незначні згинальні моменти (короткі балки). В цьому випадку
підбирають переріз за (6.10) і обов’язково перевіряють чи виконується
умова міцності (6.12) для точок, які лежать на нейтральній лінії. Перерізи,
в яких діють найбільша поперечна сила і найбільший згинальний момент
108
109.
можуть збігатися.В балках з тонкостінним перерізом небезпечною може бути точка
перерізу, розміщена в місці переходу стінки в полицю (рисунок 6.5, г). Тут
має місце плоский напружений стан, тобто σх ≠ 0, τух ≠ 0,σу = 0.
Для перевірки міцності таких балок необхідно:
а) визначити переріз, в якому діє найбільший згинальний момент і за (6.10)
підібрати переріз;
б) знайти переріз балки, в якому одночасно Mz і Qy мають найбільші
значення. Такий вибір не завжди однозначний, тому бувають випадки,
коли таких перерізів більше одного;
в) перевірити за формулами (6.15) або (6.16), залежно від матеріалу балки,
чи виконуються ці умови міцності для небезпечної точки. Якщо умови
міцності не виконуються, то збільшують розміри перерізу, або
вибирають за сортаментом більший номер профілю.
6.1.5 Рівняння пружної лінії зігнутої балки
В інженерній практиці розраховують балки не тільки на міцність, але
й на жорсткість. При згині жорсткість характеризується здатністю балки
чинити опір викривленню. При деформації в межах пружності зігнуту вісь
балки називають пружною лінією. Відхилення будь-якої точки осі балки
від первісної прямої називають прогином. Кут повороту будь-якого
перерізу балки відносно його початкового положення називають кутом
повороту перерізу.
В п. 6.1.2 встановлено, що кривизна пружної лінії прямо
пропорційна згинальному моменту (6.4)
1 Mz
.
=
ρ EI z
З курсу вищої математики відомо, що
d2y
1
dx 2
,
=±
3
ρ
dy 2 2
1 +
dx
таким чином
d2y
dx 2
=±
3
Mz
.
EI z
(6.17)
dy 2 2
1 +
dx
Рівняння (6.17) називають диференціальним рівнянням пружної лінії
109
110.
і інтегрування цього рівняння пов’язане з великими труднощами. Тому в2
dy
тих випадках, коли прогини невеликі, величиною порівняно з
dx
одиницею можна знехтувати. Тоді дістанемо наближене диференціальне
рівняння пружної лінії у вигляді
Mz
d2y
.
(6.18)
=
±
EI z
dx 2
Знак кривизни може не збігатися зі знаком згинального моменту і
залежить від напрямку координатних осей. Якщо вісь у направити вверх а
вісь х вправо, то знаки у″ і Мz збігаються, тому в (6.18) запишемо знак
“плюс”
M
y"= z .
(6.19)
EI z
Інтегруючи це рівняння один раз, дістанемо рівняння кутів повороту
M
dy
(6.20)
= ∫ z dx + C1 .
θ=
dx
EI z
Інтегруючи вдруге, знайдемо
M
y = ∫ dx ∫ z dx + C1x + C 2 ,
(6.21)
EI z
де С1 і С2 −сталі інтегрування, які можна знайти із граничних умов.
6.1.6 Визначення кутових та лінійних переміщень методом
початкових параметрів
Визначення переміщень методом безпосереднього інтегрування
диференційного рівняння пружної лінії в випадку балок з великою
кількістю ділянок ускладнено. Ці труднощі пов'язані не з інтегруванням
диференціальних рівнянь, а з технікою визначення довільних сталих
інтегрування − складанні і розв'язуванні систем лінійних алгебраїчних
рівнянь. Так, якщо балка має n ділянок, то інтегрування диференціального
рівняння (6.19) необхідно виконувати для кожної ділянки. В такому
випадку буде 2n сталих інтегрування, які визначають із умов на межах
ділянок. Тому на практиці часто використовують метод початкових
параметрів, який базується на диференціальних залежностях, справедливих
для будь-якого перерізу балки між кутом повороту θ та моментом Mz і
дозволяє при будь-якій кількості ділянок звести розв'язання до визначення
всього двох сталих − прогину і кута повороту перерізу в початку
координат.
M z dθ d 2 y
=
=
,
(6.22)
EI z dx dx 2
між прогином y та кутом повороту θ є залежність
110
111.
dy.
(6.23)
dx
При використанні цього методу початок координат розміщують в
крайньому лівому перерізі і він є загальним для всіх ділянок балки.
Згинальний
момент
визначають
як
алгебраїчну
суму
моментів
всіх
сил
розміщених зліва від
перерізу. При цьому
зовнішній зосереджений
момент M1 (рисунок 6.8),
прикладений
на
відстані a від початку
координат, множать на
величину (x-a)0, яка
дорівнює
1,
а
розподілене
навантаження, у випадку
Рисунок 6.8
його обриву (наприклад
при x = d) продовжують до перерізу, в якому визначають переміщення і
починаючи з перерізу x = d вводять розподілене навантаження
протилежного напрямку. Інтегрування диференціального рівняння
виконують не розкриваючи дужок.
Напишемо вираз для згинального моменту в перерізі з координатою
“x” (рисунок 6.8)
0
M z = M 0 + Q0 x + M 1 (x − a ) + R A (x − b1 ) +
θ=
q (x − c )
q (x − d )
+ P1 (x − b2 ) +
−
.
(6.24)
2
2
Проінтегруємо (6.24) з врахуванням (6.22) один раз, одержимо
рівняння кутів повороту для балки сталої жорсткості
Q0 x 2 n
1
θ = θ0 +
M 0x +
+ ∑ M i (x − ai ) +
EI z
2
i =1
n
(x − bi )2 n (x − ci )3 n (x − d i )3
+ ∑ Pi
+ ∑ qi
− ∑ qi
.
(6.25)
2!
3!
3!
i =1
i =1
i =1
Інтегруючи вдруге, одержимо рівняння прогинів
(x − ai )2
1 M 0 x 2 Q0 x 3 n
y = y0 +
+
+ ∑M i
+
EI z 2!
3!
2!
i =1
2
111
2
112.
n+ ∑ Pi
(x − bi )3
n
+ ∑ qi
(x − ci )4
n
− ∑ qi
(x − d i )4
.
(6.26)
В перерізі балки, де взято початок координат, в загальному випадку
будуть діяти поперечна сила, згинальний момент, а також будуть мати
місце кут повороту і прогин, які ми позначили відповідно Q0 , M0 , θ0 , y0 і
називатимемо їх далі початковими параметрами (рисунок 6.8). Для балки,
показаної на рисунку 6.8, Q0=P, M0=M, а значення θ0 і y0 можна визначити
із умов закріплення
y(b1) = 0, y(l) = 0.
i =1
3!
i =1
4!
i =1
4!
Слід відмітити, що при визначенні кута повороту і прогину в перерізі
з координатою x в рівняння (6.25) і (6.26) входять тільки ті навантаження,
які знаходяться між початком координат і перерізом.
6.2 Завдання до розрахунково-графічної роботи
Задача 6. Розрахунок балки на міцність і жорсткість
Для балки, що навантажена за заданою схемою (рис. 6.9 – 6.11):
а) побудувати епюри поперечних сил та згинальних моментів і визначити
небезпечні поперечні перерізи;
б) підібрати круглий, прямокутний із співвідношенням сторін h:b=2 і
двотавровий переріз за умовою міцності при чистому згині;
в) порівняти вагу балок кожного перерізу, зробити висновок щодо
раціонального перерізу;
г) перевірити міцність двотаврової балки за максимальними дотичними
напруженнями;
д) побудувати епюри нормальних та дотичних напружень в небезпечному
поперечному перерізі балки та провести повну перевірку міцності за
третьою теорією міцності, уточнити номер двотавра;
е) із використанням методу початкових параметрів за допомогою ЕОМ
побудувати пружну лінію балки та графік кутів повороту перерізу (додаток Г);
ж) перевірити балку на жорсткість та підібрати необхідний за умовою
жорсткості переріз.
Матеріал балки – сталь Ст3, допустимий прогин [f] = l/400, де l –
довжина балки. Інші дані для розрахунків взяти з таблиці.
Таблиця 6.1
Варіант q, кН/м
P, кН
M, кН⋅м
0
30
15
12
1
26
20
16
2
20
10
20
112
113.
34
5
6
7
8
9
14
30
20
10
24
16
30
25
20
16
30
24
28
20
10
14
10
15
18
25
10
q
P
М
2м
00
2м
q
2м
М
P
3м
q
2м
1м
02
М P
2м
1м
3м
q
3м
01
P
1м
1м
М
03
1м
04
113
114.
q1м
М
1м
P
2м
Рисунок 6.9
114
2м
115.
qМ
2м
1м
М
P
1м
2м
P
2м
2м
1м
2м
2м
q
1м
07
1м
P
1м
1м
1м
М
М
2м
2м
Рисунок 6.10
115
08
2м
q
1м
1м
q
P
М
06
q
1м
05
1м
P
09
116.
qP
1м
М
2м
1м
2м
q
P
2м
10
2м
М
1м
1м
q
P
1м
М
3м
1м
13
М P
3м
2м
q
М
P
1м
12
2м
q
1м
11
3м
Рисунок 6.11
116
14
1м
117.
Приклад. Розрахувати балку на згин, згідно з приведеним в умові задачі 6порядком розрахунку.
q
М
2м
2м
2м
F
2м
Рисунок 6.12
Вихідні дані: q = 10 кН/м, М = 40 кН⋅м, F = 20 кН.
Матеріал балки – сталь Ст5, допустимий прогин [f] = l/400,
Знайти: M(x), Q(x), d, h, b, № двотавра, m1:m2:m3, τmax, τ(y), σ(y),
III
σ екв max , y(x), θ(x), ymax – ?
Розв’язування
Побудова епюр поперечних сил та згинальних моментів
Визначаємо опорні реакції із рівнянь рівноваги статики.
ΣМА = 0;
-M – F⋅(2+2) – q⋅2(2 + 1) + RB(2 + 2 + 2) = 0;
RB = [M + F⋅(2+2) + q⋅2(2 + 1)]/6 = [40 + 20⋅4 + 10⋅6)]/6 = 30 кН.
ΣМВ = 0;
-M + F⋅2 + q⋅2(2 + 1) – RA(2 + 2 + 2) = 0;
RA = [-M + F⋅2 + q⋅2(2 + 1) ]/6 = [-40 + 20⋅2 + 10⋅6)]/6 = 10 кН.
Перевірка.
ΣFy = 0;
RА – q⋅2 – F + RB = 10 – 10⋅2 –20 + 30 = 0.
Розділяємо балку на чотири ділянки і складаємо рівняння
поперечних сил та згинальних моментів для кожної з них.
Ділянка ЕА (розглядаємо справа наліво).
0 м ≤ х 1 ≤ 2 м.
Q(x1) = 0 кН;
М(x1) = М = 40 кН⋅м.
Ділянка AD (розглядаємо справа наліво).
0 м ≤ х 2 ≤ 2 м.
Q(x2) = RА = 10 кН;
М(x2) = М + RА⋅x2 = 40 + 10x2;
при x2 = 0 М(0) = 40 кН⋅м,
при x2 = 2 М(2) = 40 + 10⋅2 = 60 кН⋅м.
Ділянка BC (розглядаємо зліва направо).
0 м ≤ х 3 ≤ 2 м.
Q(x3) = -RB = -30 кН;
117
118.
RA=10 кНМ=40 кН⋅м
Е
A
q=10 кН/м P=20 кН
RB=30 кН
D
В
С
х2
х1
2м
х4
2м
а)
х3
2м
2м
Qy , кН
10
0
б)
0
10
30
1м
30
Mz , кН⋅м
60
65
60
40
40
0
в)
0
у(х), мм
34
г)
0
0
0
19
22
θ(х), рад
0
0
0,005
0,021
0,014
Рисунок 6.13
118
19
0,006
x
0,011
x
д)
119.
М(x3) = RB⋅x3 = 30x3;при x3 = 0 М(0) = 0 кН⋅м,
при x3 = 2 М(2) = 30⋅2 = 60 кН⋅м.
Ділянка CD (розглядаємо зліва направо).
0 м ≤ х 4 ≤ 2 м.
Q(x4) = -RB + F + q⋅x4 = -10 + 10⋅x4;
М(x4) = RB⋅(x3 + 2) – F⋅x4 – q⋅(x4)2/2 = 60 + 10x4 – 5⋅(x4)2;
при x4 = 0 Q(0) = -10 кН;
М(0) = 60 кН⋅м.
при x4 = 2 Q(2) = -10 + 10⋅2 = 10 кН;
М(2) = 60 + 10⋅2 – 5⋅22 = 60 кН⋅м.
Оскільки епюра Q(x4) перетинає вісь х, то в точці перетину епюра
М(x4) набуватиме екстремального значення.
Q(x4) = 0;
-10 + 10⋅x4 = 0,
звідки x4 = 1 м;
М(1) = 60 + 10⋅1 – 5⋅12 = 65 кН⋅м.
За отриманими значеннями будуємо епюри поперечних сил Q(х) та
згинальних моментів М(х).
Визначення небезпечних поперечних перерізів по довжині балки
За максимальними нормальними напруженнями σmax небезпечний
переріз знаходиться в точці, де діє максимальний згинальний момент (за
модулем)
Мmax = 65 кН⋅м.
За максимальними дотичними напруженнями τmax небезпечний
переріз знаходиться в точці, де діє максимальна поперечна сила (за модулем
Qmax) = 30 кН.
III
За максимальними еквівалентними напруженнями σ екв
max небезпечний переріз знаходиться в точці, де одночасно діє максимальний
згинальний момент (за модулем) та максимальна поперечна сила (за
Вказівка
модулем.). Якщо ці точки не збігаються, то для визначення небезпечного
перерізу необхідно розрахувати низку перерізів, в яких ймовірно
III
досягають максимального значення σ екв
max або будувати епюру
III
розподілу σ екв
(х). Для спрощення оптимального пошуку в
III
навчальних цілях розрахунок σ екв
max можна виконати для
перерізу, в якому чисельно сума Q(x) + M(x) набуває
максимального значення.
Отже небезпечний переріз знаходиться в т. С, де
Q(x) = 30 кН , M(x) = 60 кН⋅м,
Q(x) + M(x) = 30 + 60 = 90 → max.
119
120.
Проектний розрахунок перерізів за умовою міцності при чистомузгині
Мmax = 65 кН⋅м.
Визначаємо допустимі напруження.
Допустиме нормальне напруження для сталі Ст5 (пластичний
матеріал) дорівнює (формула 2.20)
[σ ] = σ н = σ т = 320 = 160 МПа,
n
n
2
де σн = σт = 320 МПа − границя текучості сталі 5 (див. додаток Ж),
n − коефіцієнт запасу міцності при дії на конструкцію статичного
навантаження n = 1,5...2, приймаємо n = 2.
Таким чином [σ ] = 160 МПа.
Допустиме дотичне напруження для сталі (пластичний матеріал)
приймаємо
[τ ] = 0,5... 0,6[σ ] = 0,5 ⋅160 = 80 МПа.
За формулою (6.10) знаходимо необхідний момент опору
M
65 ⋅103
W zн ≥ z =
= 406,25 ⋅10 −6 (м3) = 406,3 см3.
(6.27)
6
[σ ] 160 ⋅10
За сортаментом підбираємо двотавр №27а (додаток Д), для якого
W z = 407 см3, S zmax = 229 см3, Іz = 5500 см4, А = 43,2 см2, h = 27 см, b =
= 135 мм, d = 6 мм, t = 10,2 мм.
Для круглого перерізу момент опору
32W z
πd 3
Wz =
, звідки d = 3
.
π
32
Необхідний діаметр з урахуванням (6.27)
32W zн 3 32 ⋅ 406,3
dн = 3
=
=16,06 см.
π
π
Округляємо діаметр до стандартного числа та приймаємо d = 165 мм.
Для прямокутного перерізу момент опору (розміщуємо переріз
раціонально)
bh 2
Wz =
, звідки при умові h = 2b
6
3W z
b(2 b )2 2 b 3
Wz =
=
,
b=3
.
6
3
2
Необхідний діаметр з урахуванням (6.27)
3W zн 3 3 ⋅ 406,3
bн ≥ 3
=
= 8,49 см.
2
2
Округляємо ширину b та приймаємо b = 85 мм. Висота прямокутника
h = 2b = 170 мм.
120
121.
Вибір раціонального перерізуПорівняємо вагу балок кожного перерізу. Співвідношення мас балок
прямо пропорційне площам їх перерізів при однаковій густині матеріалу ρ
та довжині балки:
m1 V1 ρ A1l A1
;
=
=
=
m 2 V 2 ρ A2 l A2
(π / 4 )d
A
= к =
m двотавр Aд
Aд
m кругл
2
=
π ⋅d 2
4 Aд
=
π ⋅16,5 2
4 ⋅ 43,2
= 4,95;
A п bh b ⋅ h 8,5 ⋅17
=
=
=
= 3,34.
m двотавр Aд A д
Aд
43,2
Отже, с точки зору економії матеріалу двотавровий переріз балки є
раціональнішим, оскільки балка буде мати найменшу масу. Круглий
переріз із розрахованих матиме найбільшу масу (майже в 5 разів ніж
двотавровий).
Перевірка міцності двотаврової балки за максимальними дотичними
напруженнями
Qmax = 30 кН.
Максимальні дотичні напруження згідно з формулою Журавського
рівні
Q S max
30 ⋅103 ⋅ 229 ⋅10 −6
τ max = max z
=
= 20,8 ⋅10 6 Па.
−
−
8
3
Izd
5500 ⋅10 ⋅ 6 ⋅10
Перевіримо виконання умови міцності
τ max = 20,8 МПа < [τ] =80 МПа.
Таким чином, міцність балки за максимальними дотичними
напруженнями забезпечена.
Вказівка. При невиконанні умови міцності.
Якщо максимальне дотичне напруження τ max не перевищує
допустиме [τ] більше ніж на 5% (τ max < 1,05[τ]), то розміри
перерізу (№ двотавра) залишають без змін з відповідним
обґрунтуванням. Якщо τ max перевищує допустиме [τ] більше ніж
на 5% (τ max > 1,05[τ]), то необхідно збільшити розміри перерізу
(№ двотавра) та виконати перевірку для нового перерізу.
Побудова епюр нормальних та дотичних напружень в небезпечному
поперечному перерізі та повна перевірка міцності двотаврової балки
Небезпечний переріз знаходиться в т. С, де
Q(x) = 30 кН , M(x) = 60 кН⋅м
Знайдемо значення нормальних та дотичних напружень для
характерних точок двотаврового перерізу (рис. 6.14), використовуючи
відомі формули
m прямок
=
121
122.
σ=Mz
y,
Iz
τ=
147,3
0
2
h
.
τ , МПа
0 0,5
16,3
136,1
20,8
0
4
h
I zb
σ , МПа
y
1
3
QyS z ( y )
z
d
136,1
t
0
0
0,5
16,3
t
b
147
Рисунок 6.14
Точка 1 належить граничній поверхні полиці “зверху”
у1 = h/2 = 0,135 м, S z ( y1 ) = 0, b = 0,135 м.
Mz
60 ⋅10 3
6
σ1 =
0
,
135
=
147,3⋅10
Па = 147,3 МПа,
y1 =
Iz
5500 ⋅10 −8
τ1 =
Q y S z ( y1 )
= 0 МПа.
I zb
Точка 2 належить полиці “знизу”
h
у2 = − t = 0,135 – 0,0102 = 0,1248 м, b = 0,135 м,
2
h t
0,27 0,0102
-6
3
S z ( y 2 ) = b ⋅ t − = 0,135 ⋅ 0,0102
−
= 178,9⋅10 (м ).
2
2 2
2
σ2 =
Mz
60 ⋅103
y2 =
0,1248 = 136,1 МПа,
−8
Iz
5500 ⋅10
τ2 =
Q y S z ( y2 )
τ3 =
Q y S z ( y3 )
30 ⋅103 ⋅178.9 ⋅10 −6
=
= 0,50 МПа.
I zb
5500 ⋅10 −8 ⋅135 ⋅10 −3
Точка 3 належить стінці в місті переходу стінки до полиці
у3 = у2 = 0,1248 м, S z ( y 3 ) = S z ( y 2 ) = 178,9⋅10-6 (м3), b = d = 0,006 м.
σ 3 = σ 2 = 136,1 МПа,
=
30 ⋅103 ⋅178.9 ⋅10 −6
Izb
5500 ⋅10 −8 ⋅ 6 ⋅10 −3
Точка 4 належить нейтральній лінії
122
= 16,3 МПа.
123.
у4 = 0 м, S z ( y 4 ) = S z max = 229 см3, b = d = 0,006 м.σ 4 = 0 МПа,
τ4 =
Q y S z max
=
30 ⋅103 ⋅ 229 ⋅10 −6
−8
−3
= 20,8 ⋅10 6 МПа.
Izb
5500 ⋅10 ⋅ 6 ⋅10
За отриманими значеннями нормальних та дотичних напружень
будуємо відповідні епюри в перерізі (рис. 6.14), враховуючи розташування
стиснутих волокон зверху (нормальні напруження в цьому місці будуть
мати знак “–”), а також симметричність обох епюр відносно нейтральної
лінії (осі z).
Еквівалентне напруження за третьою теорією міцності
2
2
III
σ екв
= σ x + 4 ⋅ τ xy .
III
Максимальне еквівалентне напруження σ екв
max буде спостерігатись
в точці 3 (за наявності досить великих дотичних напружень), тому
2
2
2
2
III
σ екв
max = σ 3 + 4 ⋅ τ 3 = 136.1 + 4 ⋅16.3 = 139,9 МПа < [σ] =160 МПа.
Умова міцності для точки “3” за третьою теорією міцності (для
пластичних матеріалів) також виконується.
Вказівка. При невиконанні умови міцності.
III
Якщо максимальне еквівалентне напруження σ екв
не
max
III
перевищує допустиме [σ] більше ніж на 5% ( σ екв
max < 1,05[σ]), то
розміри перерізу (№ двотавра) залишають без змін з відповідним
III
обґрунтуванням. Якщо σ екв
max перевищує допустиме [σ] більше
III
ніж на 5% ( σ екв
max > 1,05[σ]), то необхідно збільшити № двотавра
та виконати перевірку для нового перерізу тільки в точці 3.
Розрахунок балки на жорсткість
Рівняння кутів повороту і прогинів для балки (див. рис. 6.13 а) за
методом початкових параметрів (див. рівняння 6.25, 6.26, рис. 6.8)
R A ( x − 2 )2 q (x − 4 )3 q (x − 6 )3 F (x − 6 )2
1
θ = θ0 +
−
+
−
,
Mx +
EI z
2
6
6
2
2
R A ( x − 2 )3 q (x − 4 )4 q (x − 6 )4 F (x − 6 )3
1 M (x )
y = y0 + θ 0 x +
+
−
+
−
.
EI z 2
6
24
24
6
Ділянка ЕА
0 м ≤ х ≤ 2 м.
1 M (x )2
y( x ) = y0 + θ 0x +
.
EI z
2
(6.28)
Ділянка AD
123
124.
2 м ≤ х ≤ 4 м.2
R A ( x − 2 )3
1 M (x )
y( x ) = y0 + θ 0 x +
+
,
EI z 2
6
(6.29)
Ділянка BC
4 м ≤ х ≤ 6 м.
2
R A ( x − 2 )3 q (x − 4 )4
1 M (x )
y( x ) = y0 + θ 0 x +
−
+
.
EI z 2
6
24
(6.30)
Ділянка CD
6 м ≤ х ≤ 8 м.
1 M (x )2 R A ( x − 2 )3 q(x − 4 )4 q(x − 6)4 F (x − 6)3
y( x ) = y0 + θ 0 x +
+
−
+
−
.
EI z 2
6
24
24
6
Початкові параметри у0 та θ0 визначимо із умов закріплення балки
при х = 2 м , y(2) = 0;
при х = 8 м , y(8) = 0.
103 40⋅ 82 10(8 − 2)3 10(8 − 4)4 10(8 − 6)4 20(8 − 6)3
y(8) = y0 + 8θ0 +
+
−
+
−
= 0;
EI z 2
6
24
24
6
103 40 ⋅ 2 2
y(2 ) = y0 + 2θ 0 +
= 0,
EI z 2
1513⋅103
y0 + 8θ 0 +
=0;
EI z
80 ⋅103
y0 + 2θ 0 +
=0.
EI z
Розв’язок системи рівнянь
− 239 ⋅10 3
− 239 ⋅10 3
= -0,021 (рад),
θ0 =
=
EI z
2,1 ⋅1011 ⋅ 5500 ⋅10 −8
398 ⋅10 3
398 ⋅10 3
= 0,034 (м).
y0 =
=
EI z
2,1 ⋅1011 ⋅ 5500 ⋅10 −8
Вказівка. В загальному вигляді система типових рівнянь має розв’язок
α
1 β −α
;
=0;
θ0 =
y0 + x1θ 0 +
EI z
EI z x1 − x 2
y0 + x 2θ 0 +
β
EI z
= 0.
y0 =
1 α ⋅ x 2 − β ⋅ x1
.
EI z
x1 − x 2
Кінцеве загальне рівняння пружної лінії та кутів повороту перерізу
124
125.
y( x ) = 0,034 − 0,021x +103
2,1⋅1011 ⋅ 5500⋅10−8
×
40 ⋅ x 2 10( x − 2 )3 10(x − 4)4 10(x − 6)4 20(x − 6)3
×
+
−
+
−
,
6
24
24
6
2
θ ( x ) = −0,021+
103
2,1⋅1011 ⋅ 5500⋅10−8
×
3
3
2
10( x − 2 )2 10(x − 4) 10(x − 6) 20(x − 6)
× 40 ⋅ x +
−
+
−
.
2
6
6
2
Розраховані прогини та кути повороту перерізу для низки значень х
приведені в таблиці 6.2.
Вказівка. Для побудови пружної лінії необхідно обов’язково розрахувати
прогини посередині між точками опор та в крайніх точках
консольних ділянок, якщо такі є. З незначною похибкою можна
вважати, що в одній з цих точок прогин буде мати максимальне
значення. Для наочності графіка необхідно взяти також
проміжні точки з певним інтервалом (наприклад, 1 м).
Таблиця 6.2
х, м
0
1
2
3
4
5
6
7
8
у(х),
34
15
0
-12
-19
-22
-19
-11
0
мм
θ(х),
-0,021 -0,017 -0,014 -0,010 -0,005
0
0,006 0,010 0,011
рад
Знак “мінус” при у(х) та θ(х) вказує, що балка в цій точці
прогинається вниз, а переріз повертається вправо.
За отриманими значеннями будуємо відповідні графіки пружної лінії
та кутів повороту перерізу (див. рис. 6.13 г, д).
Підбираємо необхідний за умовою жорсткості переріз
Допустимий прогин
[f] = l/400 = 8/400 = 0,02 (м) = 20 мм.
Максимальний прогин (див табл. 6.2) за модулем уmax = 34 мм.
Умова жорсткості балки
уmax ≤ [f]
не виконується уmax = 34 мм > [f] = 20 мм, тому необхідно підібрати більш
жорсткий переріз (збільшити розміри або підвищити номер двотавра).
Необхідний мінімальний момент інерції перерізу має бути
y
34
I z min = I z max = 5500
= 9350 (см4) .
[f ]
20
За сортаментом підбираємо двотавр №33, в якого I z = 9840 (см4).
125
126.
В додатку Г приведена програма-інструкція розрахунку на міцністьта жорсткість двоопорних балок. Контроль машинного розрахунку та
вручну виконується на всіх етапах розв’язування задачі.
ЛІТЕРАТУРА
1. Огородніков В.А., Сивак І.О., Бабак М.В. Опір матеріалів з елементами
теорії пластичності. Частина 1. Навчальний посібник. — Вінниця:
ВДТУ, 2001 — 100 с.
2. Писарененко Г.С., Квітка О.Л., Уманський Е.С. Опір матеріалів. –К.:
Вища школа, 1995.
3. Нахайчук В.Г., Матвійчук В.А., Чернілевський О.В. Технічна механіка.
Кн. 2. Опір матеріалів. − К.: НМКВО, 1992 р.
5. Сборник задач по сопротивлению материалов. / Под ред. Качурина В.К.
М., 1972.
6. Сборник задач по сопротивлению материалов / Уманский А.А.,
Афанасьев А.М., Вольмир А.С. и др. М., 1973.
7. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М., 1975.
8. Феодосьев В.И. Сопротивление материалов: Учебник для втузов. — М.:
Наука, 1986. — 512 с.
10.Сопротивление материалов: Учебник для вузов / под общ. ред. Г.С.
Писаренко. — Киев: Вища школа, 1979 — 696 с.
11. Н.М. Беляев. Сопротивление материалов. — М.: Наука, 1976 — 608 с.
12. Справочник по сопротивлению материалов / Е.Ф. Винокуров, М.К.
Балыкин, И.А. Голубев и др. — Мн.: Наука и техника, 1988 — 464 с.
13. Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по
сопротивлению материалов. — Киев: Наукова думка, 1975 — 704 с.
126





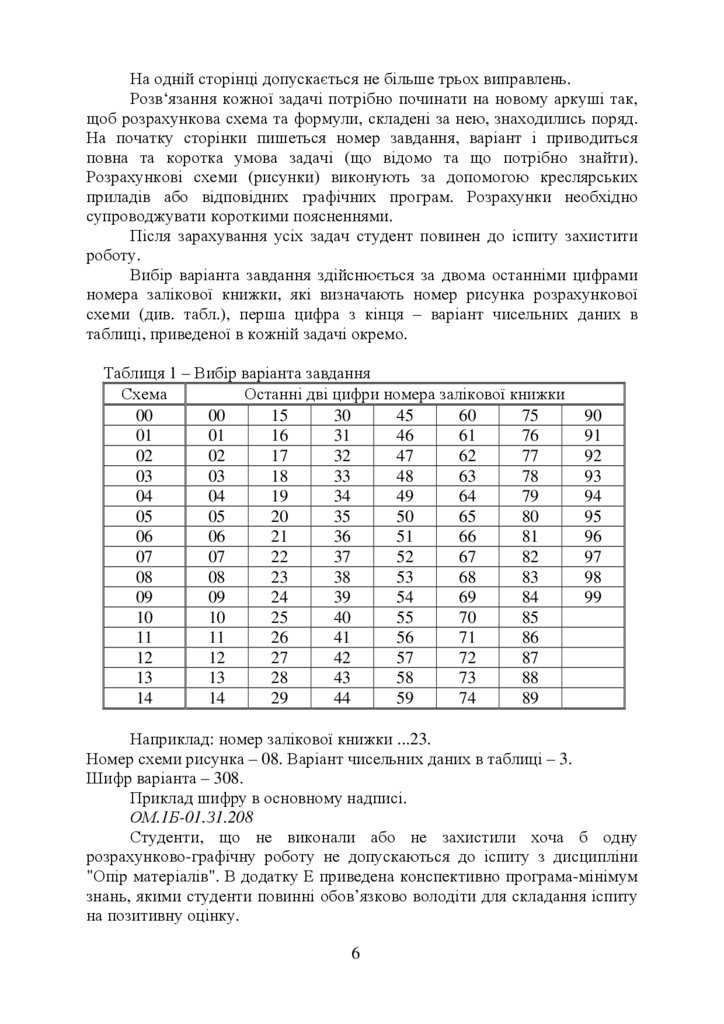



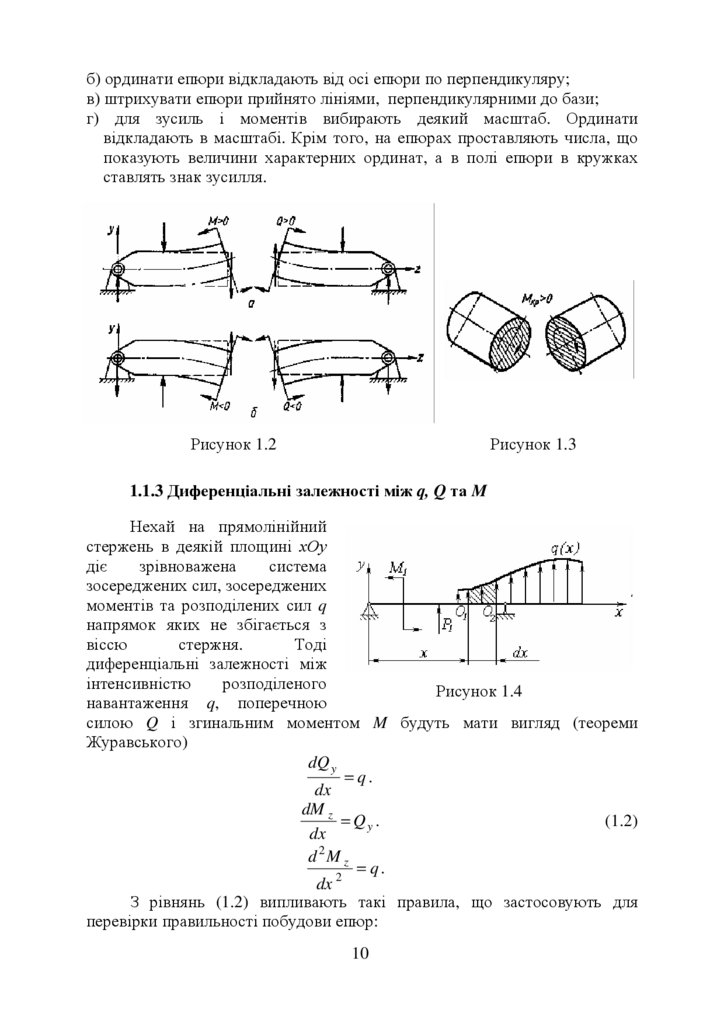


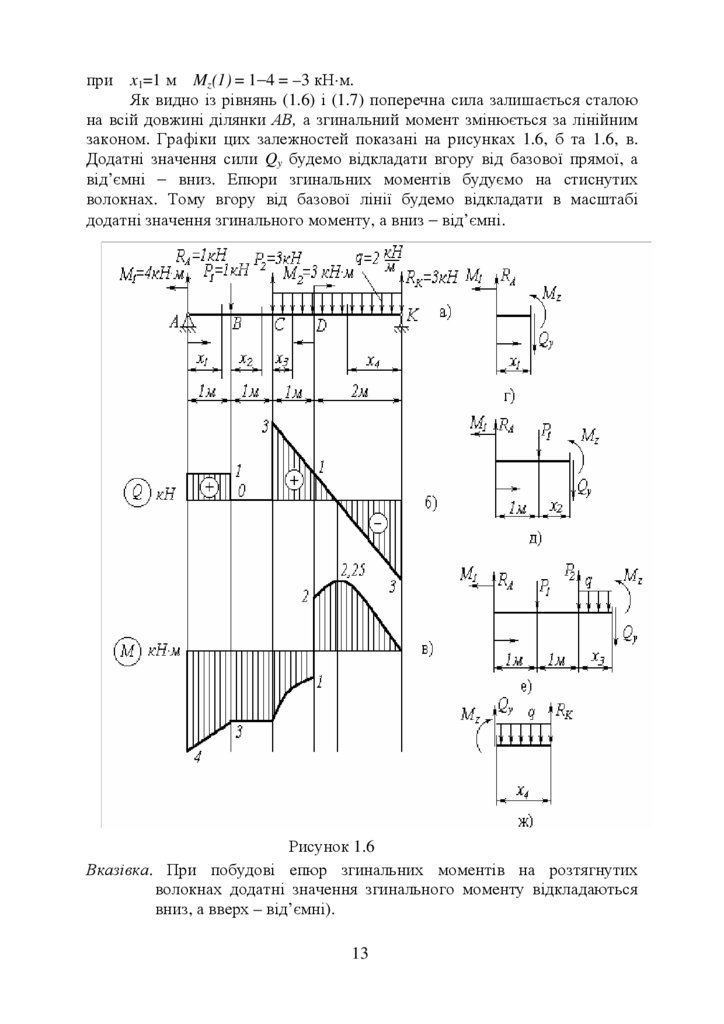


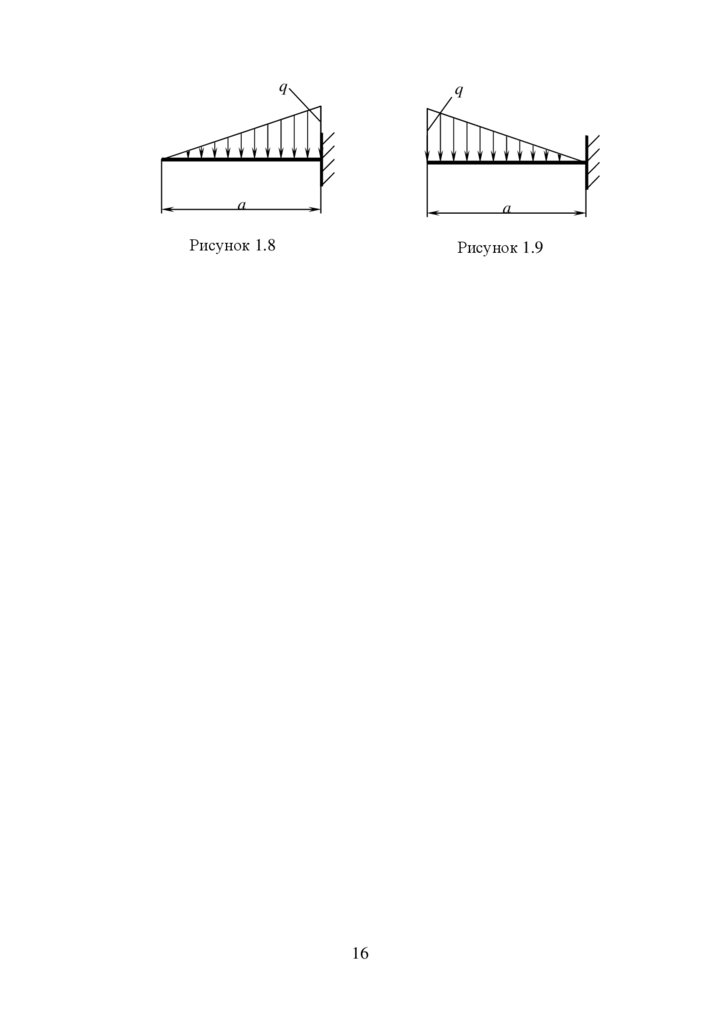


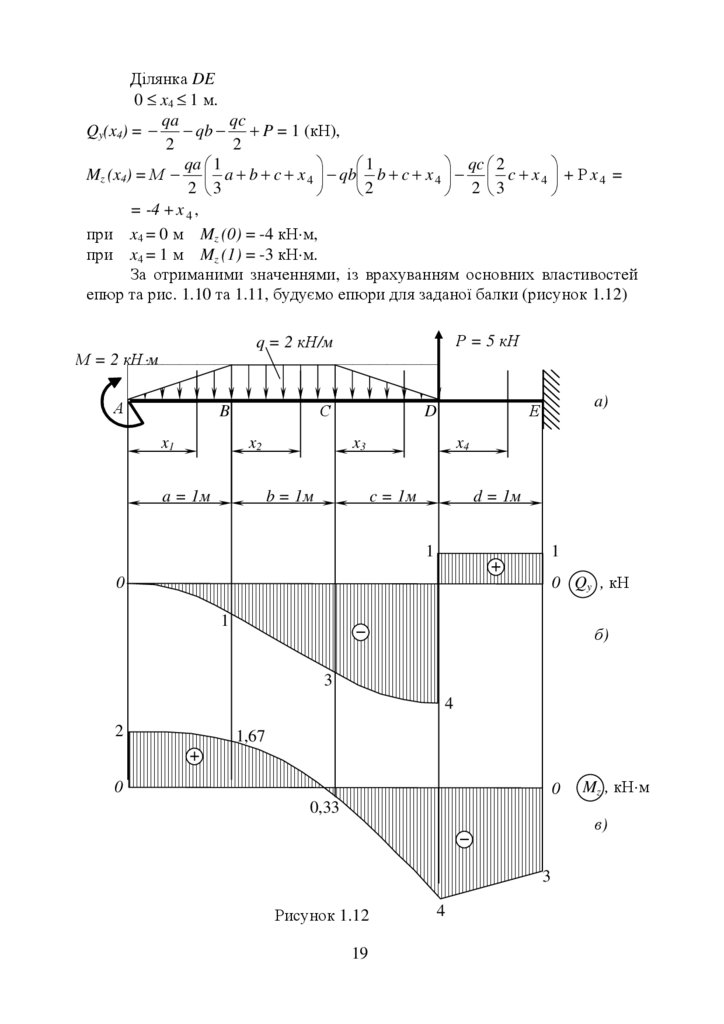







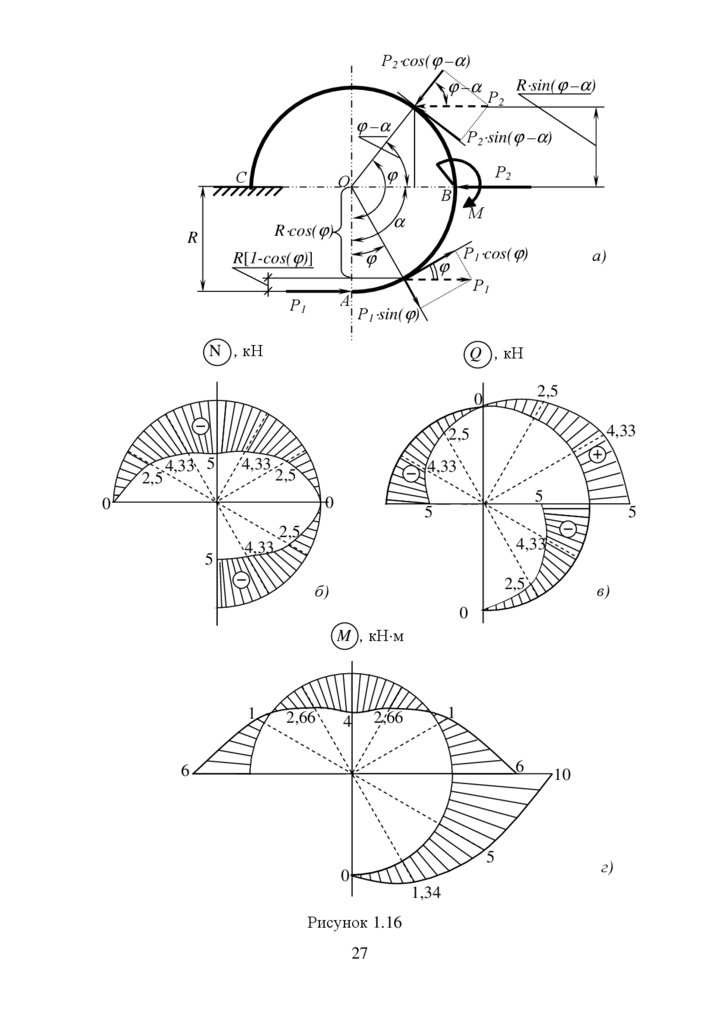





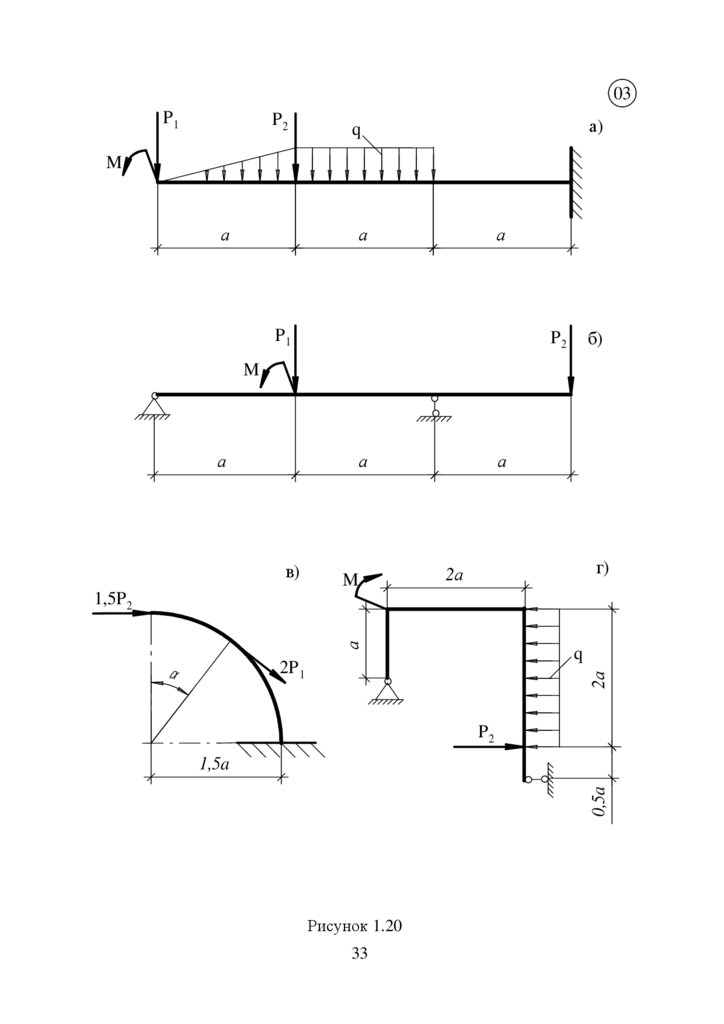
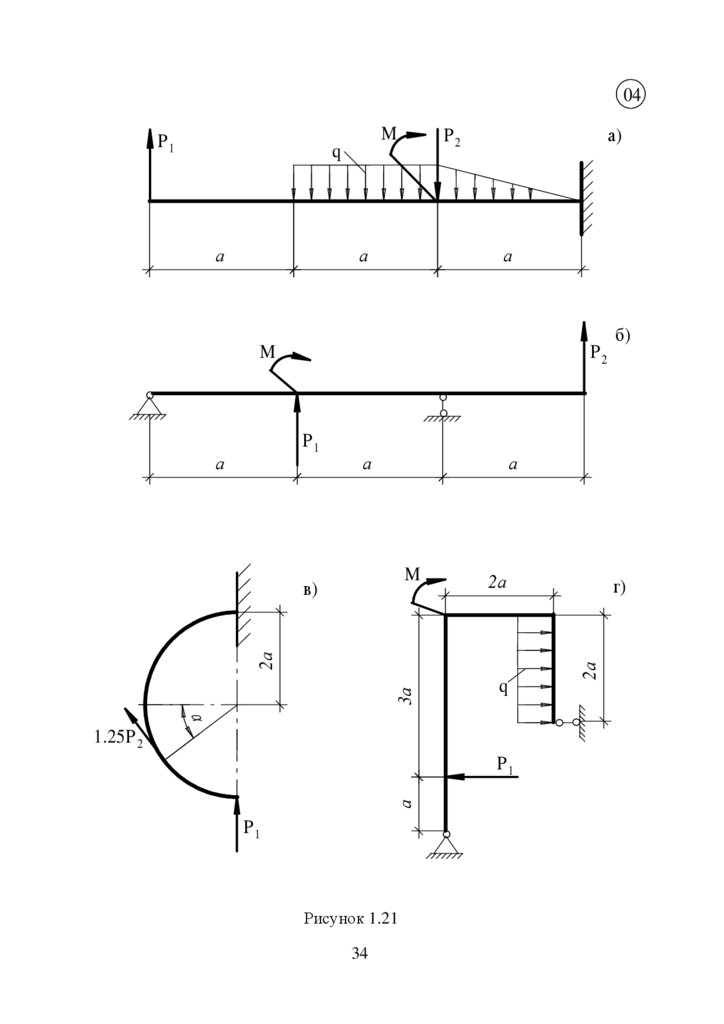
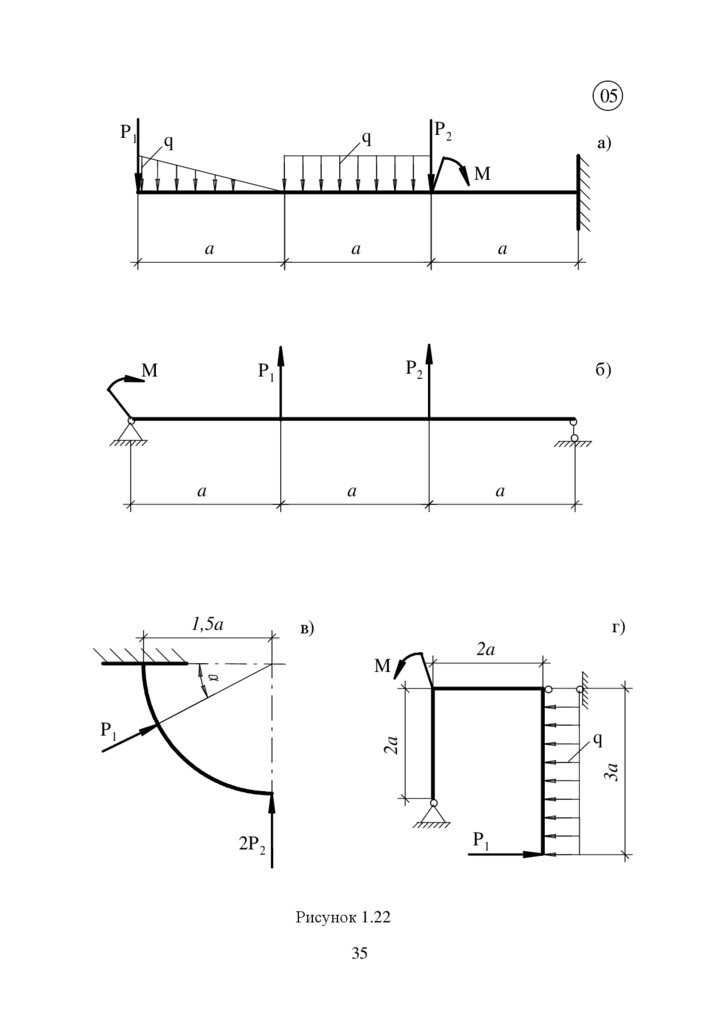
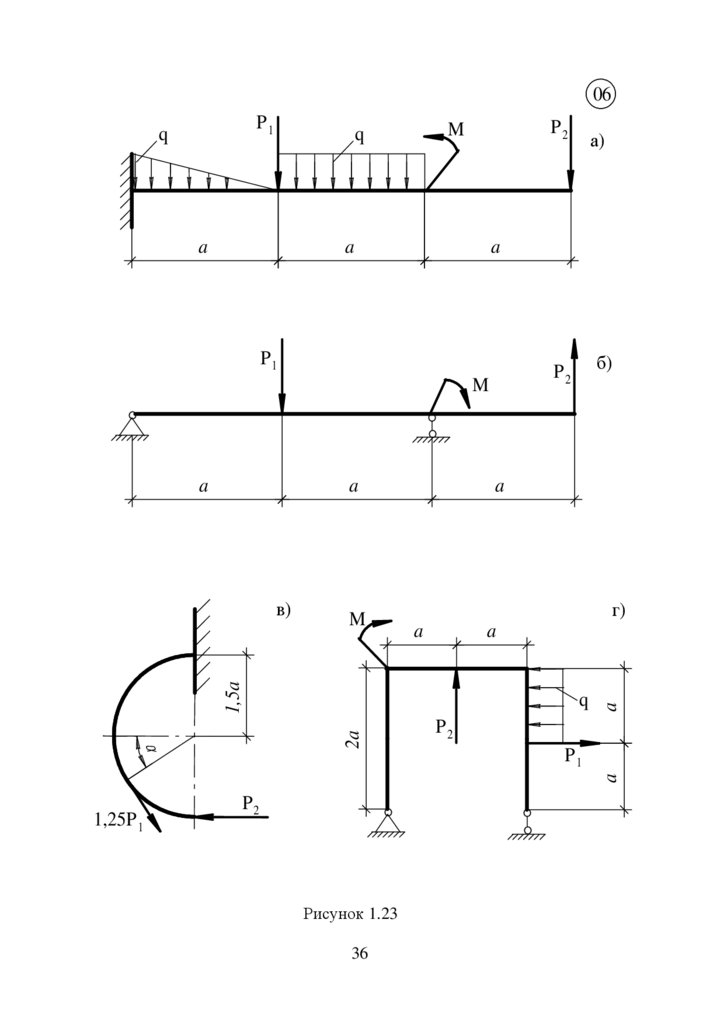

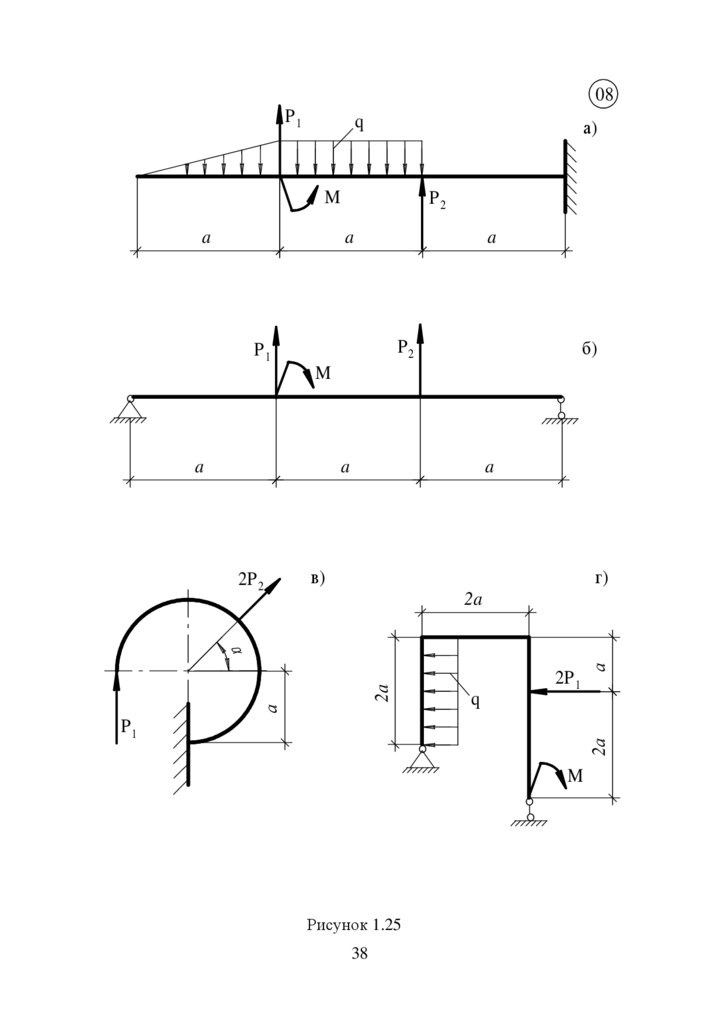
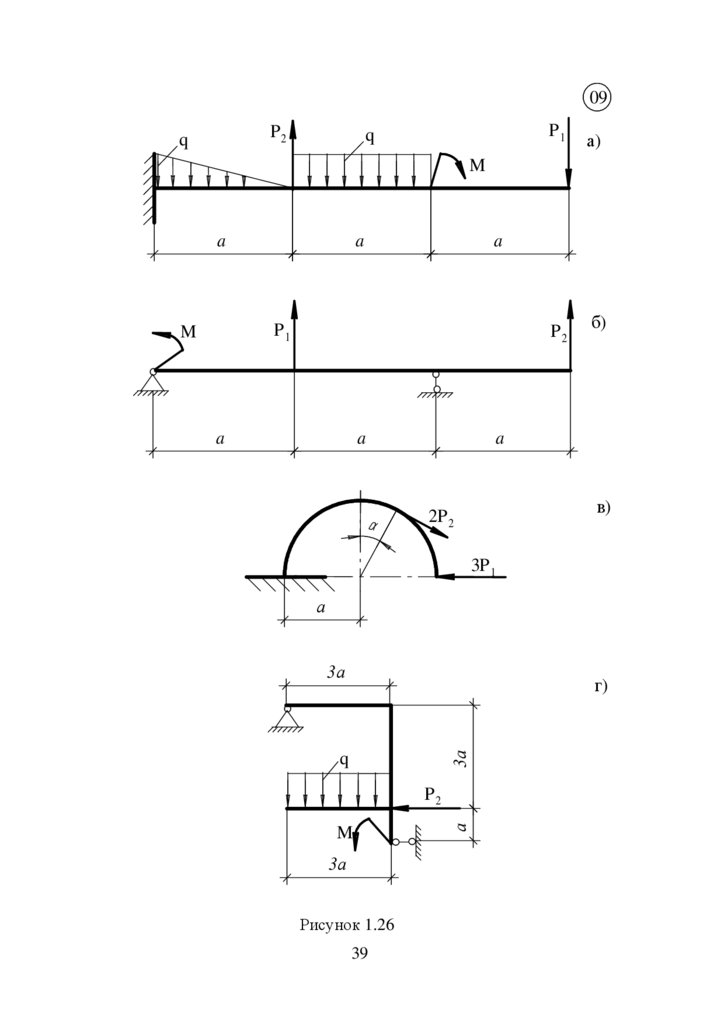
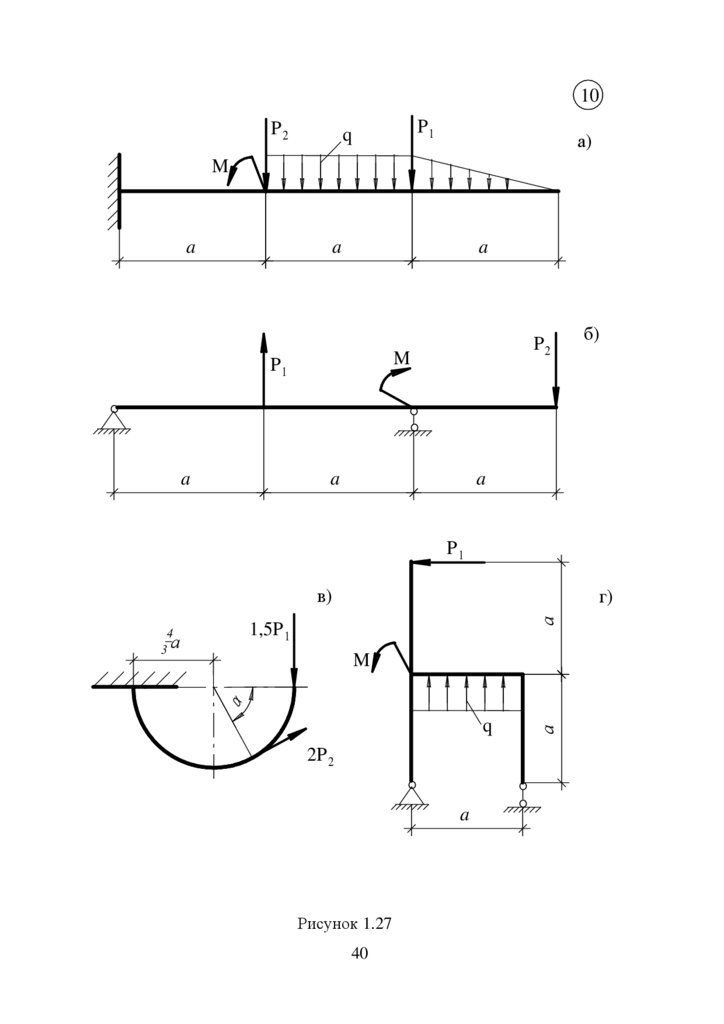

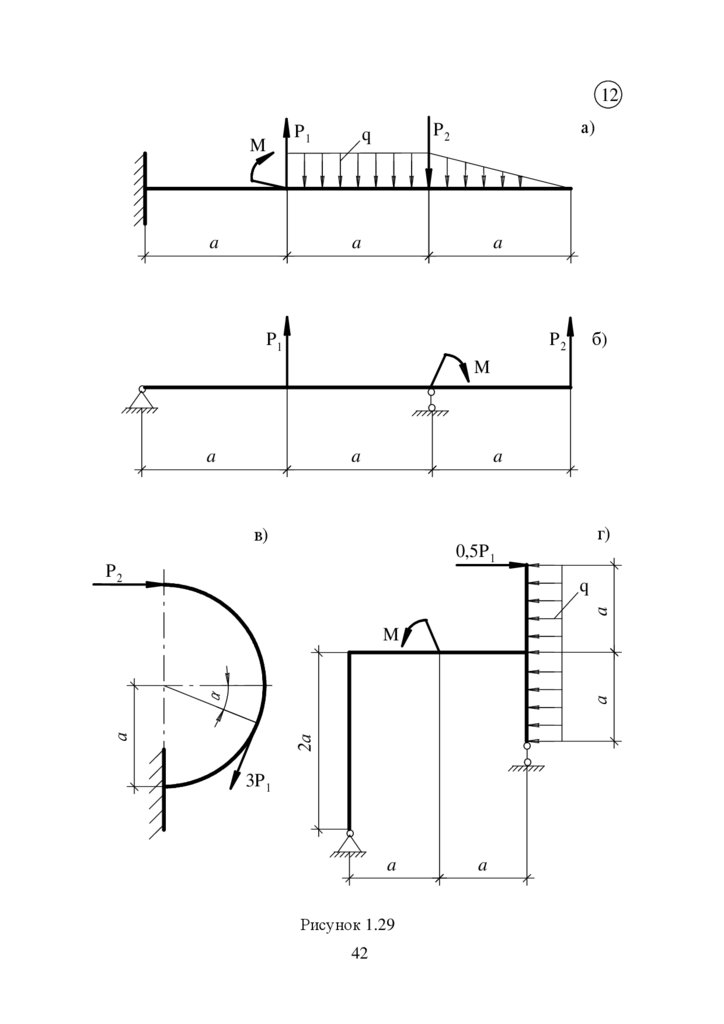
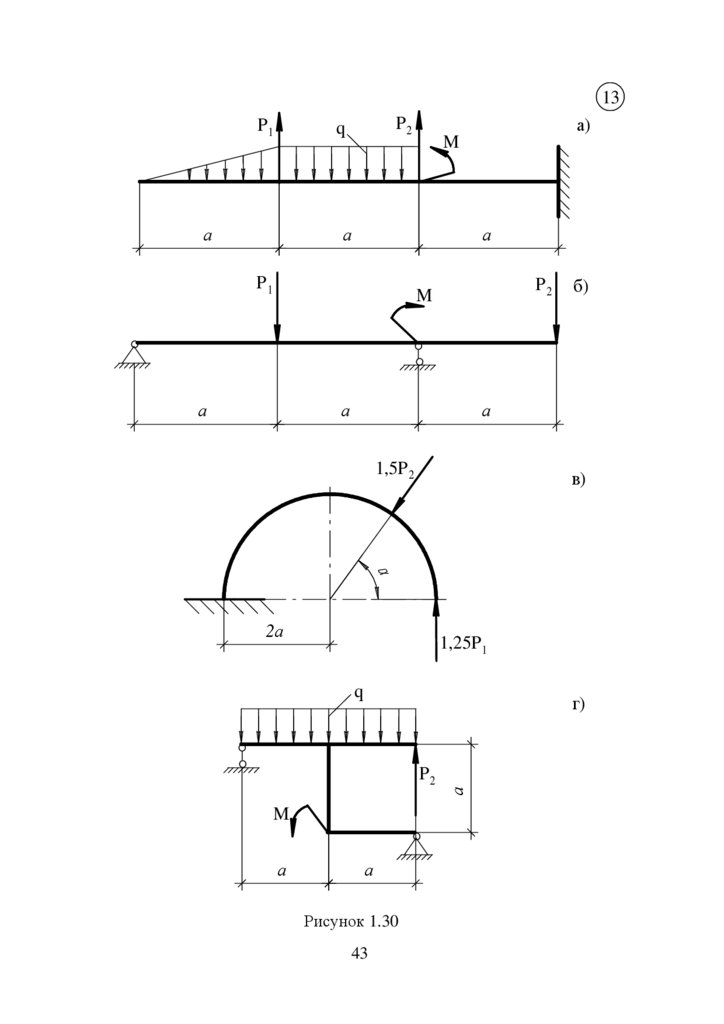
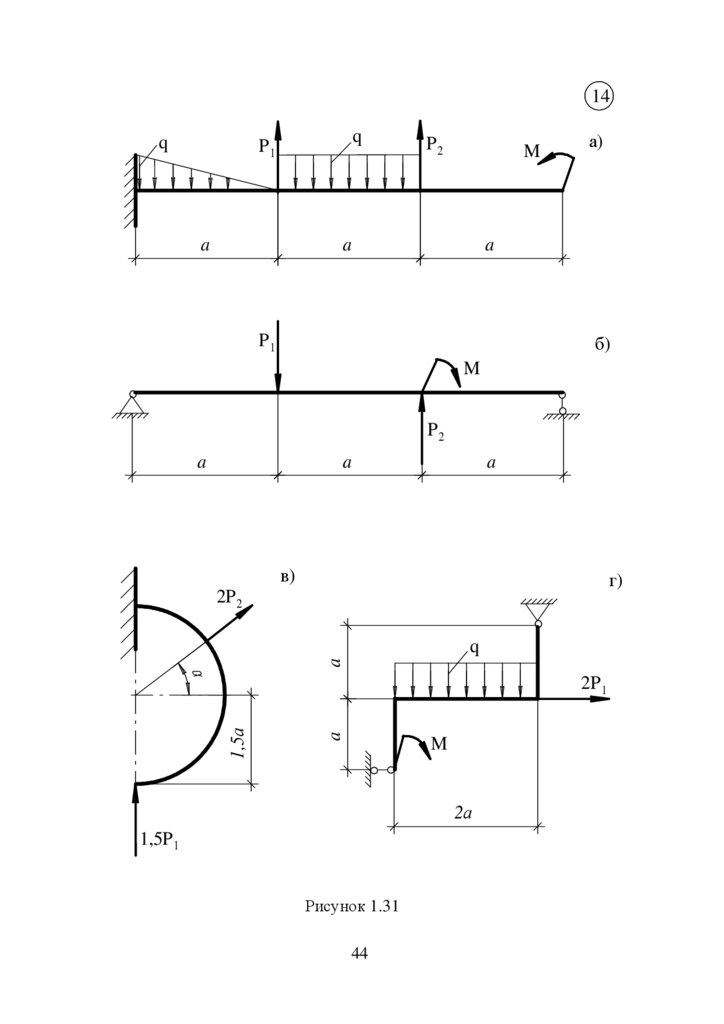





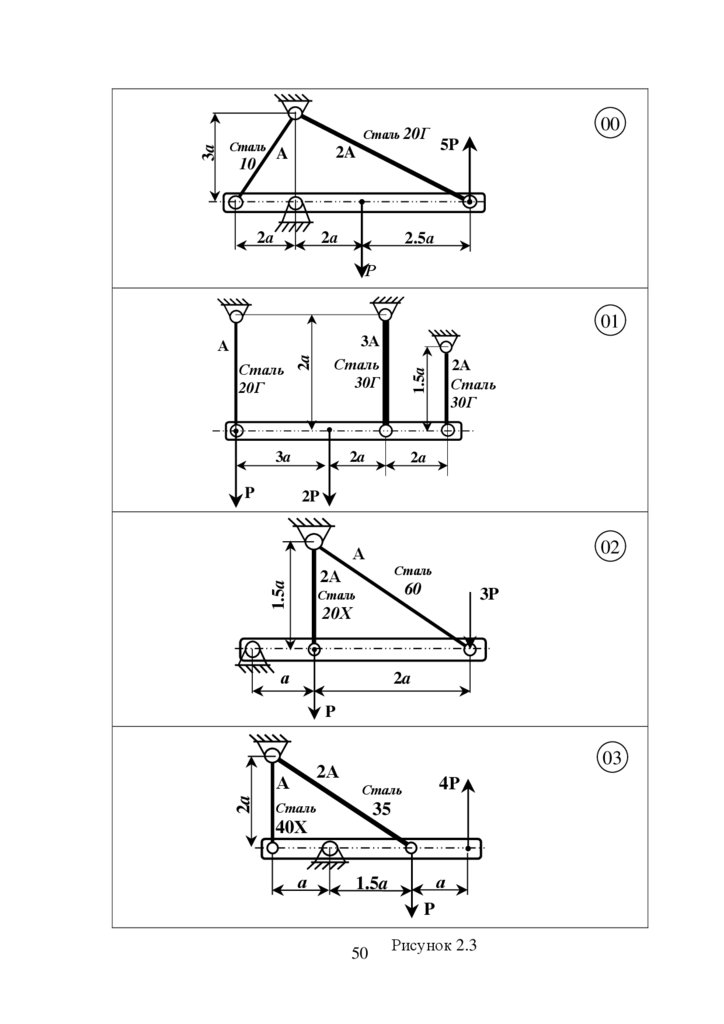

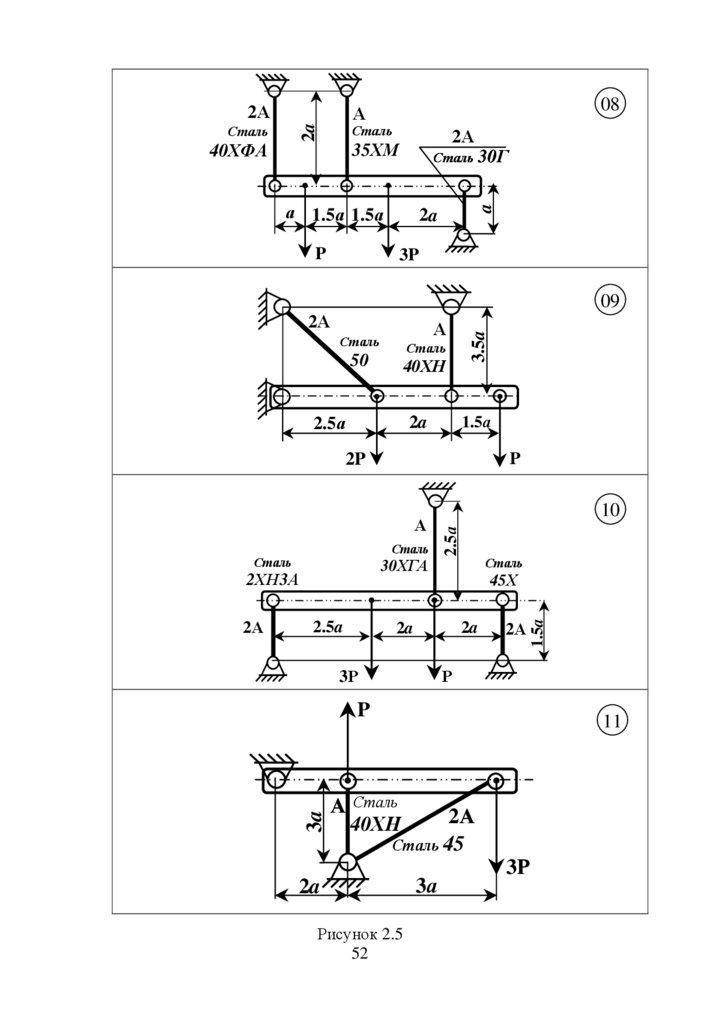
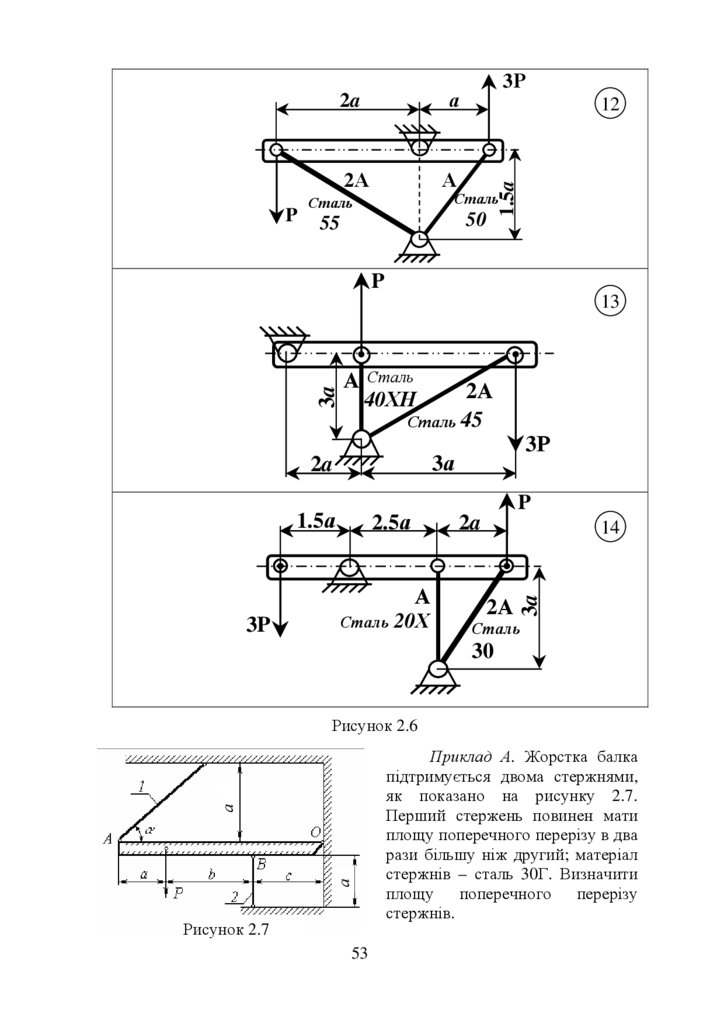









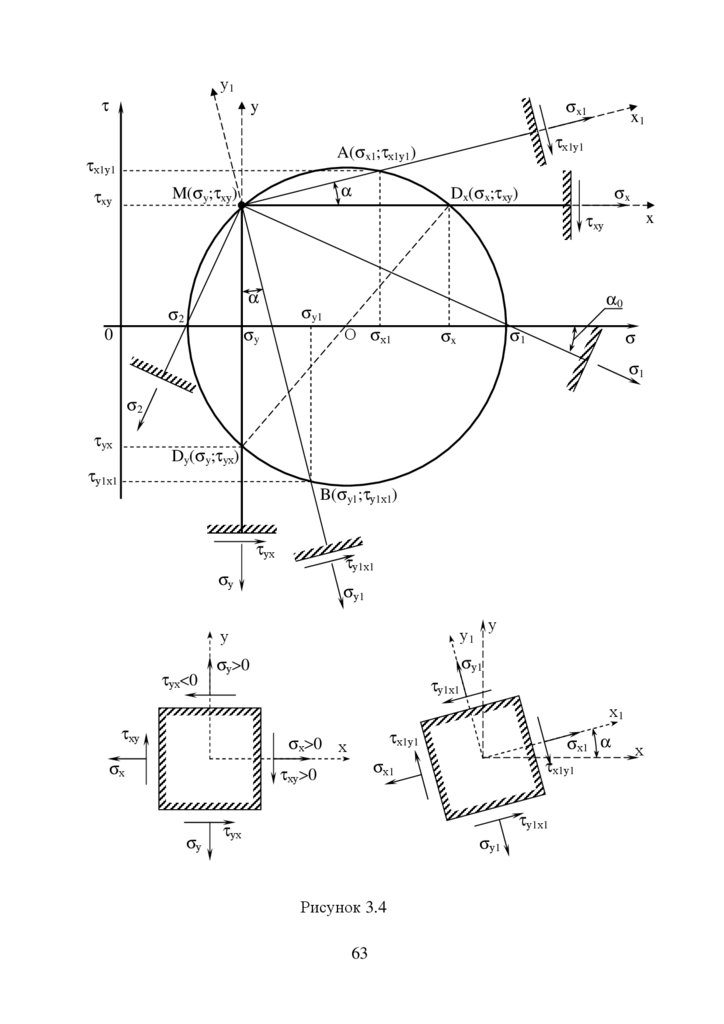





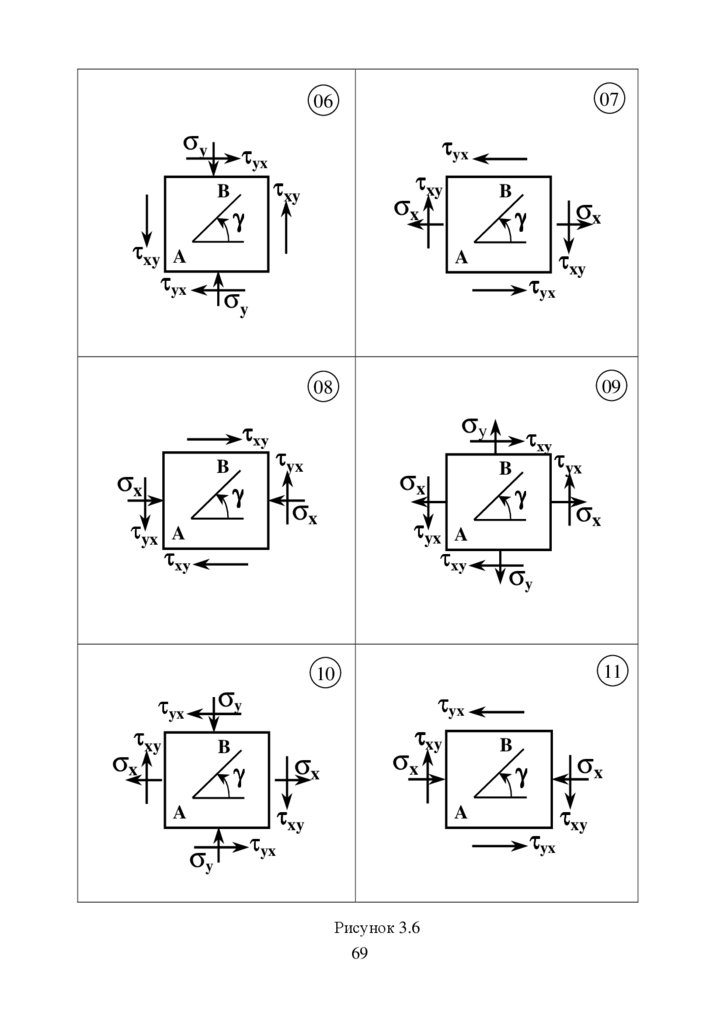
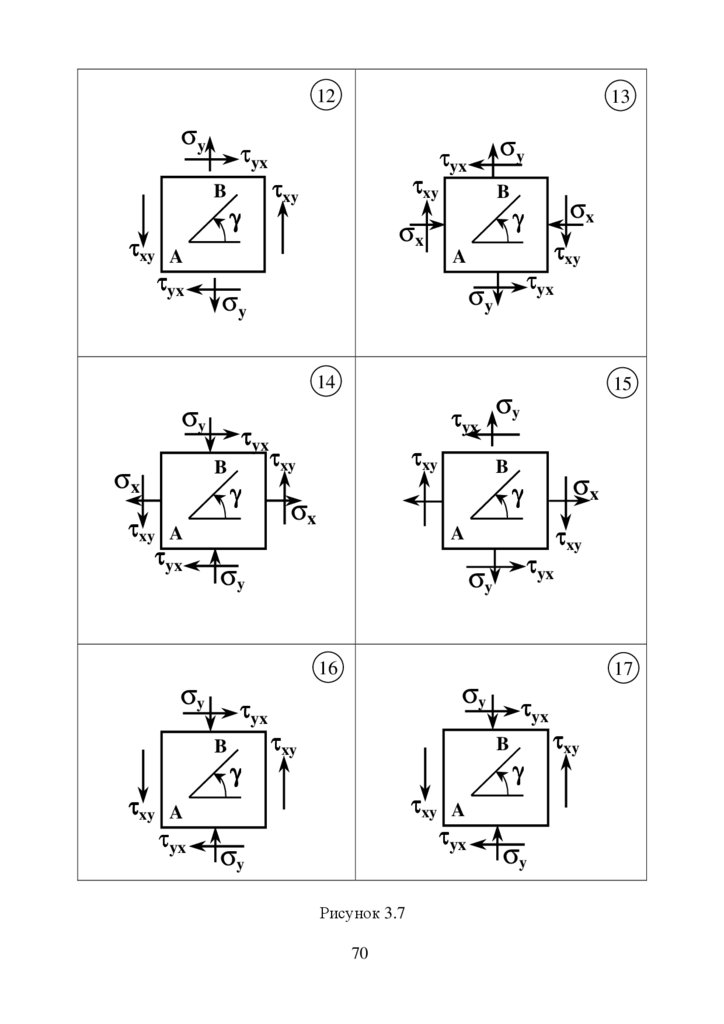











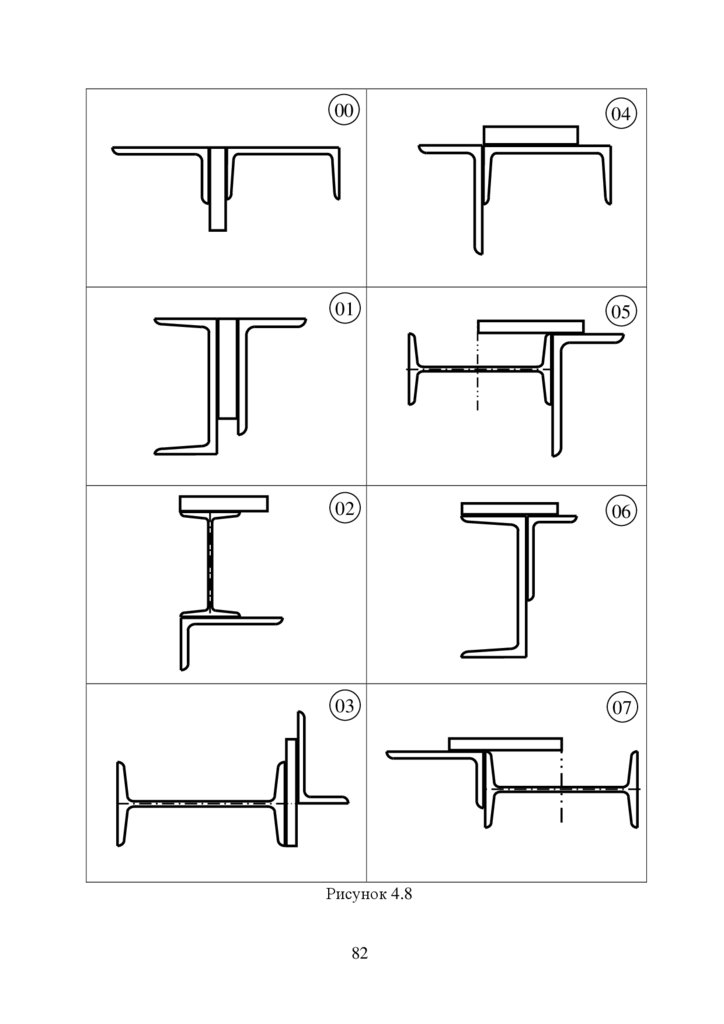
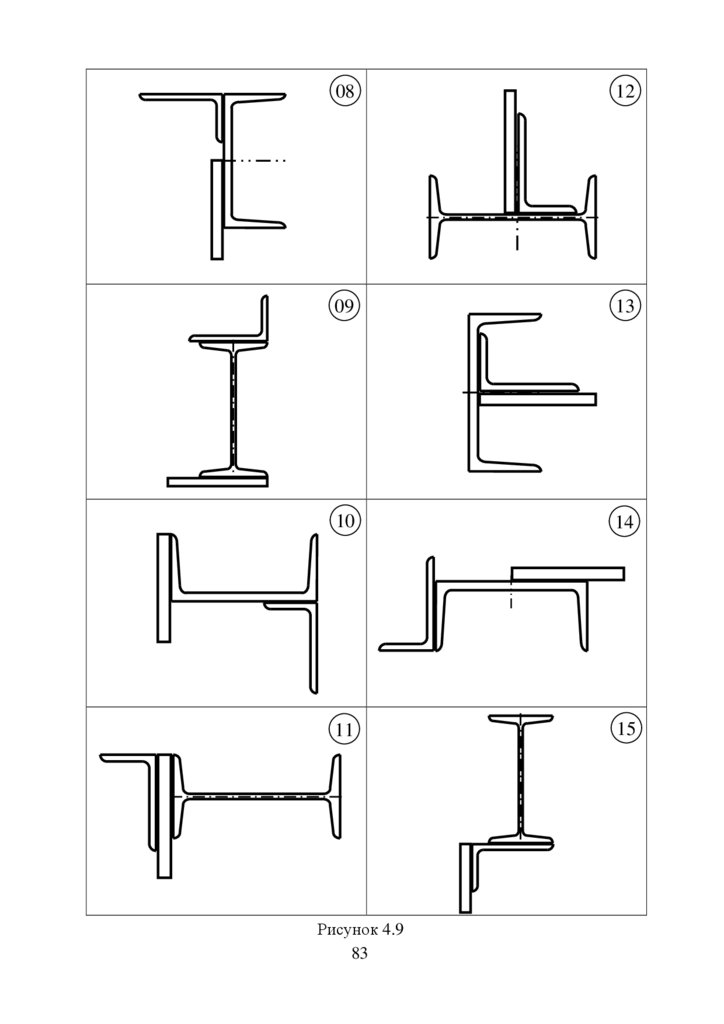

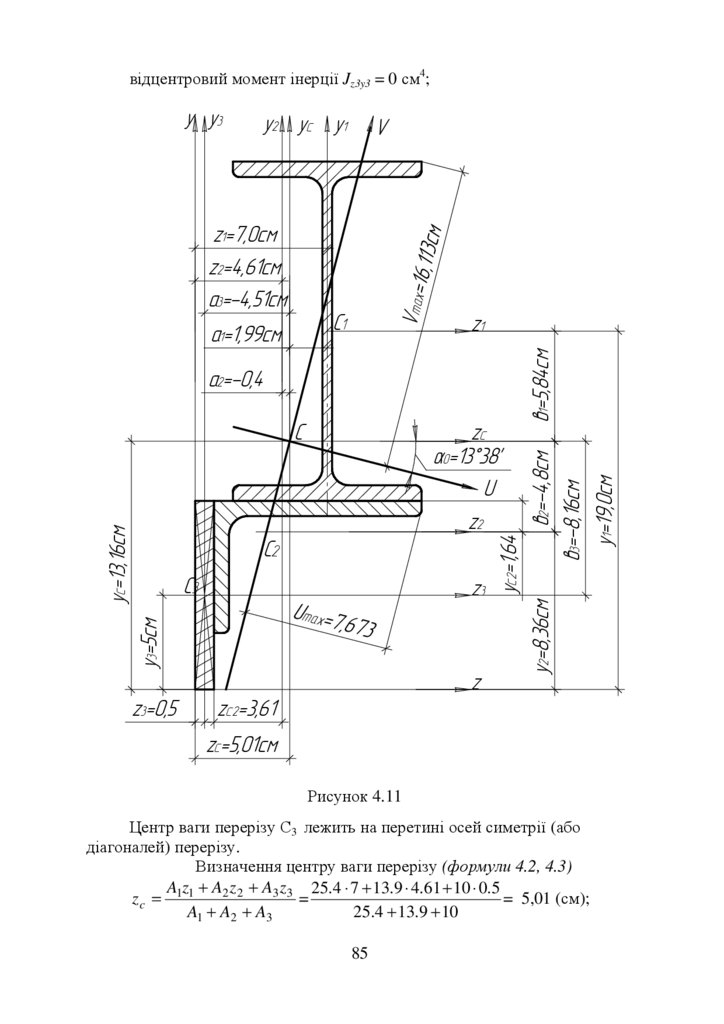








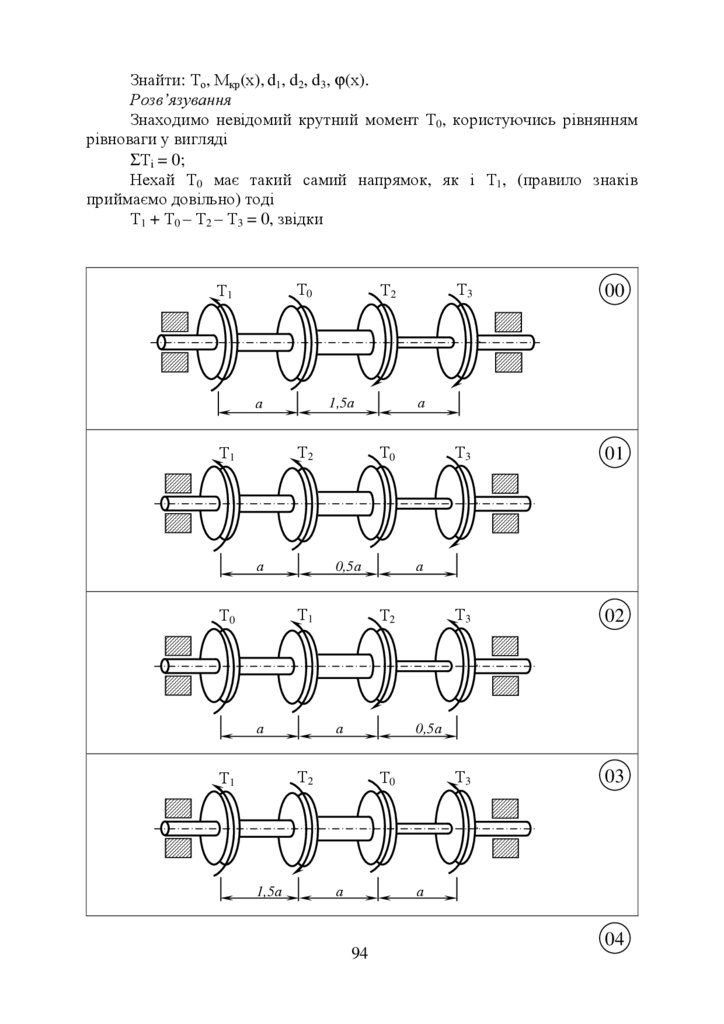

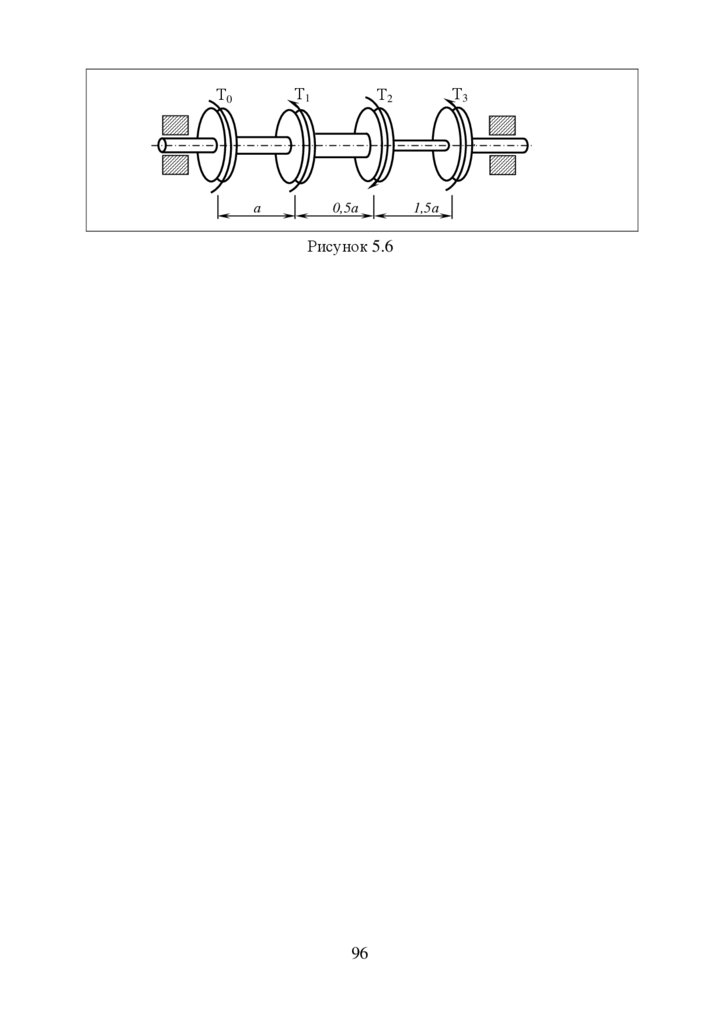


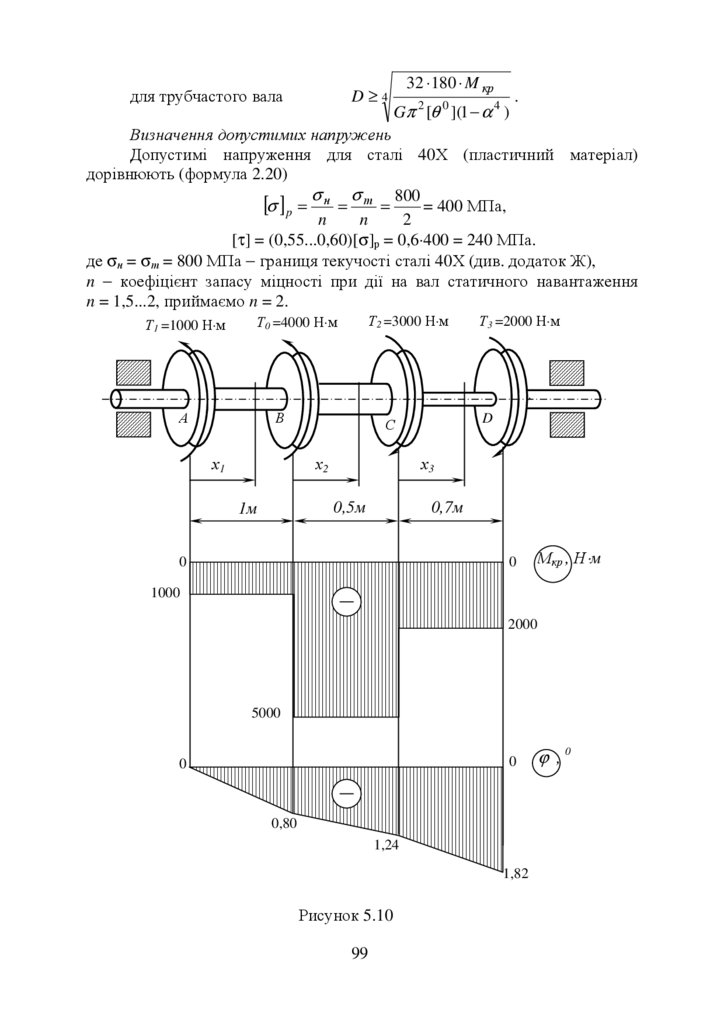













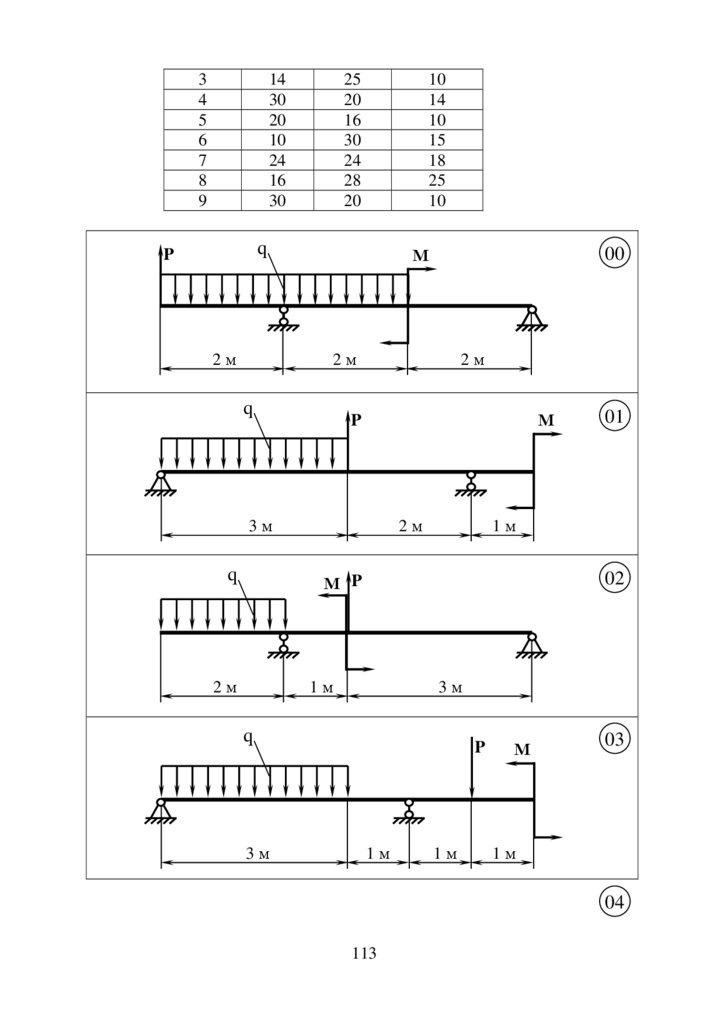

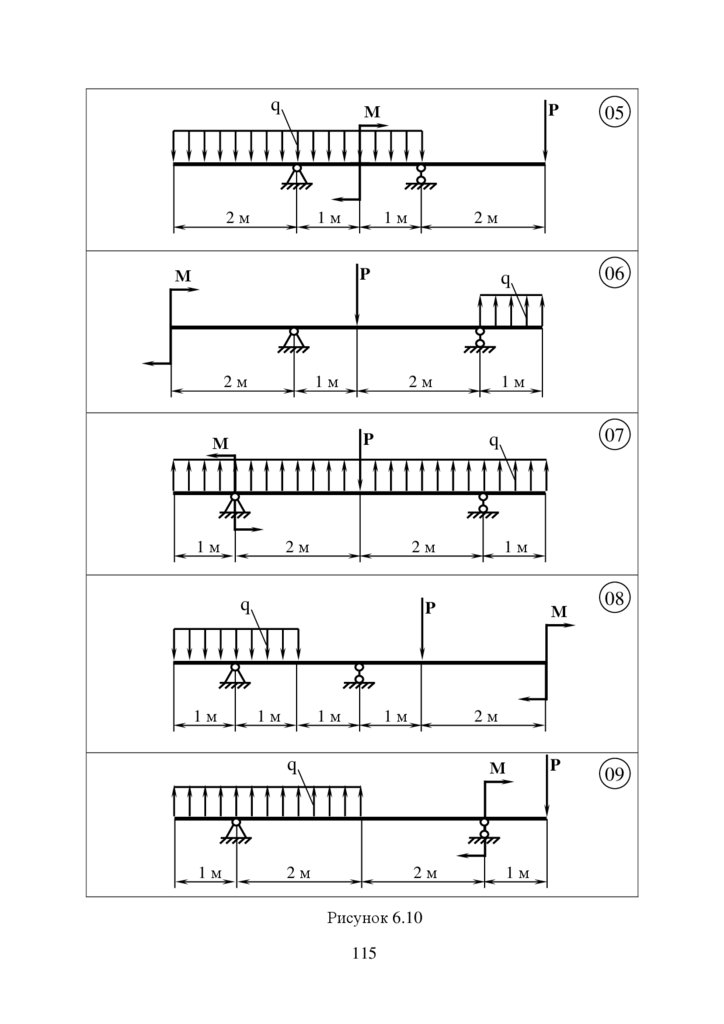


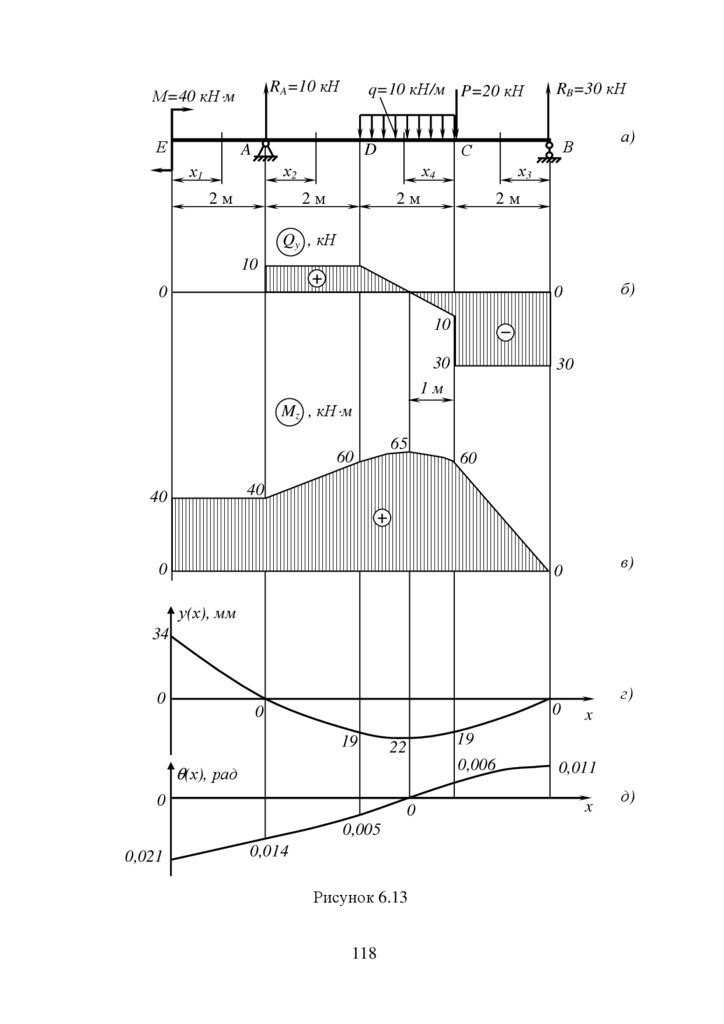



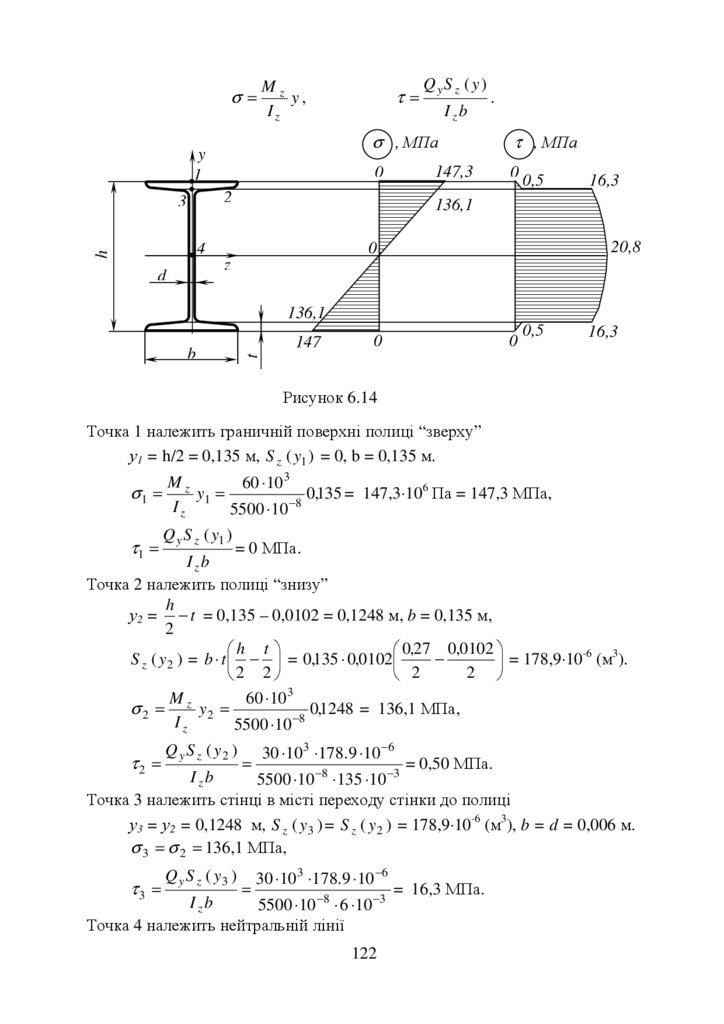




 physics
physics drafting
drafting








