Similar presentations:
Функция и способы ее задания. Преобразования графиков функций
1.
Тема урока:Функция и способы ее задания.
Преобразования графиков функций.
2.
Цель урока:10.4.1.1 - знать определение и способы
задания функции;
10.4.1.2 - уметь выполнять
преобразования графика функции
(параллельный перенос, сжатие и
растяжение)
3.
Функция – зависимость при которой, каждомузначению величины Х (аргумента) соответствует
единственное значение величины У (функции).
4.
5.
Определение:Функцией называют зависимость,
где каждому элементу х из множества определения
функции X ставят в соответствие единственный элемент
у из множества значений функции Y. Такую зависимость,
записывают в виде: у=f(х). Саму функцию, кроме буквы f
обозначают буквами t, s, v, u, φ, ψ, F и т.д. Где х называют
независимой переменной(или аргументом), а у называют
значением функции(или зависимой переменной).
6.
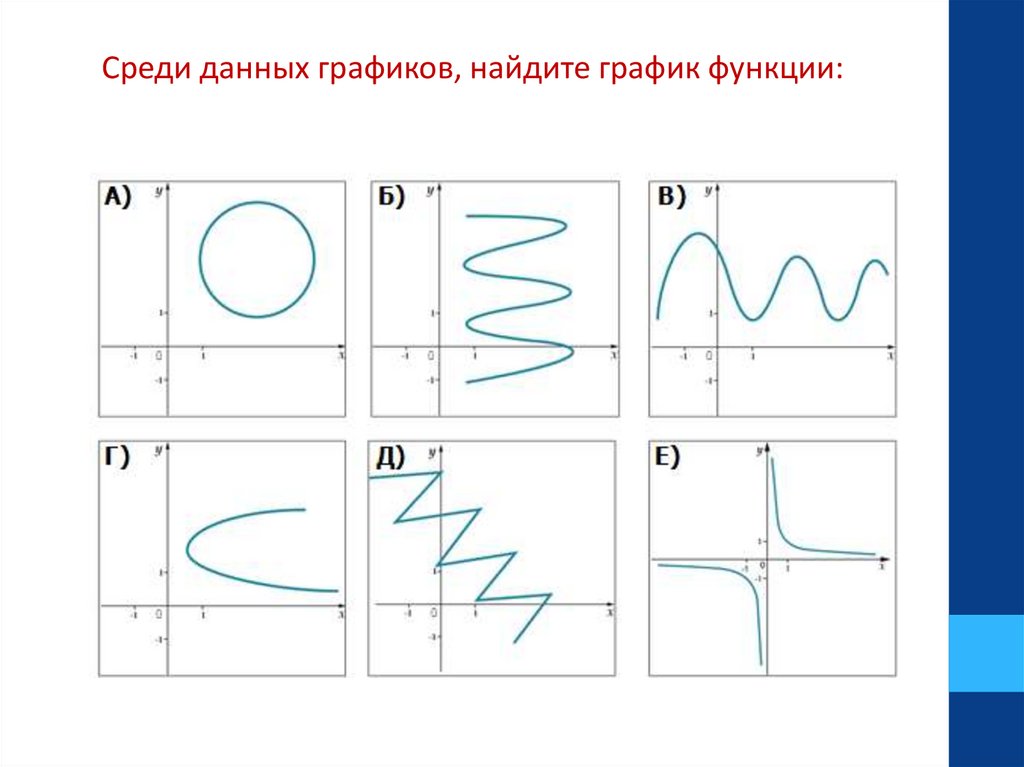
Среди данных графиков, найдите график функции:7.
8.
Способы задания функции1. АНАЛИТИЧЕСКИЙ
2. ГРАФИЧЕСКИЙ
3. ТАБЛИЧНЫЙ
4. СЛОВЕСНЫЙ
9.
Способы задания функции1. АНАЛИТИЧЕСКИЙ
функция задается при помощи формулы или нескольких
формул
Например,
у х 4 х 7,
2
у 2 x,
x 2 , если х 0,
f ( x)
х 3, если х 0.
10.
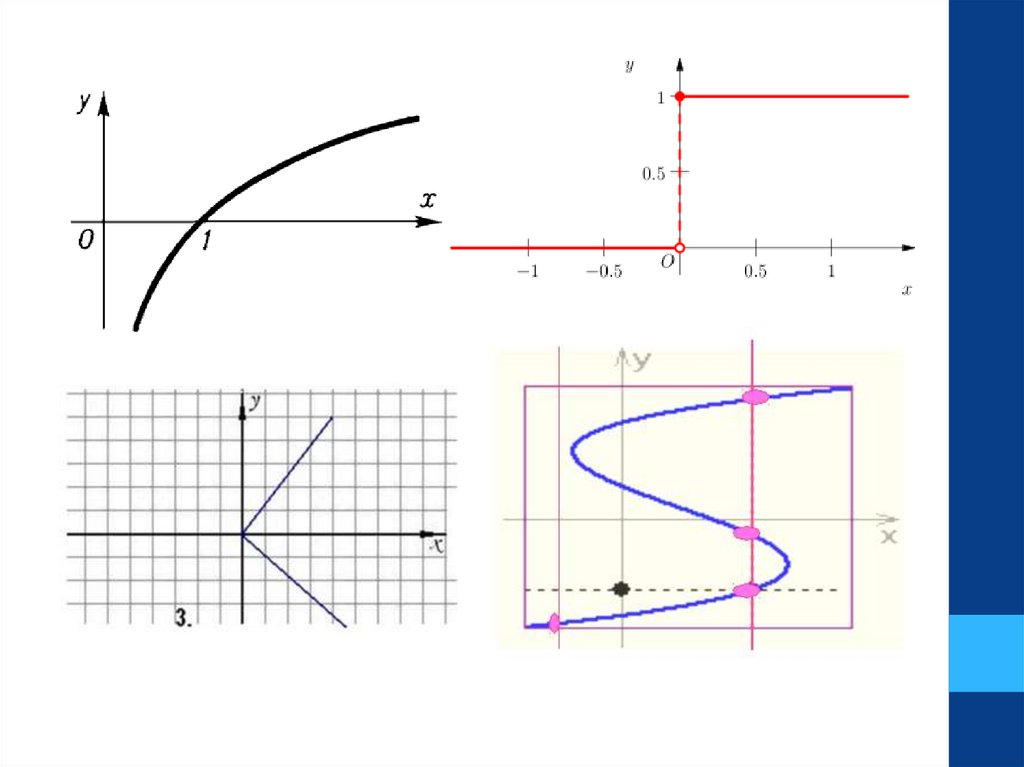
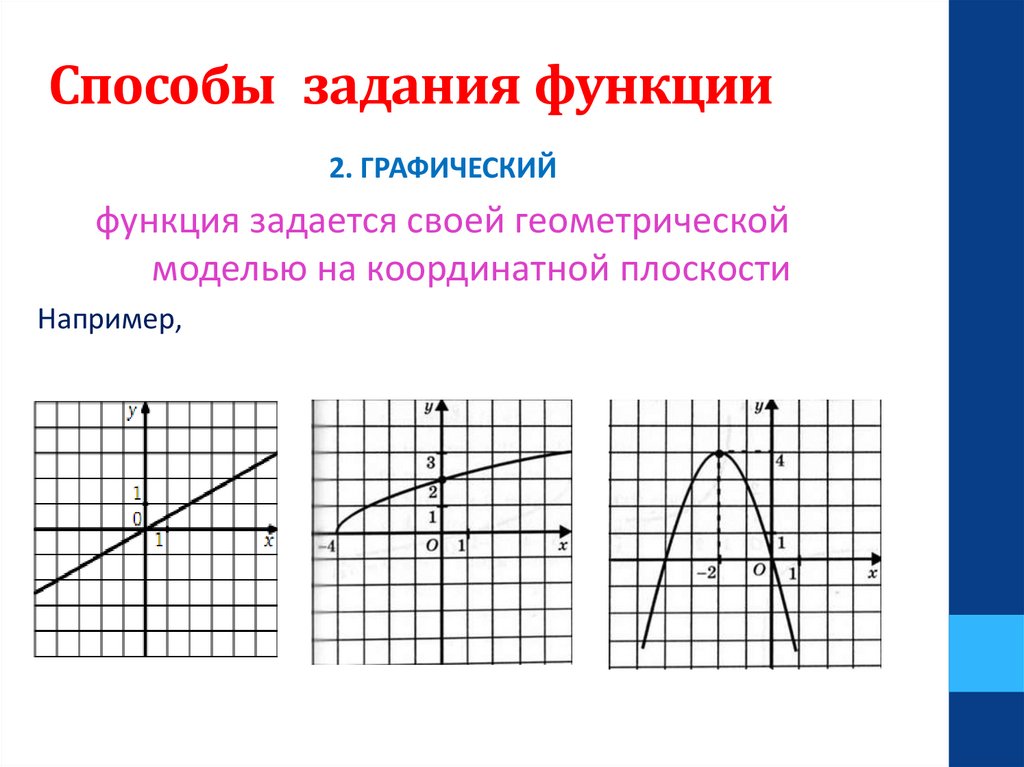
Способы задания функции2. ГРАФИЧЕСКИЙ
функция задается своей геометрической
моделью на координатной плоскости
Например,
11.
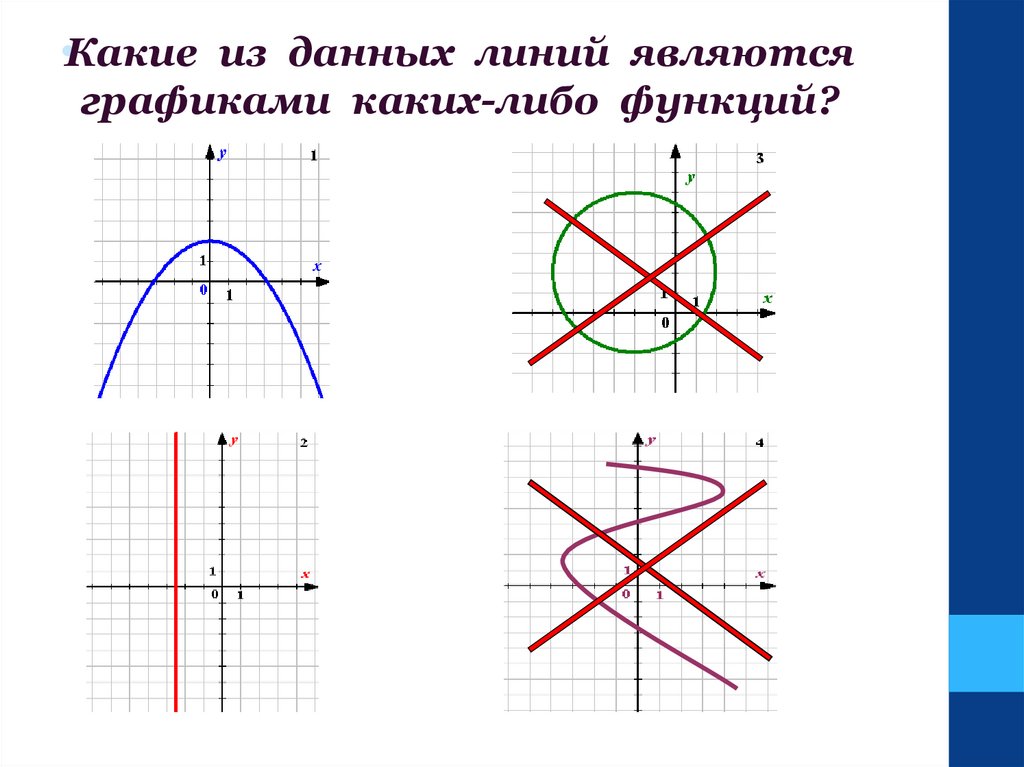
.Какиеиз данных линий являются
графиками каких-либо функций?
12.
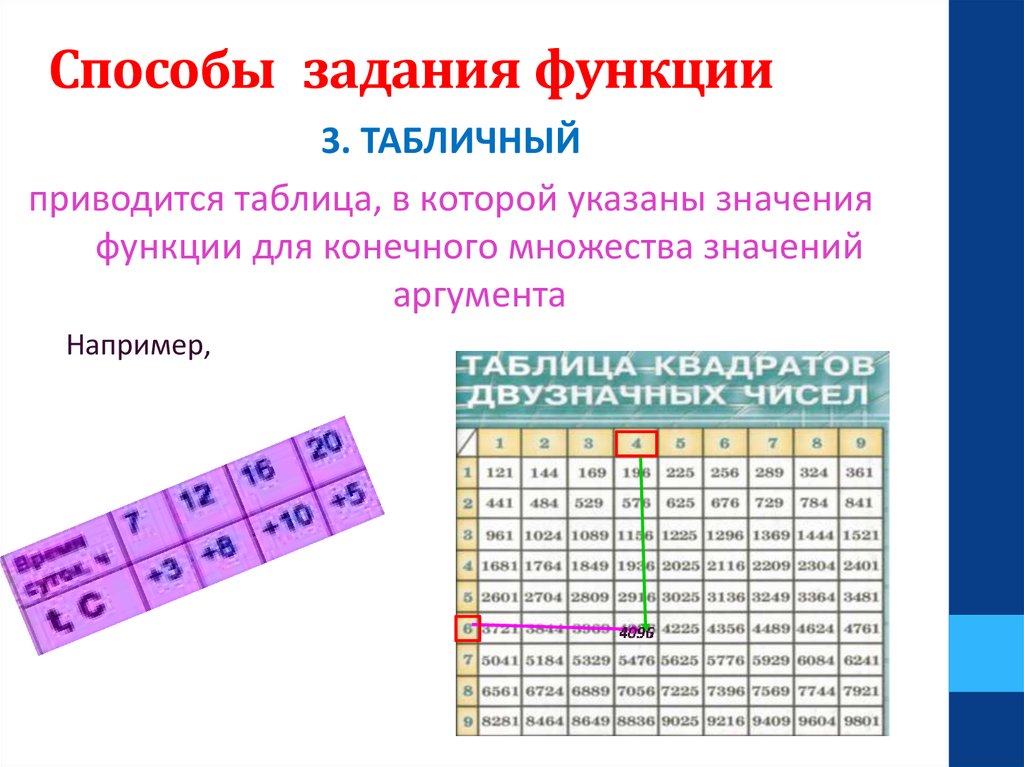
Способы задания функции3. ТАБЛИЧНЫЙ
приводится таблица, в которой указаны значения
функции для конечного множества значений
аргумента
Например,
13.
Способы задания функции4. СЛОВЕСНЫЙ
правило задания функции описывается словами
Например,
Каждому
натуральному
числу ставится в
соответствие куб
этого числа.
14.
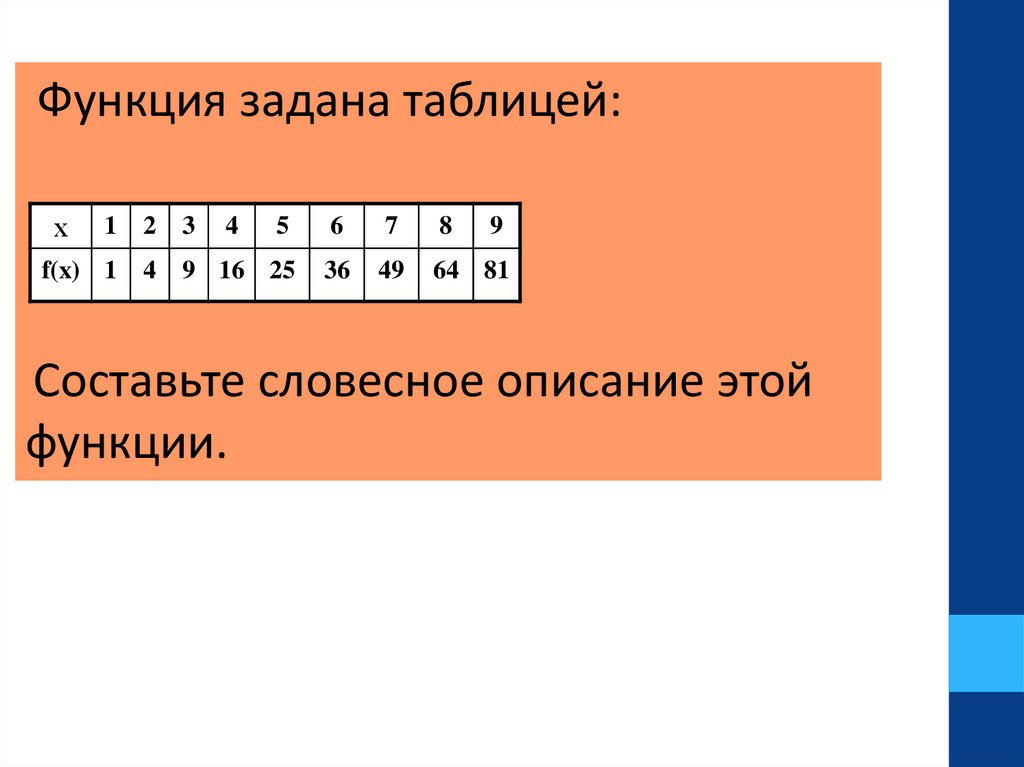
Функция задана таблицей:х
1
2
3
4
5
6
7
8
9
f(x) 1
4
9 16 25
36
49
64 81
Составьте словесное описание этой
функции.
15.
Преобразование графиков функции16.
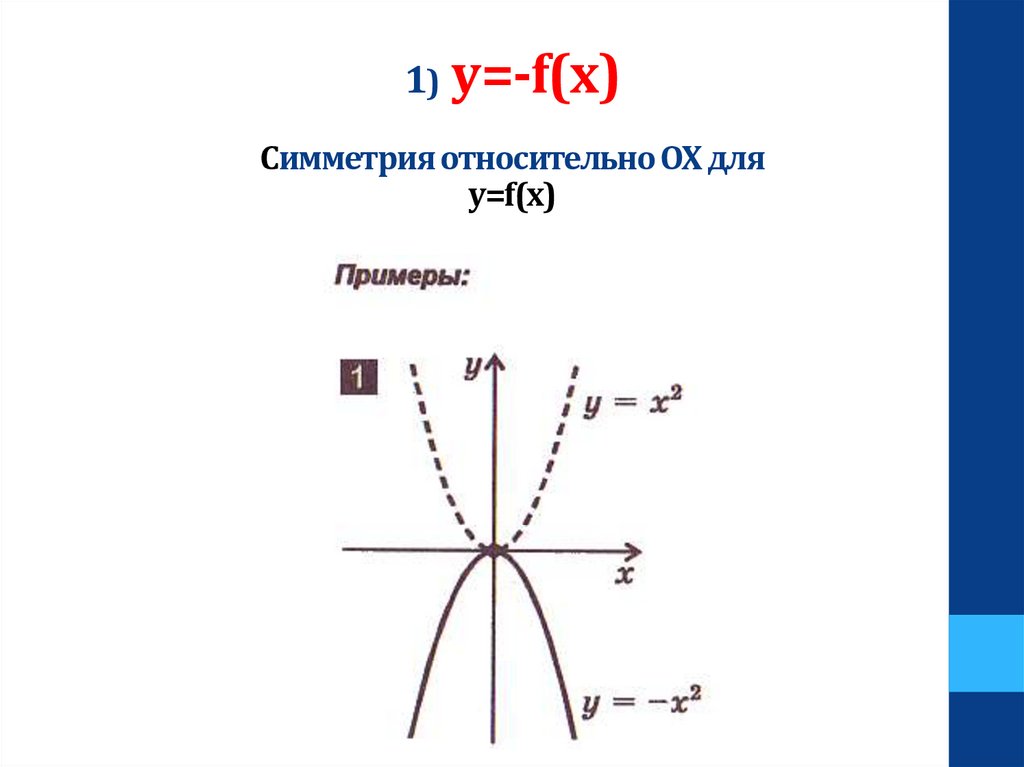
1) y=-f(x)Cимметрия относительно OX для
y=f(x)
17.
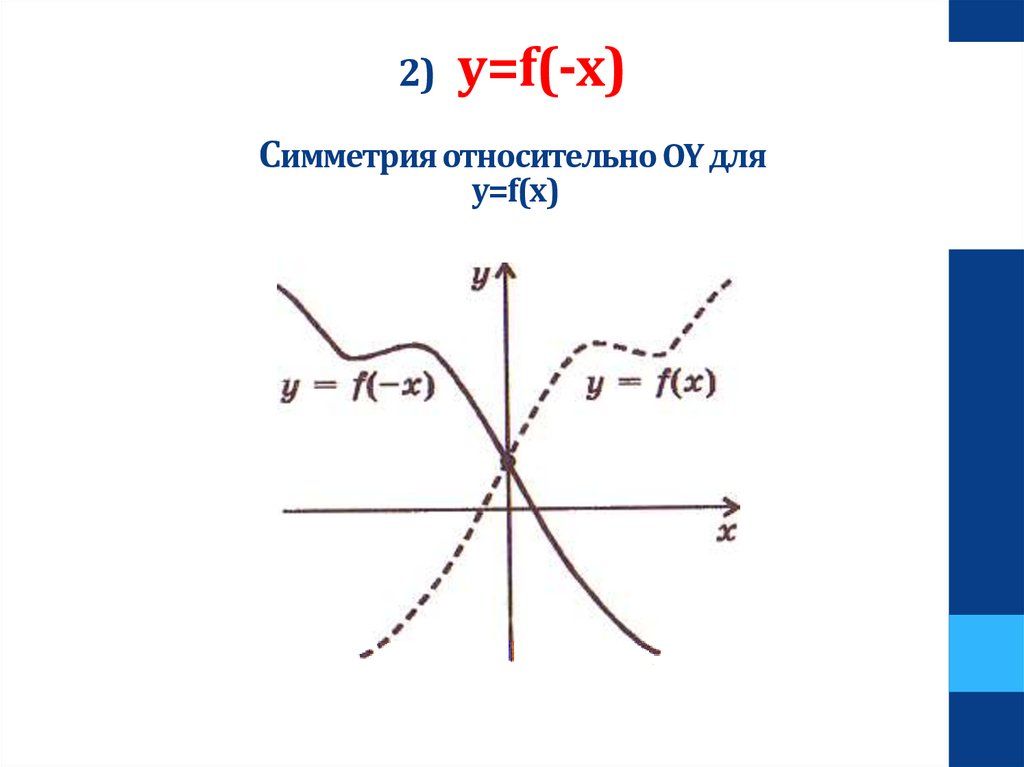
2)y=f(-x)
Симметрия относительно OY для
y=f(x)
18.
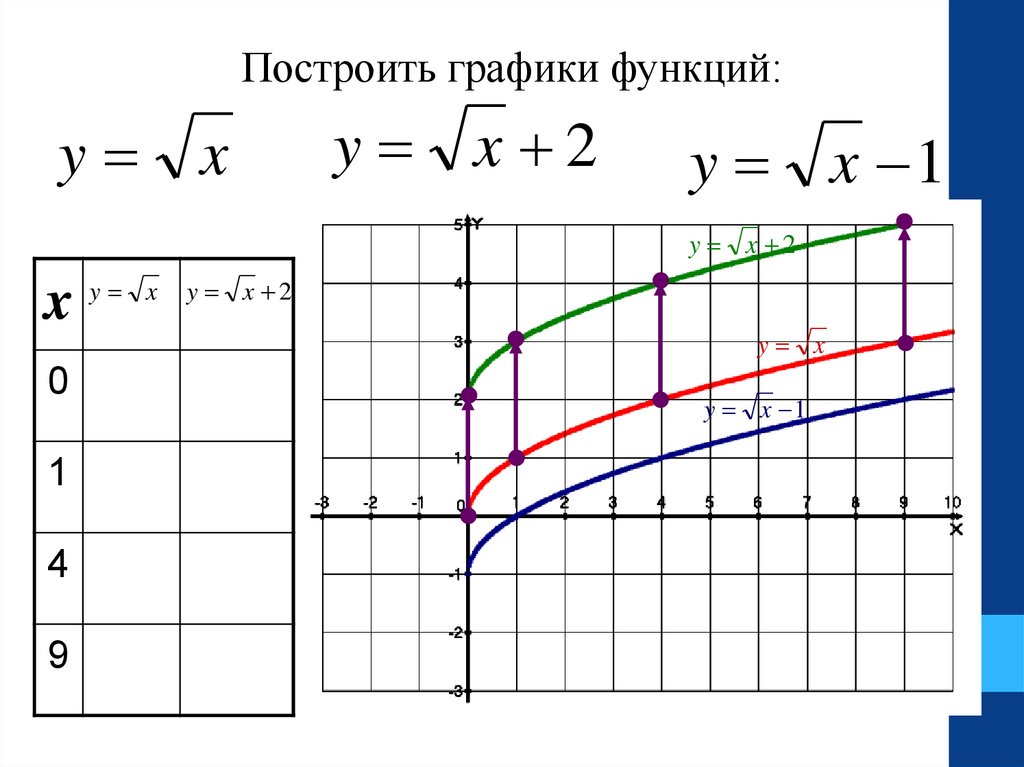
Построить графики функций:y x
y x 2
y x 1
y x 2
x
0
1
4
9
y x
y x 2
y x
y x 1
19.
График функции y x 2 получен врезультате параллельного переноса графика
функции y x на 2 единицы вверх.
График функции y x 1 получен в
результате параллельного переноса графика
функции y x на 1 единицу вниз.
График функции y f x a можно получить в
результате параллельного переноса графика функции
на a единиц вверх, если a 0, и на a единиц
вниз, если a 0 .
20.
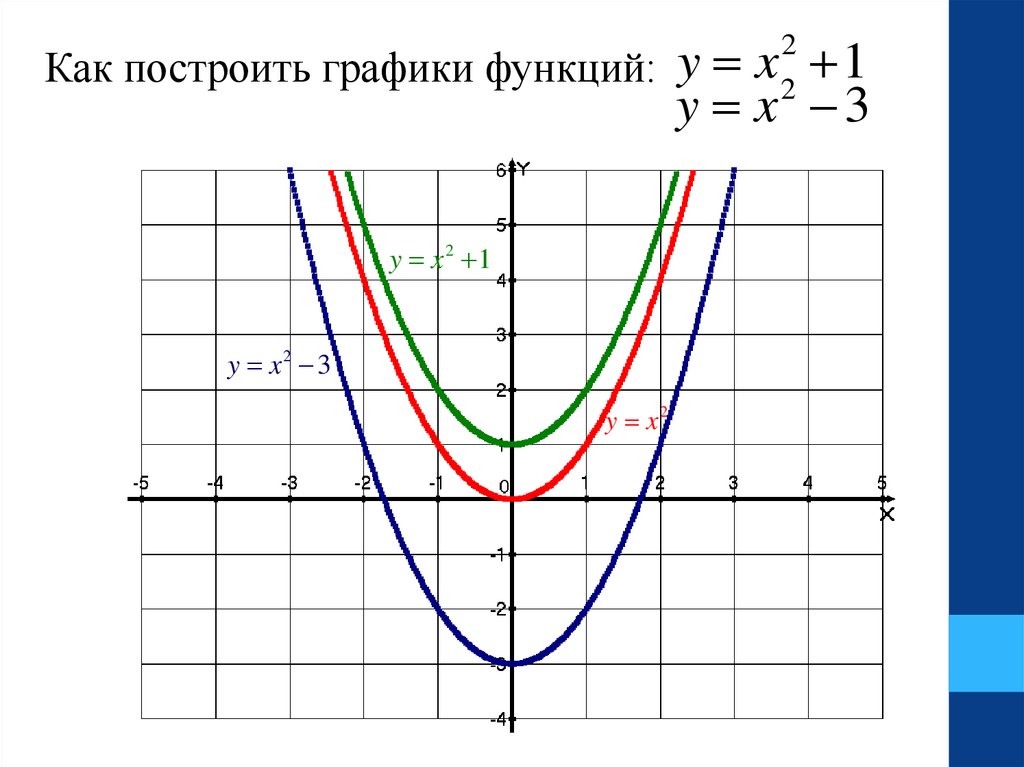
Как построить графики функций: y x 12
2
y x 3
y x2 1
y x2 3
y x2
21.
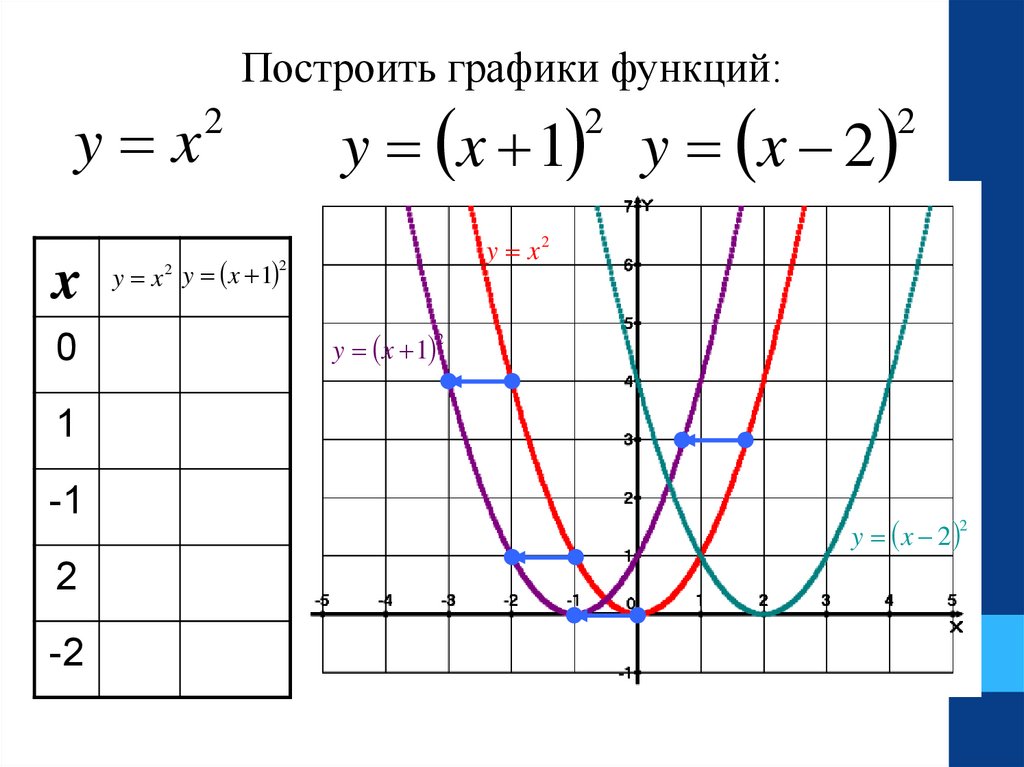
Построить графики функций:y x
x
0
y x 1 y x 2
2
2
2
y x2
y x 2 y x 1
2
y x 1
2
1
-1
2
-2
y x 2
2
22.
График функции y x 1 получен в результате2
параллельного переноса графика функции y x
на 1 единицу влево.
2
График функции y x 2 получен в результате
2
параллельного переноса графика функции y x
на 2 единицы вправо.
2
График функции y f x a можно получить в
результате параллельного переноса графика функции
на a единиц влево, если a 0, и на a единиц
вправо, если a 0 .
23.
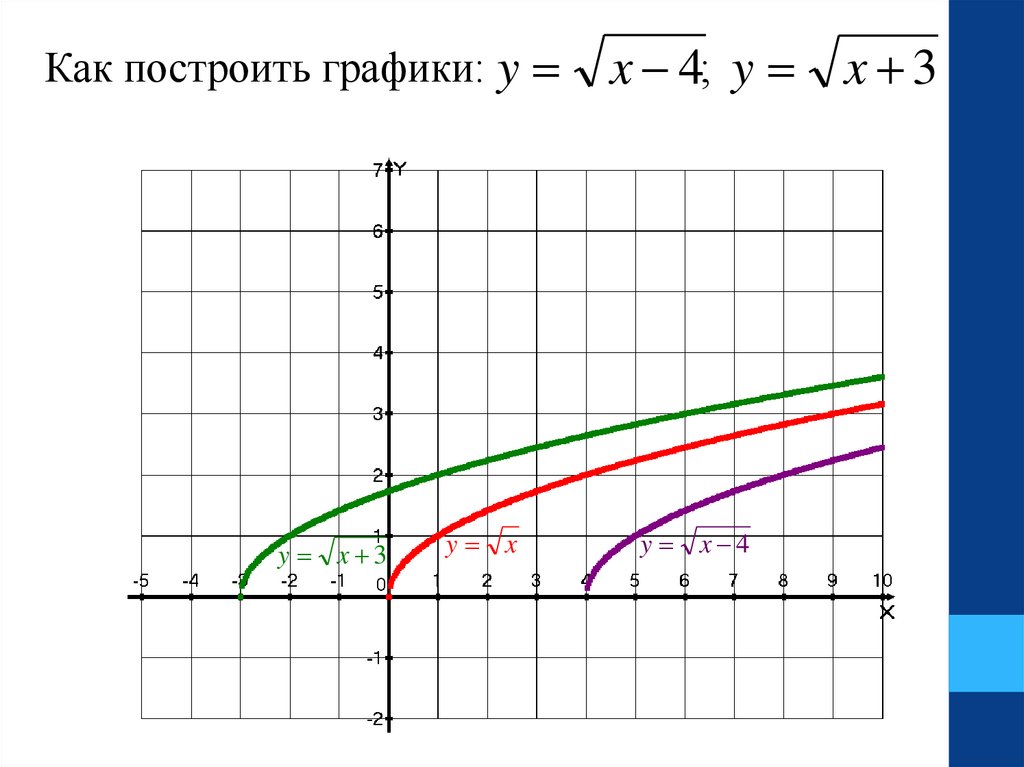
Как построить графики: yy x 3
y x
x 4; y x 3
y x 4
24.
График какой функции изображен на рисунке?а) y x 4
2
б) y x 4
2
в) y x 4
2
г) y x 4
2
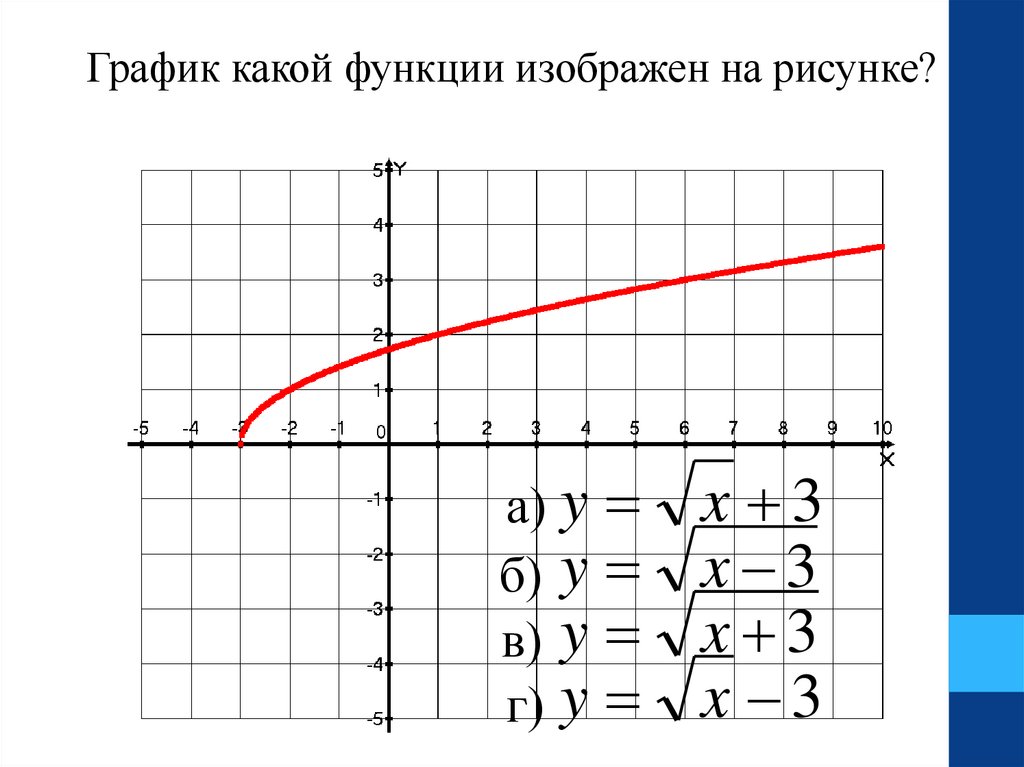
25.
График какой функции изображен на рисунке?а) y
б) y
в) y
г) y
x 3
x 3
x 3
x 3
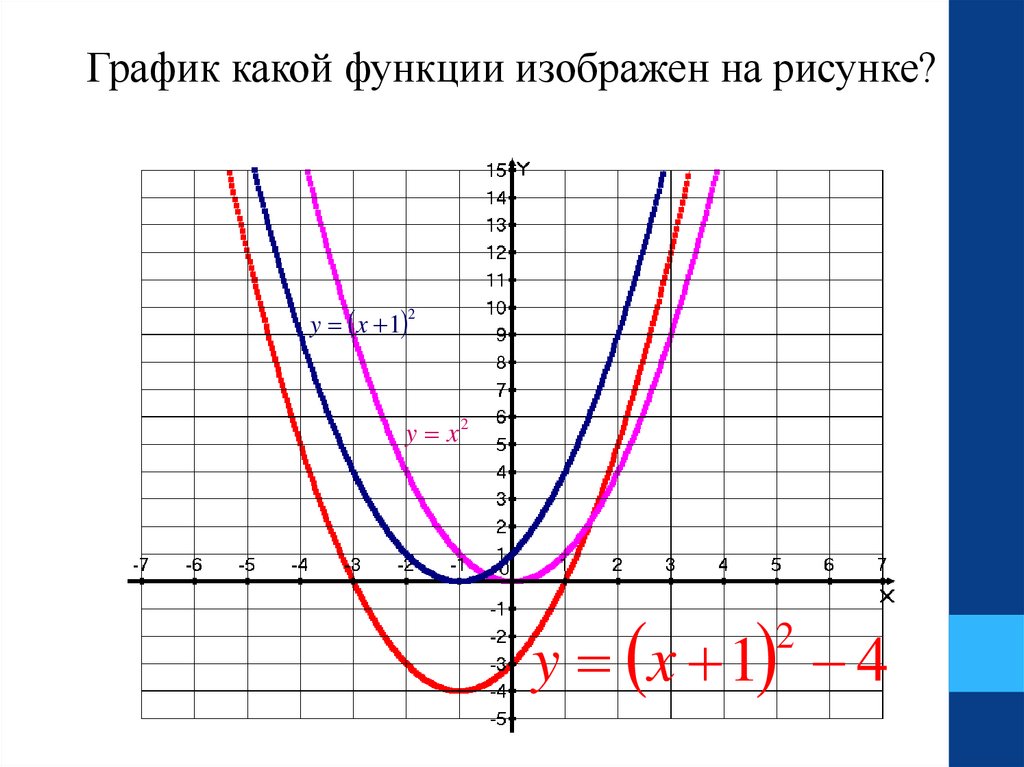
26.
График какой функции изображен на рисунке?y x 1
2
y x2
y x 1 4
2
27.
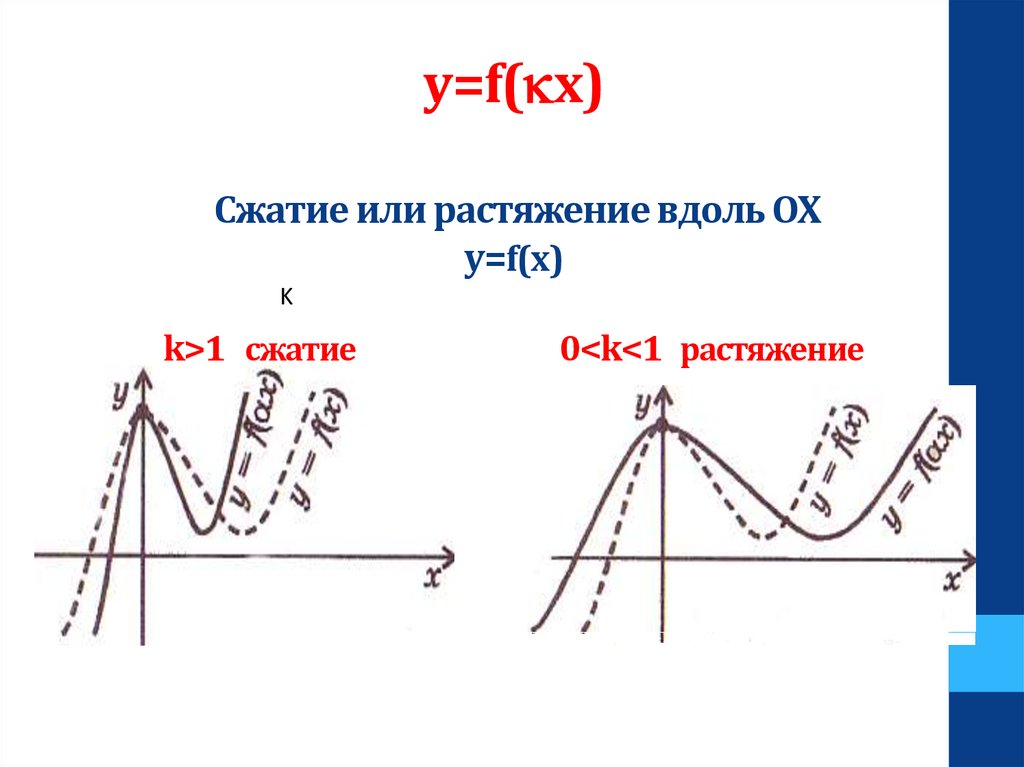
y=f(kx)Сжатие или растяжение вдоль OX
y=f(x)
K
k>1 cжатие
0<k<1 растяжение
28.
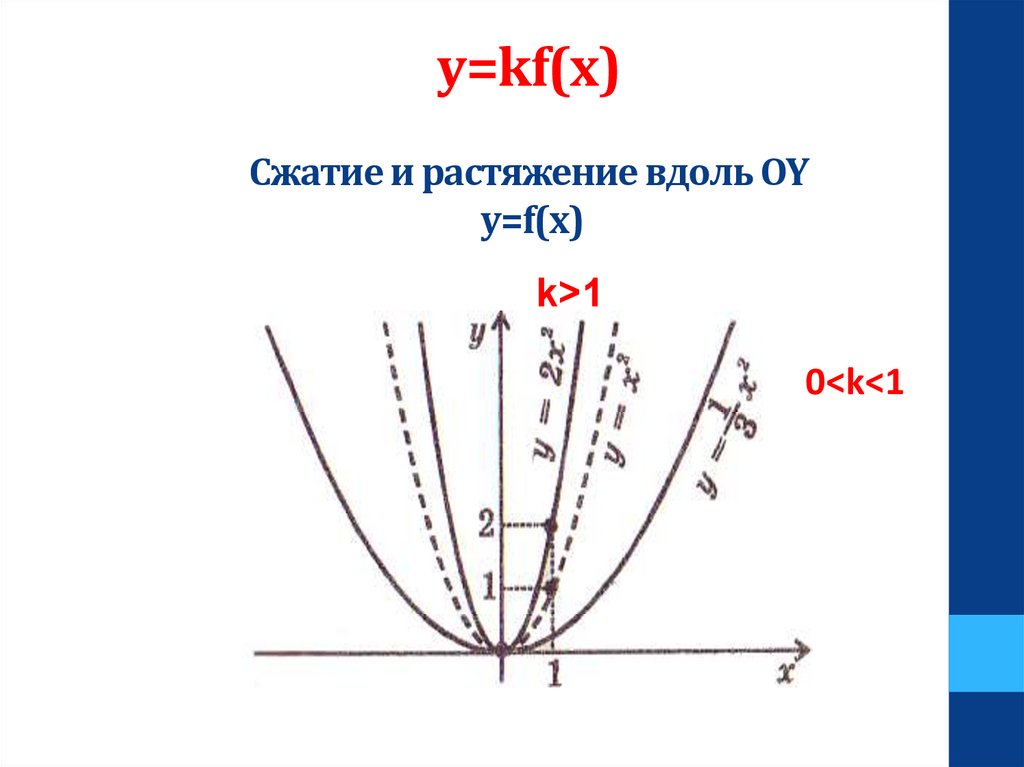
y=kf(x)Сжатие и растяжение вдоль OY
y=f(x)
k>1
0<0<k<1
29.
Домашнее задание:1. Посмотреть видео
https://www.youtube.com/watch?v=yqyzD4bfw7k
1) Ссылка на учебник Алгебра и начала анализа
https://www.okulyk.kz/algebra/515/#6 –
Раздел 1 параграф 1.1 и 1.4. разобрать и ответить
на вопросы после параграфа, с.17 выполнить
задание 1.5
2) Ссылка на приложение Geogebra
https://geogebra.ru.uptodown.com/windows/dow
nload













 mathematics
mathematics








