Similar presentations:
Основные способы преобразования графиков функций
1.
Основные способыпреобразования
графиков функций
2.
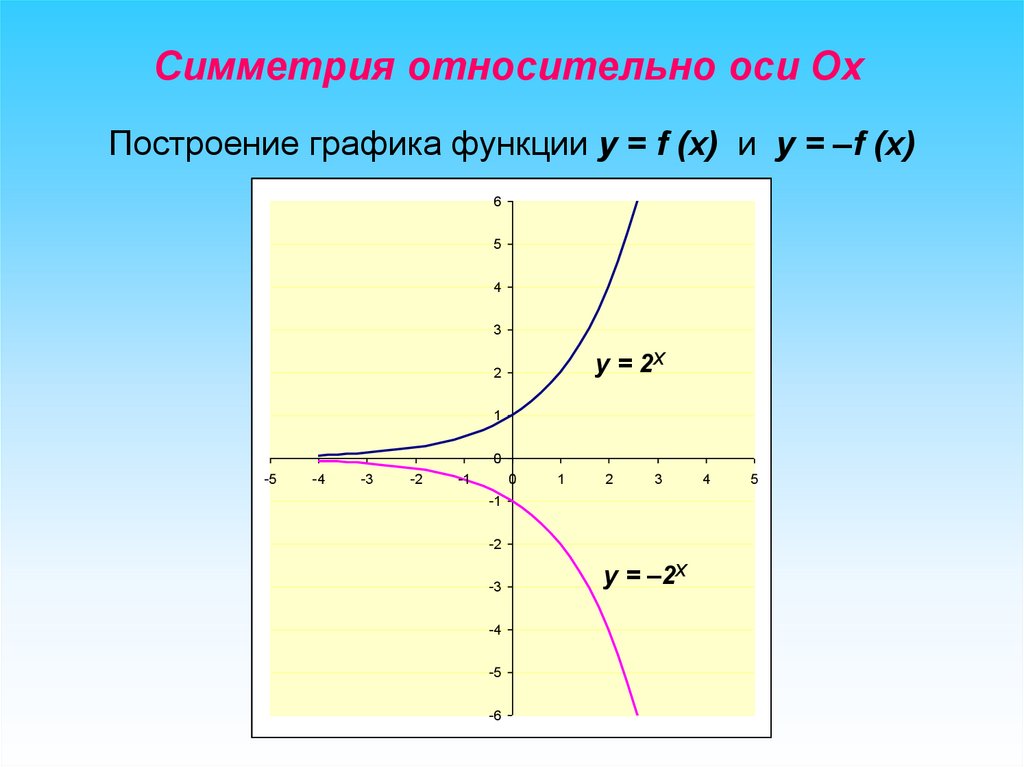
Симметрия относительно оси ОхПостроение графика функции y = f (x) и y = –f (x)
6
5
4
3
у = 2Х
2
1
0
-5
-4
-3
-2
-1
0
1
2
3
-1
-2
-3
-4
-5
-6
у = –2Х
4
5
3.
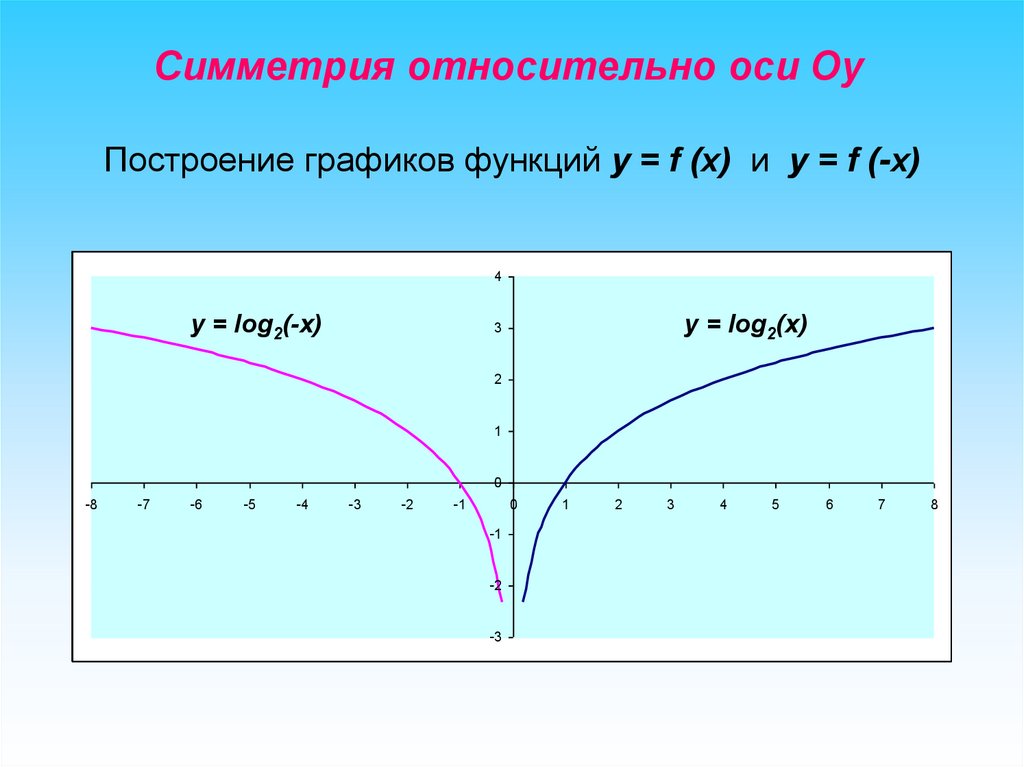
Симметрия относительно оси ОyПостроение графиков функций y = f (x) и y = f (-x)
4
y = log2(-x)
y = log2(x)
3
2
1
0
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
-2
-3
1
2
3
4
5
6
7
8
4.
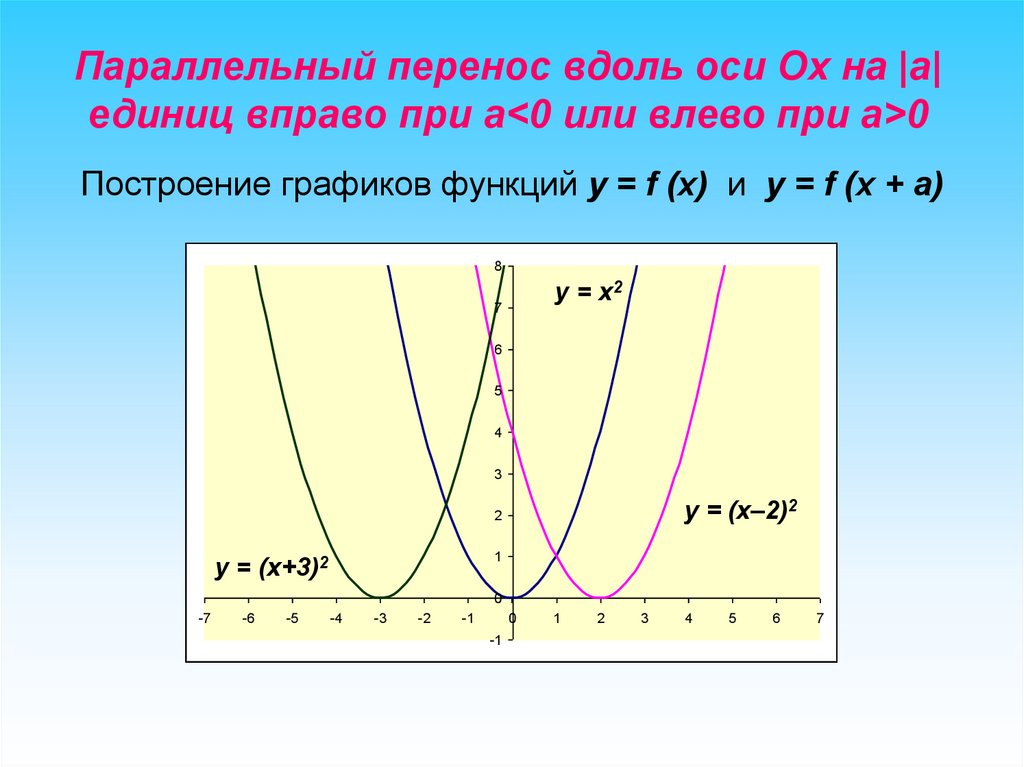
Параллельный перенос вдоль оси Ох на |а|единиц вправо при а<0 или влево при а>0
Построение графиков функций y = f (x) и y = f (x + a)
8
y = x2
7
6
5
4
3
y = (x–2)2
2
1
y = (x+3)2
0
-7
-6
-5
-4
-3
-2
-1
0
-1
1
2
3
4
5
6
7
5.
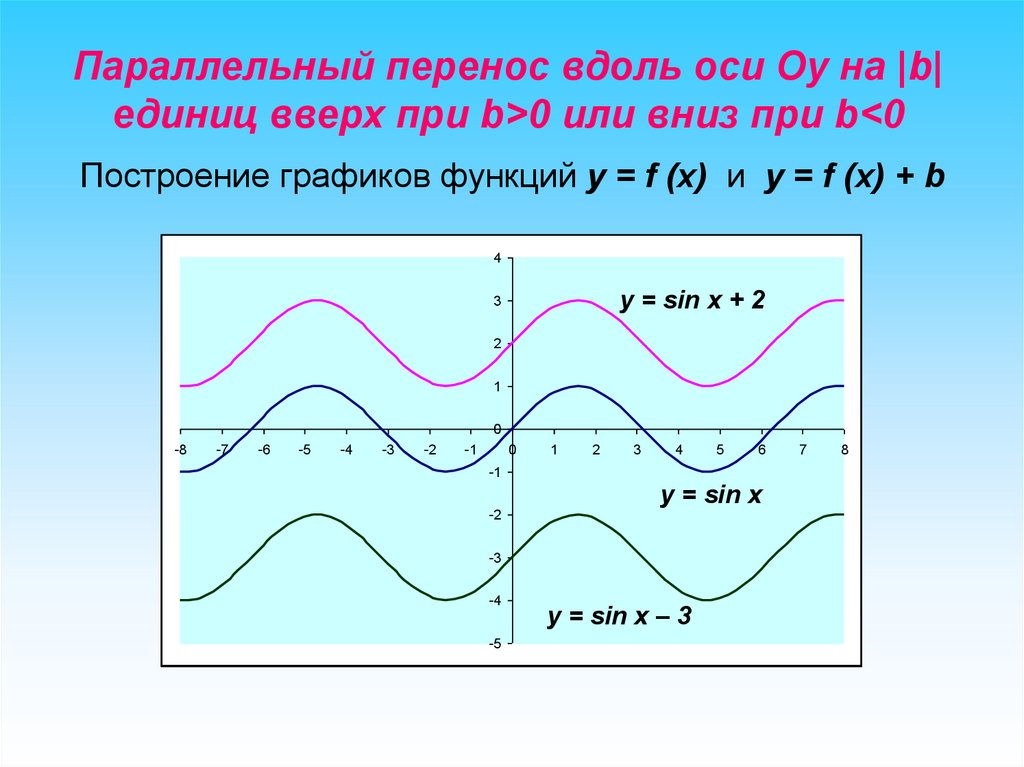
Параллельный перенос вдоль оси Оy на |b|единиц вверх при b>0 или вниз при b<0
Построение графиков функций y = f (x) и y = f (x) + b
4
y = sin x + 2
3
2
1
0
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
-1
-2
y = sin x
-3
-4
-5
y = sin x – 3
7
8
6.
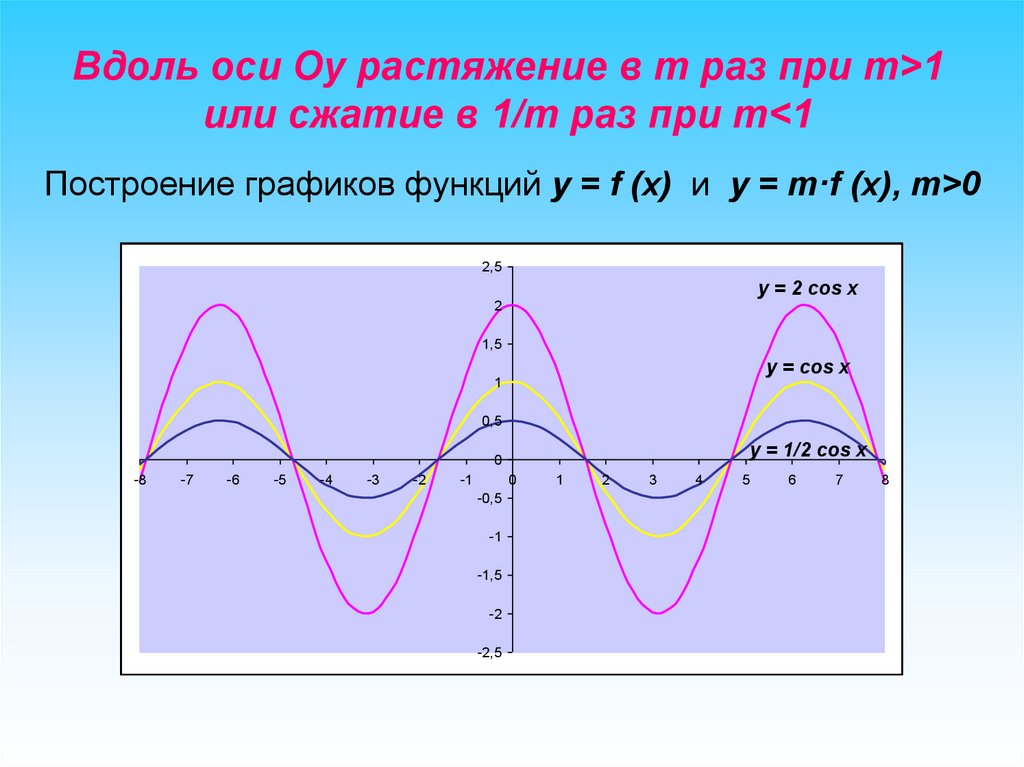
Вдоль оси Oy растяжение в m раз при m>1или сжатие в 1/m раз при m<1
Построение графиков функций y = f (x) и y = m·f (x), m>0
2,5
y = 2 cos x
2
1,5
y = cos x
1
0,5
y = 1/2 cos x
0
-8
-7
-6
-5
-4
-3
-2
-1
0
-0,5
-1
-1,5
-2
-2,5
1
2
3
4
5
6
7
8
7.
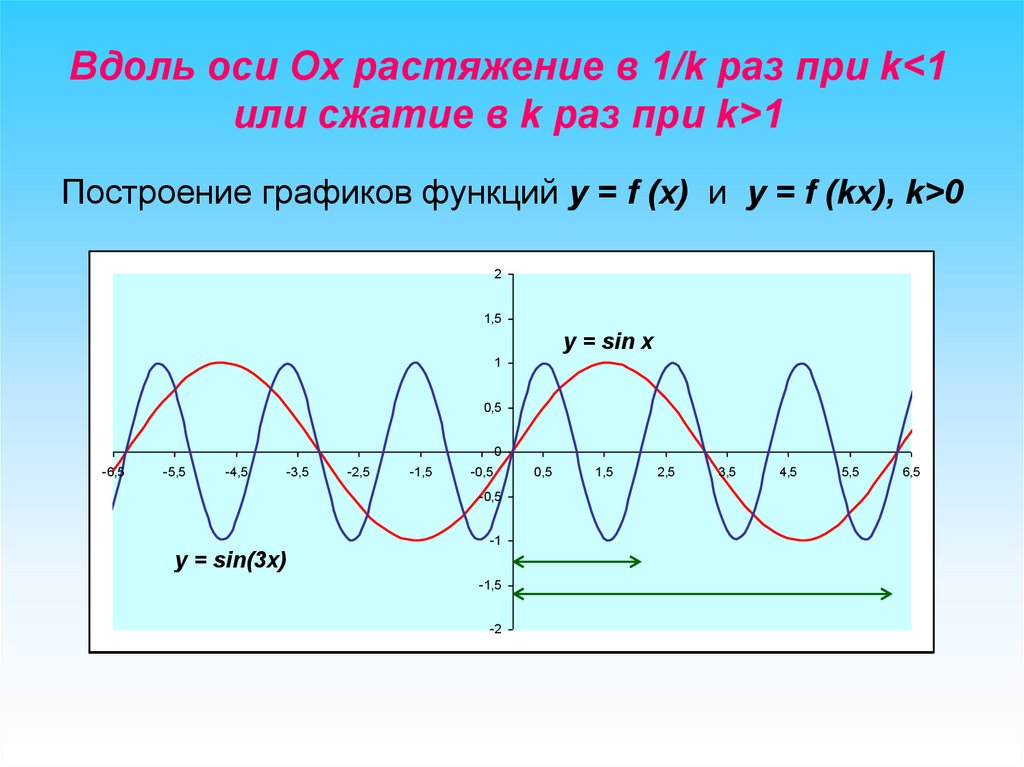
Вдоль оси Ox растяжение в 1/k раз при k<1или сжатие в k раз при k>1
Построение графиков функций y = f (x) и y = f (kx), k>0
2
1,5
y = sin x
1
0,5
0
-6,5
-5,5
-4,5
-3,5
-2,5
-1,5
-0,5
-0,5
-1
y = sin(3x)
-1,5
-2
0,5
1,5
2,5
3,5
4,5
5,5
6,5
8.
Построение графика функции y = m·f(kx+a)+b, m>0, k>0a
1) Переписать функцию в виде y = m·f(k(x+ k ))+b;
2) Построить последовательно графики функций:
y = f(x)
y = f(kx)
a
y = f(k(x+ k ))
y = m·f(k(x+ a ))
k
a
y = m·f(k(x+ k ))+b
9.
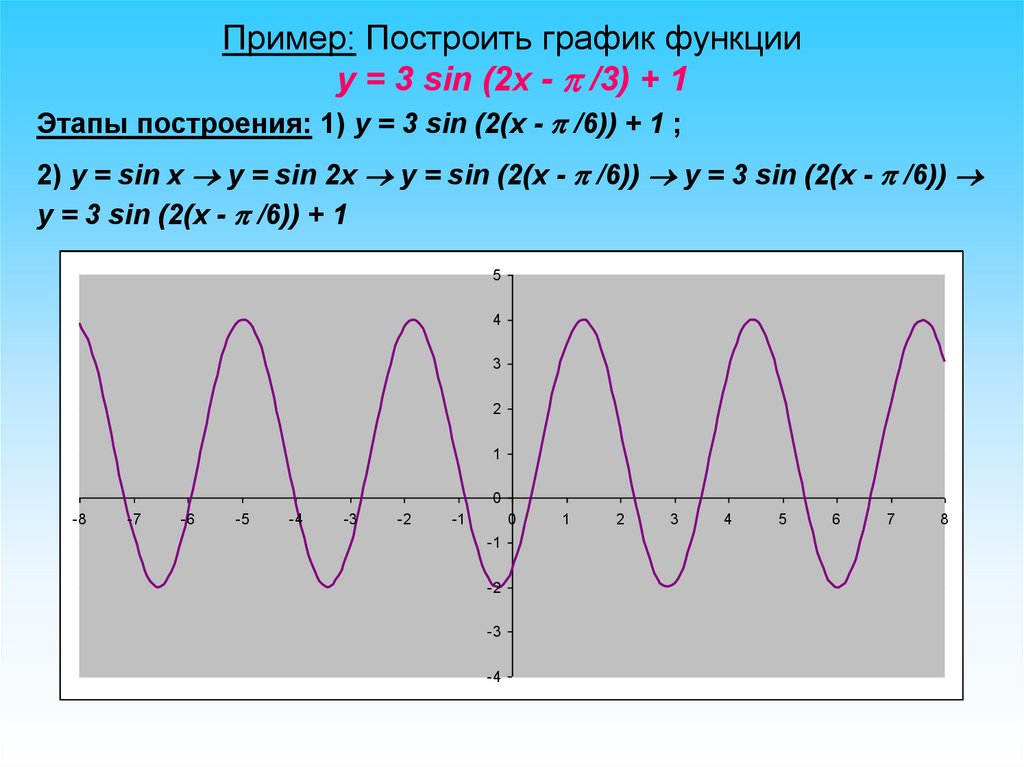
Пример: Построить график функцииy = 3 sin (2x - /3) + 1
Этапы построения: 1) y = 3 sin (2(x - /6)) + 1 ;
2) y = sin x y = sin 2x y = sin (2(x - /6)) y = 3 sin (2(x - /6))
y = 3 sin (2(x - /6)) + 1
5
4
3
2
1
0
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
10.
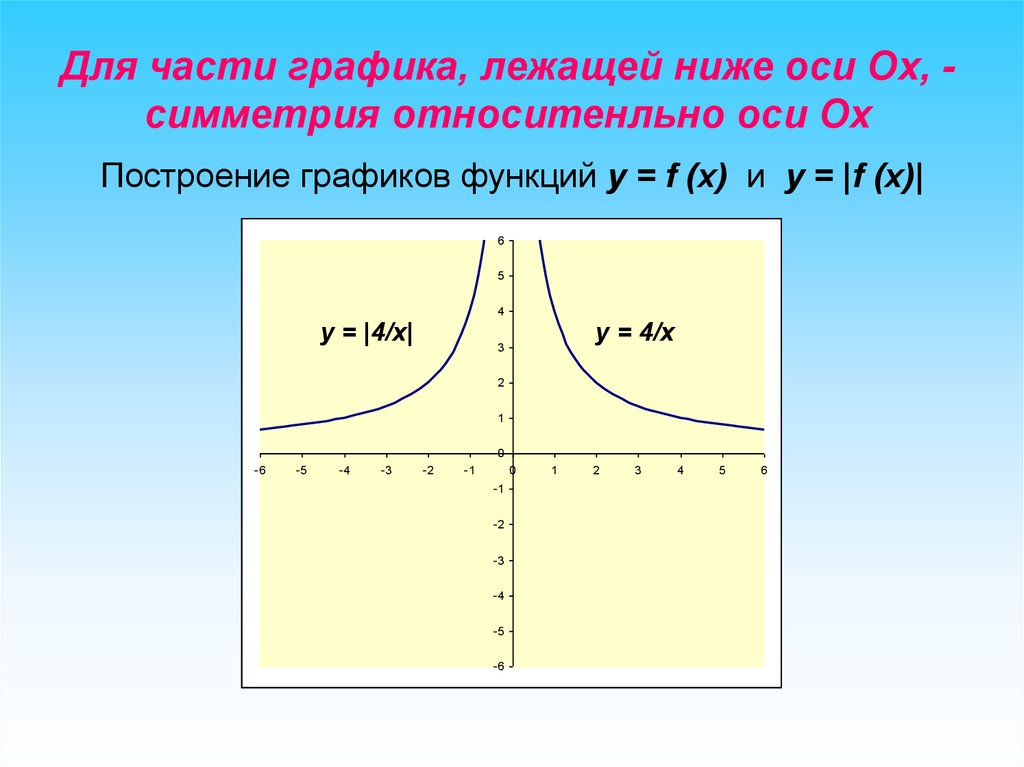
Для части графика, лежащей ниже оси Ох, симметрия относитенльно оси ОхПостроение графиков функций y = f (x) и y = |f (x)|
6
5
4
y = |4/х|
y = 4/х
3
2
1
0
-6
-5
-4
-3
-2
-1
0
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
11.
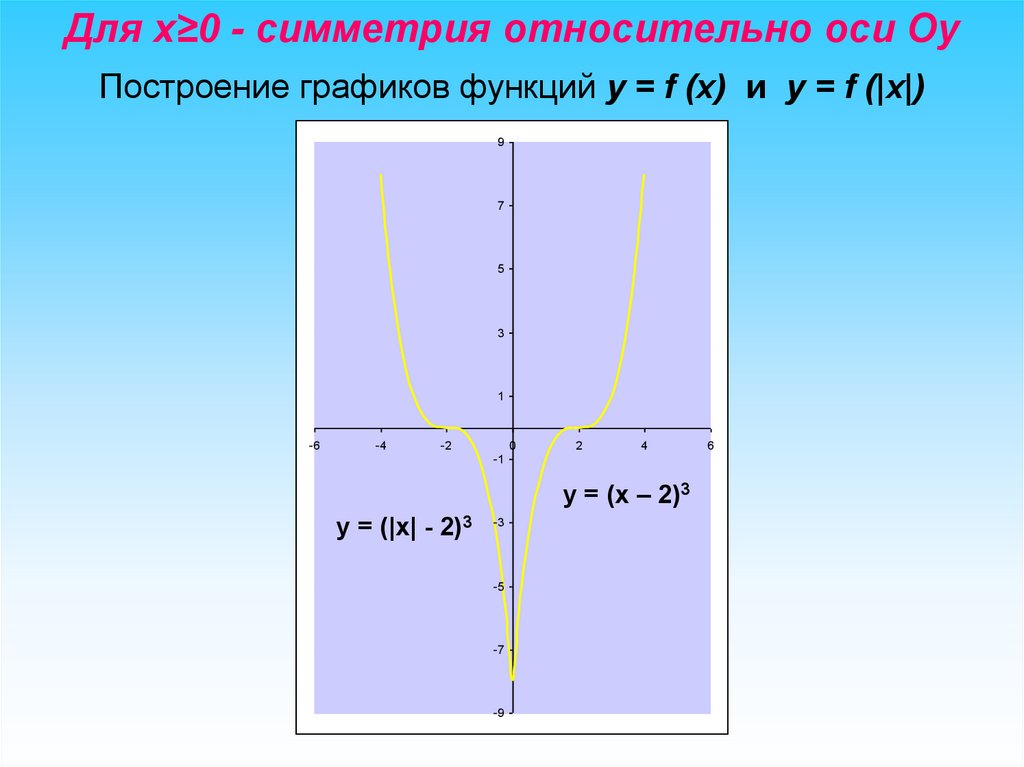
Для х≥0 - симметрия относительно оси ОyПостроение графиков функций y = f (x) и y = f (|x|)
9
7
5
3
1
-6
-4
-2
0
2
4
-1
y = (х – 2)3
y = (|x| - 2)3
-3
-5
-7
-9
6
12.
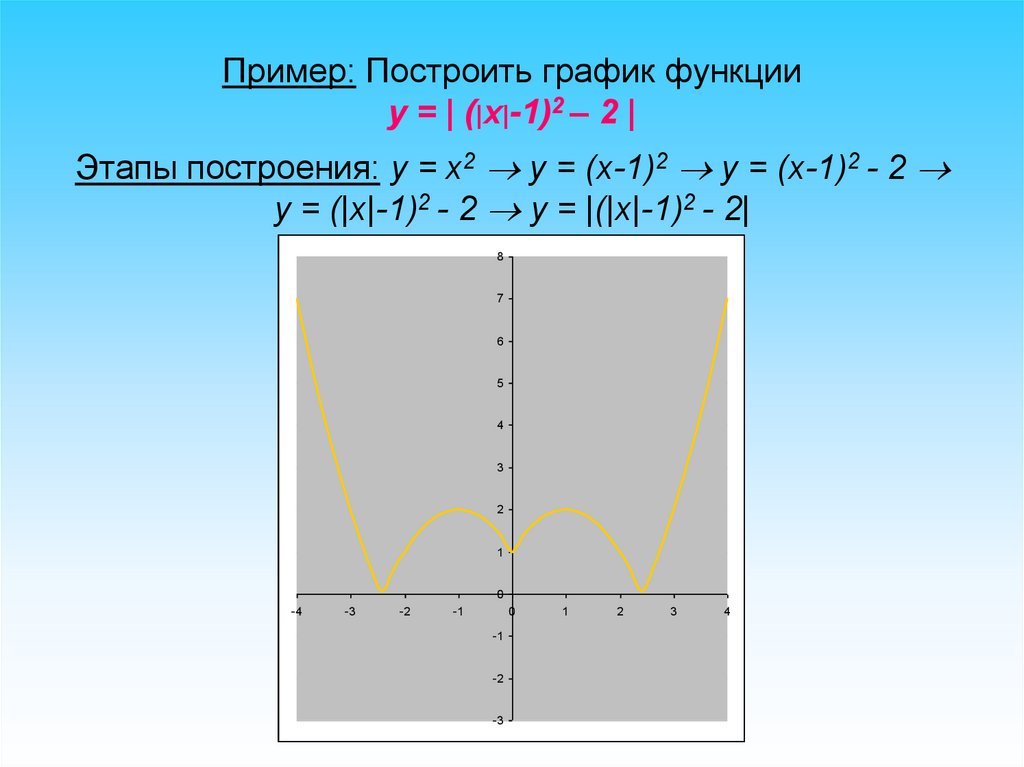
Пример: Построить график функцииy = | (|х|-1)2 – 2 |
Этапы построения: y = x2 y = (x-1)2 y = (x-1)2 - 2
y = (|x|-1)2 - 2 y = |(|x|-1)2 - 2|
8
7
6
5
4
3
2
1
0
-4
-3
-2
-1
0
-1
-2
-3
1
2
3
4
13.
Задание. С помощью элементарных преобразованийпостройте графики функций, предварительно расписав
последовательность построений:
1) у = 1/2 sin (3x) – 2
2) y = 2 3x+1 – 4
3) y = 2 (x – 1)2 – 3
4) y = –3 log2(x + 1)
5) у 2 х 1
3
6) у
1
х 2
4
7) у
2
х 4


 mathematics
mathematics








