Логарифмические уравнения

1.

Решение
логарифмических
уравнений
Урок изучения новой темы

2.

Цель урока:
обобщить материал по свойствам
логарифмов, логарифмической функции;
рассмотреть основные методы решения
логарифмических уравнений;
развивать навыки устной работы.

3.

Вспомни и продолжи свойство!
log a (bc) log a b log a c
b
log a
c
log a b log a c
log a b r log a b
r
log a r b
1
log a b
r
log c b
log a b
log c a

4.

Вычислите значения выражения
log 2 8
log 5 5
lg 100
log 7 1
log 5 125
lg 0,01
log 4 64
1
log 3
27
log 0,5 32
log 1 9
3
log 2
2
log 3 81
2 log2 5
10 lg15

5.

Вычислить значение выражения
log 8 16 log 8 4
log 3 33 log 3 11
lg 34 lg 3,4 lg 25 lg 4
log 3 log 3 27 log 2 log 2 16
3
2 log3 18
log 5 49
log 5 7
5
log5 2 1
log 3 64
log 3 4

6.

Определение:
Уравнения, содержащие неизвестное под знаком
логарифма или в основании логарифма
называются логарифмическими.
log a f ( x) b
log f ( x ) b a

7.

Методы решения ЛУ:
1.Применение определения
логарифма
2.Введение
новой переменной
Вид уравнения
log a f ( x) b
log 2a f ( x) b log a f ( x) c 0
3. Приведение к одному и
тому же основанию
4. Метод потенцирования
log a f ( x) log a g ( x)
5 Метод логарифмирования
обеих частей уравнения
6. Функциональнографический метод
log a f ( x) g ( x)

8.

log x 5 log 3 x 6 0
2
3
ОДЗ : x 0
Обозначим log 3 x t
t 2 5t 6 0
t1 3, t 2 2
1) log 3 x 3
x 33 27
2) log 3 x 2
x 3 9
2
Ответ : 9;27.

9.

Решение простейшего логарифмического уравнения
log a f ( x) b, где a 0, a 1
основано на применении определения логарифма и
решении равносильного уравнения
Пример
f ( x) a
log 2 3 x 5 4
3x 5 24
3 x 16 5
3 x 21
x 7
b

10.

Метод потенцирования
• Под потенцированием понимается переход от
равенства, содержащего логарифмы, к равенству, не
содержащему их:
если loga f(х) = loga g(х),
то f(х) = g(х),
решив полученное равенство, следует сделать
проверку корней.

11.

Пример :
log 7 (3x 4) log 7 (5 x 8)
3x 4 5 x 8
3x 5 x 8 4
2x 4
x 2
Проверка : при x 2
левая и правая части уравнения не имеют смысла
Ответ : нет решений

12.

Если в уравнении содержатся логарифмы с разными
основаниями, то прежде всего следует свести все логарифмы к
одному основанию, используя формулы перехода
log c b
1
1
log a b
; log a b
; log a r b log a b
log c a
log b a
r
Пример :
log 2 x 2 log 1 x 9;
2
ОДЗ : x 0
log 2 x 2 log 2 1 x 9;
log 2 x 2 log 2 x 9;
3 log 2 x 9;
log 2 x 3;
x 8 ОДЗ
Ответ : x 8

13.

Если в показатели степени содержится логарифм, то обе части уравнения
логарифмируют по тому основанию, которое содержится в основании
логарифма, находящегося в показателе степени.
x log3 x 1 9;
ОДЗ : x 0, x 1
Логарифмир уем обе части уравнения по основанию 3
log 3 x log3 x 1 log 3 9;
(log 3 x 1) log 3 x 2;
log 32 x log 3 x 2 0;
пусть log 3 x t , тогда
t 2 t 2 0;
t 1 2, t 2 1;
1) log 3 x 2;
1
9;
2) log 3 x 1;
x
1
x 3; Ответ : ;3.
9

14.

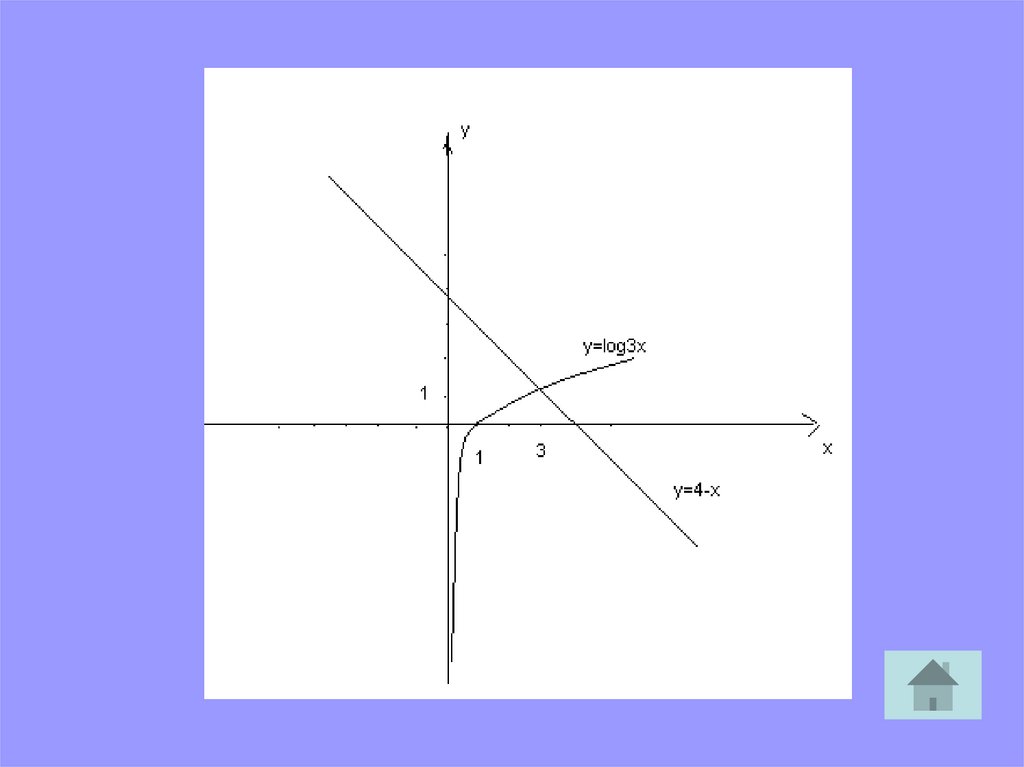
Для решения ЛУ графическим методом надо построить
в одной и той же системе координат графики функций,
стоящих в левой и правой частях уравнения и найти
абсциссу их точки пересечения
Пример
log3 х = 4-х.
• Так как функция у= log3 х возрастающая, а функция у
=4-х убывающая на (0; + ∞ ),то заданное уравнение
на этом интервале имеет один корень.