Similar presentations:
Логарифмические уравнения
1. «Логарифмические уравнения»
«ЛОГАРИФМИЧЕСКИЕУРАВНЕНИЯ»
2.
ОпределениеУравнение, содержащее
переменную под знаком
логарифма, называется
логарифмическим log x b
a
Где a 0 , a
x a
b
1
Оно имеет единственное решение
при любом b.
3.
Основные методы решениялогарифмических уравнений
1) по определению логарифма;
например, уравнение loga х = b (а > 0,
а≠ 1, b>0 ) имеет решение х = аb.
2) функционально-графический метод;
4.
3) метод потенцирования;Под потенцированием понимается
переход от равенства,
содержащего логарифмы, к
равенству, не содержащему их:
если , loga f(х) = loga g(х), то f(х) =
g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1.
5.
4. Метод введение новой переменной.5. Метод логарифмирования обеих
частей уравнения.
6. Метод приведения логарифмов к
одному и тому же основанию.
6.
Этапы решения уравнения•Найти область допустимых
значений (ОДЗ) переменной
•Решить уравнение, выбрав метод
решения
•Проверить найденные корни
непосредственной
подстановкой в исходное уравнение
или выяснить, удовлетворяют ли
они условиям ОДЗ
7.
Виды простейших логарифмическихуравнений и методы их решения
Уравнение
Решение
а) log a x b, a 0 и a 1
б) log a f ( x ) b, a 0 и a 1.
в) log a f ( x ) log a g( x ) ,
a 0 и a 1.
г) log g ( x ) f ( x ) b
x ab
f ( x) ab
f ( x ) 0,
g ( x ) 0,
f ( x ) g ( x ).
g( x ) 0,
g( x ) 1,
f ( x ) g ( x )b
8.
ПРИ КАКИХ ЗНАЧЕНИЯХ Х СУЩЕСТВУЕТЛОГАРИФМ
log x 3
1
4
log 10 x
5
Решить простейшее логарифмическое уравнение
9. Найдите число x
log 5 x 22
25
x 5
log 3 x 1
1
xx 31
3
log 1 x 2
6
2
1 2
x
6
xx 36
6
log
5
x 0
51
x
x
0
10.
Решить уравнения:1. log3(5х – 1) = 2.
11.
Решить уравнения:2. log2(х – 5) + log2(х + 2) = 3.
12.
Решить уравнения:3. log3 (x2 – 3x – 5) = log3 (7 – 2x).
13.
Введение новой переменной2
A loga
f ( x) B loga f ( x) C 0,
где a > 0, a 1, A, В, С – действительные
числа.
Пусть t = loga f(x), t R. Уравнение
примет вид t2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga
f(x). Учитывая область определения, выберем
только те значения x, которые удовлетворяют
неравенству f(x) > 0.
14.
Пример 1.Решить уравнение lg 2 x – lg x – 6 = 0.
Решение. Область определения
уравнения – интервал (0; ).
Введём новую переменную t = lg x, t R.
Уравнение примет вид t 2 – t – 6 = 0.
Его корни t1 = –2, t2 = 3.
15.
Вернёмся к первоначальнойпеременной lg x = –2 или lg x = 3,
х = 10 –2 или х = 10 3.
Оба значения x удовлетворяют
области определения данного
уравнения (х > 0).
Ответ. х = 0,01; х = 1000.








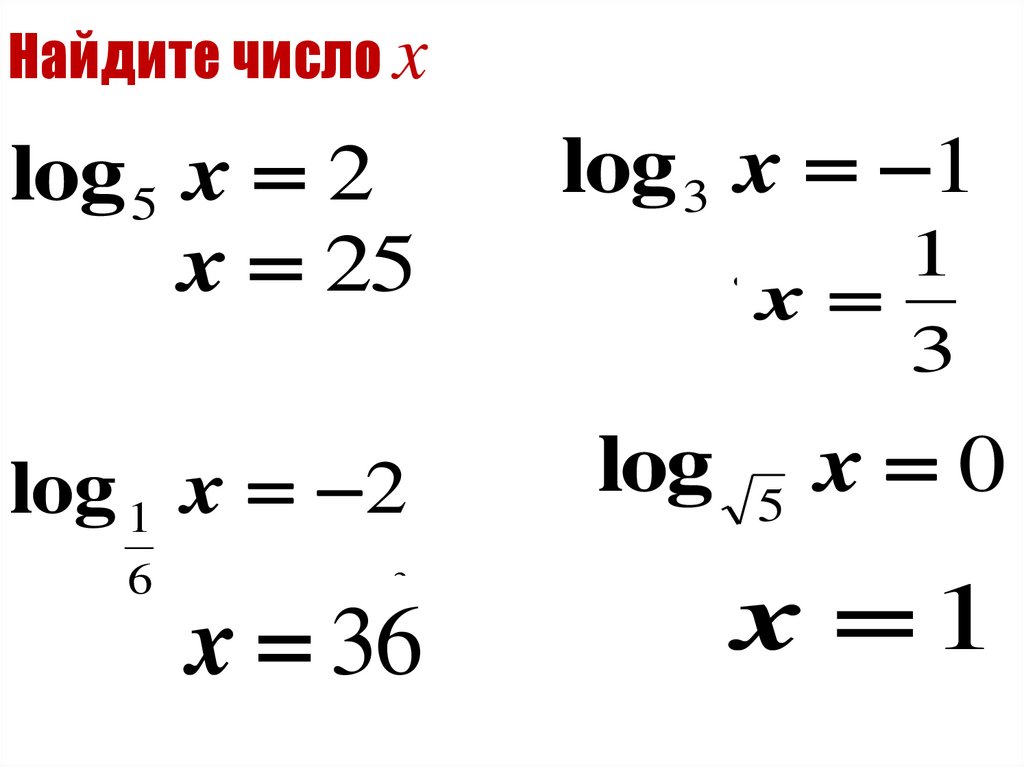







 mathematics
mathematics








