Тригонометрические функции y = sin x и y = cos x их свойства и графики

1.

2.

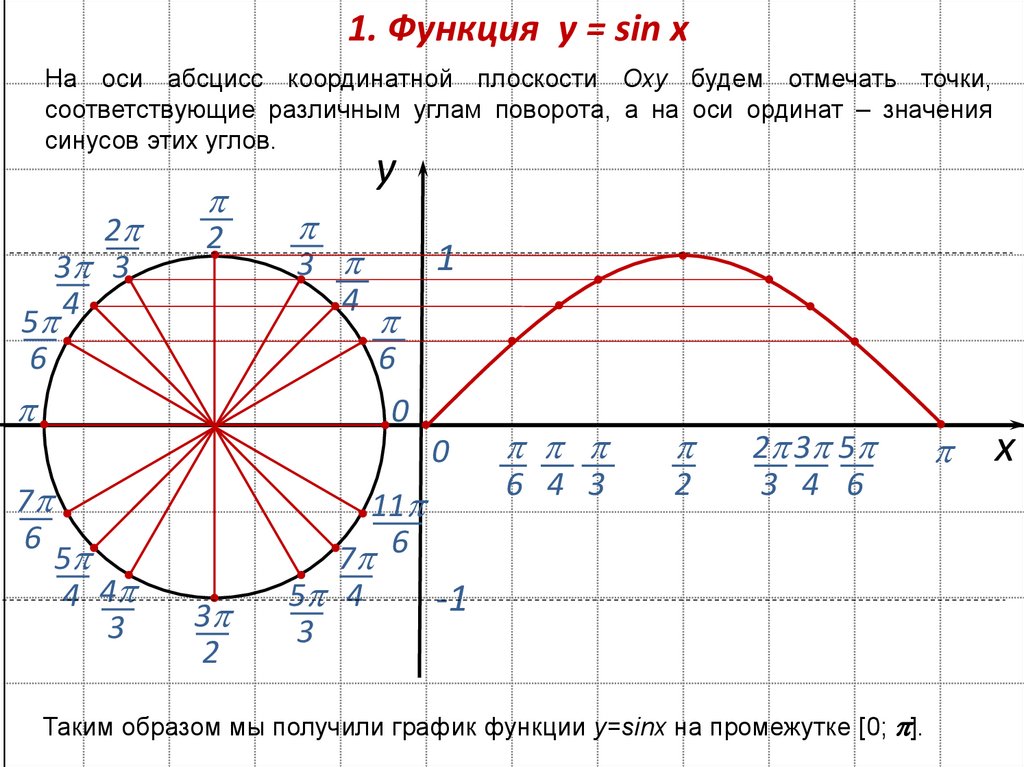
1. Функция y = sin x
На оси абсцисс координатной плоскости Оху будем отмечать точки,
соответствующие различным углам поворота, а на оси ординат – значения
синусов этих углов.
2
3 3
4
2
5
6
y
3
4
1
6
0
0
7
6
5
4 4
3
3
2
11
7 6
5 4
-1
3
6 4 3
2
2 3 5
3 4 6
Таким образом мы получили график функции y=sinx на промежутке [0; ].
х

3.

y = sin x
2
3 3
4
2
5
6
3
4
6
7
6
0
5
4 4
3
11
6
7
3
2
7 5 4
6 4 3
3
2
5 7 11 2
3 4 6
5 4
3
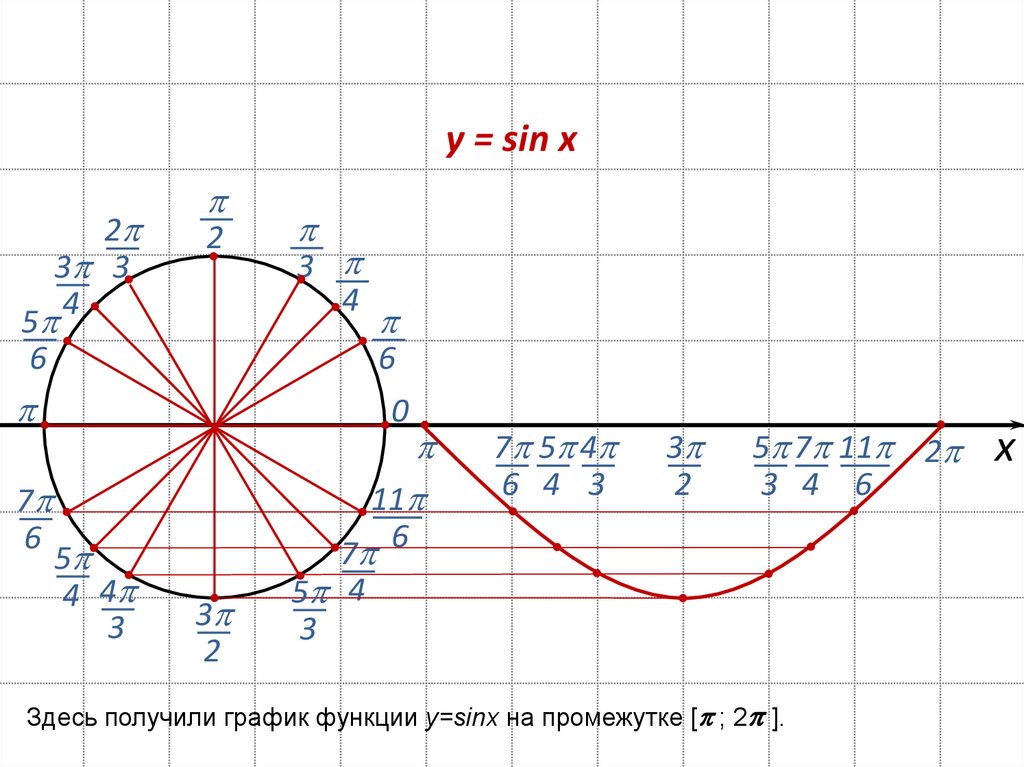
Здесь получили график функции y=sinx на промежутке [ ; 2 ].
х

4.

y
3
2
y = sin x
1
-3
2
5 -2 - - -
7
6 3 2 3 6
6
0
6 3
-1
-2
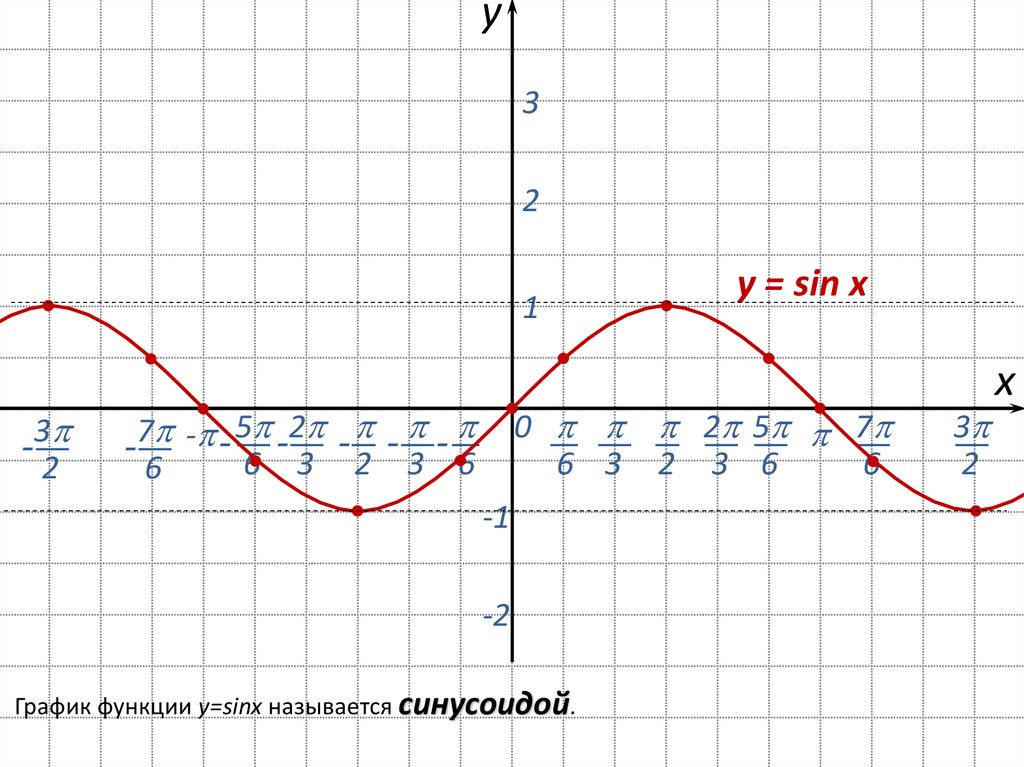
График функции y=sinx называется синусоидой.
2 5 7
2
3 6
6
3
2
х

5.

На практике, для построения графика функции у=sinx на промежутке [0; ],
сначала отмечают точки с координатами (0; 0), ( /6; 0,5), ( /2; 1), ( 5 /6; 0,5)
и ( ; 0). Они образуют своеобразную «арку», которая периодически (с
периодом ) отображается симметрично оси Ох.
y
1
5
6
2
3
2
2
3
2
1
2
6
0
1
6
2
2
5
6
2
−1
После этого используют свойство периодичности функции у=sinx. Так как
наименьший положительный период функции y=sinx равен 2 , то
изображенный участок графика можно параллельно переносить влево и
вправо вдоль оси Ох на 2 n (n ) единичных отрезков.
График функции y=sinx называется синусоидой.
x

6.

Свойства функции у = sin x
1.
2.
3.
4.
5.
6.
7.
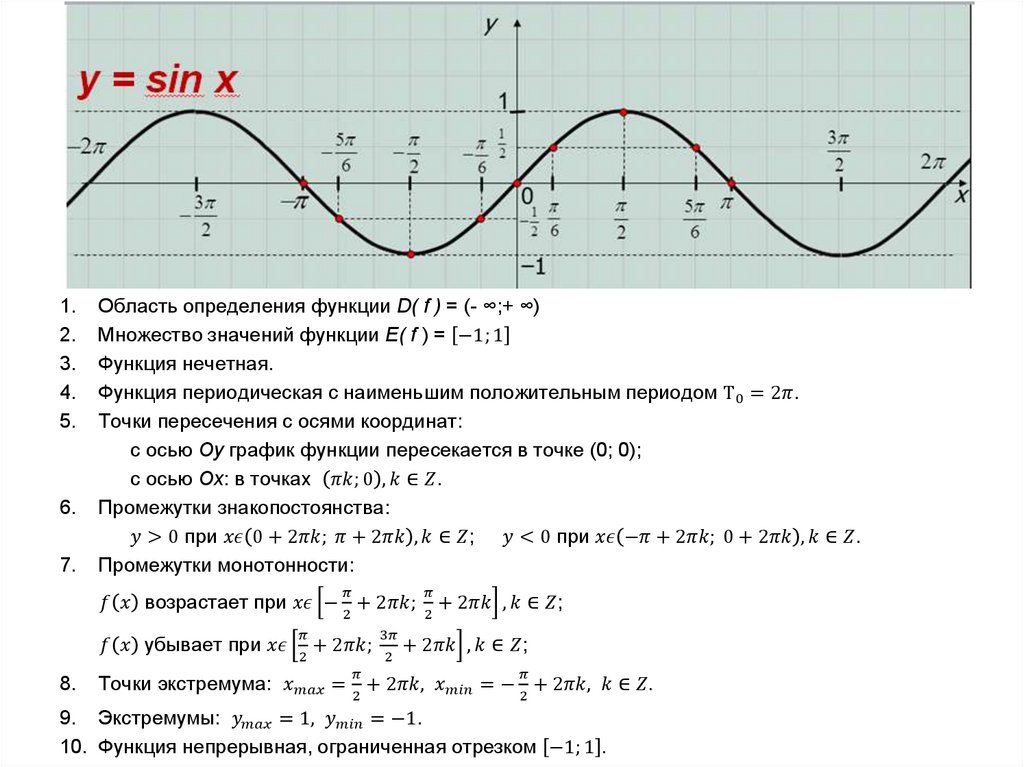
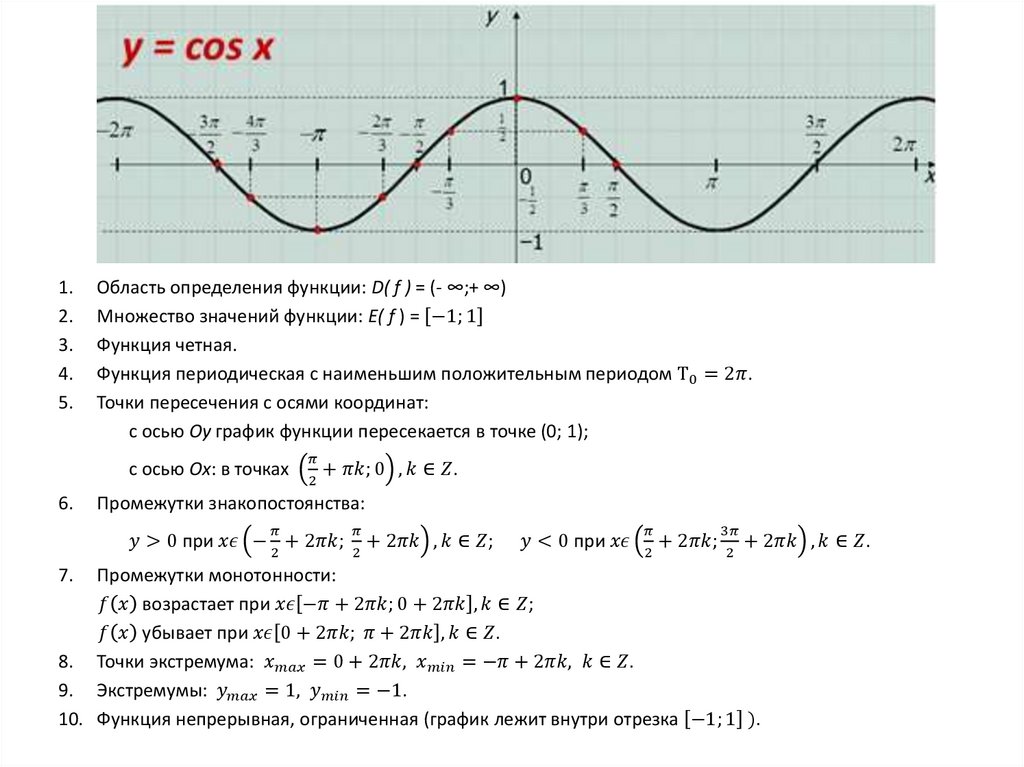
Область определения функции D( f ) = (- ∞;+ ∞)
Множество значений функции E( f ) = −1; 1
Функция нечетная.
Функция периодическая с наименьшим положительным периодом Т0 = 2