Similar presentations:
Свойства и графики функций y=sin(x) , y=cos(x)
1.
СВОЙСТВА ИГРАФИКИ ФУНКЦИЙ
Y=SIN(X) , Y=COS(X)
Выполнила : преподаватель математики
Рязанского станкостроительного колледжа
Л.В. Самойлова
2.
Математику, друзья,Не любить никак нельзя.
Очень строгая наука,
Очень точная наука –
Это математика!
3.
ОСНОВНЫЕ ЦЕЛИ ЗАНЯТИЯ:повторить пройденный материал по
тригонометрии;
познакомиться со свойствами функций y=sin(x),
y=cos(x);
научиться строить графики данных функций и
выполнять преобразования с ними;
развитие познавательного интереса у учащихся
к математике; повышение творческой
деятельности;
формирование навыков внимательности,
аккуратности и самостоятельности.
4.
ПЛАН ЗАНЯТИЯ:Организационный момент;
Повторение изученного материала и
проверка домашнего задания;
Объяснение нового материала;
Закрепление нового материала;
Подведение итогов и домашнее задание.
5.
КРОССВОРД1
3
п
5
7
с
9
13
ч
и
8
п
ё
2
о
а
т
р
а
г
н
у
г
м
р
т
а
а
д
н
и
г
а
е
н
н
с
е
р
и
о
д
6
н
ф
у
у
с
н
о
к
и
ц
д
и
а
я
п
р
р
и
о
в
м
е
е
д
ж
е
у
н
11
10
г
т
р
е
а
о
д
р
у
12
н
с
а
и
я
н
у
с
т
к
е
е
н
н
с
т
т
и
о
я
к
е
с
м
а
9.10.
6.
11.
COS(X)
ПРЕДЛОЖЕНИЕ,
МЕРА
ТРИГОНОМЕТРИЧЕСКИХ
ТРИГОНОМЕТРИЧЕСКАЯ
ТРЕБУЮЩЕЕ
ДОКАЗАТЕЛЬСТВА.
ФОРМУЛ.
………… CTG(X)
8.НАЗВАНИЕ
(0;
+
∞ФУНКЦИИ
)–ИЗМЕРЕНИЯ
–ЭТО
ЧТО
ЭТО
? УГЛА.
4.
КАКОЙ
НЕДОСТАЕТ:
SIN(X),
COS(X),
12.
НАЗВАНИЕ
ТРИГОНОМЕТРИЧЕСКОЙ
ФУНКЦИИ,
СООТВЕТСТВУЮЩЕЙ ОСИ ОРДИНАТ.
ОБРАТНАЯ
ФУНКЦИЯ
К ТАНГЕНСУ.
7.
КАК
НАЗЫВАЕТСЯ
ГРАФИК
ФУНКЦИИ
Y=SIN(X).
3.2.1.
13.
МЕРА
5.ОТ
ЗНАЧЕНИЕ
SIN(X)
ЧЕГО
ИЗМЕРЕНИЯ
ЗАВИСИТ
– НЕЧЕТНАЯ
ТРИГОНОМЕТРИЧЕСКИХ
УГЛА.
ЗНАЧЕНИЕ
ФУНКЦИЯ,
ТРИГОНОМЕТРИЧЕСКОЙ
А COS(X)
ФУНКЦИЙ
- ………….
ПОВТОРЯЕТСЯ
ФУНКЦИИ
ЧЕРЕЗ………….
6.
ПЛАН ИССЛЕДОВАНИЯТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
1.
2.
3.
4.
5.
6.
7.
8.
Область определения функции- D(y);
Область значений функции – E(y);
Четность / нечетность функции;
Наименьший положительный период;
Координаты точек пересечения графика функций с
осями: OX, OY;
Промежутки, на которых функция принимает
положительные и отрицательные значения;
Промежутки монотонности(возрастания и убывания)
функции;
Экстремумы: максимумы и минимумы функции.
7.
ГРАФИК И СВОЙСТВАФУНКЦИИ Y=SINX.
y
1
x
O
- 2П
-П
-1
П
2П
Свойства:
1. D(y) = R
6. Промежутки знакопостоянства:
2. E(y) = [ -1; 1]
sin x >0
при x є ( 0+2Пn; П+2Пn)
3. Нечетная функция: sin( - x)= - sin x;
sin x <0
при x є ( - П+2Пn; 0+2Пn)
график – синусоида, симметричен
7. Промежутки монотонности:
относительно начала координат
sin x ↑ при x є [ -П/2+2Пn; П/2+2Пn]
4. Периодичная функция:
sin x ↓ при x є [ П/2+2Пn; 3П/2+2Пn]
sin(x± 2Пn) = sin x , T=2П
5. Пересечение с осями: OX (0+Пn;0) 8. Экстремумы:
max: x= П/2+2Пn
y=1
OY (0;0)
min: x= -П/2+2Пn
y=-1
8.
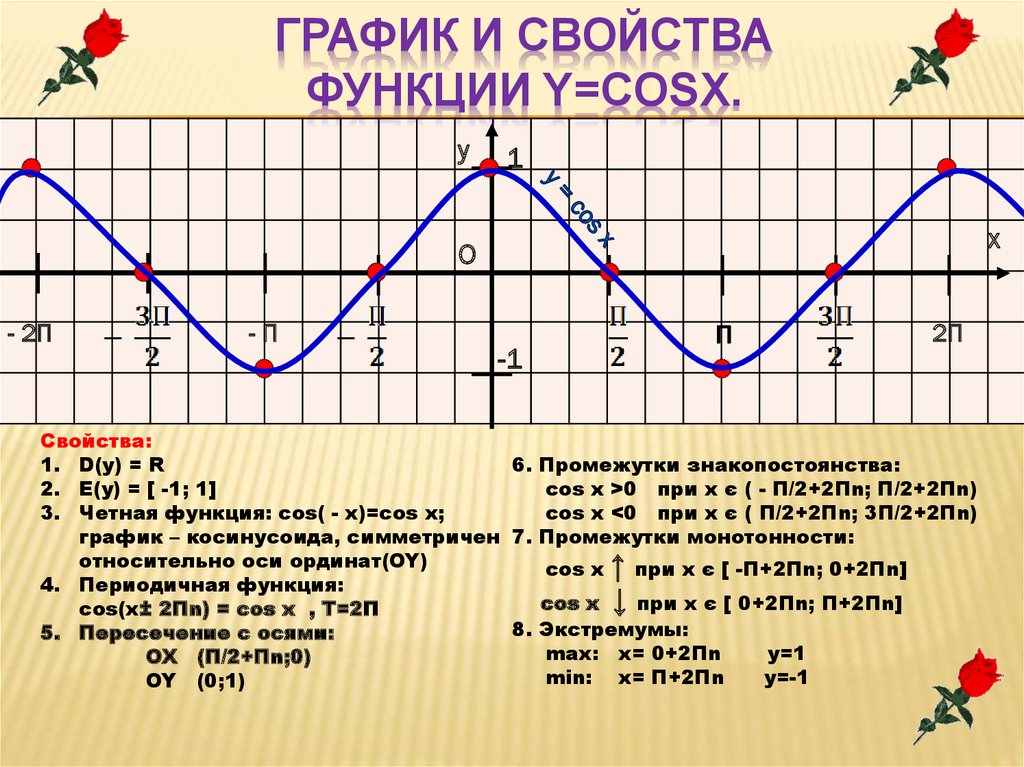
ГРАФИК И СВОЙСТВАФУНКЦИИ Y=COSX.
y
1
x
O
- 2П
-П
-1
П
2П
Свойства:
1. D(y) = R
6. Промежутки знакопостоянства:
2. E(y) = [ -1; 1]
cos x >0 при x є ( - П/2+2Пn; П/2+2Пn)
3. Четная функция: cos( - x)=cos x;
cos x <0 при x є ( П/2+2Пn; 3П/2+2Пn)
график – косинусоида, симметричен 7. Промежутки монотонности:
относительно оси ординат(OY)
cos x ↑ при x є [ -П+2Пn; 0+2Пn]
4. Периодичная функция:
cos x ↓ при x є [ 0+2Пn; П+2Пn]
cos(x± 2Пn) = cos x , T=2П
8. Экстремумы:
5. Пересечение с осями:
max: x= 0+2Пn
y=1
OX (П/2+Пn;0)
min: x= П+2Пn
y=-1
OY (0;1)
9.
ЗАДАНИЕ 1.y
2
1
x
O
- 2П
-П
-1
-2
Построить на одной координатной
плоскости следующие графики:
1. y= sin x
2. y= sin x + 1
3. y= 2 sin x
П
2П
10.
ЗАДАНИЕ 2.y
1
x
O
- 2П
-П
Построить на одной координатной
плоскости следующие графики:
П
-1
1. y= cos x
2. y= cos 2x
3. y= cos x/2
2П
11.
Построить на одной координатной плоскостиследующие графики:
1.
y= cos x
2.
y= cos x - 1
3.
y= ½ cos x










 mathematics
mathematics