Similar presentations:
Векторы в пространстве и действия над ними. Компланарные векторы. Тема 12
1.
2.
v• Многие физические
величины
характеризуются
числовым значением
и направлением в
пространстве, их
называют
векторными
величинами
F
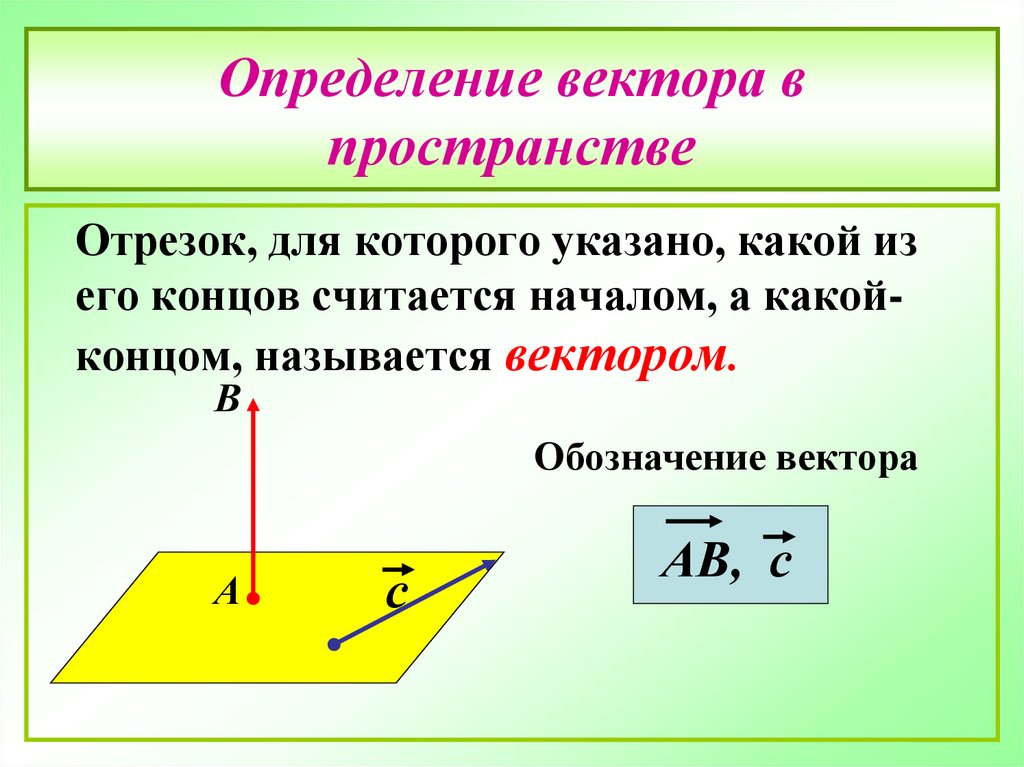
3. Определение вектора в пространстве
Отрезок, для которого указано, какой изего концов считается началом, а какойконцом, называется вектором.
В
Обозначение вектора
А
с
АВ, с
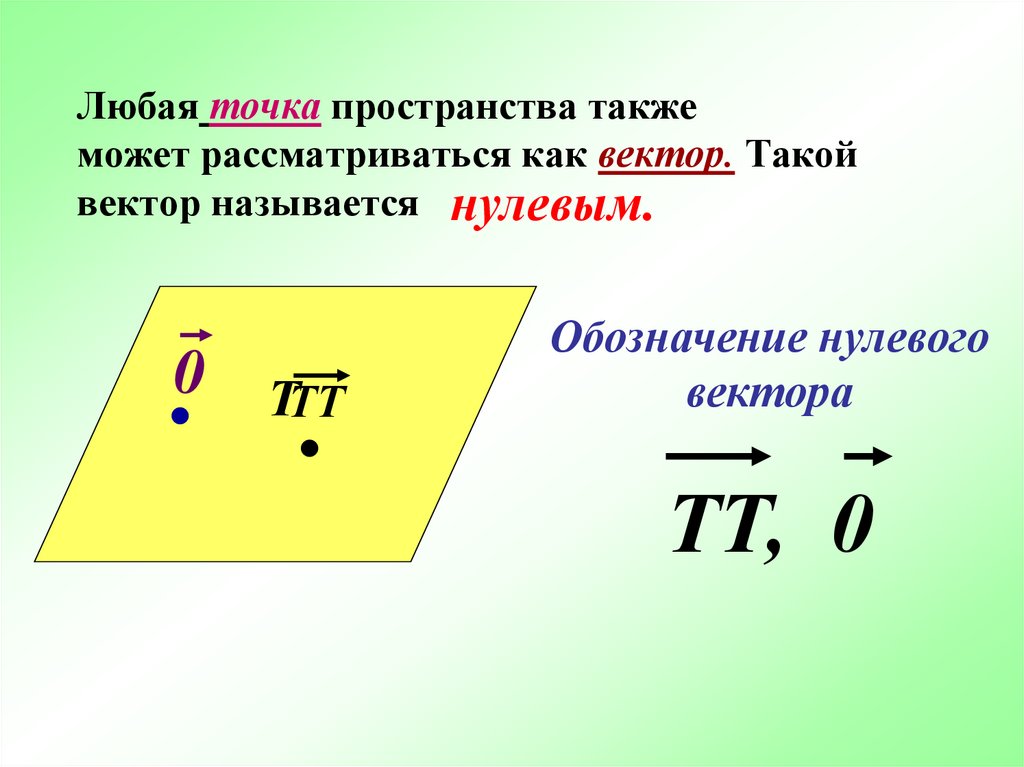
4. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется
нулевым.0 ТТТ
Обозначение нулевого
вектора
ТТ, 0
5. Длина ненулевого вектора
• Длиной вектора АВ называется длинаотрезка АВ.
• Длина вектора АВ (вектора а)
обозначается так:
АВ , а
• Длина нулевого вектора считается равной
нулю:
0 =0
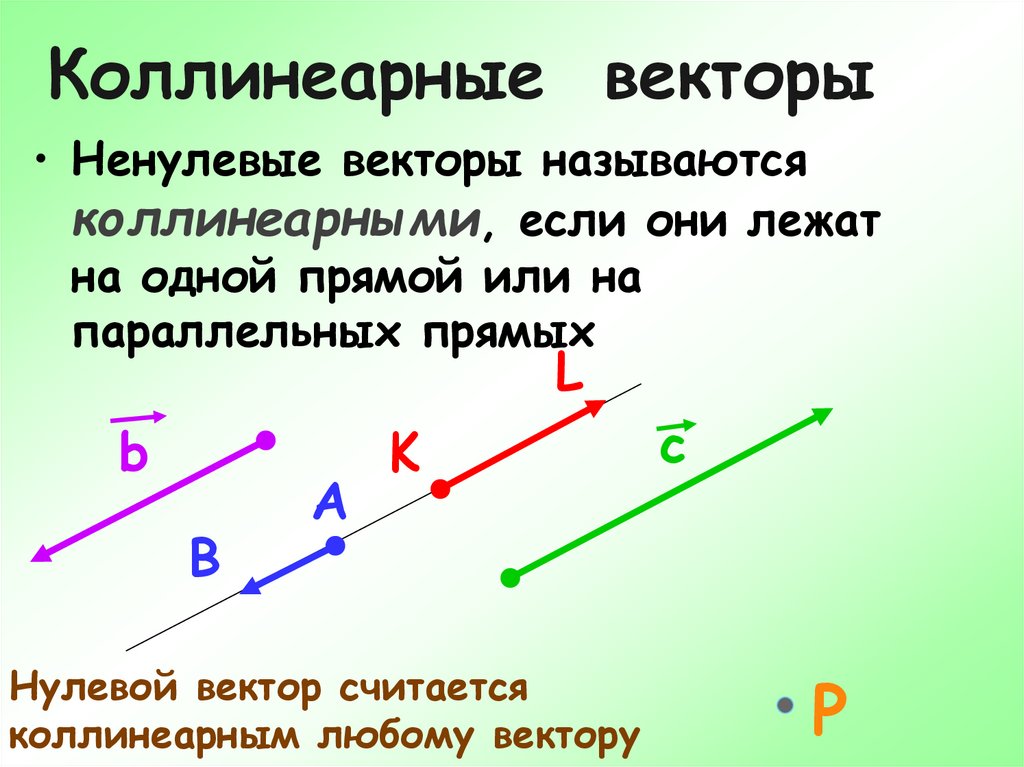
6. Коллинеарные векторы
• Ненулевые векторы называютсяколлинеарными, если они лежат
на одной прямой или на
параллельных прямых
L
b
B
A
K
Нулевой вектор считается
коллинеарным любому вектору
с
Р
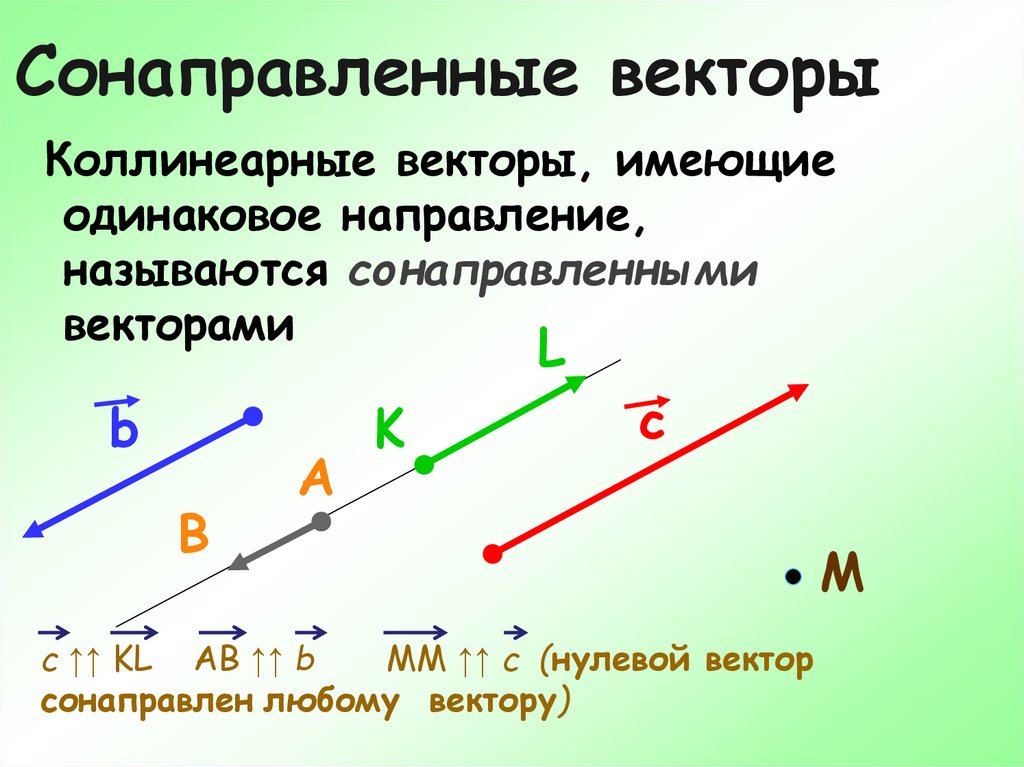
7. Сонаправленные векторы
Коллинеарные векторы, имеющиеодинаковое направление,
называются сонаправленными
векторами
L
b
B
A
K
с
c ↑↑ KL AB ↑↑ b
MM ↑↑ c (нулевой вектор
сонаправлен любому вектору)
М
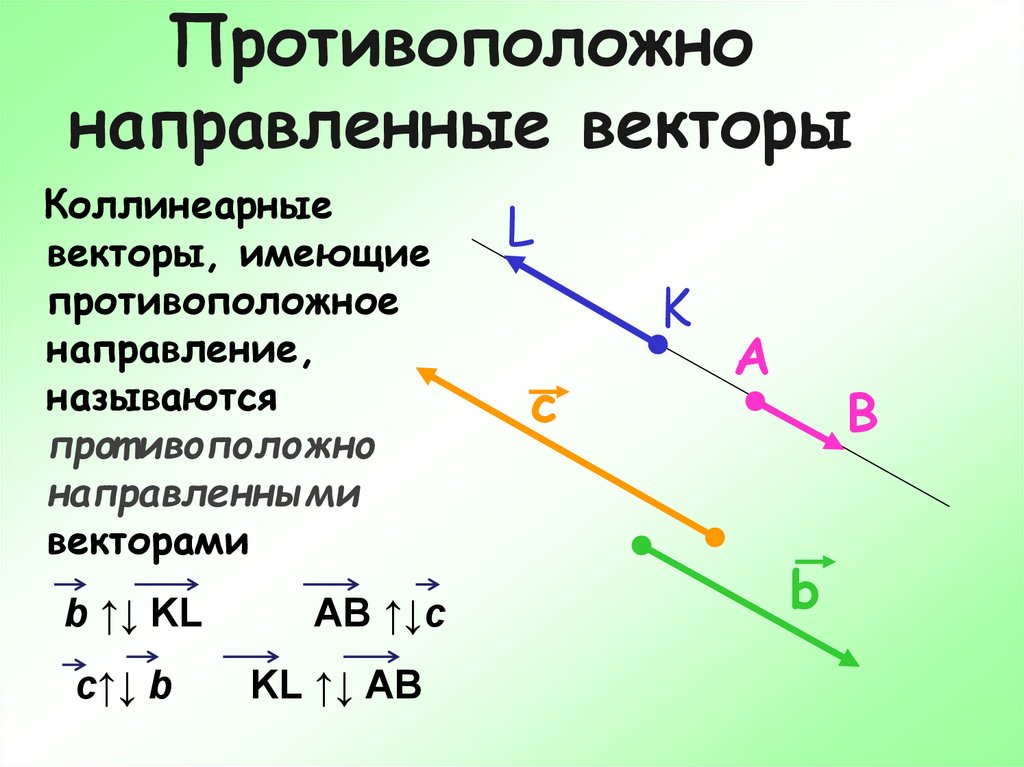
8. Противоположно направленные векторы
Коллинеарныевекторы, имеющие
противоположное
направление,
называются
прот ивоположно
направленными
векторами
b ↑↓ KL
c↑↓ b
AB ↑↓c
KL ↑↓ AB
L
K
с
A
B
b
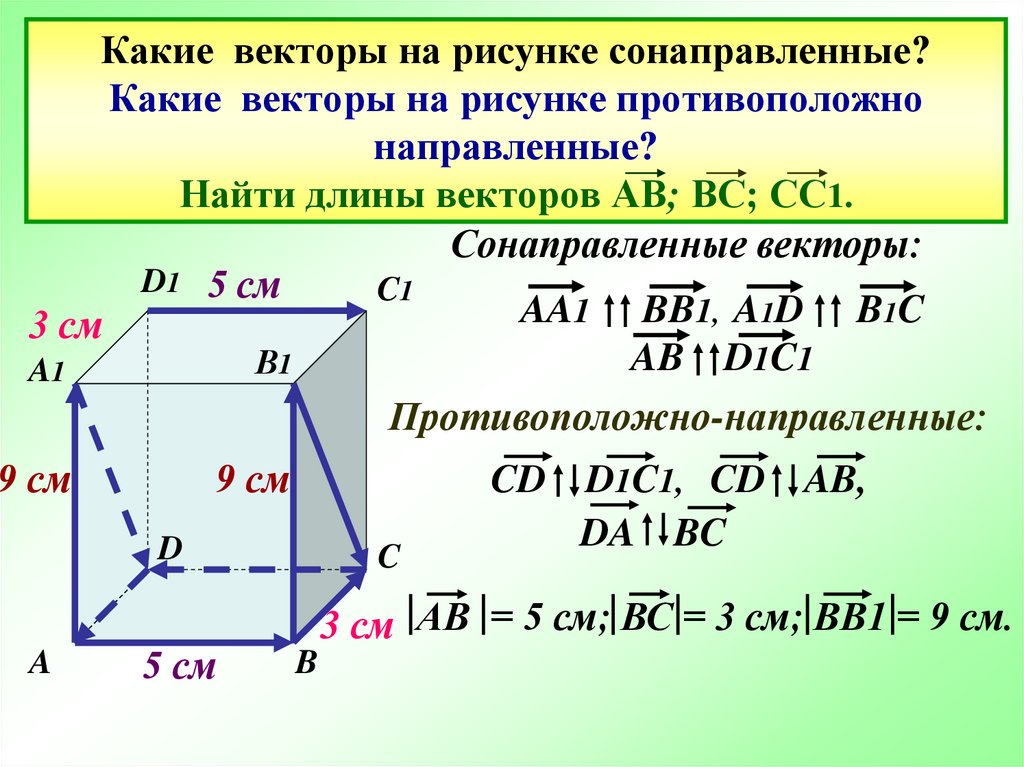
9. Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ; ВС;
СС1.Сонаправленные векторы:
D1 5 см
C1
AA1 BB1, A1D B1C
3 см
AB D1C1
В1
A1
Противоположно-направленные:
9 см
9 см
CD
D
A
5 см
C
D1C1, CD AB,
DA BC
3 см АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.
B
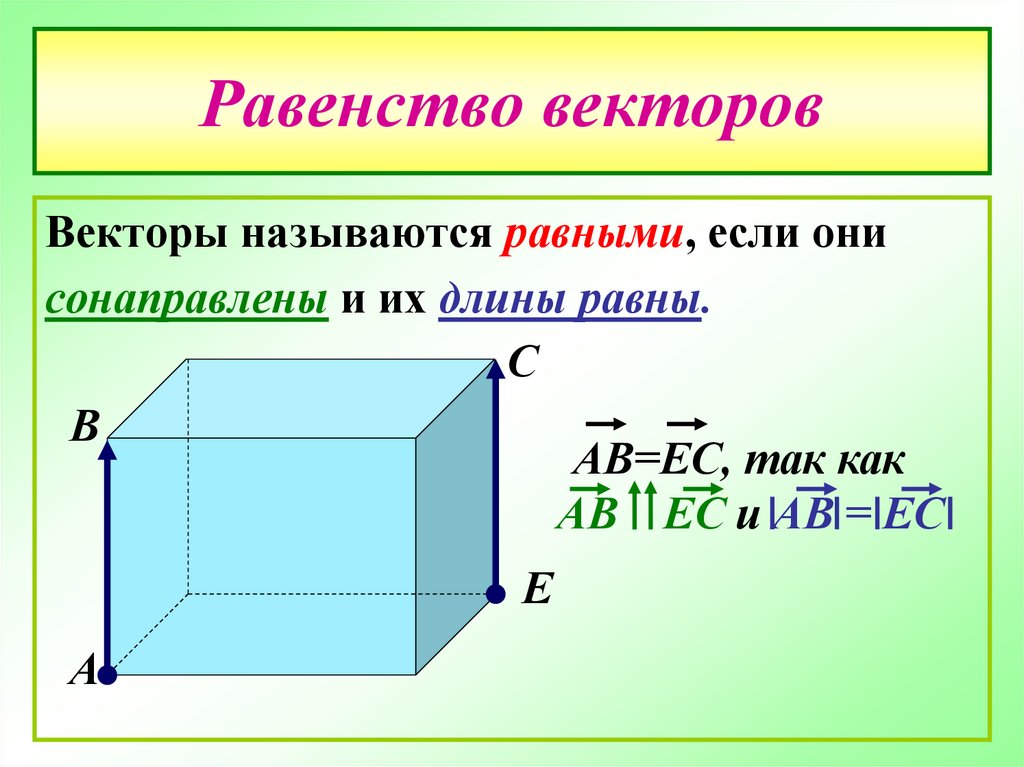
10. Равенство векторов
Векторы называются равными, если онисонаправлены и их длины равны.
С
В
АВ=ЕС, так как
АВ ЕС и АВ = ЕС
Е
А
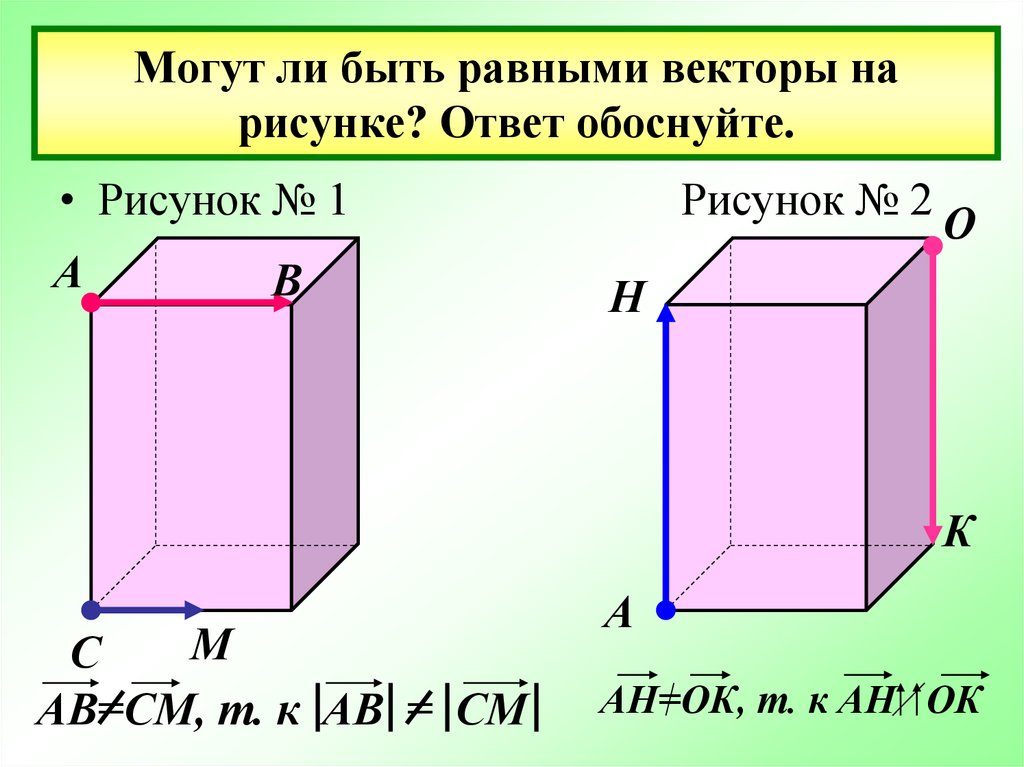
11. Могут ли быть равными векторы на рисунке? Ответ обоснуйте.
• Рисунок № 1А
В
Рисунок № 2
О
Н
К
М
С
АВ=СМ, т. к АВ = СМ
А
АН=ОК, т. к АН ОК
12. Доказать, что от любой точки пространства можно отложить вектор, равный данному, и притом только один
Дано: а, М.Доказать: в = а, М в, единственный.
Э
М
а
Проведем через вектор а и точку
М плоскость.
В этой плоскости построим
МК = а.
Из теоремы о параллельности
прямых следует МК = а и М МК.
Э
К
Доказательство:
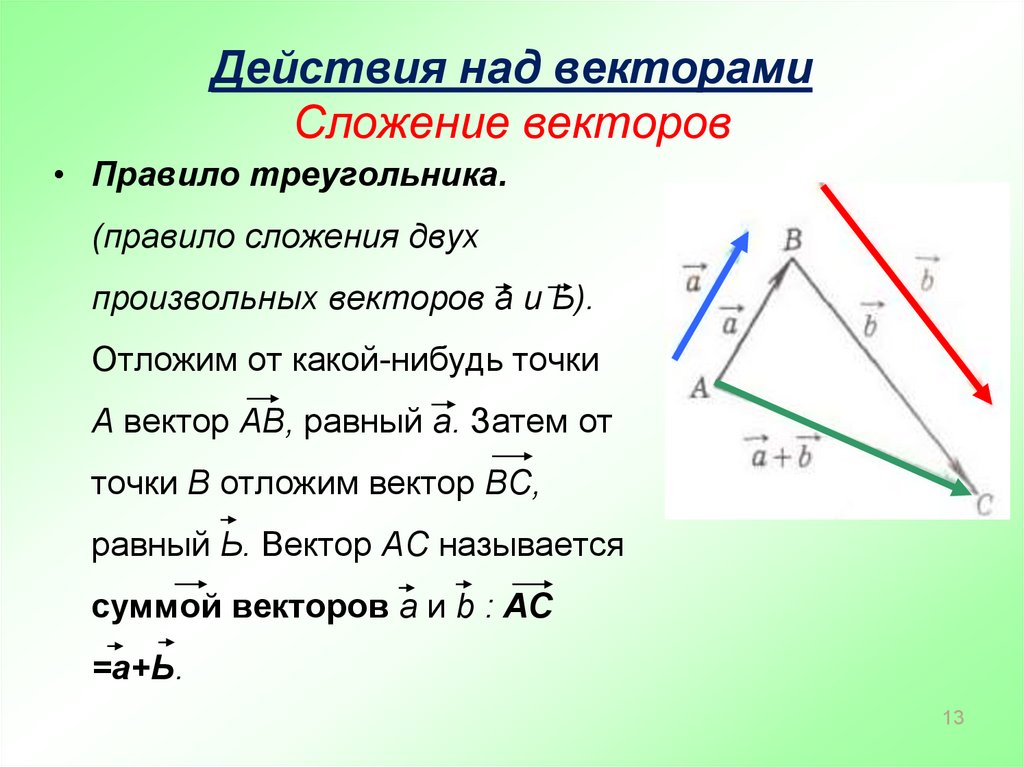
13. Действия над векторами Сложение векторов
• Правило треугольника.(правило сложения двух
произвольных векторов а и Ь).
Отложим от какой-нибудь точки
А вектор АВ, равный а. Затем от
точки В отложим вектор ВС,
равный Ь. Вектор АС называется
суммой векторов а и b : АС
=а+Ь.
13
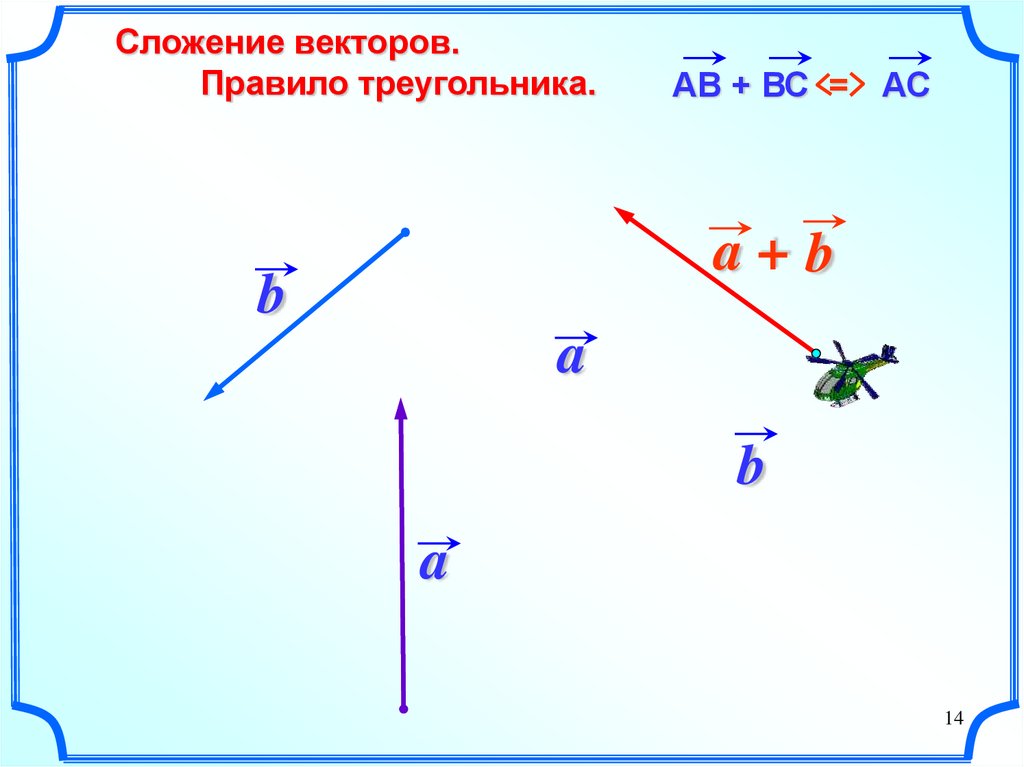
14.
Сложение векторов.Правило треугольника.
АВ + ВС = АС
a+b
b
a
b
a
14
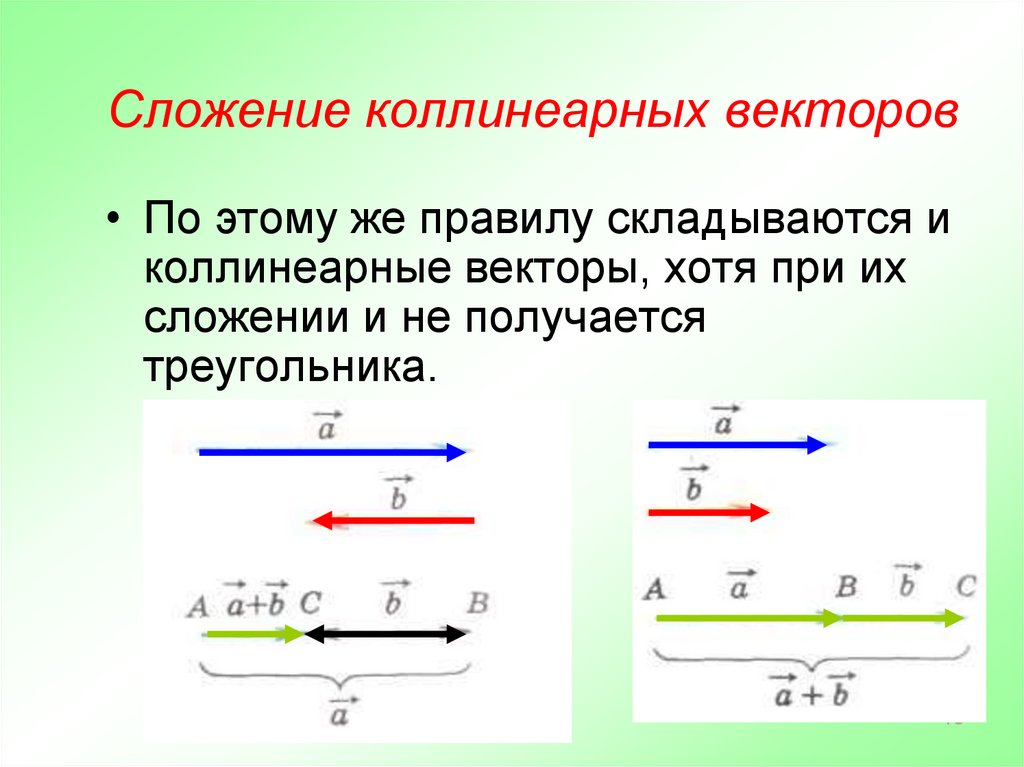
15. Сложение коллинеарных векторов
• По этому же правилу складываются иколлинеарные векторы, хотя при их
сложении и не получается
треугольника.
15
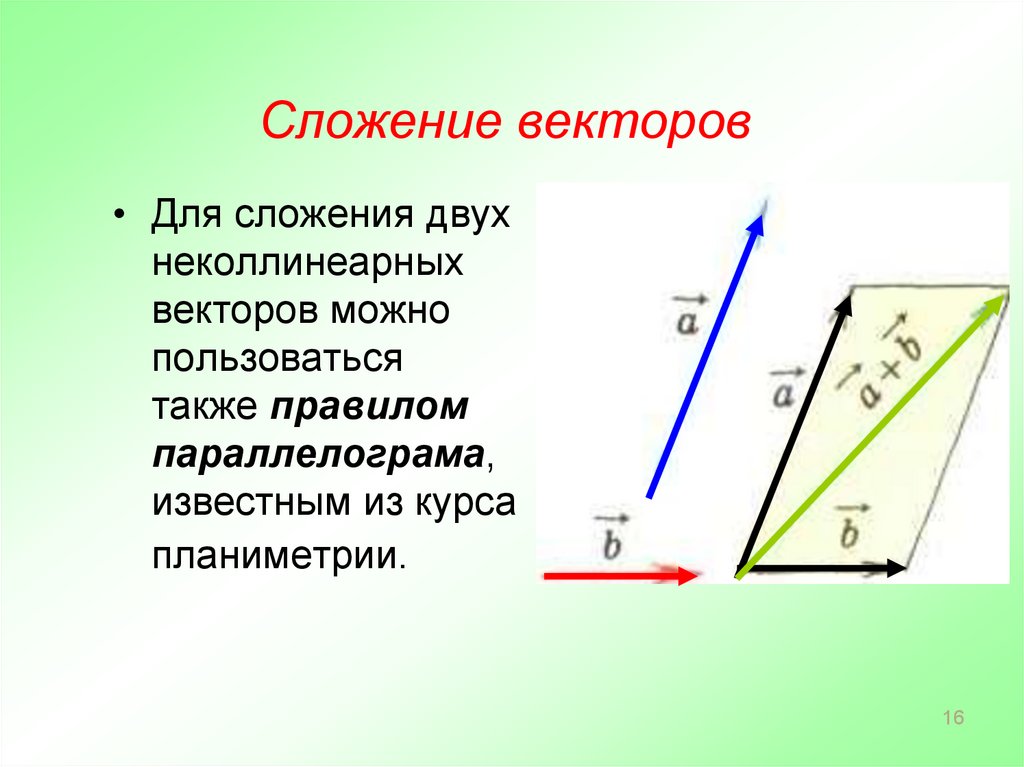
16. Сложение векторов
• Для сложения двухнеколлинеарных
векторов можно
пользоваться
также правилом
параллелограма,
известным из курса
планиметрии.
16
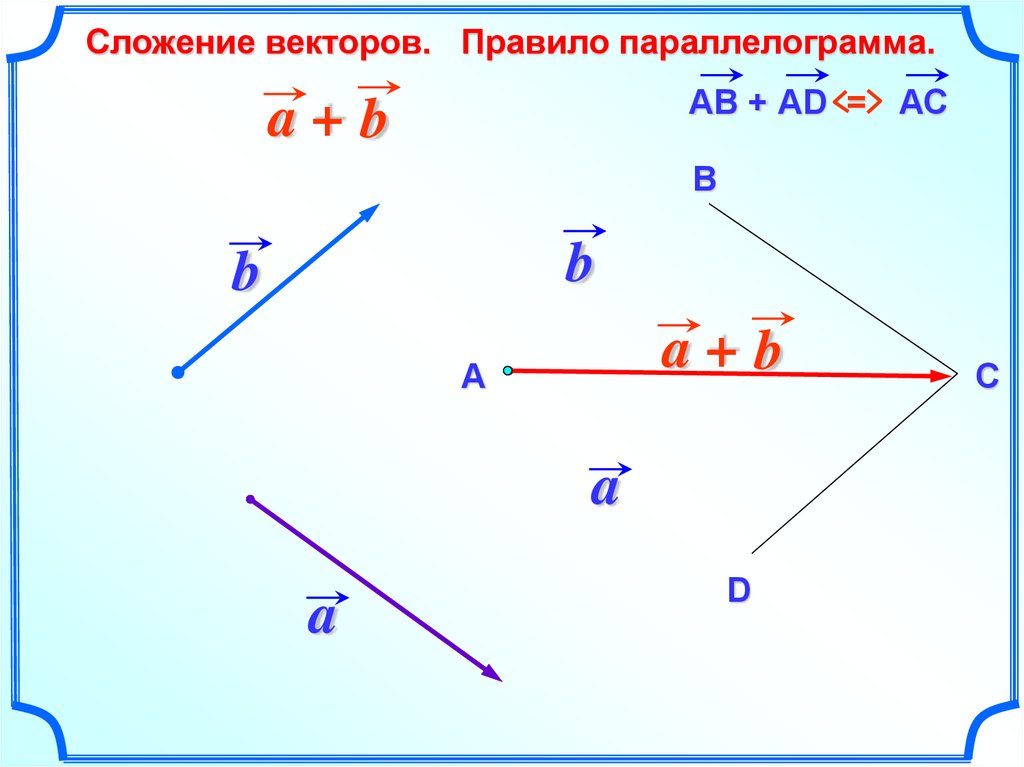
17.
Сложение векторов. Правило параллелограмма.АВ + АD = АС
a+b
В
b
b
a+b
А
a
a
D
C
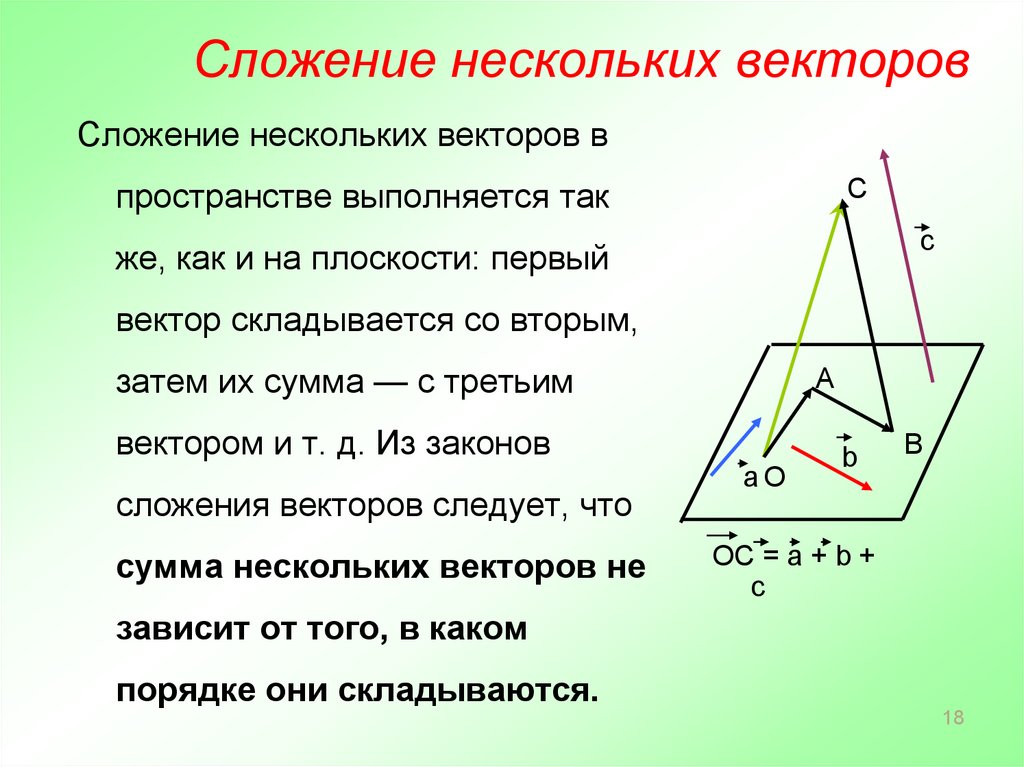
18. Сложение нескольких векторов
Сложение нескольких векторов вС
пространстве выполняется так
с
же, как и на плоскости: первый
вектор складывается со вторым,
затем их сумма — с третьим
вектором и т. д. Из законов
сложения векторов следует, что
сумма нескольких векторов не
А
аО
b
В
ОС = a + b +
c
зависит от того, в каком
порядке они складываются.
18
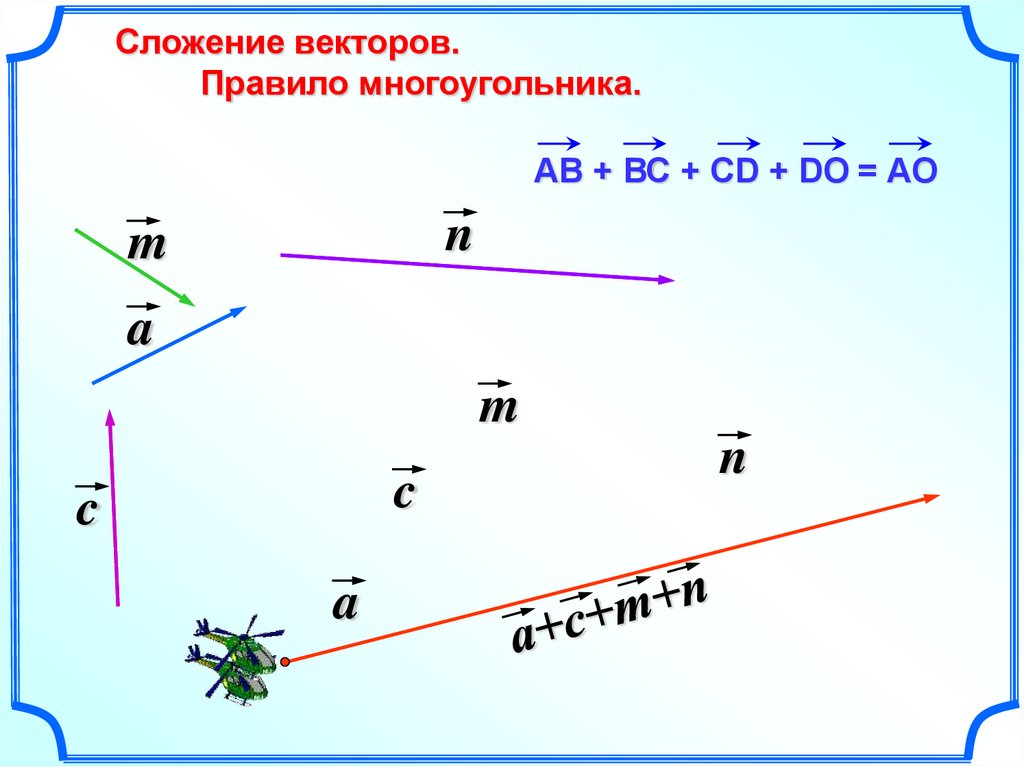
19.
Сложение векторов.Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
20.
Свойства сложения векторовДля любых векторов справедливы
равенства:
a+b=b+a (переместительный закон)
(a+b)+c=a+ (b+c) (сочетательный закон)
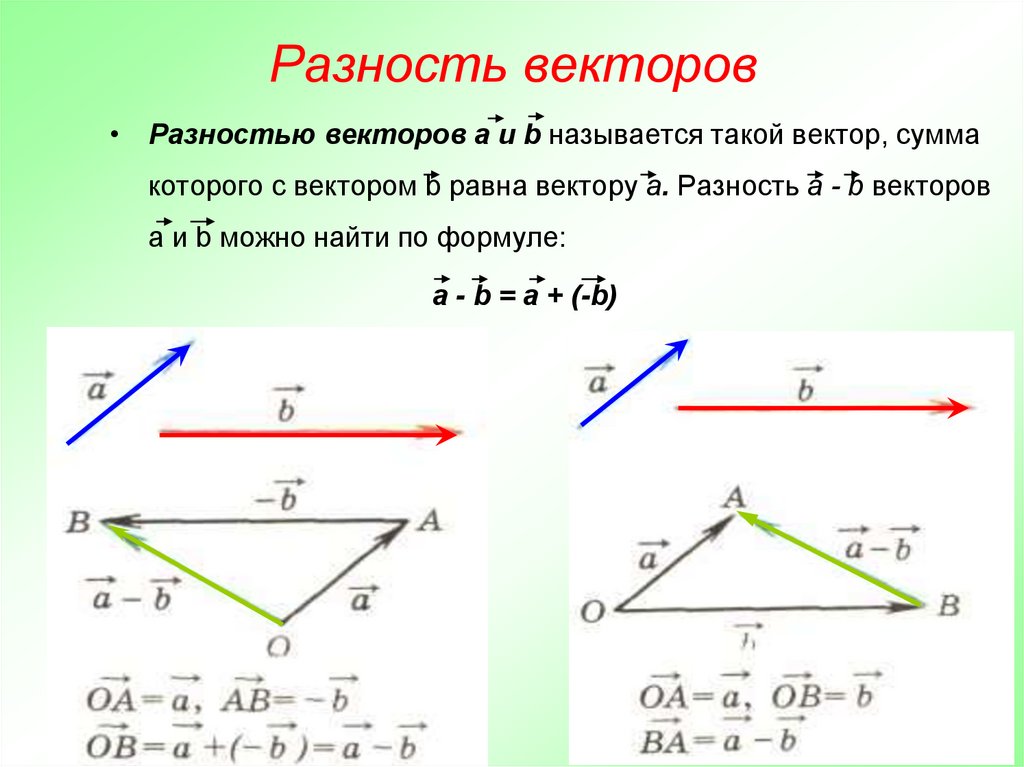
21. Разность векторов
• Разностью векторов а и b называется такой вектор, суммакоторого с вектором b равна вектору а. Разность а - b векторов
а и b можно найти по формуле:
а - b = а + (-b)
21
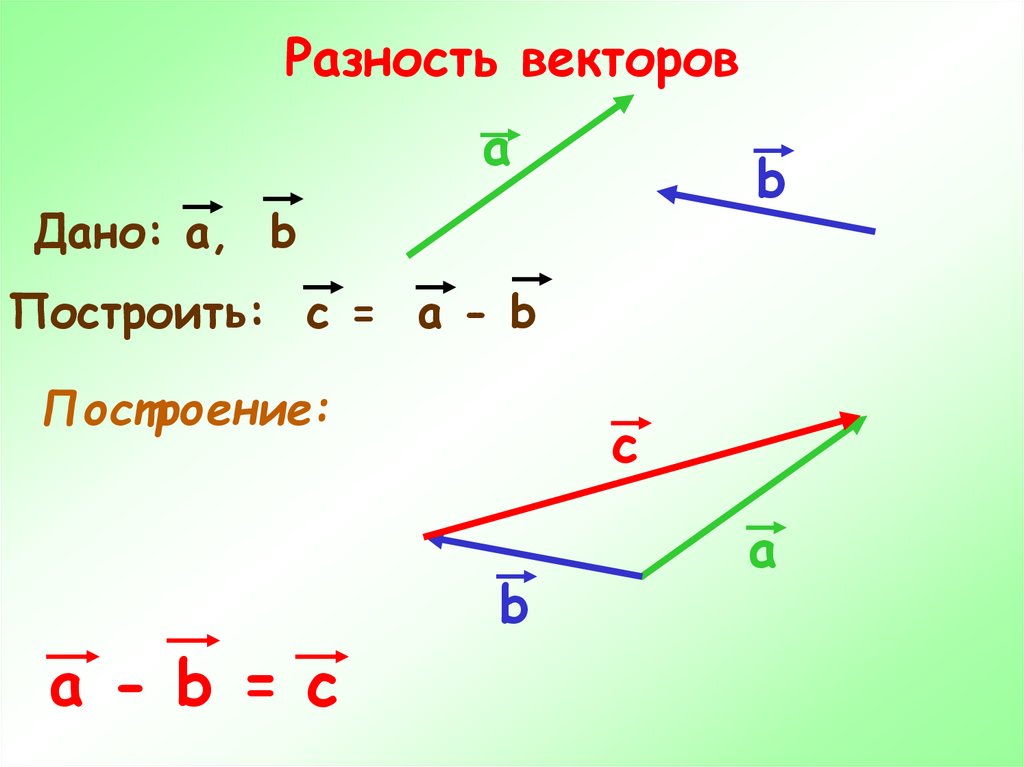
22.
Разность векторовa
b
Дано: a, b
Построить: c = a - b
Построение:
a - b = c
с
b
a
23. Умножение вектора a на число k
k·a = b,|a| ≠ 0, k – произвольное число
|b| = |k|·|a|,
2a
если k>0, то a ↑↑ b
a
если k<0, то a ↑↓ b
-2a
Для любых чисел k, l и любых векторов a, b справедливы равенства:
1º. (kl)a= k(la) (сочетательный закон),
2º. (k+l)a= ka+la (первый распределительный закон),
3º. k(a+b) = ka+kb (второй распределительный закон).
24.
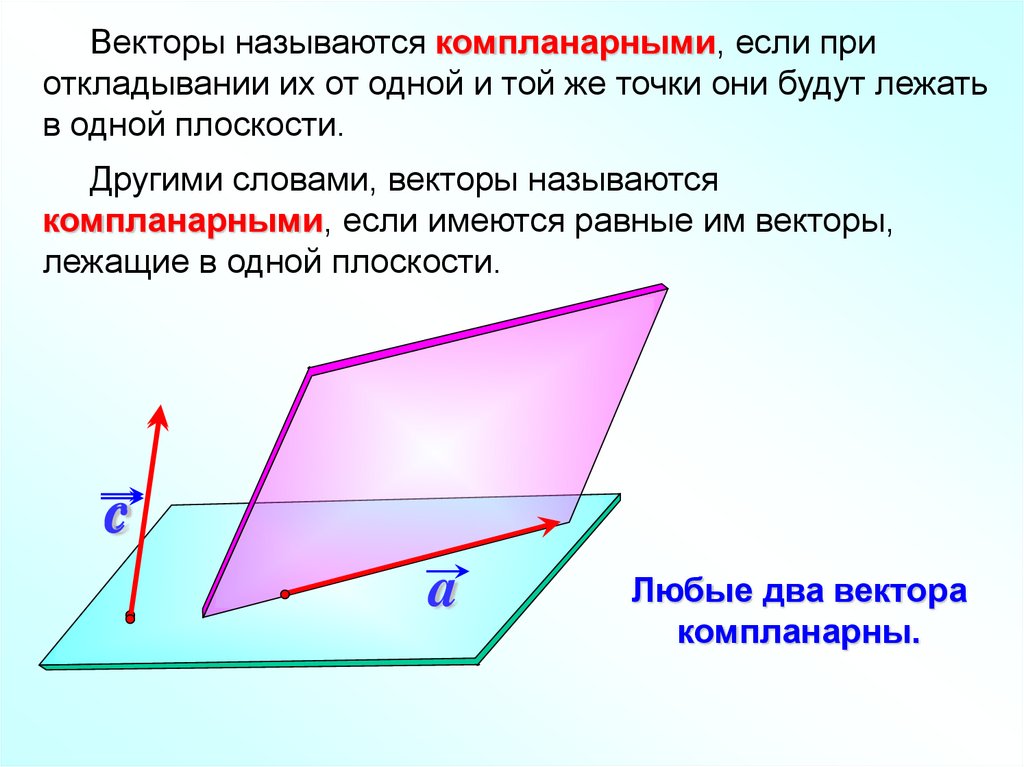
Векторы называются компланарными, если приоткладывании их от одной и той же точки они будут лежать
в одной плоскости.
Другими словами, векторы называются
компланарными, если имеются равные им векторы,
лежащие в одной плоскости.
c
a
Любые два вектора
компланарны.
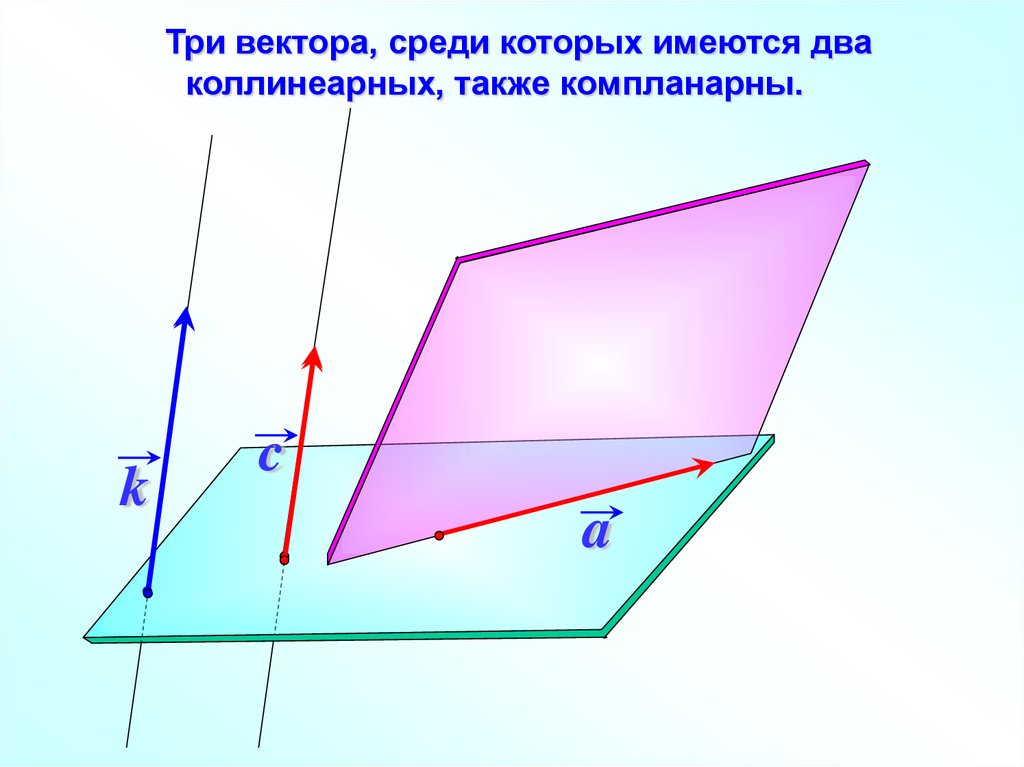
25.
Три вектора, среди которых имеются дваколлинеарных, также компланарны.
k
c
a
26.
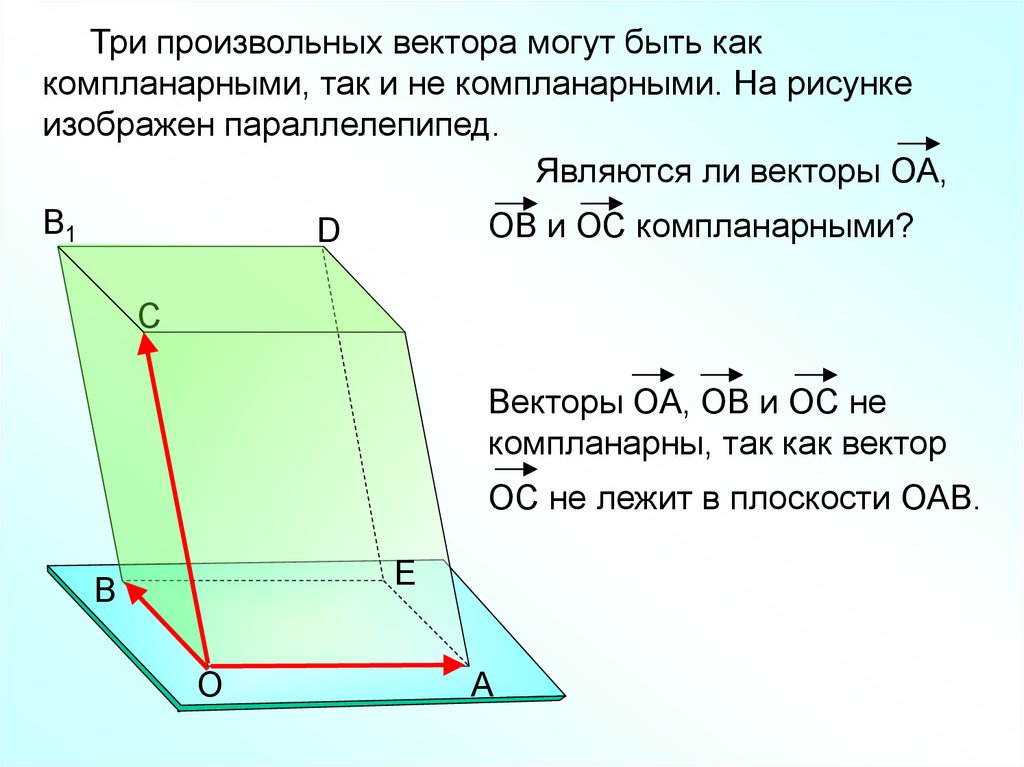
Три произвольных вектора могут быть каккомпланарными, так и не компланарными. На рисунке
изображен параллелепипед.
Являются ли векторы ОА,
B1
ОВ и ОС компланарными?
D
C
Векторы ОА, ОВ и ОС не
компланарны, так как вектор
ОС не лежит в плоскости ОАВ.
Е
В
О
А
27.
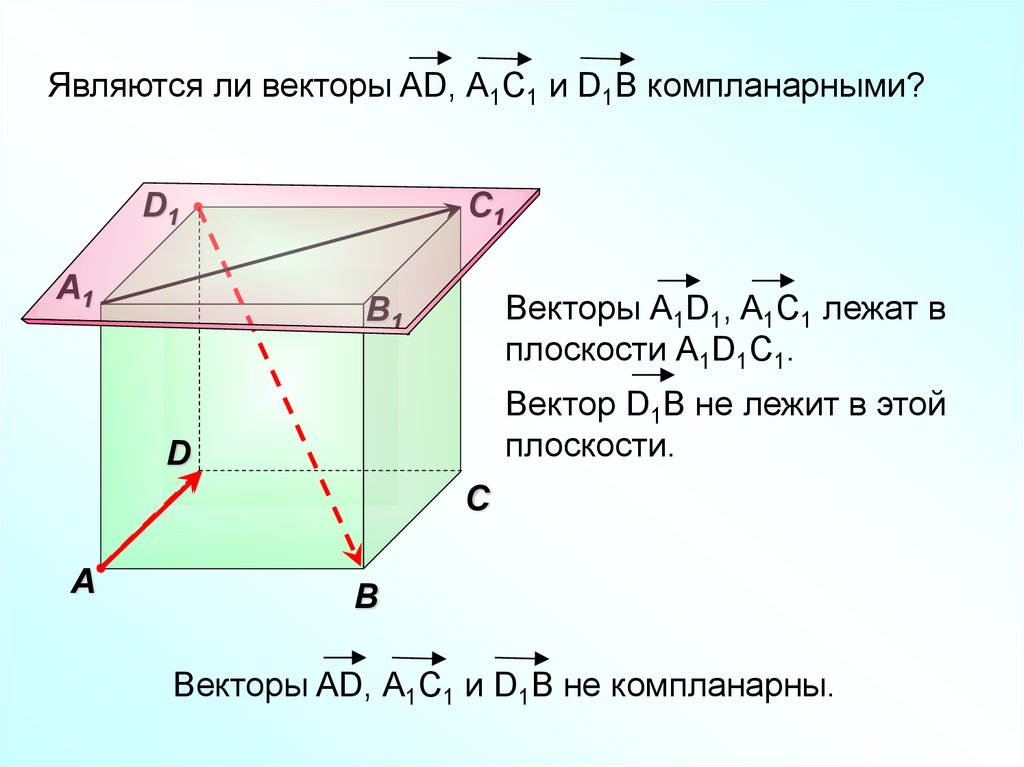
Являются ли векторы AD, А1С1 и D1B компланарными?D1
A1
C1
Векторы А1D1, A1C1 лежат в
плоскости А1D1C1.
B1
Вектор D1В не лежит в этой
плоскости.
D
C
A
B
Векторы AD, А1С1 и D1B не компланарны.
28.
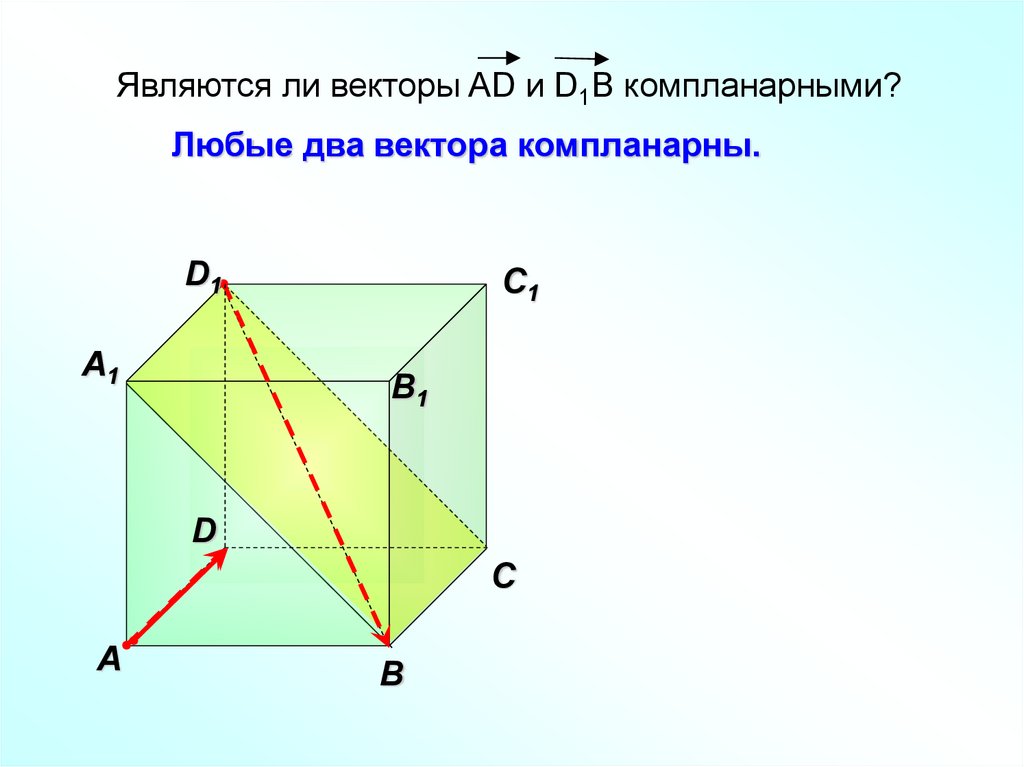
Являются ли векторы AD и D1B компланарными?Любые два вектора компланарны.
D1
A1
C1
B1
D
C
A
B
29.
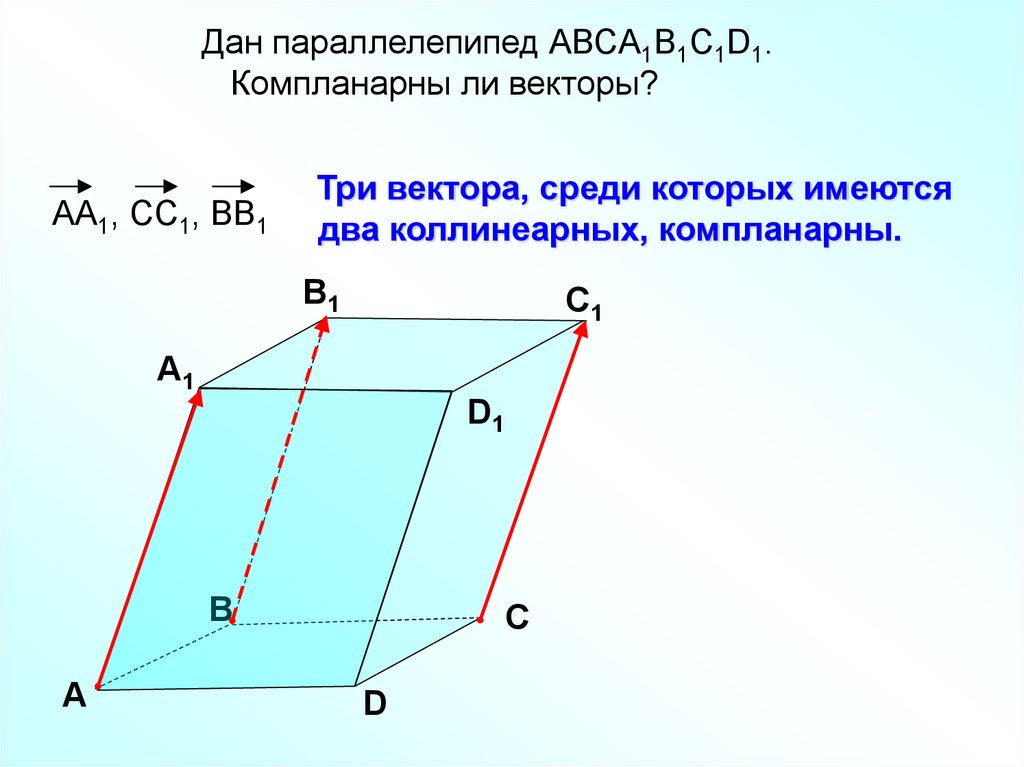
Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
АА1, СС1, ВВ1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
В1
С1
А1
D1
В
А
С
D
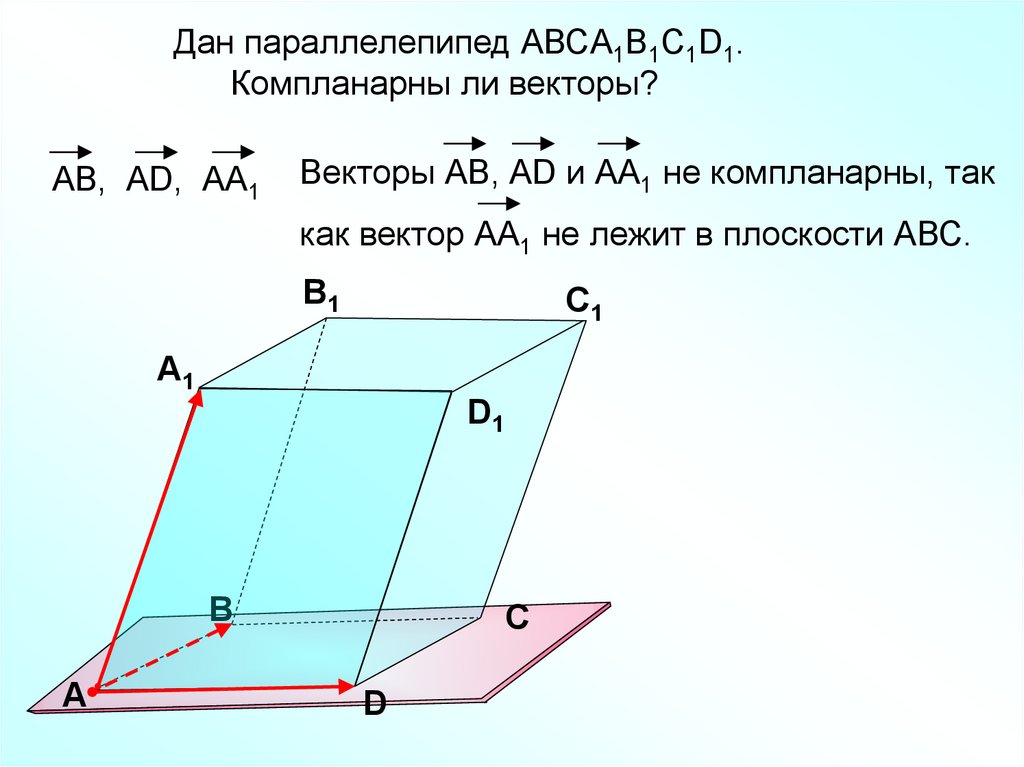
30.
Дан параллелепипед АВСA1B1C1D1.Компланарны ли векторы?
АВ, АD, АА1
Векторы АВ, АD и АА1 не компланарны, так
как вектор АА1 не лежит в плоскости АВС.
В1
С1
А1
D1
В
А
С
D
31.
Признак компланарностиЕсли вектор
a
c
можно разложить по векторам
c = xa + yb
где x и y – некоторые числа, то векторы a, b и c
и
b
, т.е. представить в виде
компланарны.
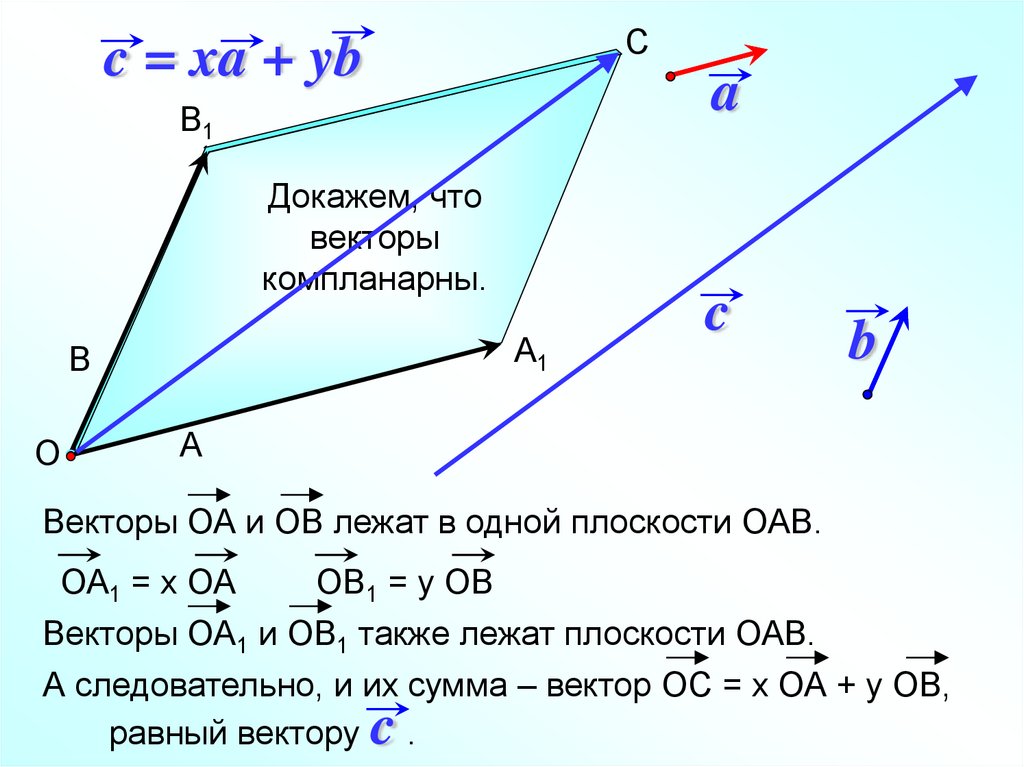
32.
Сc = xa + yb
a
В1
Докажем, что
векторы
компланарны.
А1
В
О
c
b
А
Векторы ОА и ОВ лежат в одной плоскости ОАВ.
ОА1 = х ОА
ОВ1 = у ОВ
Векторы ОА1 и ОВ1 также лежат плоскости ОАВ.
А следовательно, и их сумма – вектор ОС = х ОА + у ОВ,
равный вектору .
c
33.
Справедливо и обратное утверждение.Если векторы
a
и
b
a, b и c
компланарны, а векторы
не коллинеарны, то вектор
a
b
c = xa + yb
разложить по векторам
c можно
и
, причем
коэффициенты разложения определяются
единственным образом.
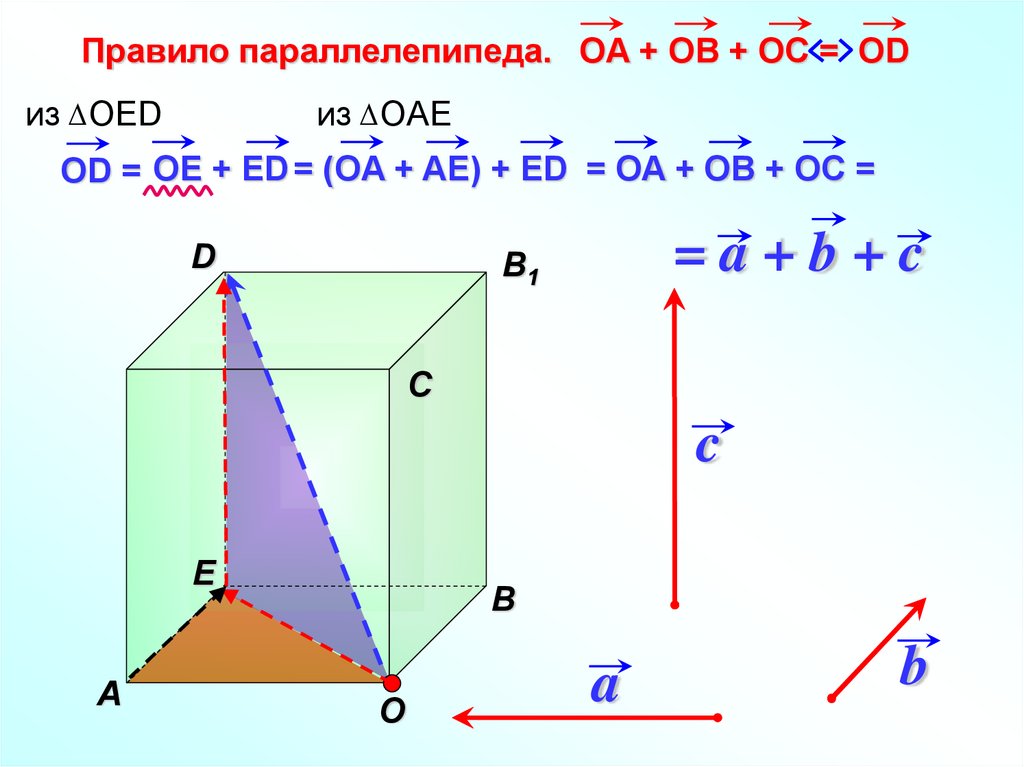
34.
Правило параллелепипеда. OA + OB + OC = ODиз OED
из OAE
OD = OE + ED = (OA + AE) + ED = OA + OB + OC =
D
=a+b+c
В1
С
c
Е
A
В
О
a
b
35.
Разложение вектора по трем некомпланарнымвекторам. Если вектор представлен в виде
p = xa + yb + zc
z - некоторые числа, то говорят, что вектор p
разложен по векторам a , b и c . Числа x , y и z
где
x, y
и
называются коэффициентами разложения.
Теорема о разложении вектора по трем
некомпланарным векорам.
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
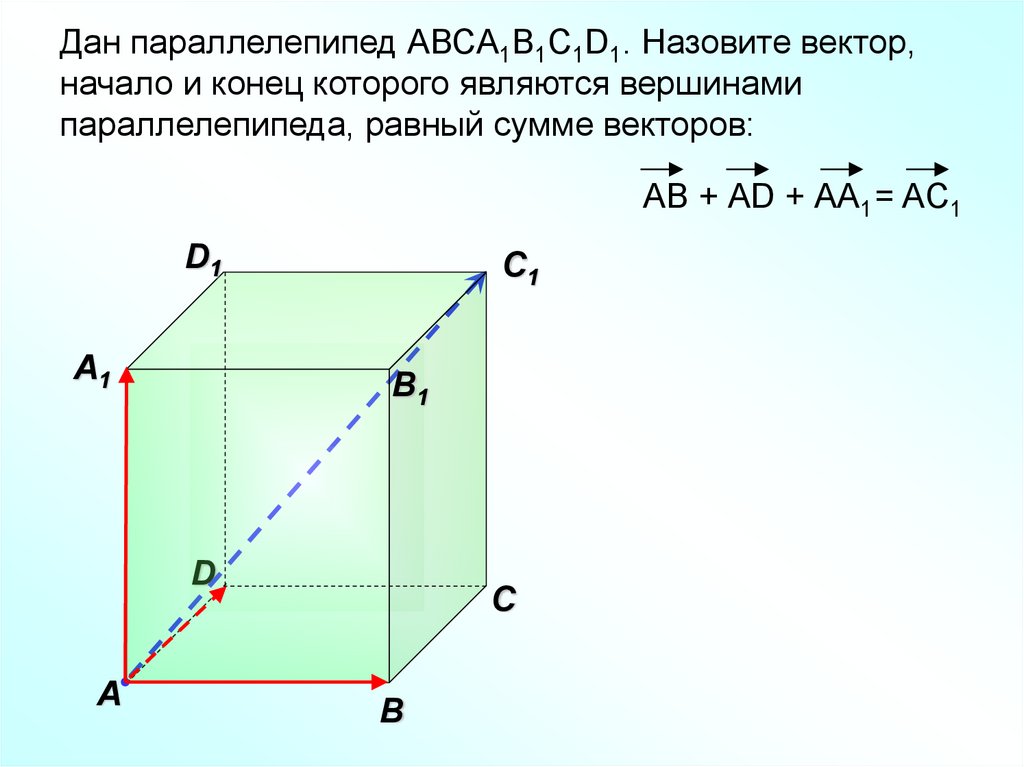
36.
Дан параллелепипед АВСA1B1C1D1. Назовите вектор,начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
АВ + АD + АА1 = AC1
D1
A1
C1
B1
D
A
С
В
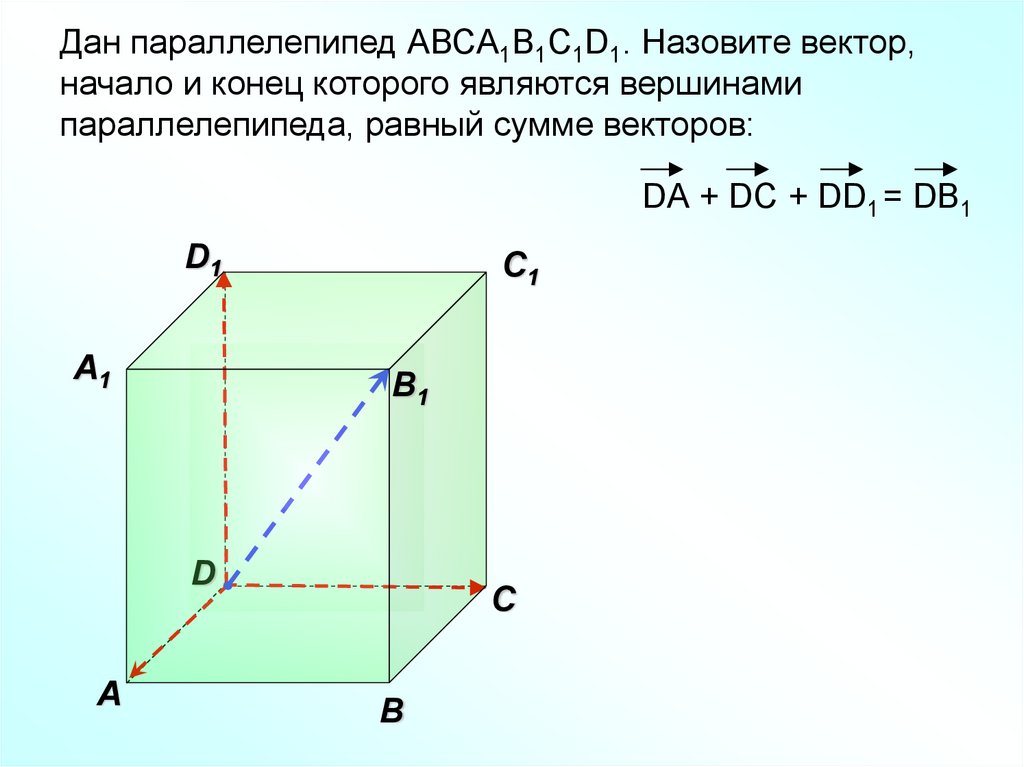
37.
Дан параллелепипед АВСA1B1C1D1. Назовите вектор,начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
DА + DC + DD1 = DB1
D1
A1
C1
B1
D
A
С
В
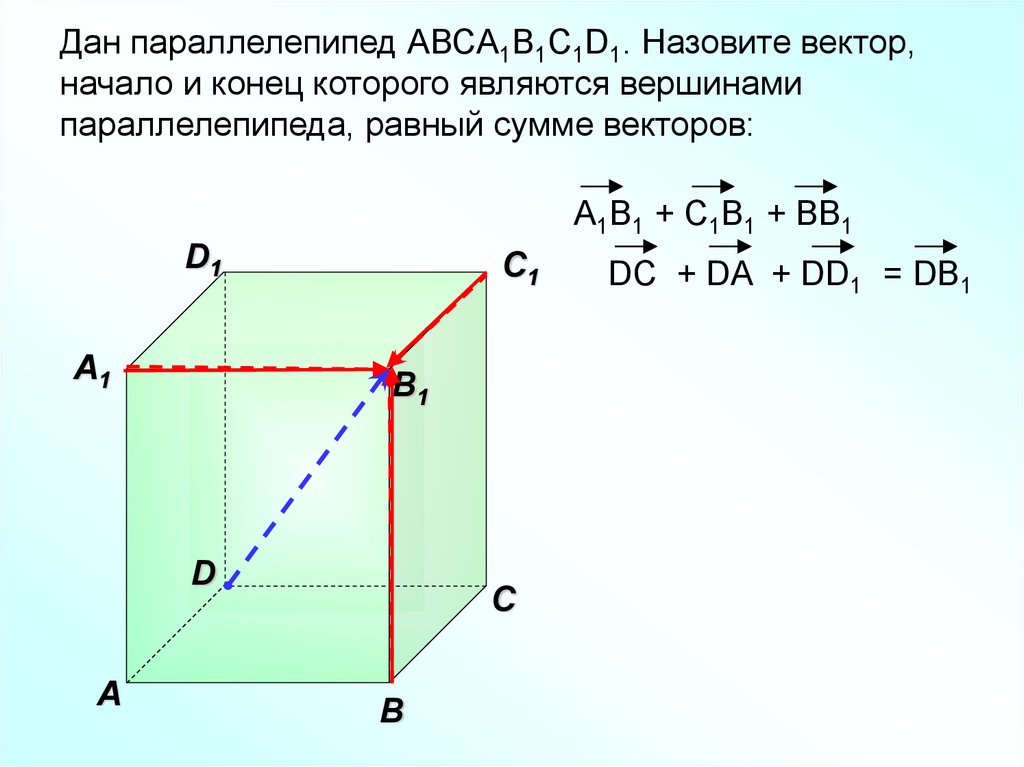
38.
Дан параллелепипед АВСA1B1C1D1. Назовите вектор,начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
A1B1 + C1B1 + BB1
D1
A1
C1
B1
D
A
С
В
DC + DA + DD1 = DB1
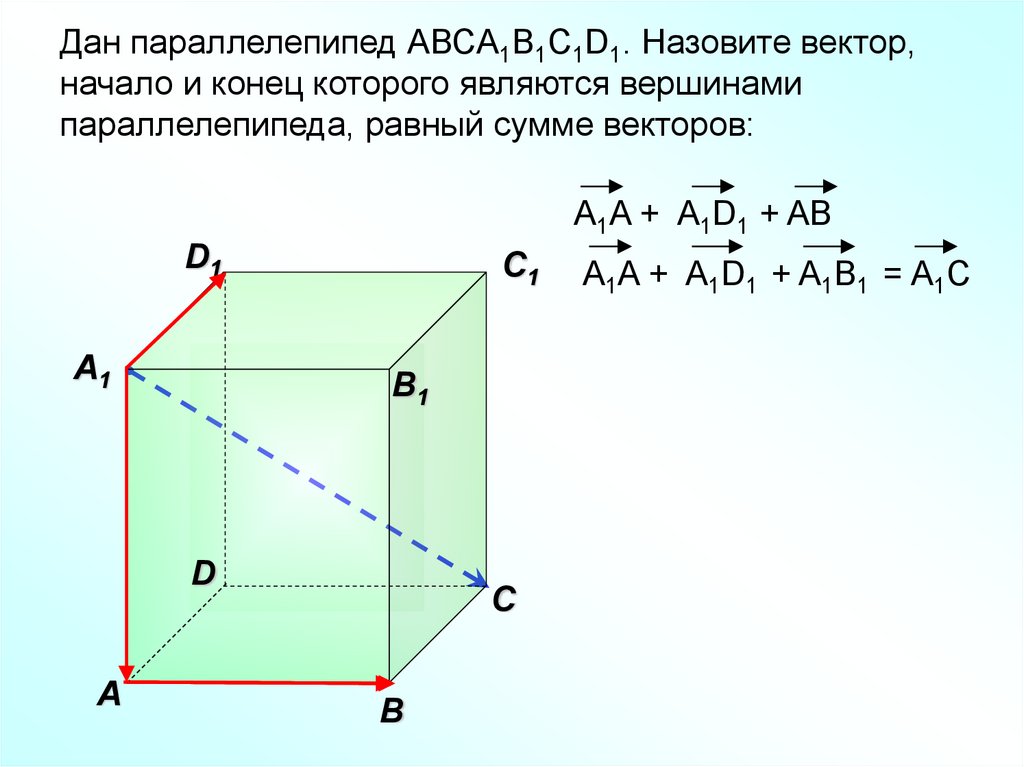
39.
Дан параллелепипед АВСA1B1C1D1. Назовите вектор,начало и конец которого являются вершинами
параллелепипеда, равный сумме векторов:
A1A + A1D1 + AB
D1
A1
C1
B1
D
A
С
В
A1A + A1D1 + A1B1 = A1C








 mathematics
mathematics








