Similar presentations:
Векторы. Смешанное произведение векторов
1. Векторы
2. Смешанное произведение векторов.
• Смешанным произведением векторов a, b и cназывается число, равное скалярному
произведению вектора a b на вектор c
Обозначение:
a b c
a b c
a, b, c
3. Геометрически:
Смешанное произведение трехвекторов
равно
объему
параллелепипеда, построенного
на этих векторах, взятому со
знаком «+», если эти векторы
образуют правую тройку, и со
знаком «-», если они образуют
левую тройку.
a b
c
H
b
a
a b c a b pr
a b
c S H V
4. Свойства смешанного произведения.
1)a b c b c a c a b
или
a b c b c a c a b
смешанное произведение не меняется при циклической
перестановке векторов.
2)
a b c a b c
смешанное произведение не меняется при перестановке
знаков векторного и скалярного умножения
5.
3) a b c a c b b a c c b aсмешанное произведение меняет свой знак на
противоположный при перемене мест любых двух
векторов-сомножителей.
4) a b c 0 a, b, c
компланарны
6.
Смешанное произведение векторов, заданныхсвоими координатами.
a ax i a y j az k
ax
ay
az
b bx i by j bz k
a b c bx
by
bz
cx
cy
cz
c cx i c y j cz k
Смешанное
произведение
векторов
равно
определителю третьего порядка, составленному из
координат перемножаемых векторов.
7.
Доказательство:a b c
ay
by
az
bz
i
i
j
k
ax
ay
a z cx i c y j cz k
bx
by
bz
ax
az
bx
bz
j
ax
bx
k cx i c y j cz k
by
ay
8.
ayaz
by
bz
cx
ax
az
bx
bz
cy
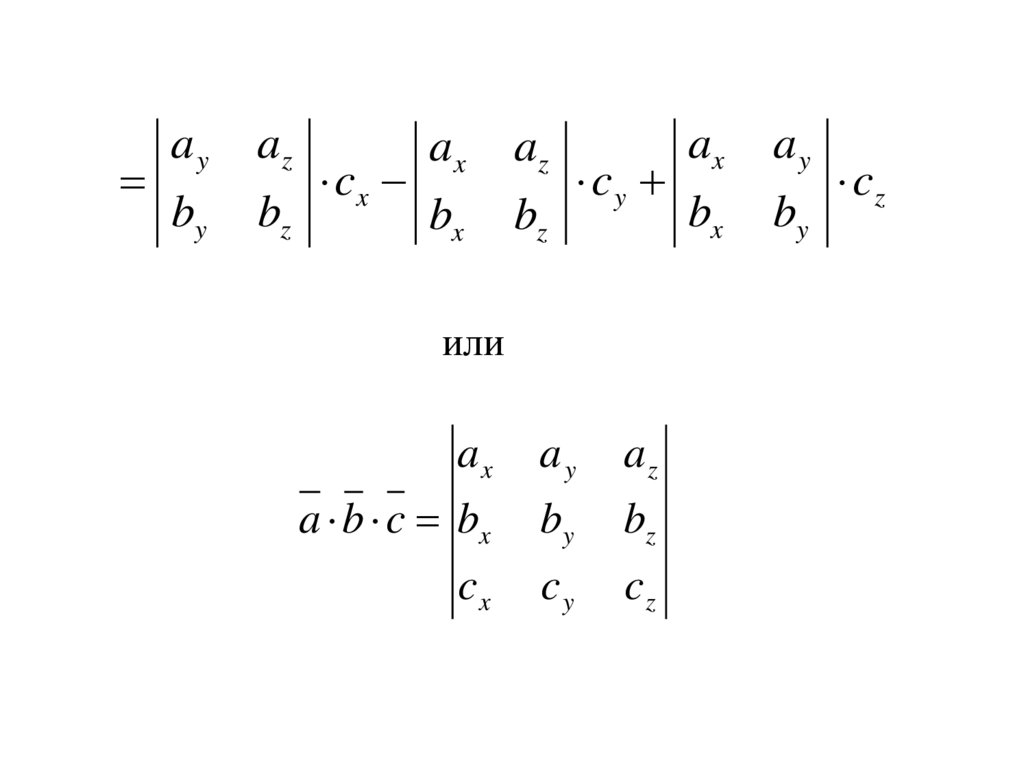
или
ax
ay
az
a b c bx
by
bz
cx
cy
cz
ax
ay
bx
by
cz
9.
Некоторые приложения смешанногопроизведения.
• компланарность векторов:
a b c 0
ax
ay
az
bx
by
bz 0 a, b, c
cx
cy
cz
компланарны
10.
• определение взаимной ориентации векторов впространстве:
a b c 0 , mo a, b, c
- правая тройка
a b c 0 , mo a, b, c
- левая тройка
11.
• определениеобъемов
треугольной пирамиды:
параллелепипеда
c
c
b
b
a
a
Vпар-да
a b c
1
Vпир a b c
6
и
12.
Пример 1. Доказать, что точки А(5;7;-2), В(3;1;-1),С(9;4;-4), D(1;5;0) лежат в одной плоскости.
Решение.
Покажем, что векторы AB, AC , AD
лежат в одной плоскости, т.е. компланарны.
AB 2; 6; 1 AC 4; 3; 2
В
С
А
AD 4; 2; 2
D
2 6
AB AC AD 4
1
3 2 0
4 2
2
Векторы компланарны,
следовательно точки А,
В, С и D лежат в одной
плоскости.
13.
Пример 2.Найти объем пирамиды и длину высоты,
опущенной на грань BCD, если даны координаты вершин
пирамиды: А(0;0;1), В(2;3;5), С(6;2;3), D(3;7;2)
А
Решение.
С
BA 2; 3; 4 BD 1; 4; 3
BC 4; 1; 2
В
2 3 4
1
1
V BA BD BC 1
6
6
4
4
3 20
1 2
Н
D
14.
1V S OCH H
3
i
j
BD BC 1
4
3V
H
S OCH
S OCH
1
BD BC
2
k
3 11 i 10 j 17 k
4 1 2
BD BC 112 10 2 17 2 510
S OCH
3 V 3 20 2 120
H
S OCH
510
510
510
2
Ответ.
V=20
(ед3)
,
120
H
510













 mathematics
mathematics








