Similar presentations:
Векторное произведение векторов
1. Векторное произведение векторов
2.
Векторным произведением вектора aна вектор b наз. вектор c a b,
удовлетворяющий следующим условиям:
1)
c a b sin
2) c
a
c
b
3)векторы образуют правую тройку
3. Понятие «правой» тройки векторов
a, b , cТройку векторов
называют правой, если
направление вектора c таково, что, смотря из его конца
вдоль вектора, кратчайший поворот от вектора
a
к вектору b будет виден против движения часовой
стрелки.
с
b
a, b, с - правая тройка
a
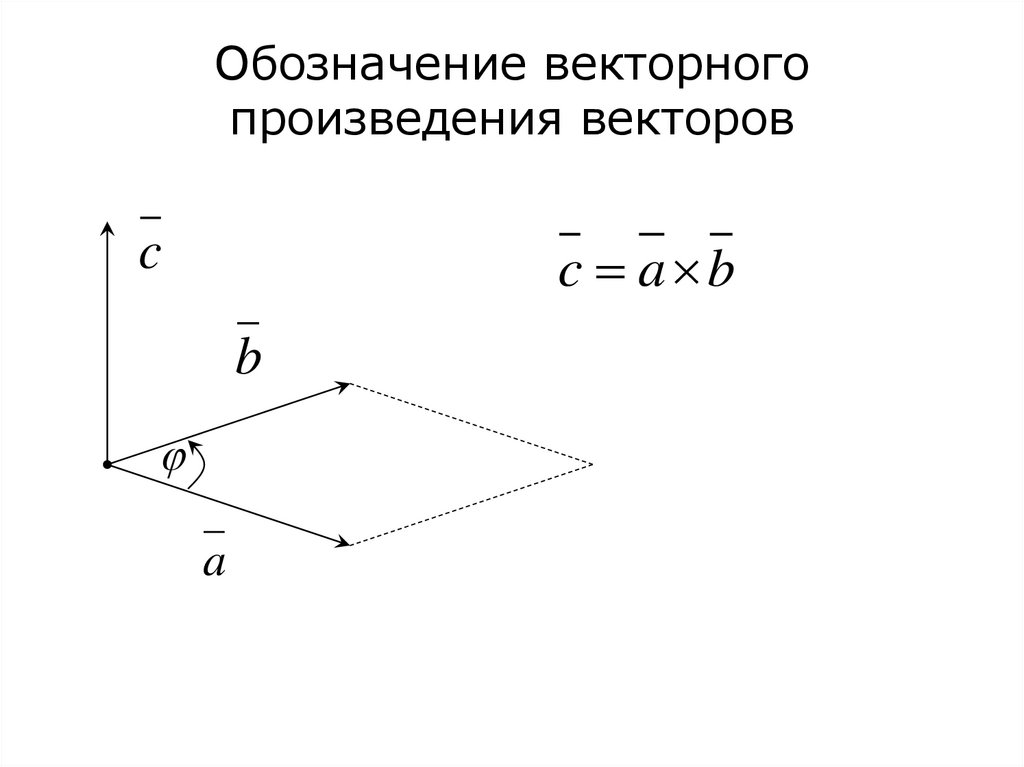
4. Обозначение векторного произведения векторов
cc a b
b
a
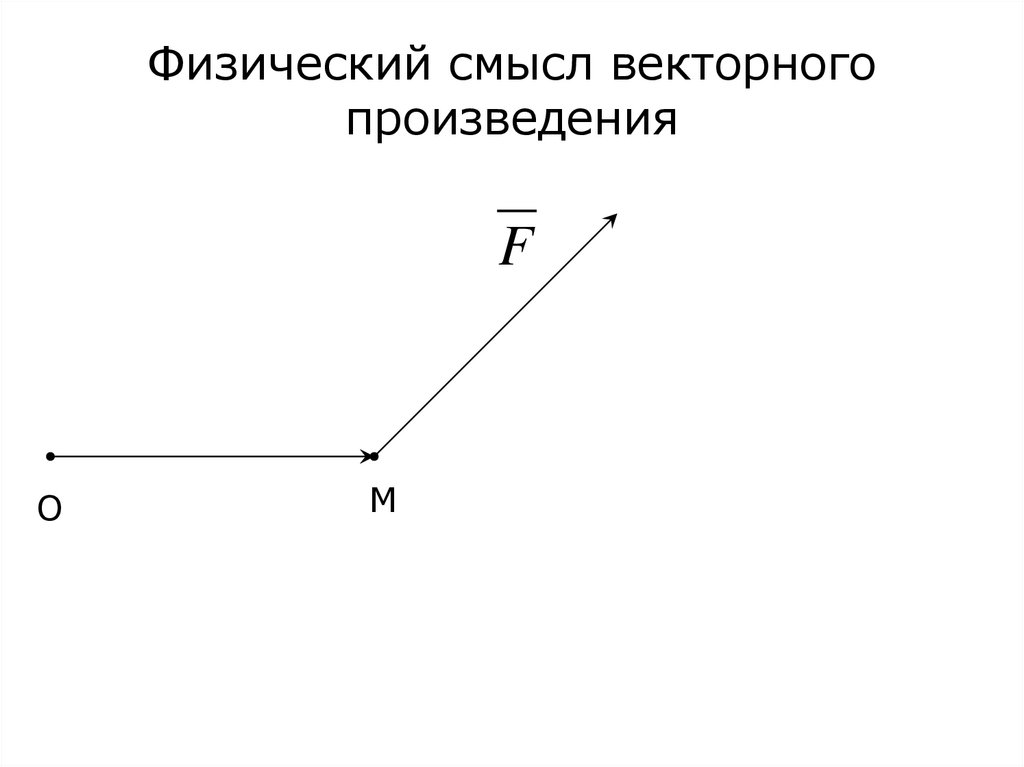
5. Физический смысл векторного произведения
Если F – сила, приложенная к точке М,то момент этой силы относительно точки
О равен векторному произведению
векторов F и OM .
6. Физический смысл векторного произведения
FO
M
7. Пример
Найти векторное произведение векторовa 2i 3 j k ,
b 3i j 4 k .
Решение
i
j
k
3 1
a b 2 3 1
i
1 4
3 1 4
2 1
2 3
j
k 13i 5 j 11k .
3 4
3 1
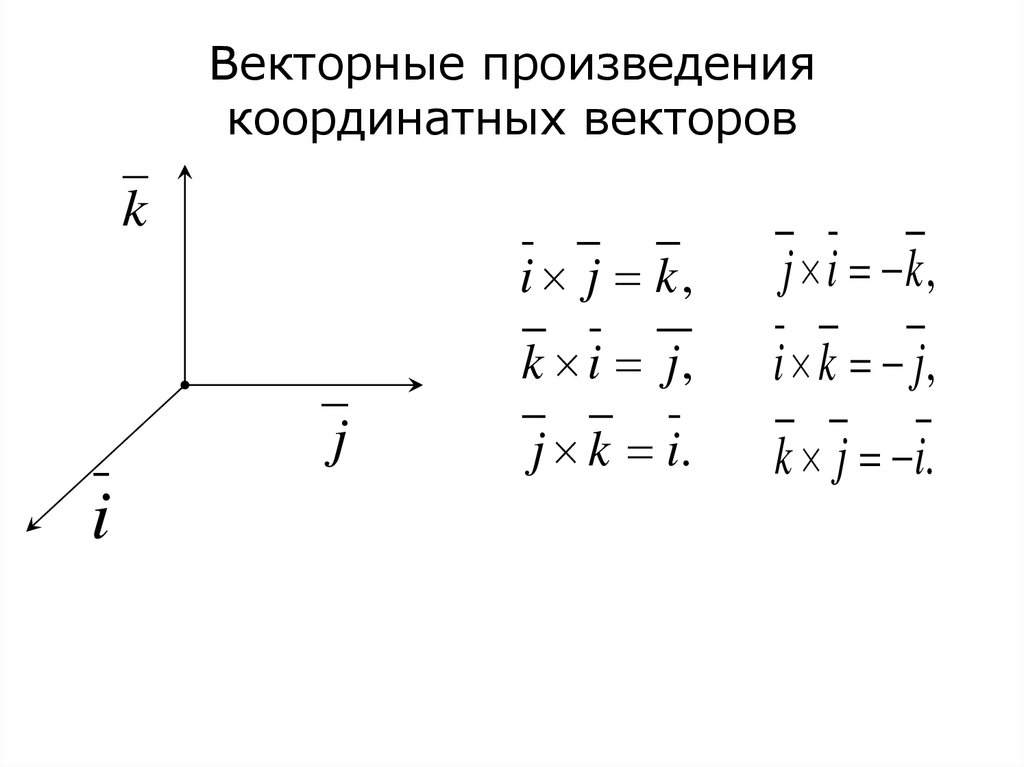
8. Векторные произведения координатных векторов
kj
i
i j k,
j i k ,
k i j,
i k j,
j k i.
k j i.
9. Векторное произведение в координатной форме
ij
k
a b ax ay
bx by
az
bz
10. Площадь параллелограмма
Sпар a b11. Площадь треугольника
1S a b
2
12. Свойства векторного произведения
a b b aa b 0 a 0 или b 0 или a b
a a 0
13. Свойства векторного произведения
( a b) c a c b c(a b) ( a) b a ( b)
14. Пример
Найти2a 3b a 2b ,
0
a
2
,
b
1
,
90
.
если
Решение
2a 3b a 2b
2 a a 3 b a 4 a b 6 b b
7 b a 7 b a sin
7 1 2 sin 90 14 .
0
15. Смешанное произведение
Смешанным произведением трёхвекторов называется произведение
вида :
( a b) c
16. Смешанное произведение
ax ay aza bc b x b y b z
cx c y cz
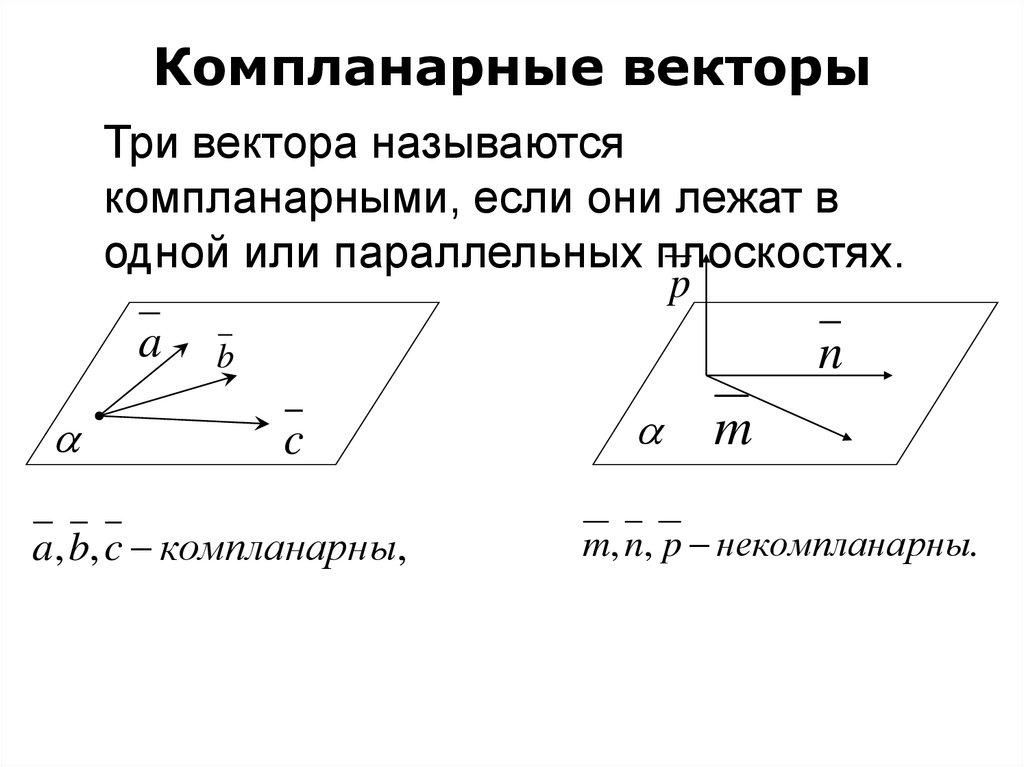
17. Компланарные векторы
Три вектора называютсякомпланарными, если они лежат в
одной или параллельных плоскостях.
p
a b
n
c
a, b, c компланарн ы,
m
m, n, p некомплана рны.
18. Условие компланарности трёх векторов
Еслиa , b, c
компланарны, то
ax
bx
cx
ay
by
cy
az
bz 0.
cz
Элементами определителя являются координаты
векторов
a , b, c
19. Объём параллелепипеда
V abc20. Объём тетраэдра
1Vтет abc
6







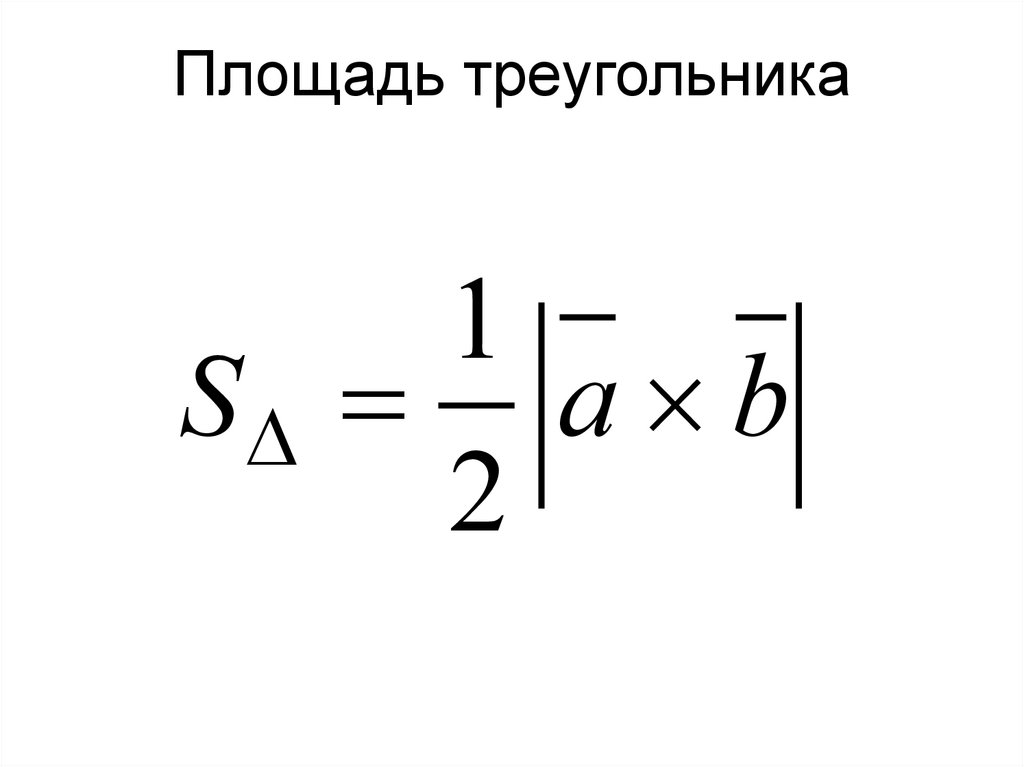






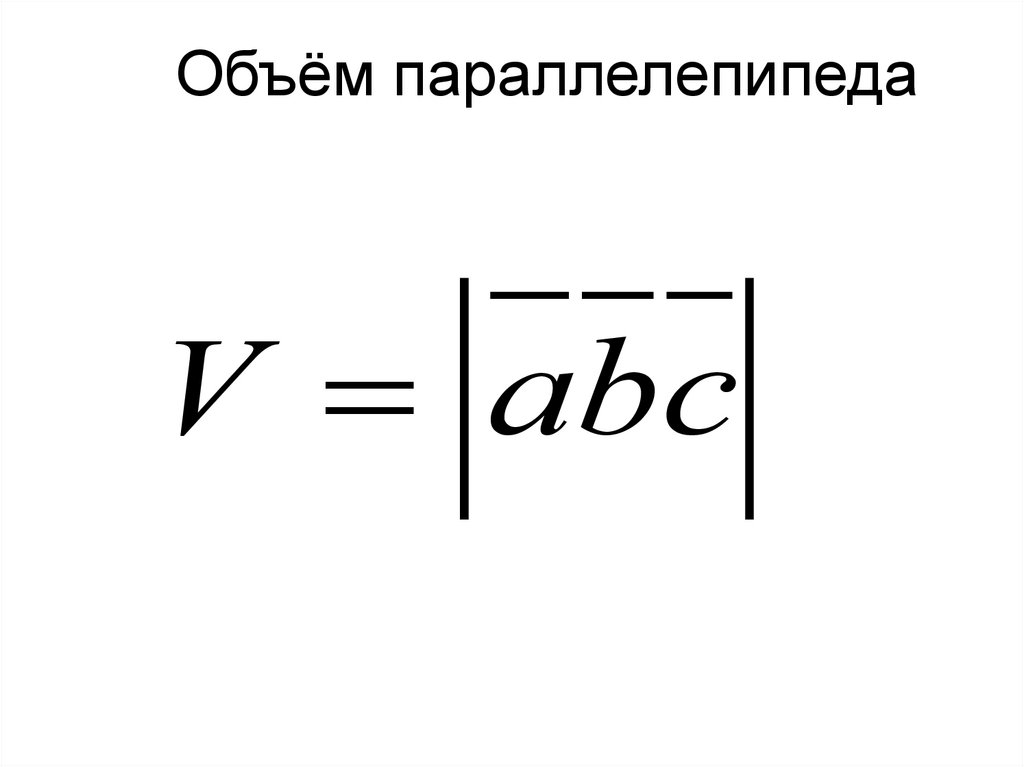
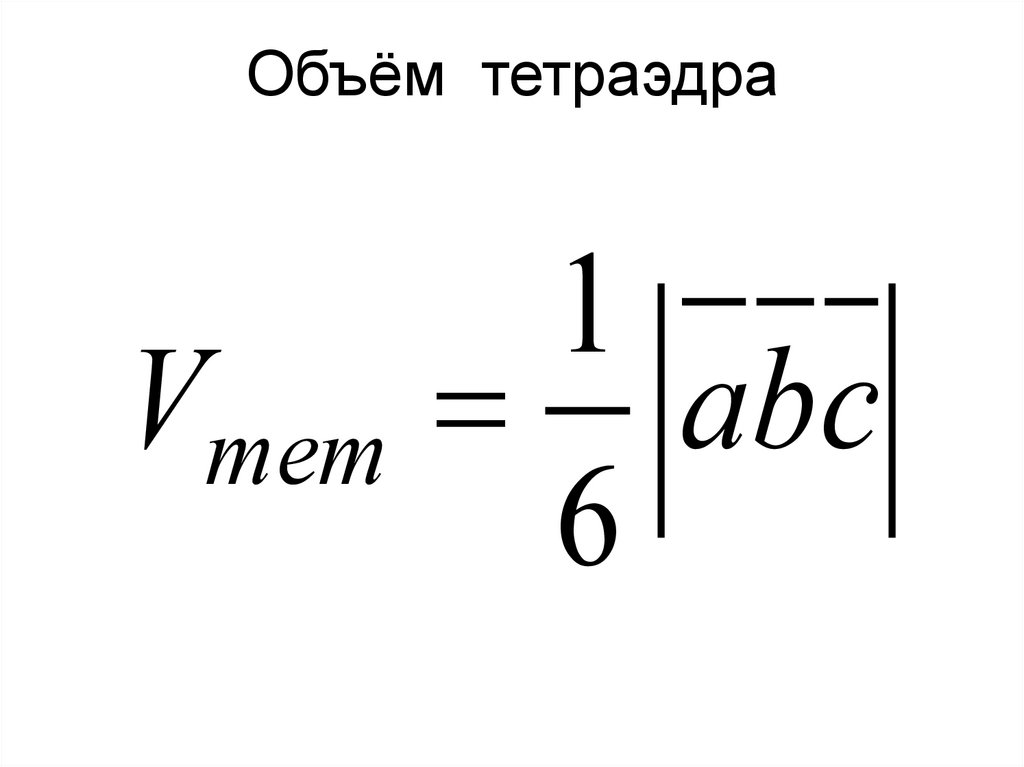
 mathematics
mathematics








