Similar presentations:
Теория Пределов
1.
Теория пределовhttp://www.ltk-college.ru/files/teor_pred.pdf
2.
План1. Последовательности. Предел последовательности.
2. Функции. Предел функции.
3. Геометрический смысл предела. (самостоятельно
4. Бесконечно малые, бесконечно большие.
5. Основные неопределенности. Замечательные
пределы.
3.
Определение: Бесконечной числовойпоследовательностью (или последовательностью)
называют бесконечное множество чисел (членов
последовательности), расположенных в
определенном порядке одно за другим и
построенных по
определенному правилу.
4.
Это правило удобнее задавать ввиде формулы для общего члена
последовательности
, выражающей
функциональную зависимость
от
целочисленного аргумента
, т.е.
Примеры:
1) Общий член
последовательность
определяет
5.
2) Общий членопределяет
последовательность членов геометрической
прогрессии со знаменателем
3) Общий член
последовательность
определяет
6.
Некоторые последовательности обладаюттем свойством, что члены ее по
роста
мере
номера n неограниченно
приближаются
к постоянному числу а.
Так, например, члены последовательностей
1 и 2 неограниченно приближаются к а = 0,
члены последовательности 3 приближаются
к а = 1.
7.
Определение:Число в называется
пределом функции в точке а, если для
всех значений х, достаточно близких к а
и отличных от а, значение функции f(х)
сколь угодно мало отличается от в.
lim
x a
f x b
8.
Функция f(x) называется бесконечно малойпри х → а, если
lim f x 0
x a
Функция f(x) называется бесконечно большой
при х → а, если
lim f x
x a
lim f x
x a
или
9.
Основные теоремы о пределах• Предел суммы (разности) двух функций равен сумме (разности)
их пределов:
lim x x0 ( f ( x) g ( x)) lim x x0 f ( x) lim x x0 g ( x)
• Предел произведения двух функций равен произведению их
пределов:
lim x x0 ( f ( x) g ( x)) lim x x0 f ( x) lim x x0 g ( x)
• Постоянный множитель можно выносить за знак предела:
lim x x0 с f ( x) с lim x x0 f ( x)
• Функция может иметь только один предел при x x
0
10.
Основные теоремы о пределах• Предел степени с натуральным показателем равен той же
степени предела:
lim x x0 ( f ( x))n ( lim x x0 f ( x))n
• Предел дроби равен пределу числителя, делённому на предел
знаменателя, если предел знаменателя не равен нулю:
lim x x0
f ( x) lim x x0 f ( x)
, (lim x x0 g ( x) 0)
g ( x) lim x x0 g ( x)
11.
Замечательные пределы• I ЗП (первый замечательный предел)
sin x
lim x 0
1
x
• I I ЗП
(второй замечательный предел)
1 x
lim x (1 ) e
x
или
1
y
lim y 0 (1 y) e
12.
Функция f (x) называется непрерывной вточке x = a, если предел функции при x→ a
равен значению функции при x = a:
13.
Функция f (x) называется непрерывной в точкеx = a, если она в этой точке определена и
бесконечно малому приращению аргумента
соответствует бесконечно малое значение
функции:
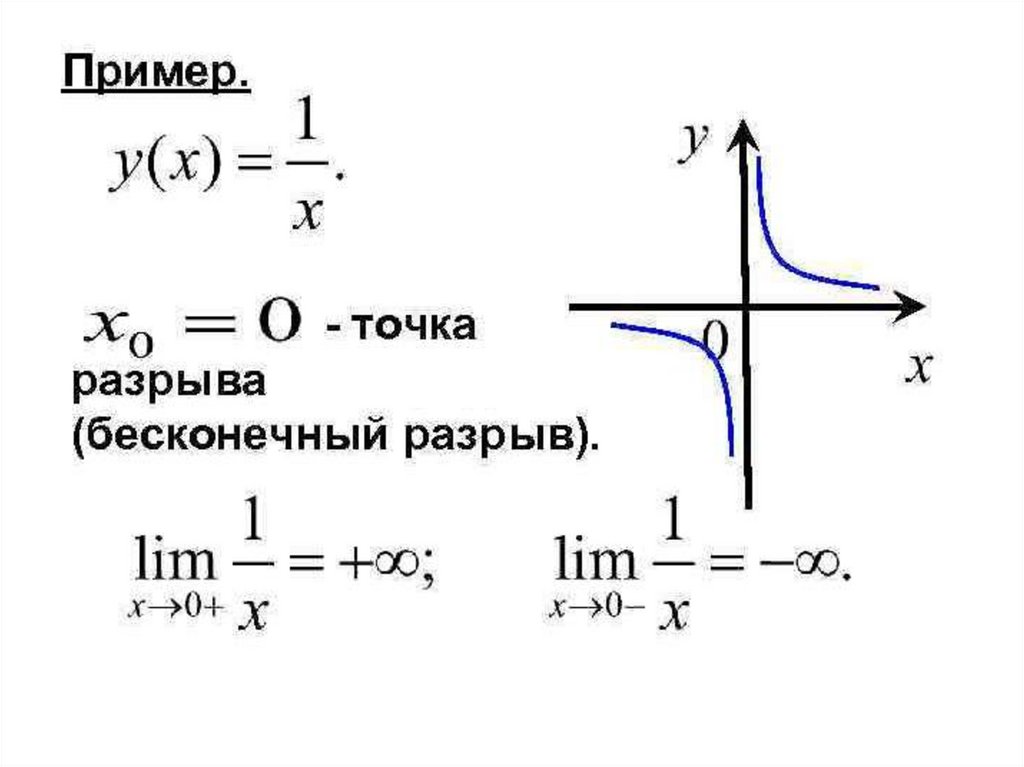
14.
Точки, в которых нарушаетсянепрерывность функции, называются
точками разрыва этой функции.
15.
Для элементарных функций справедливыследующие положения:
область непрерывности элементарной
функции совпадает с её областью
определения, т.е. элементарная функция
непрерывна во всей области определения;
элементарная функция может иметь
разрыв только в отдельных точках
какого-либо промежутка, но не во всех
его точках;
элементарная функция может иметь
разрыв только в той точке, в которой
она не определена.
16.
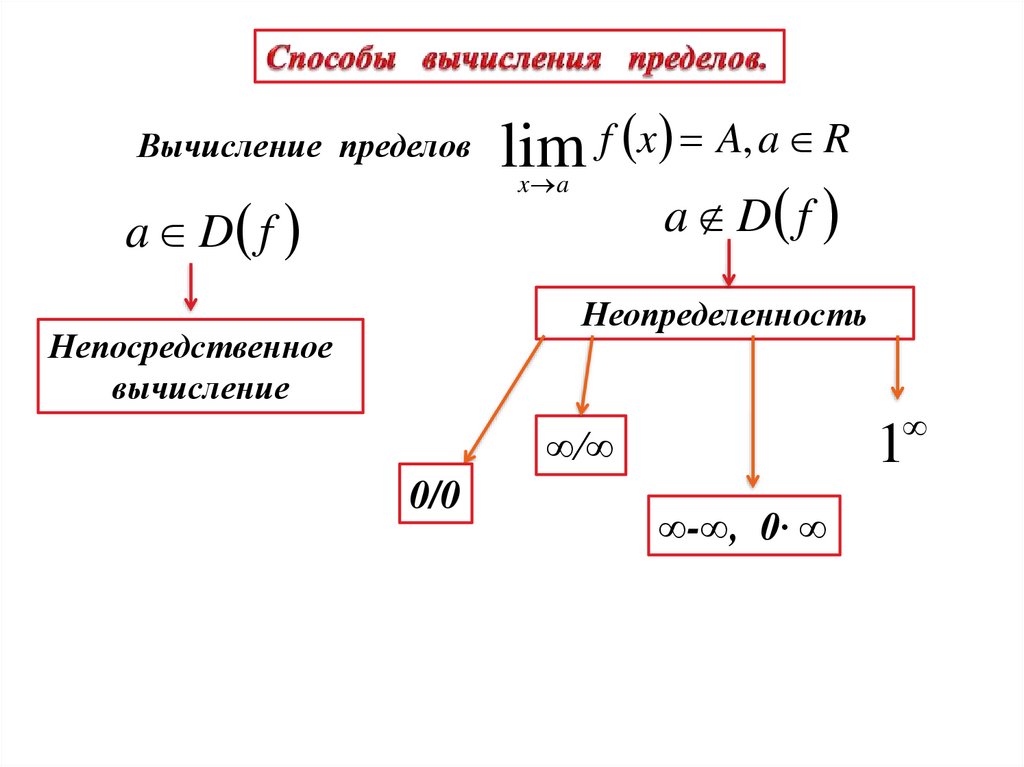
17.
Вычисление пределовlim f x A, a R
a D f
x a
a D f
Неопределенность
Непосредственное
вычисление
1
∞/∞
0/0
∞-∞, 0∙ ∞
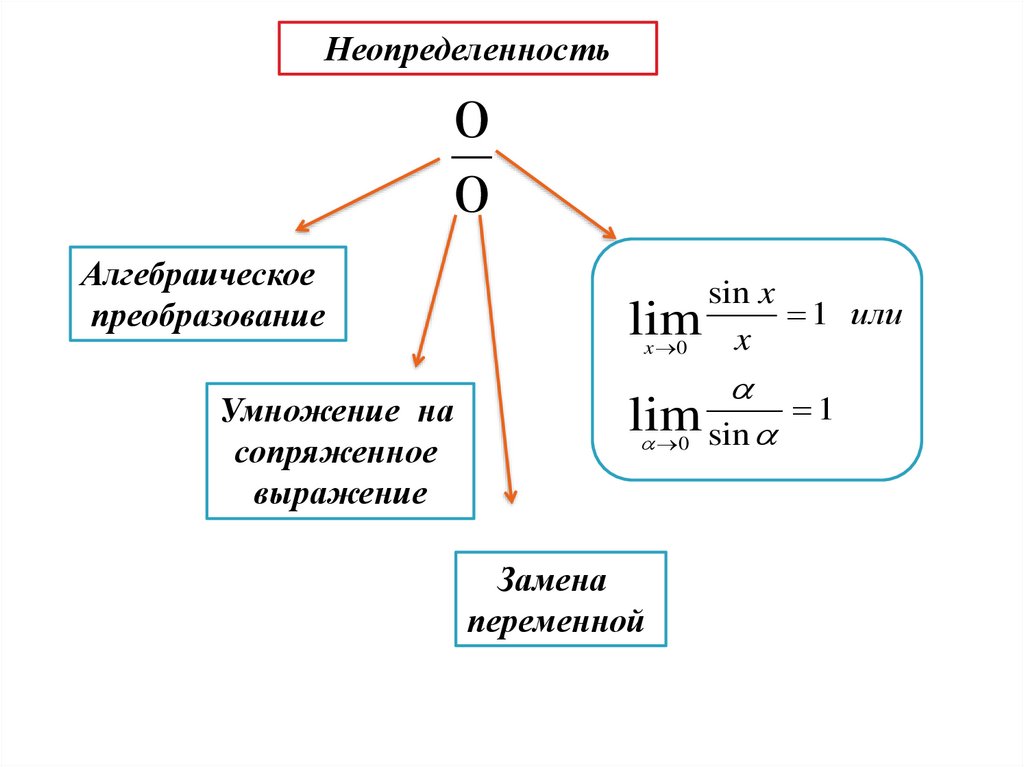
18.
Неопределенность0
0
Алгебраическое
преобразование
Умножение на
сопряженное
выражение
sin x
1 или
lim
x
x 0
lim
sin
0
Замена
переменной
1
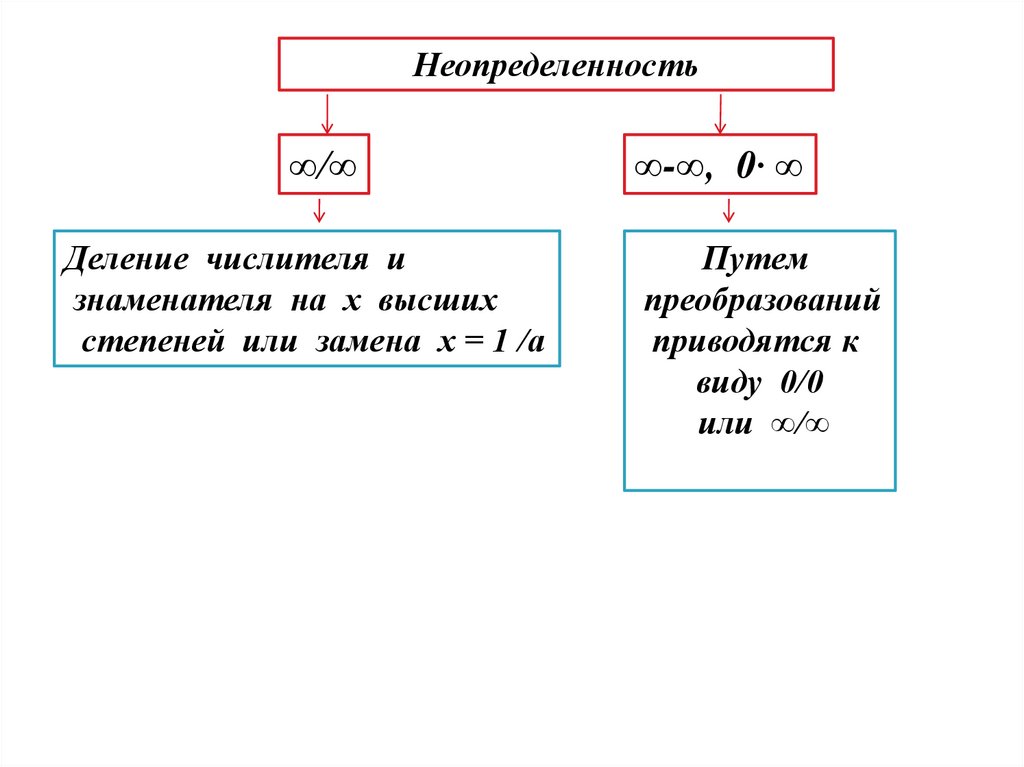
19.
Неопределенность∞/∞
Деление числителя и
знаменателя на х высших
степеней или замена х = 1 /а
∞-∞, 0∙ ∞
Путем
преобразований
приводятся к
виду 0/0
или ∞/∞
20.
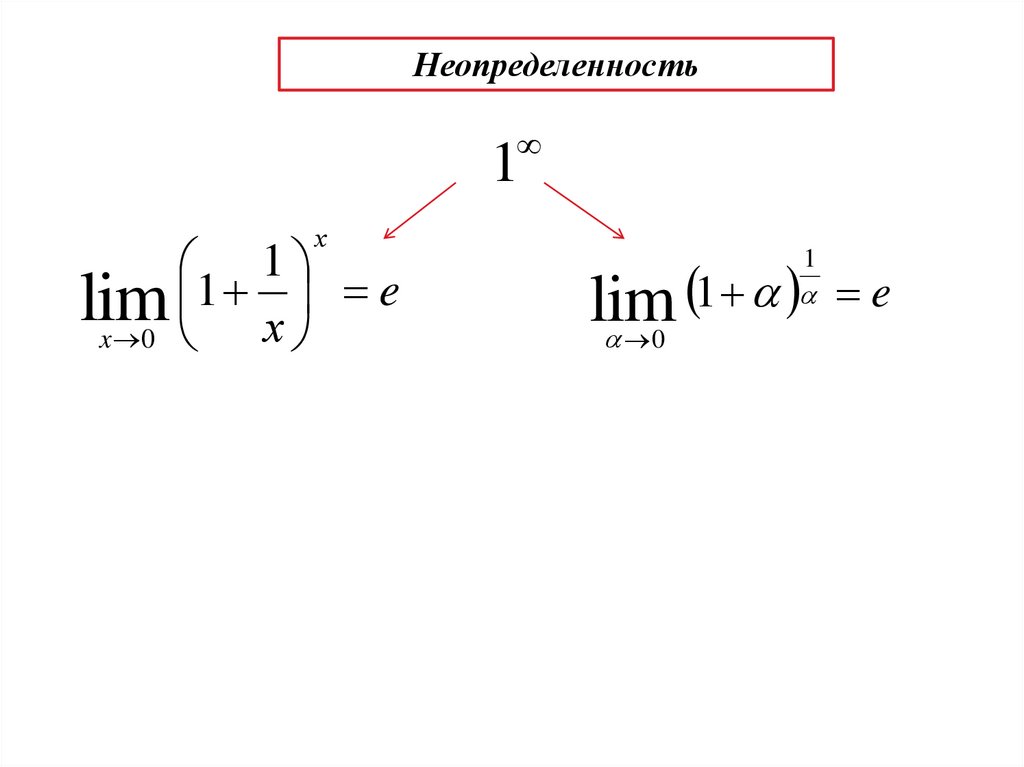
Неопределенность1
х
1
1 e
lim
х
x 0
1
lim
1
0
e
21.
Запомнить!Необходимо помнить, что
C
0
C
0, , C ,
0, , 0 C C.
C
C
0
Более сложными случаями
нахождения
предела
являются
С=const (любое
постоянное
число)
точке x = a или при x→∞ представляет собой неопределенн
1 , 0 0 , 0 ).
При вычислении пределов при x основные теоремы
кроме того, используются правила:
22.
2x2 11) lim 2
;
x 3 x 4 x
Решение:
2x2 1
lim
2
x 3 x 4 x
2x2 1
2
2
2 0 2
x
x
lim 2
.
4x 3 0 3
x 3 x
2
2
x
x
Ответ: 2/3.
23.
5x3 7 x2) lim
;
3
x 1 2 x
Решение:
5x 7 х
lim
3
x 1 2 x
3
5x3 7 х
3
3
5 0
5
x
x
lim
2,5
3
2x
0 2
2
x 1
3
3
x
x
Ответ: - 2,5.
24.
4) limx
2x2 1
;
2x 1
Решение:
lim
x
lim
x
2x2 1
lim
2x 1
x
2x2 1
2x2 1
lim
2
2
2 x 1 x 4 x 4 x 1
2x2 1
2
2
2 0
1
1
x
x
2
4x
4x 1
4 0 0
2
2
x2 x2 x2
25.
5) limx 0
1 x 1
;
x
Решение:
lim
x 0
1 x 1 0
1 x 1 1 x 1
lim
x
0 x 0
x
1 x 1
1 x 1
1 x 1
lim
lim
lim
x 1 x 1
x 1 x 1
2
x 0
2
x 0
x 0
1
1
1 x 1 2
26.
36) lim
x 1
x 1
;
x 1
Решение:
3
lim
x 1
x 1 0
x 1 0
x t6, x t3
3
t 2 1
lim 3
x 1 t 1
x t 2 , x 1, t 1
t 1 t 1
t 1
2
lim
lim 2
2
3
t 1 t 1 t t 1
t 1 t t 1
27.
1 cos 2 x7) lim
;
2
x
x 0
Решение:
1 cos 2 x 0
2 sin x
sin x
lim
2 lim
lim
2
2
x
0 x 0
x
x
x 0
x 0
2 1 2
2
2
28.
1x 2
8) lim
;
x
x
x
Решение:
x 2
2
1 lim 1
lim
x
x
x
x
x
x
2
2
e
2























 mathematics
mathematics








