Сфера. Уравнение сферы

1.

2.

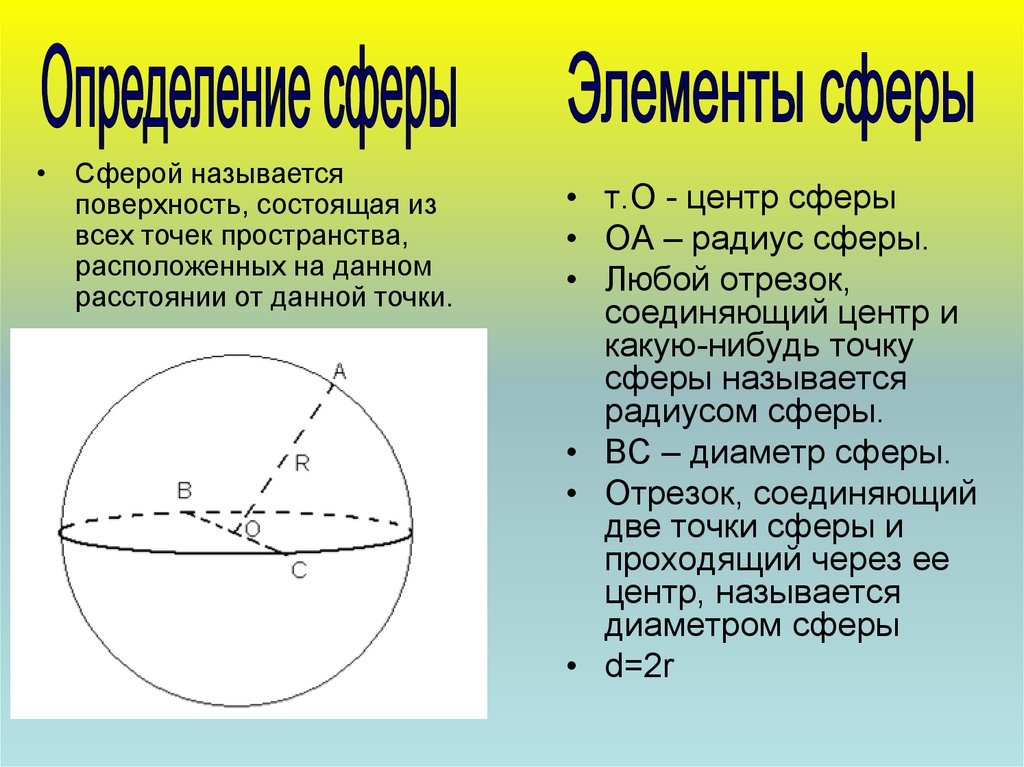
• Сферой называется
поверхность, состоящая из
всех точек пространства,
расположенных на данном
расстоянии от данной точки.
• т.О - центр сферы
• ОА – радиус сферы.
• Любой отрезок,
соединяющий центр и
какую-нибудь точку
сферы называется
радиусом сферы.
• ВС – диаметр сферы.
• Отрезок, соединяющий
две точки сферы и
проходящий через ее
центр, называется
диаметром сферы
• d=2r

3.

у
z
(х;у;z)
М(х;у)
С
х
х х0 у - у0
2
2
х - х 0 у - у0 r 2
d
2
у
2
х
2
2
2
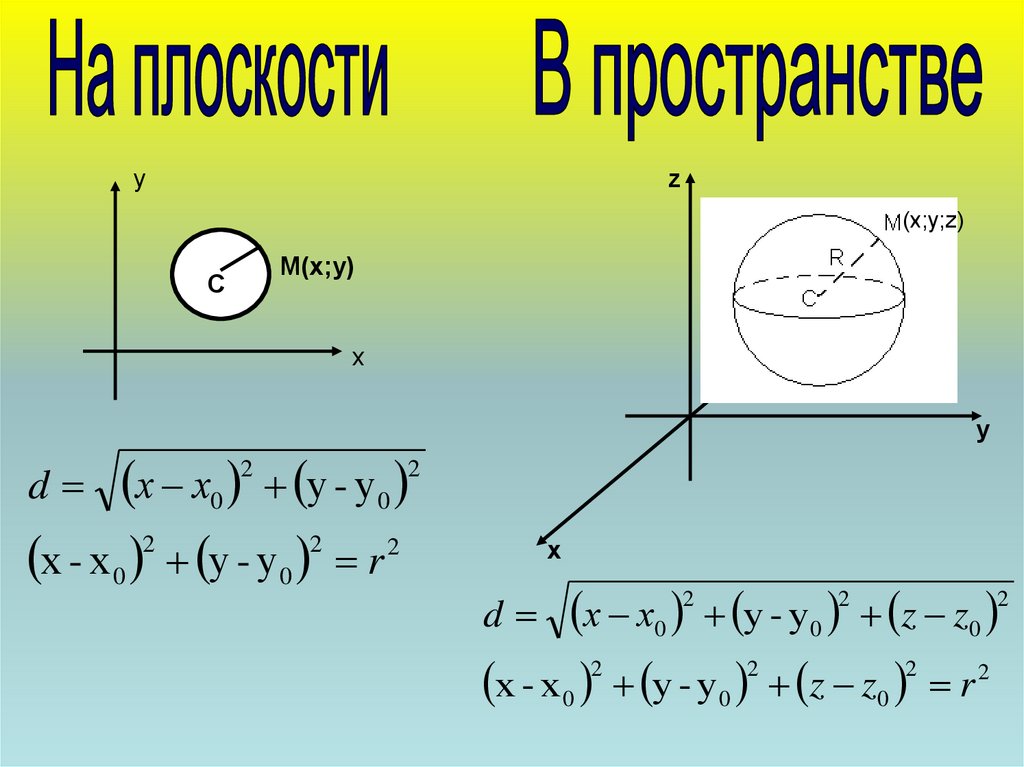
d х х0 у - у 0 z z0
2
2
2
х - х 0 у - у0 z z0 r 2

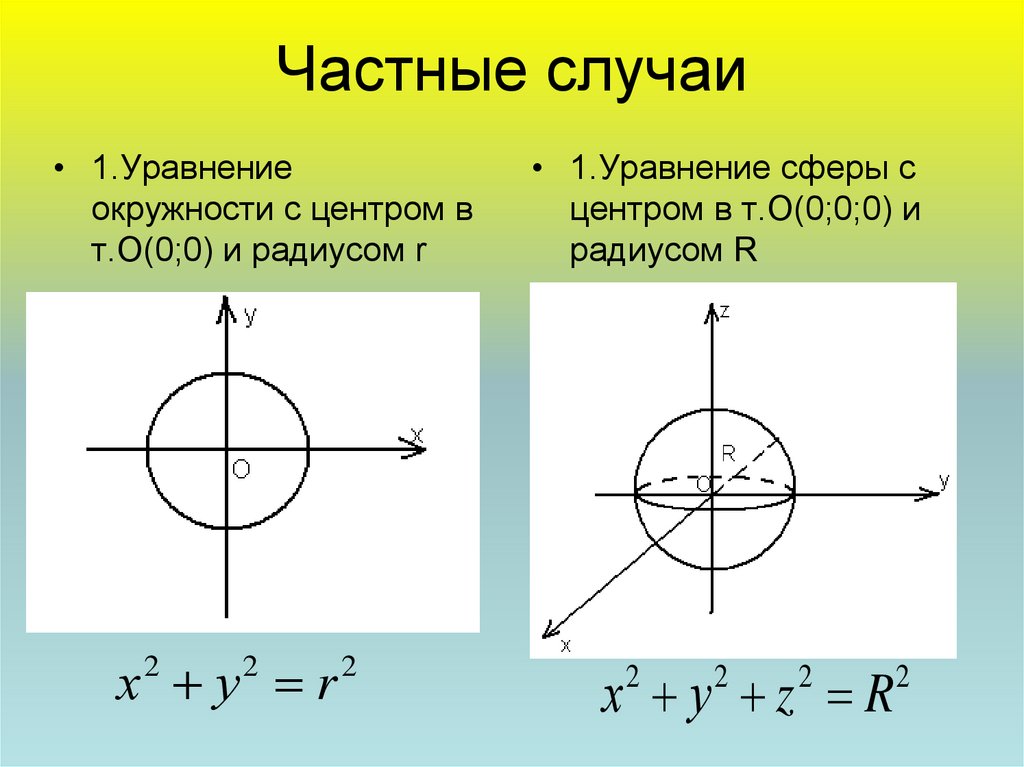
4. Частные случаи

• 1.Уравнение
окружности с центром в
т.О(0;0) и радиусом r
х у r
2
2
2
• 1.Уравнение сферы с
центром в т.О(0;0;0) и
радиусом R
х у z R
2
2
2
2

5.

6. Общее уравнение плоскости

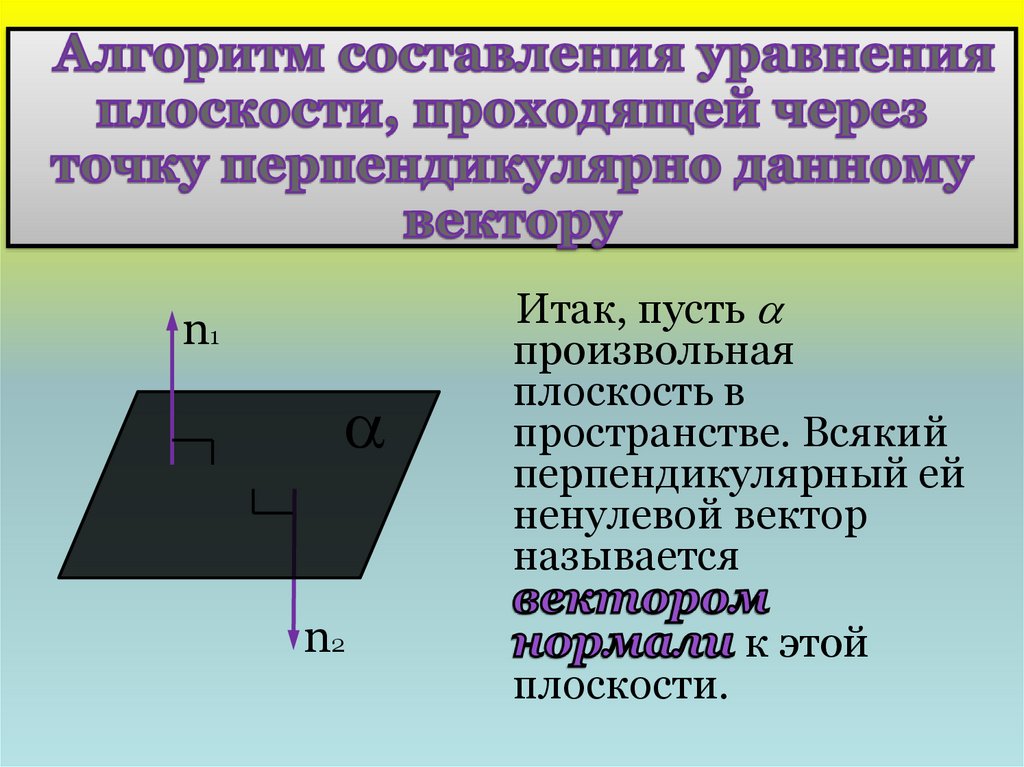
7. Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

n1
n2
Итак, пусть
произвольная
плоскость в
пространстве. Всякий
перпендикулярный ей
ненулевой вектор
называется
плоскости.
к этой

8. Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

n (A;B;C)
M0
Если известна какая-нибудь точка
плоскости M0 и какой-нибудь
вектор нормали к ней, то через
заданную точку можно провести
единственную плоскость,
перпендикулярную данному
вектору. Общее уравнение
плоскости будет иметь вид:

9. Канонические уравнения прямой

Если известна некоторая точка пространства M(x0; y0; z0),
принадлежащая прямой, и направляющий вектор p(p1; p2;
p3) данной прямой, то канонические уравнения этой прямой
выражаются формулами:
Приведённая запись предполагает, что координаты
направляющего вектора не равны нулю.