Similar presentations:
Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы
1. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы.
СфераСФЕРА И ШАР. УРАВНЕНИЕ
СФЕРЫ. ВЗАИМНОЕ
РАСПОЛОЖЕНИЕ СФЕРЫ И
ПЛОСКОСТИ. ПЛОЩАДЬ
СФЕРЫ.
2. Сфера и шар
Сферой называется поверхность,состоящая из всех точек пространства,
расположенных на данном расстоянии от
данной точки.
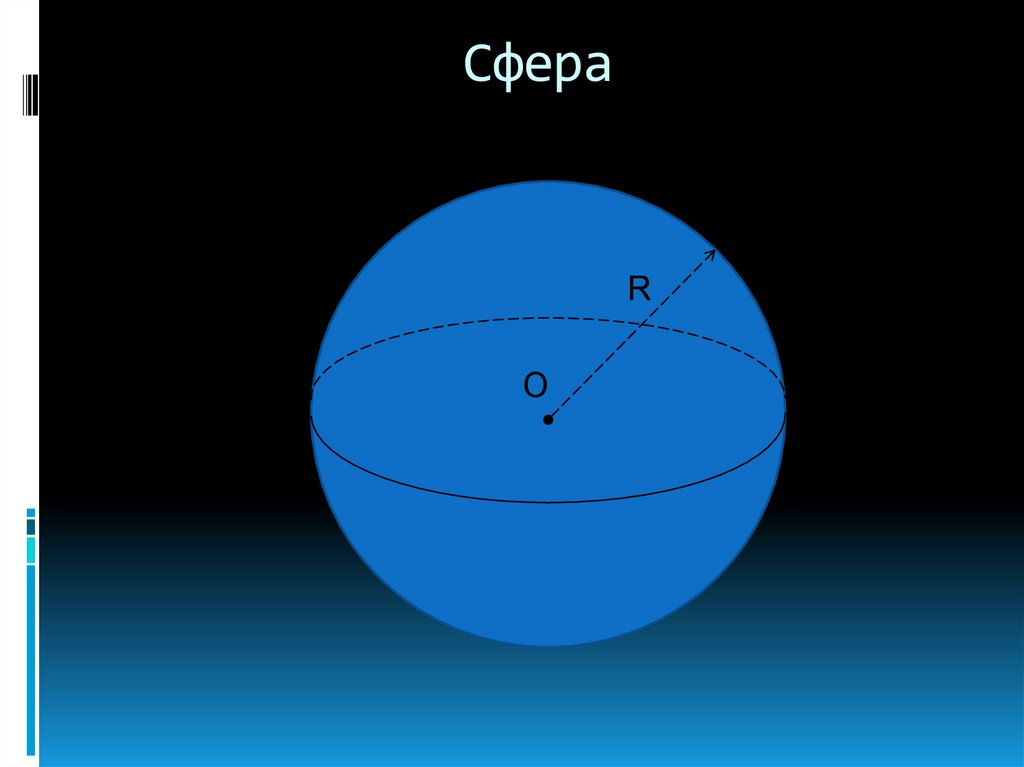
Данная точка называется центром сферы
(точка О на рисунке), а данное расстояние
— радиусом сферы. Радиус сферы часто
обозначают латинской буквой R.
3. Сфера
RО
4.
Любой отрезок, соединяющий центри какую-нибудь точку сферы, также
называется радиусом сферы.
Отрезок, соединяющий две точки
сферы и проходящий через ее центр,
называется диаметром сферы.
Очевидно, диаметр сферы равен 2R.
Отметим, что сфера может быть
получена вращением полуокружности
вокруг ее диаметра.
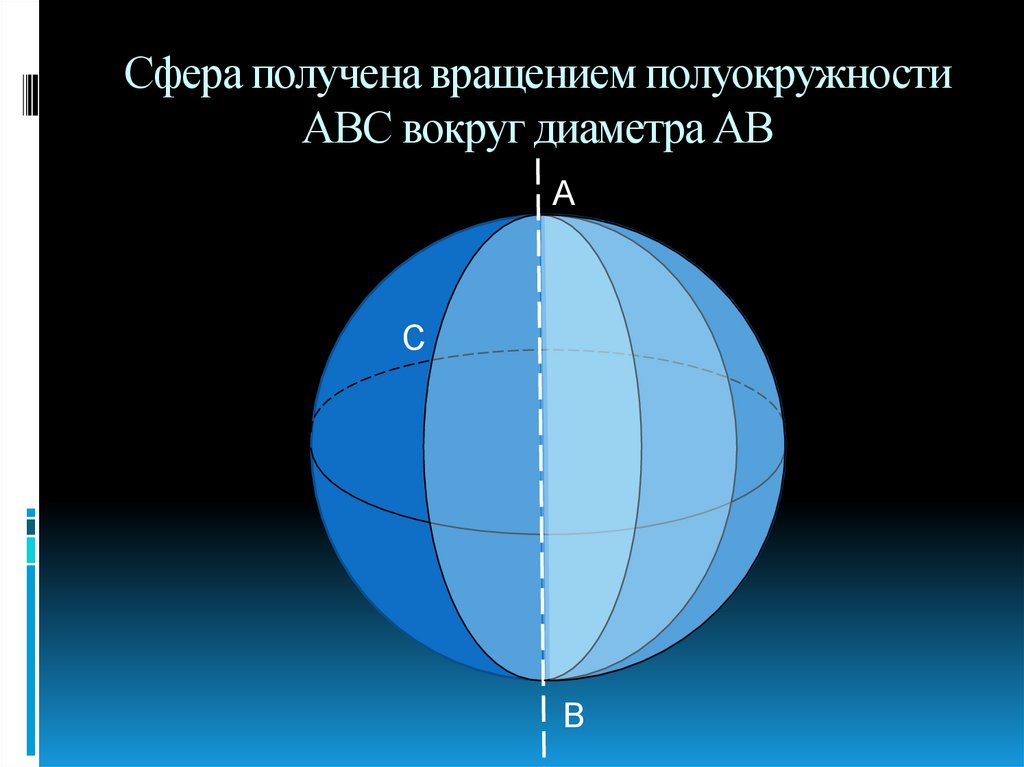
5. Сфера получена вращением полуокружности АВС вокруг диаметра АВ
АС
В
6.
Тело, ограниченное сферой,называется шаром. Центр, радиус и
диаметр сферы называются также
центром, радиусом и диаметром шара.
Очевидно, шар радиуса R с центром О
содержит все точки пространства,
которые расположены от точки О на
расстоянии, не превышающем R
(включая и точку О), и не содержит
других точек.
7. Уравнение сферы
Пусть заданы прямоугольная системакоординат Oxyz и дана некоторая
поверхность F, например плоскость или
сфера. Уравнение с тремя переменными
x,y,z называется уравнением
поверхности F, если этому уравнению
удовлетворяют координаты любой точки
поверхности F и не удовлетворяют
координаты никакой точки, не лежащей
на этой поверхности.
8.
Отметим, что понятие уравненияповерхности аналогично понятию
уравнения линии, которое было введено
в курсе планиметрии.
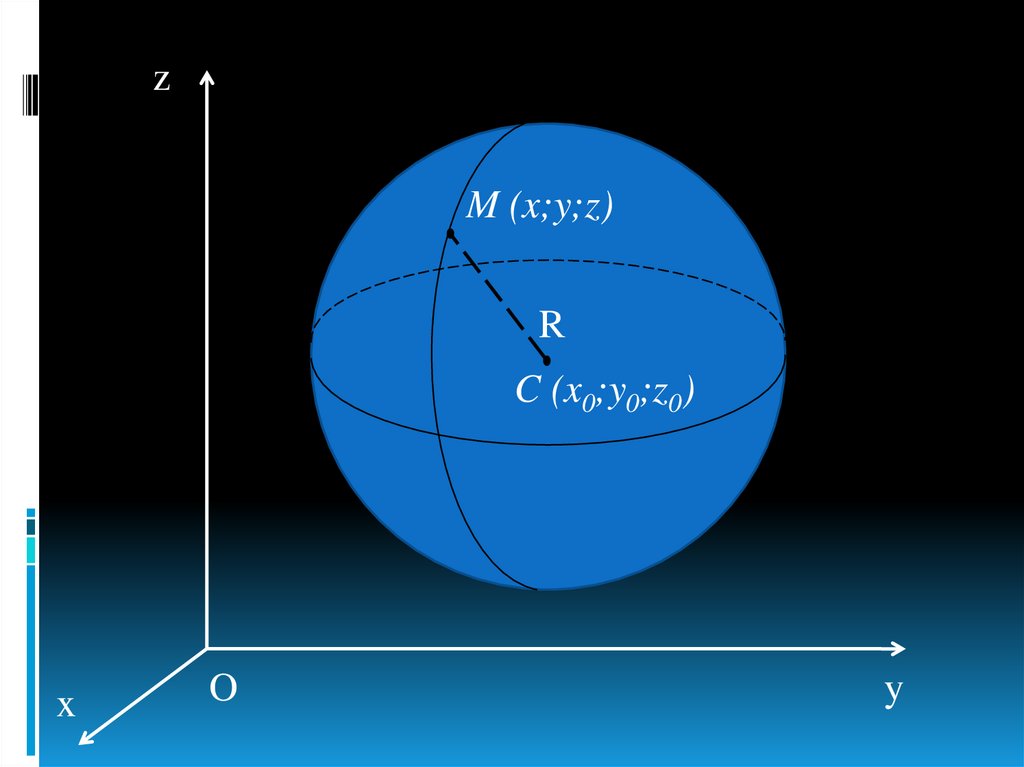
Введем уравнение сферы радиуса R с
центром C (x0;y0;z0).
9.
zM (x;y;z)
R
C (x0;y0;z0)
x
O
y
10.
Расстояние от произвольной точки M(x;y;z) до точки С вычисляется по формуле:
MC=
2
2
(х-х0) +(у-у0)
+(z-z0
2
)
11.
Если точка М лежит на данной сфере, тоМС = R, или МС2 = R2, т. е. координаты точки
М удовлетворяют уравнению
(х-х0)2+(у-у0)2 +(z-z0)2 = R2
(1)
12.
Если же точка М (х; у; z) не лежит на данной сфере, то МС2 =R2, т. е. координатыточки М не удовлетворяют уравнению (1).
Следовательно, в прямоугольной системе
координат уравнение сферы радиуса R с
центром С (х0; у0; z0) имеет вид
(х-х0)2 + (у-у0)2 + (z-z0)2 =R2.
13. Взаимное расположение сферы и плоскости
Исследуем взаимное расположениесферы и плоскости в зависимости от
соотношения между радиусом сферы и
расстоянием от ее центра до плоскости.
Обозначим радиус сферы буквой R, а
расстояние от ее центра до плоскости α
— буквой d.
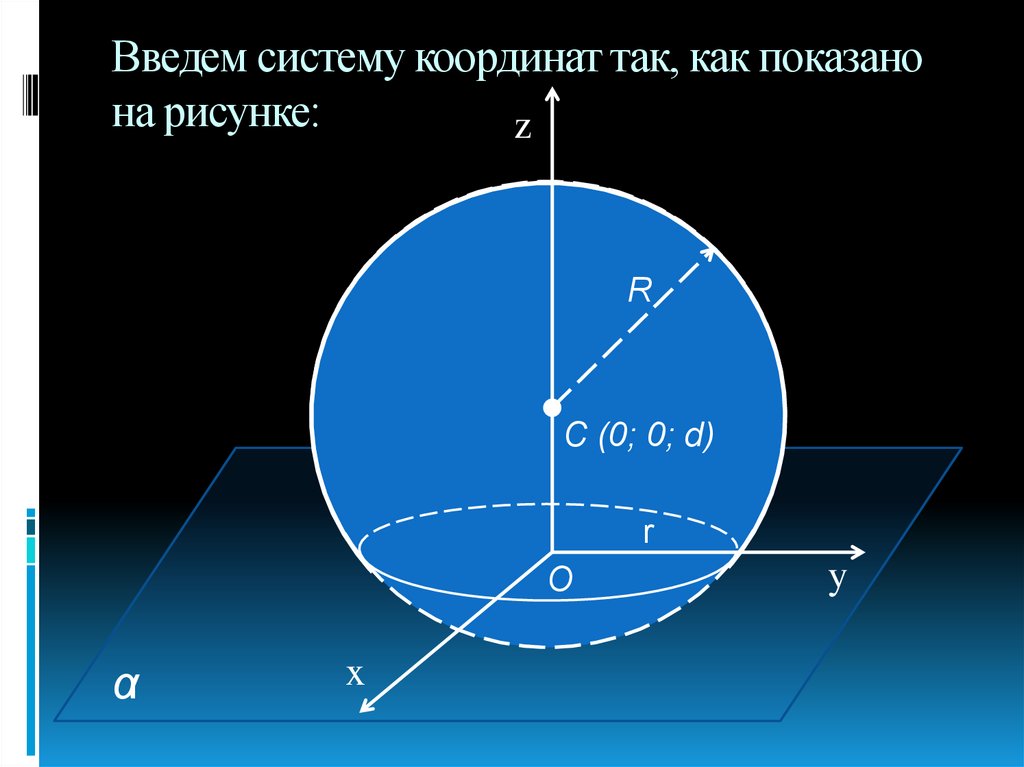
14. Введем систему координат так, как показано на рисунке:
zR
С (0; 0; d)
r
О
α
x
y
15.
Плоскость Оху совпадает с плоскостью α,а центр С сферы лежит на положительной
полуоси Oz. В этой системе координат точка
С имеет координаты (0; 0; d), поэтому сфера
имеет уравнение
2
2
2
2
х + у + (z – d) = R
Плоскость α совпадает с координатной
плоскостью Оху, и поэтому ее уравнение
имеет вид z = 0.
16. Если координаты какой-нибудь точки М (х; у; z) удовлетворяют обоим уравнениям, то точка М лежит как в плоскости α, так и на
Если координаты какой-нибудь точки М(х; у; Z) удовлетворяют обоим уравнениям, то
точка М лежит как в плоскости α, так и на
сфере, т. е. является общей точкой плоскости и
сферы. Если же система этих двух уравнений
не имеет решений, то сфера и плоскость не
имеют общих точек.
17. Таким образом, вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений z = 0 х2 +у2 +(z -
Таким образом, вопрос о взаимномрасположении сферы и плоскости сводится к
исследованию системы уравнений
Z=0
х2 +у2 +(Z - d)2 = R2
Подставив Z = 0 во второе уравнение,
получим
х2 +у2 =R2 - d2
(2)
Возможны три случая.
18. 1) d < R. Тогда R2 - d2 > 0, и уравнение (2) является уравнением окружности радиуса r = R2 -d2 с центром в точке О на плоскости
1) d < R. Тогда R2 - d2 > 0, и уравнение (2)является уравнением окружности радиуса
r = R2 -d2 с центром в точке О на плоскости
Оху. Координаты любой точки М (х; у; 0) этой
окружности удовлетворяют как уравнению
плоскости а, так и уравнению сферы, т. е. все
точки этой окружности являются общими точками плоскости и сферы. Таким образом, в
данном случае сфера и плоскость
пересекаются по окружности.
19.
d<R, r = R2 -d2R
С (0; 0; d)
r
О
20. Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность. Ясно,
Итак, если расстояние от центра сферыдо плоскости меньше радиуса сферы, то
сечение сферы плоскостью есть окружность.
Ясно, что сечение шара плоскостью есть
круг. Если секущая плоскость проходит через
центр шара, то d = 0 и в сечении получается
круг радиуса R, т. е. круг, радиус которого
равен радиусу шара. Такой круг называется
большим кругом шара. Если секущая
плоскость не проходит через центр шара, то
d > 0 и радиус сечения r = R2 -d2, очевидно,
меньше радиуса шара.
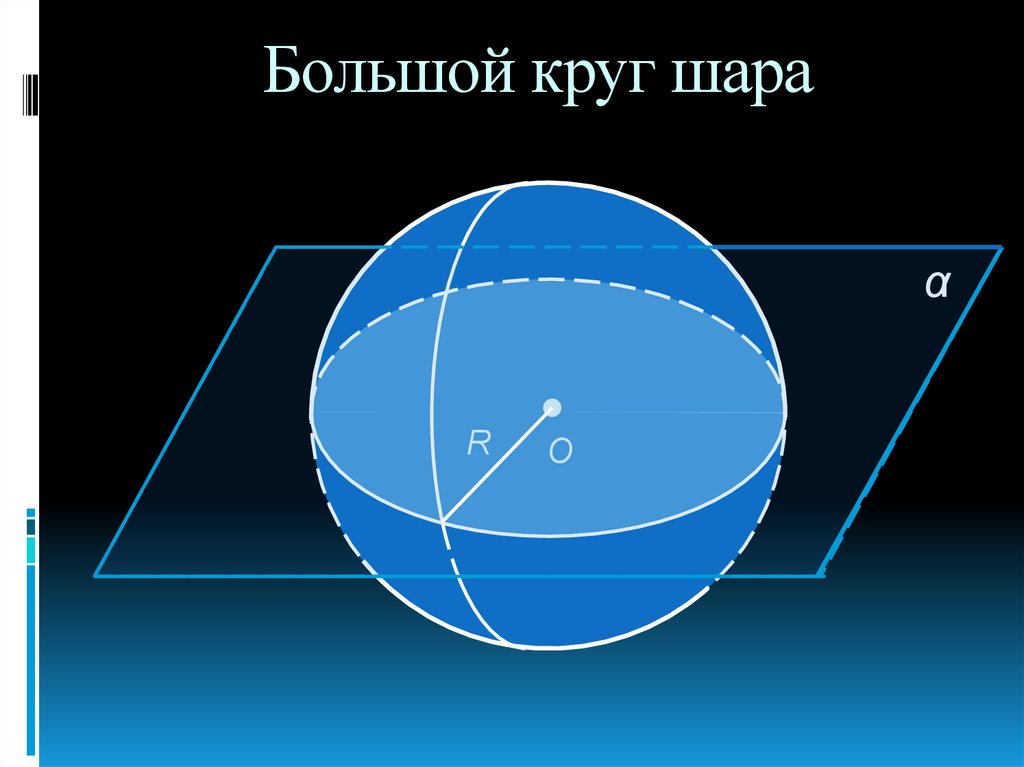
21. Большой круг шара
αR
О
22. 2) d = R. Тогда R2 - d2 = 0, и уравнению (2) удовлетворяют только числа х = 0, у = 0. Следовательно, только координаты точки О
(0; 0; 0) удовлетворяют обоим уравнениям,т. е. О — единственная общая
точка сферы и плоскости.
Итак, если расстояние от центра
сферы до плоскости равно радиусу сферы,
то сфера и плоскость имеют только одну
общую точку.
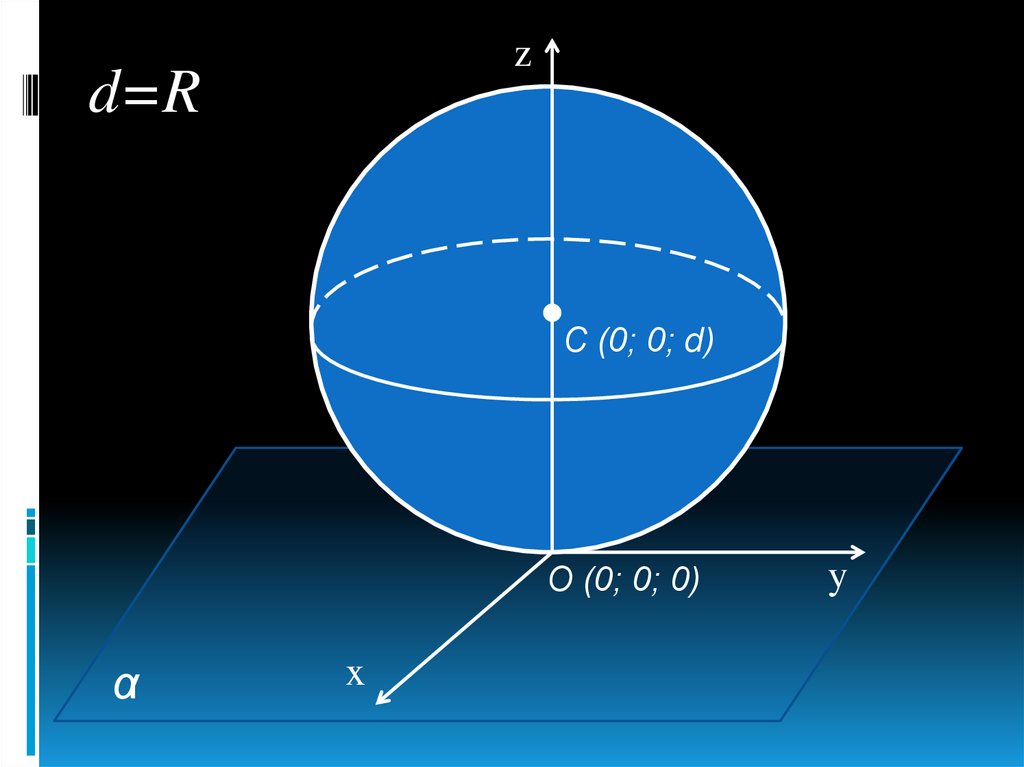
23.
zd=R
С (0; 0; d)
О (0; 0; 0)
α
x
y
24. 3) d> R. Тогда R2 - d2 < 0, и уравнению (2) не удовлетворяют координаты никакой точки. Следовательно, если расстояние от центра
3) d> R. Тогда R2 - d2 < 0, и уравнению (2) неудовлетворяют координаты никакой точки.
Следовательно, если расстояние от центра
сферы до плоскости больше радиуса сферы,
то сфера и плоскость не имеют общих точек.
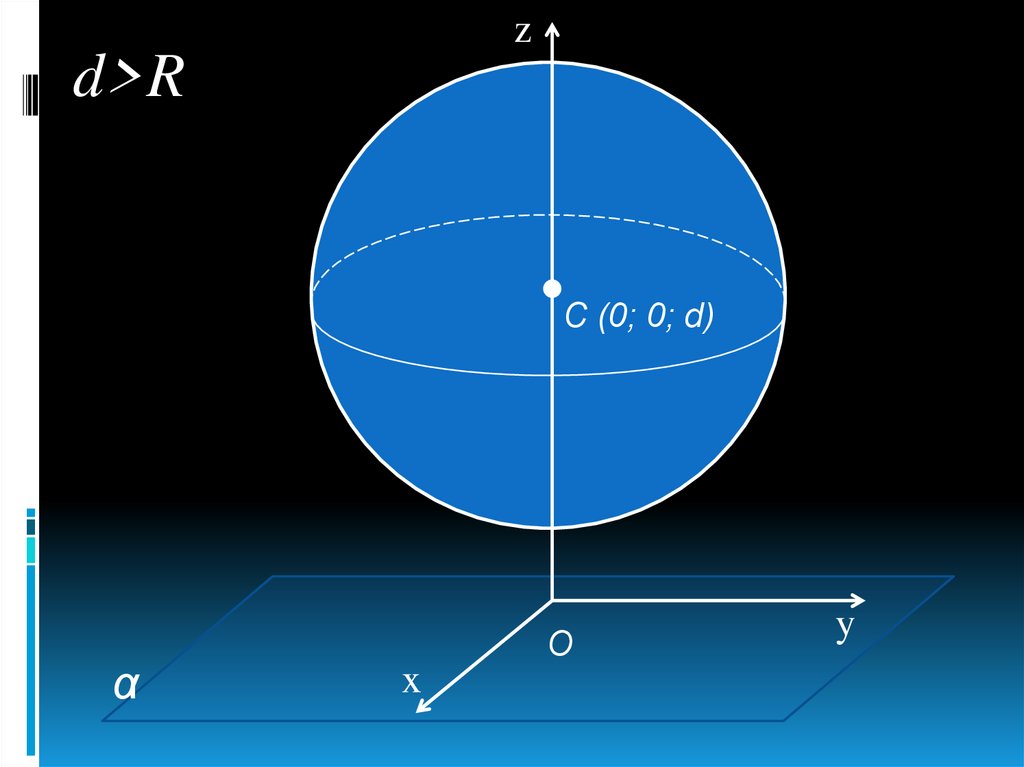
25.
zd>R
С (0; 0; d)
α
О
x
y
26. Касательная плоскость к сфере
Рассмотрим более подробно случай,когда сфера и плоскость имеют только
одну общую точку. Плоскость, имеющая
со сферой только одну общую точку,
называется касательной плоскостью к
сфере, а их общая точка называется
точкой касания плоскости и сферы.
27. Теорема: Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
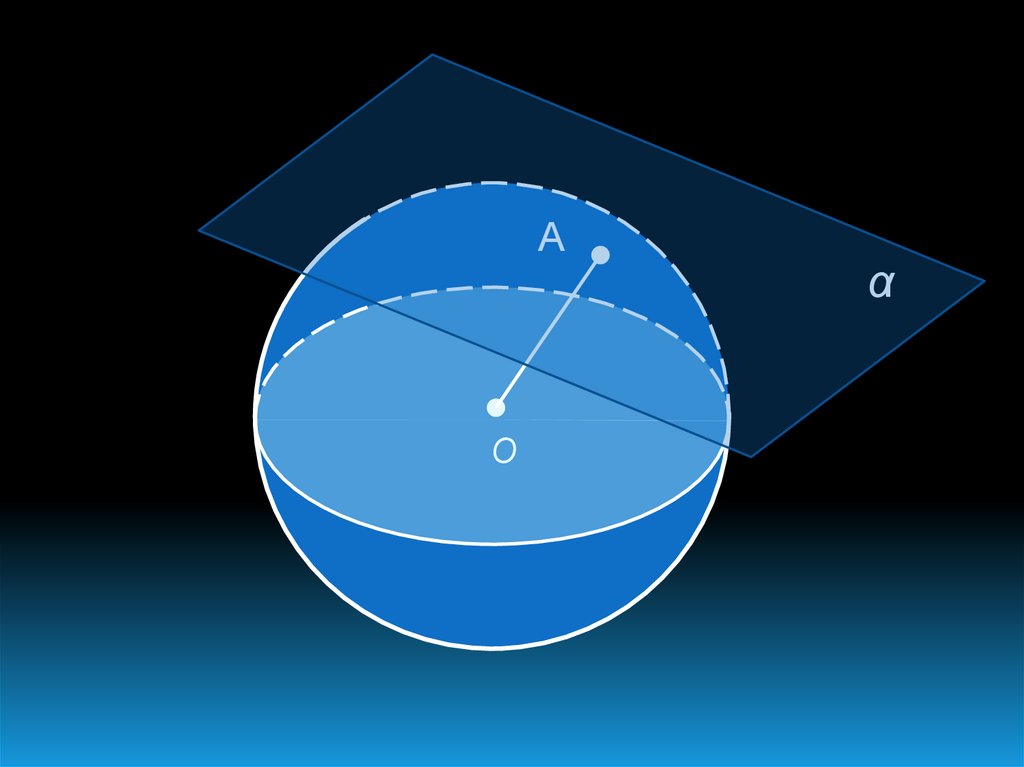
28.
АО
α
29. Доказательство: Рассмотрим плоскость α, касающуюся сферы с центром О в точке А. Докажем, что радиус OA перпендикулярен к
плоскости α.Предположим, что это не так. Тогда радиус OA
является наклонной к плоскости α, и,
следовательно, расстояние от центра сферы до
плоскости α меньше радиуса сферы. Поэтому
сфера и плоскость пересекаются по
окружности.
30. Но это противоречит тому, что плоскость α — касательная, т. е. сфера и плоскость α имеют только одну общую точку. Полученное
противоречие доказывает, что радиус OAперпендикулярен к плоскости α.
Теорема доказана.
Докажем обратную теорему.
31. Теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является
касательнойк сфере.
32. Доказательство : Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из центра сферы к данной
плоскости. Поэтому расстояние от центрасферы до плоскости равно радиусу сферы, и,
следовательно, сфера и плоскость имеют
только одну общую точку. Это и означает, что
данная плоскость является касательной к
сфере. Теорема доказана.
33. Площадь сферы
В отличие от боковой поверхностицилиндра или конуса сферу нельзя
развернуть на плоскость, и,
следовательно, для нее непригоден способ
определения и вычисления площади
поверхности с помощью развертки. Для
определения площади сферы
воспользуемся понятием описанного
многогранника.
34. При этом сфера называется вписанной в многогранник. На рисунке изображены описанные около сферы тетраэдр и куб. Рассмотрим
последовательностьописанных около данной сферы
многогранников, в которой число граней
многогранника неограниченно возрастает и
при этом наибольший размер каждой грани**
многогранника стремится к нулю. За площадь
сферы примем предел последовательности
площадей поверхностей этих многогранников.
35. Формула для вычисления площади сферы радиуса R:
S=2
4πR



























 mathematics
mathematics








