Тела вращения. Сфера и шар

1. Тела вращения

Сфера
Шар

2. История возникновения

Из истории возникновения. Шаром принято называть
тело, ограниченное сферой, т.е. шар и сфера – это
разные геометрические тела. Однако оба слова « шар»
и « сфера» происходят от одного и того же греческого
слова « сфайра» - мяч. При этом слово « шар»
образовалось от перехода согласных сф в ш. В XI книге
«Начал» Евклид определяет шар как фигуру,
описанную вращающимся около неподвижного
диаметра полукругом. В древности сфера была в
большом почёте. Астрономические наблюдения над
небесным сводом неизменно вызывали образ сферы.
Сфера всегда широко применялось в различных
областях науки и техники.

3. Сфера и шар в жизни людей

4.

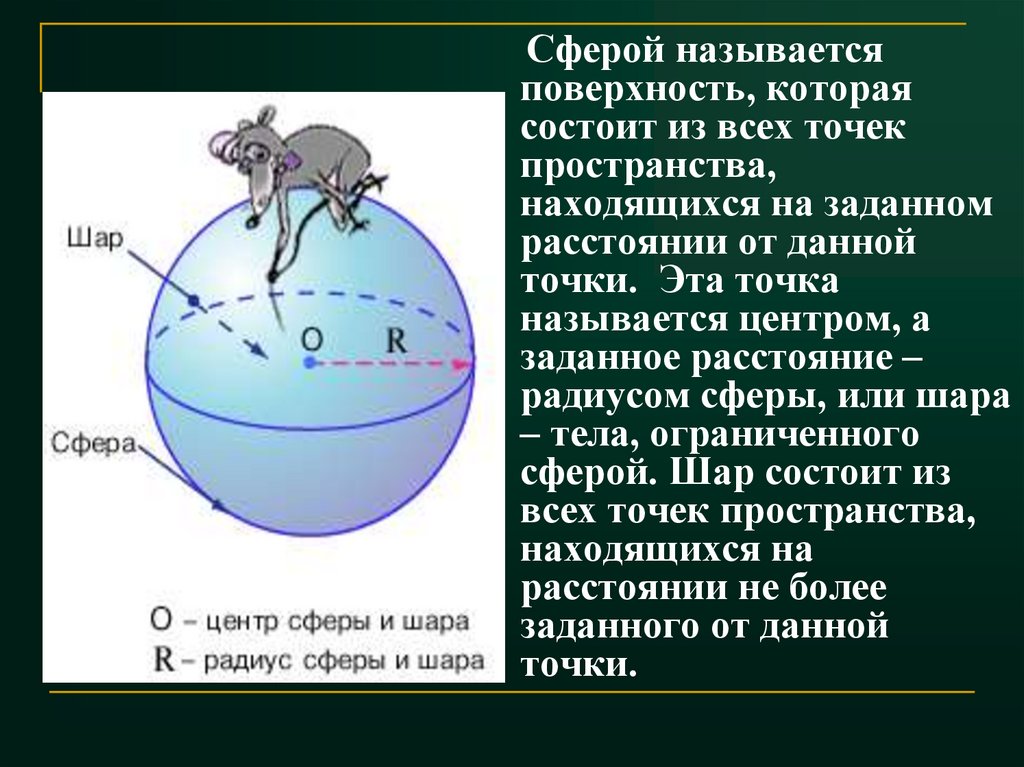
Сферой называется
поверхность, которая
состоит из всех точек
пространства,
находящихся на заданном
расстоянии от данной
точки. Эта точка
называется центром, а
заданное расстояние –
радиусом сферы, или шара
– тела, ограниченного
сферой. Шар состоит из
всех точек пространства,
находящихся на
расстоянии не более
заданного от данной
точки.

5.

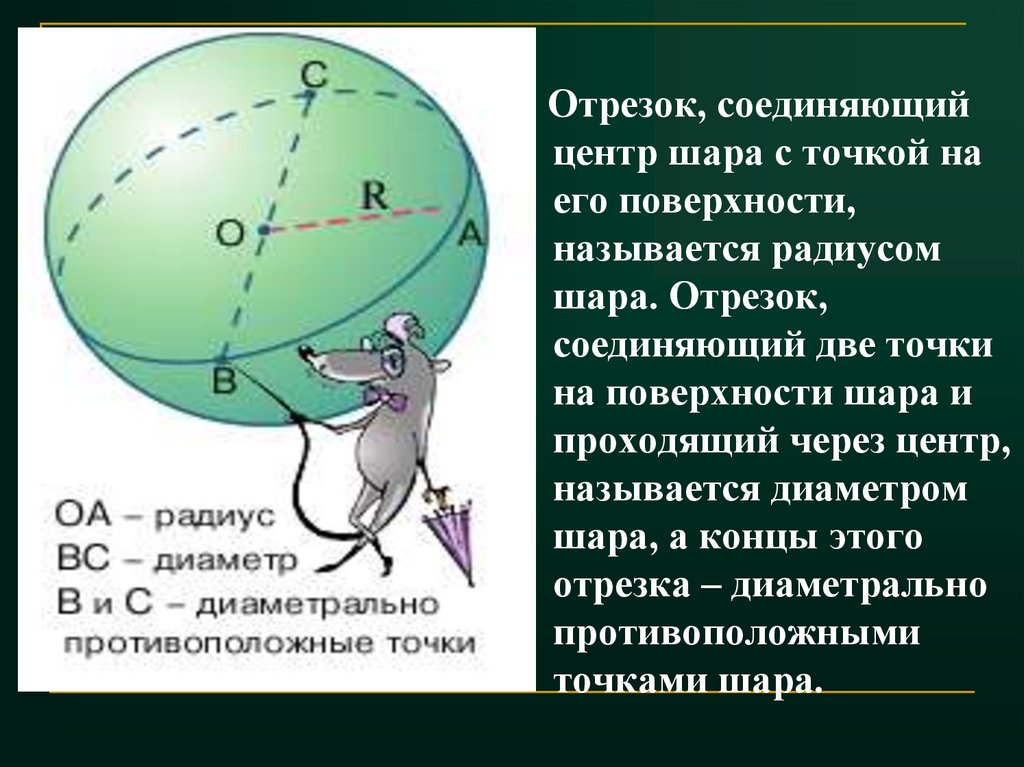
Отрезок, соединяющий
центр шара с точкой на
его поверхности,
называется радиусом
шара. Отрезок,
соединяющий две точки
на поверхности шара и
проходящий через центр,
называется диаметром
шара, а концы этого
отрезка – диаметрально
противоположными
точками шара.

6. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

О- центр сферы
R- радиус сферы
АВ- диаметр сферы
2R=АВ

7. Сферу можно получить вращением полуокружности АСВ вокруг диаметра АВ

8.

Шаром называется тело
ограниченное сферой.
Центр, радиус и диаметр
сферы называются также
диаметром шара.

9.

?
Чему равно
расстояние между
диаметрально
противоположными
точками шара, если
известна удаленность
точки, лежащей на
поверхности шара от
центра?
18

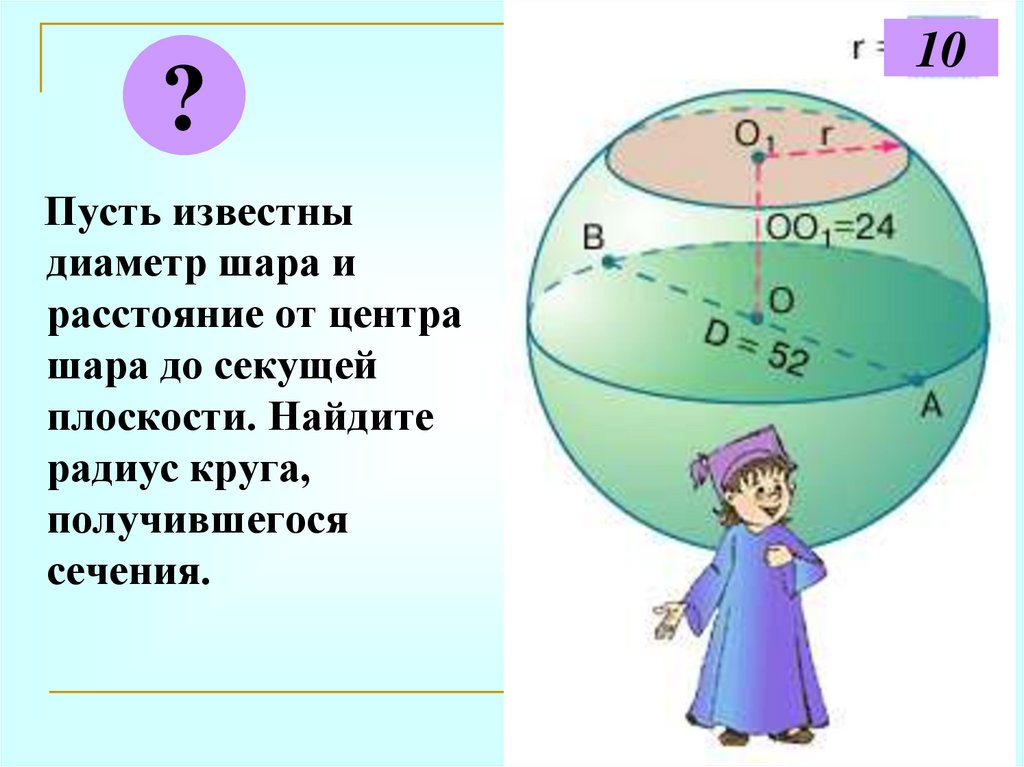
10.

?
Пусть известна
площадь полукруга.
Найдите радиус
шара, который
получается
вращением этого
полукруга вокруг
диаметра.
4

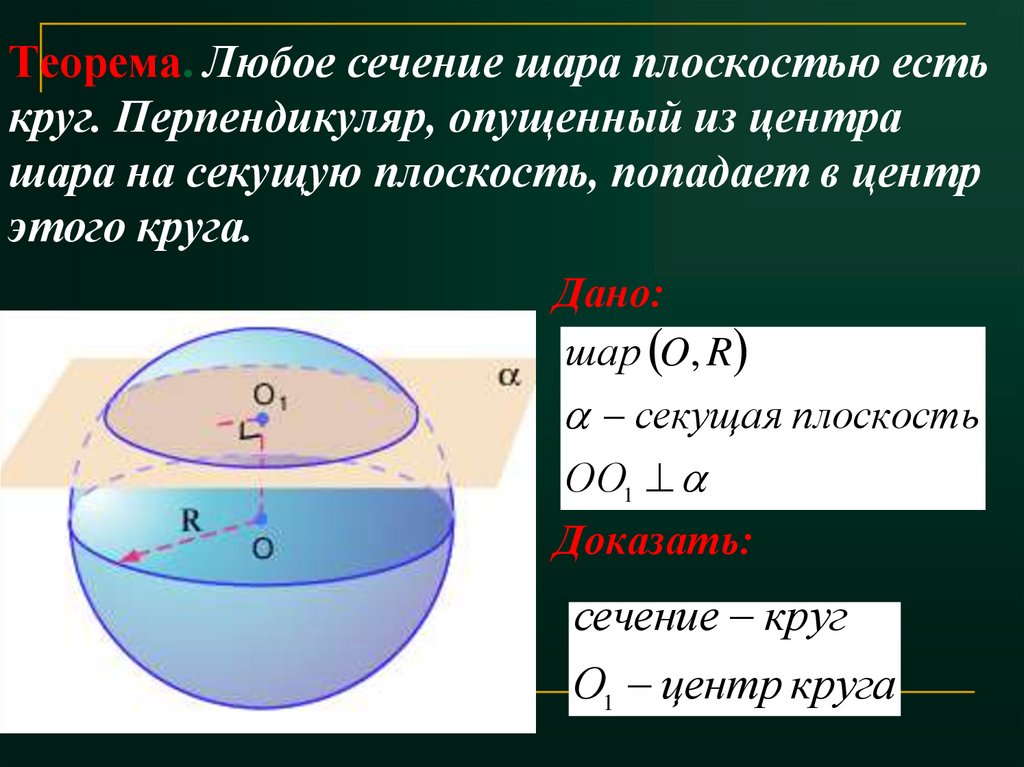
11. Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в

центр
этого круга.
Дано:
шар O, R
секущая плоскость
ОО1
Доказать:
сечение круг
О1 центр круга

12. Доказательство:

Рассмотрим прямоугольный треугольник,
вершинами которого являются центр шара,
основание перпендикуляра, опущенного из центра
на плоскость, и произвольная точка сечения.
OO1 d
ОА R
2
2
2
AO OO1 AO1
2
2
2
R d AO1
AO1 R d
AO1 const
2
2

13. Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме

Пифагора.
О1 К d R
2
2
2
O1 K R d r
2
2
r радиус сечения

14.

?
Пусть известны
диаметр шара и
расстояние от центра
шара до секущей
плоскости. Найдите
радиус круга,
получившегося
сечения.
10

15.

Задана прямоугольная система
координат Оху и дана некоторая
поверхность F, например плоскость или
сфера . Уравнение с тремя переменными
x, у, z называется уравнением
поверхности F и не удовлетворяют
координаты никакой точки , не
лежащей на этой поверхности .
См. далее

16. Выведем уравнение сферы радиуса R с центром С (x1; y1; z1)

M (x; y; z) -
z
произвольная
точка сферы
0
x
y

17. Расстояние от произвольной точки M (x; y; z)до точки С вычисляем по формуле

МС=√(x-x1)2+(y-y1)2+(z-z1)2

18.

Если точка М лежит на данной
сфере , то МС=R, или МС2=R2 т.е.
координаты точки М удовлетворяют
уравнению:
R2=(x-x1)2+(y-y1)2+(z-z1)2
Если точка М не лежит на данной
сфере , то МС2= R2 т.е. координаты
точки М не удовлетворяют данного
уравнения.

19. В прямоугольной системе координат уравнение сферы радиуса R с центром С (x1; y1; z1) имеет вид

2
2
2
2
R =(x-x1) +(y-y1) +(z-z1)

20. Взаимное расположение сферы и плоскости

Исследуем взаимное расположение
сферы и плоскости в зависимости от
соотношения между радиусом сферы
и расстоянием от её центра до
плоскости.

21. Взаимное расположение сферы и плоскости

z
z
C
z
R
C
O
y
x
C
O
2
2
d<R,r= R-d
x
d=R
O
y
x
d>R
См. далее
y

22. Пусть радиус сферы - R, а расстояние от её центра до плоскости a - d

Введём систему координат, так чтобы
плоскость Оху совпадала с плоскостью
α ,а центр сферы лежал по Оz , тогда
уравнение плоскости α :z=0, а
уравнение сферы с учётом (С имеет
координаты (0;0;d) )
2
2
2
2
х +у +(z-d) =R

23. z=0 х2+у 2+(z-d)2=R2

Составим систему уравнений :
z=0
2
2
2
2
х +у +(z-d) =R
Подставив z=0 во второе
уравнение , получим :
2
2
2
2
х +у =R -d

24. Возможны три случая :

тогда R2-d2>0,
и уравнение
х2+у 2=R2-d2 является уравнением
окружности r = √R2-d2 с центром в
точке О на плоскости Оху.
В данном случае сфера и плоскость
пересекаются по окружности.
1) d<R,

25. Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность .

26. Ясно, что сечение шара плоскостью является круг.

Если секущая плоскость проходит через центр шара,
то d=0 и в сечении получается круг радиуса R, т.е.
круг , радиус которого равен радиусу шара. Такой
круг называется большим кругом шара.

27.

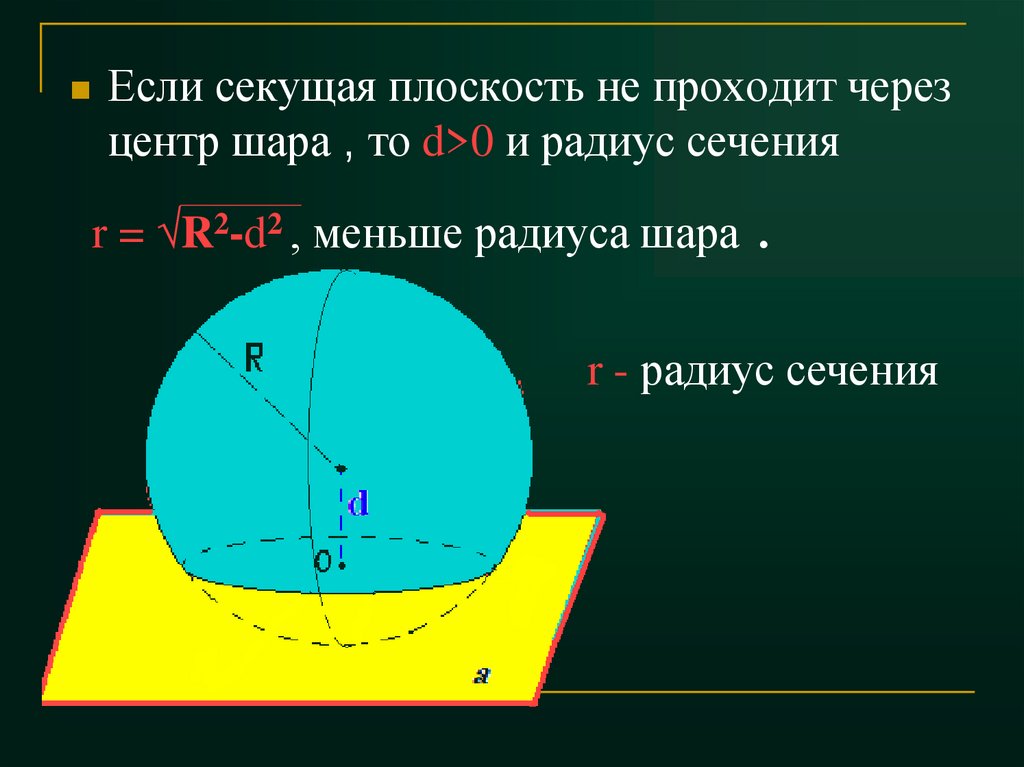
Если секущая плоскость не проходит через
центр шара , то d>0 и радиус сечения
r = √R2-d2 , меньше радиуса шара .
r - радиус сечения

28.

2) d=R,тогда R2-d2=0,
и уравнению
удовлетворяют только
х=0, у=0,
а значит
О(0;0;0)удовлетворяют
обоим уравнениям ,т.е.
О- единственная общая
точка сферы и плоскости
.

29. Итак, если расстояние от центра сферы до плоскости равно радиусу сферы , то сфера и плоскость имеют только одну общую точку.

30.

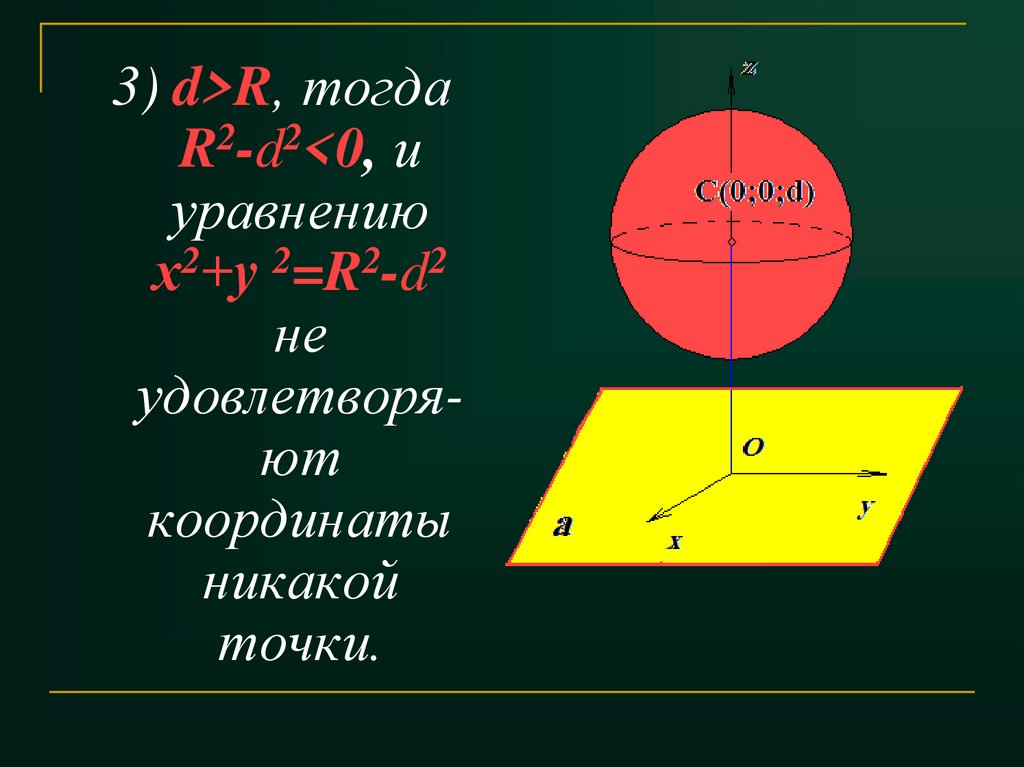
3) d>R, тогда
R2-d2<0, и
уравнению
х2+у 2=R2-d2
не
удовлетворяют
координаты
никакой
точки.

31. Следовательно, если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

32. Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

r R d
2
2
d1 OO1
d 2 OO2
r1 r2
d1 d 2

33.

Наибольший радиус
сечения получается,
когда плоскость
проходит через центр
шара. Круг,
получаемый в этом
случае, называется
большим кругом.
Большой круг делит
шар на два полушара.

34.

?
В шаре, радиус
которого известен,
проведены два
больших круга.
Какова длина их
общего отрезка?
12

35.

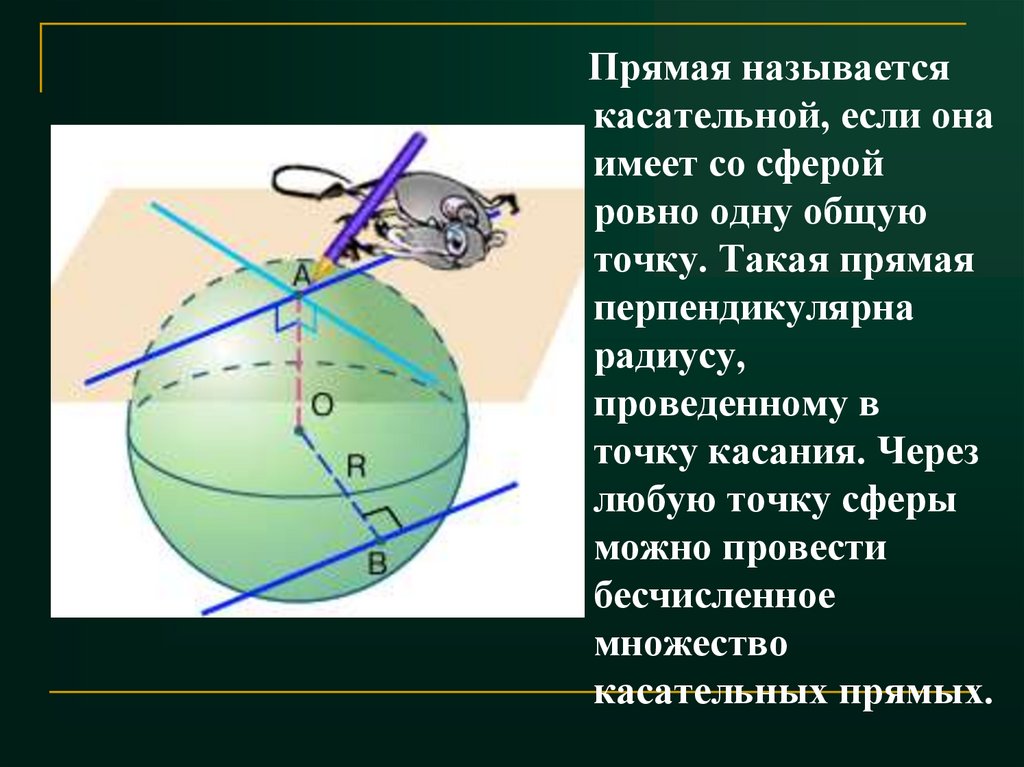
Прямая называется
касательной, если она
имеет со сферой
ровно одну общую
точку. Такая прямая
перпендикулярна
радиусу,
проведенному в
точку касания. Через
любую точку сферы
можно провести
бесчисленное
множество
касательных прямых.

36.

?
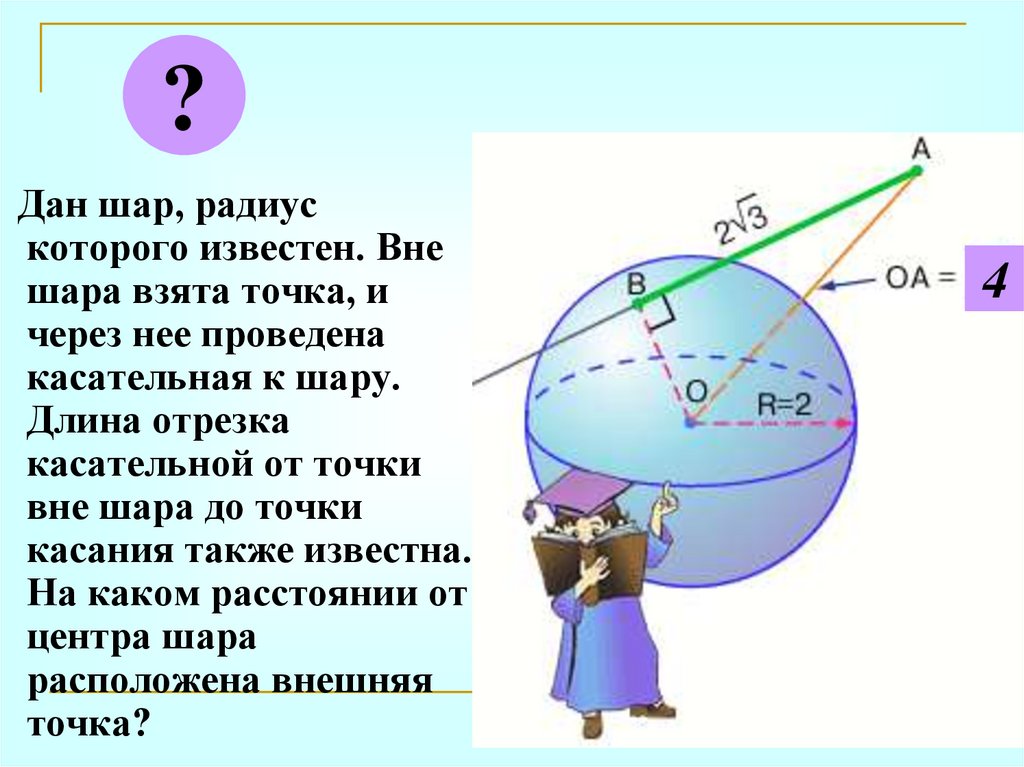
Дан шар, радиус
которого известен. Вне
шара взята точка, и
через нее проведена
касательная к шару.
Длина отрезка
касательной от точки
вне шара до точки
касания также известна.
На каком расстоянии от
центра шара
расположена внешняя
точка?
4

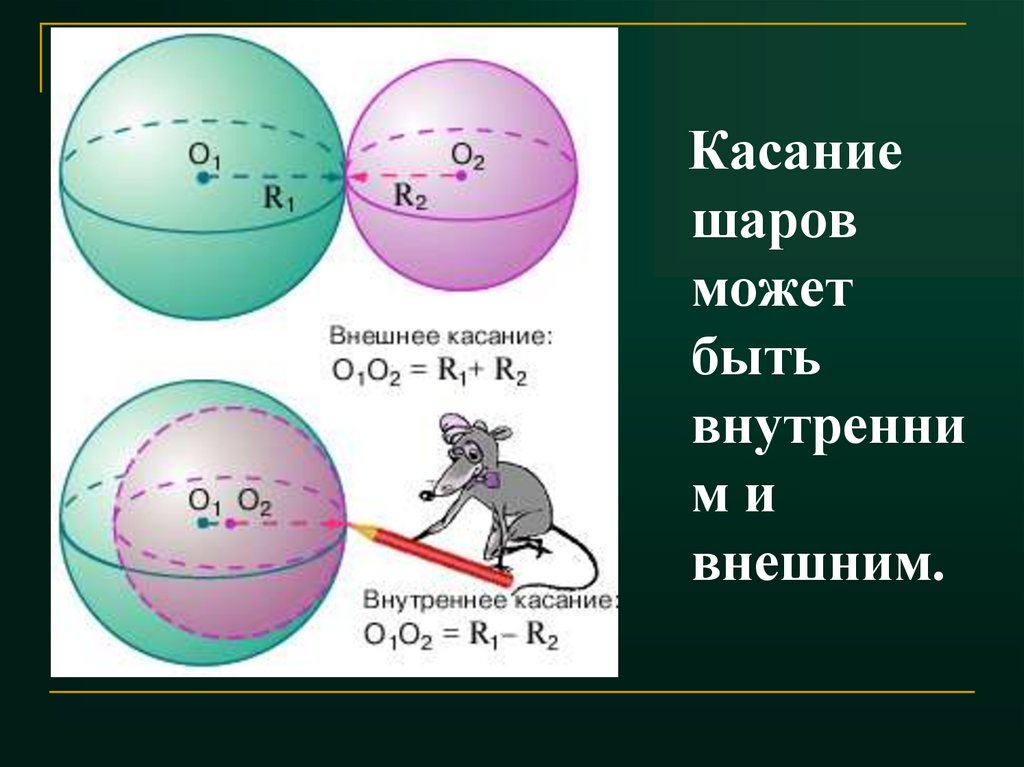
37. Взаимное расположение двух шаров.

Если два шара или сферы
имеют только одну
общую точку, то говорят,
что они касаются. Их
общая касательная
плоскость
перпендикулярна линии
центров (прямой,
соединяющей центры
обоих шаров).

38.

Касание
шаров
может
быть
внутренни
ми
внешним.

39.

Две сферы
пересекаются по
окружности.
Линия центров
перпендикулярна
плоскости этой
окружности и
проходит через ее
центр.

40. Вписанная и описанная сферы.

Сфера (шар)
называется
описанной около
многогранника,
если все вершины
многогранника
лежат на сфере.

41.

?
Какой
четырехугольник
может лежать в
основании пирамиды,
вписанной в сферу?

42.

Сфера называется
вписанной в
многогранник, в
частности, в
пирамиду, если она
касается всех
граней этого
многогранника
(пирамиды).

43.

В основании треугольной
пирамиды лежит равнобедренный Задача.
треугольник, основание и боковые
стороны известны. Все боковые
ребра пирамиды равны 13. Найти
радиусы описанного и вписанного
шаров.
Дано: АВ 8
АС СВ 4 5
SA SB SC 13
Найти:
r вписанного шара
R описанного шара

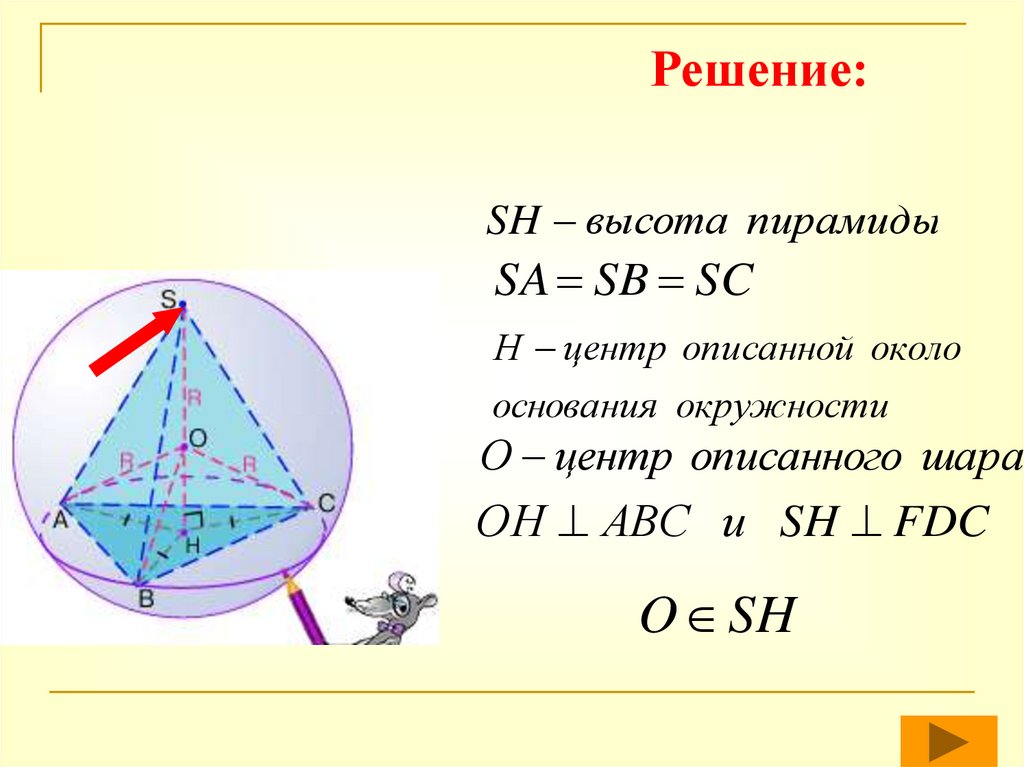
44.

Решение:
SH высота пирамиды
SA SB SC
Н центр описанной около
основания окружности
О центр описанного шара
ОН АВС и SH FDC
O SH

45. I этап. Нахождение радиуса вписанного шара

1) Центр описанного шара удален от всех
вершин пирамиды на одинаковое
расстояние, равное радиусу шара, и в
частности, от вершин треугольника
АВС. Поэтому он лежит на
перпендикуляре к плоскости основания
этого треугольника, который
восстановлен из центра описанной
окружности. В данном случае этот
перпендикуляр совпадает с высотой
пирамиды, поскольку ее боковые ребра
равны.

46. 2) Вычислим радиус описанной около основания окружности.

Решение:
2) Вычислим радиус описанной около основания
окружности.
СК
4 5 4 8
2
2
Из АНК :
НК СК R1 8 R1
R1 5

47. 3) Найдем высоту пирамиды.

3) Найдем высоту пирамиды.Решение:
Из SAH :
SH 13 5 12
2
2

48. 4) Радиус описанного шара найдем из треугольника, образованного радиусом шара и частью высоты, прилежащей к основанию пирамиды.

Решение:
4) Радиус описанного шара найдем из
треугольника, образованного радиусом шара и
частью высоты, прилежащей к основанию
Из АНО :
пирамиды.
ОН 12 R
R 5 12 R
2
2
2
R 2 25 144 R 2 24 R
169
1
R
7
24
24

49.

Решение:
II этап.
Нахождение радиуса вписанного шара.
Соединим центр
вписанного шара со всеми
Пирамиды
:
вершинами пирамиды,
тем самым
мы, разделим
ОSAB
ее на несколько меньших
OSBC
,
пирамид. В данном случае
OSAC
,
их четыре.
Высоты
всех
пирамид
одинаковы и
OABC
равны радиусу вписанного
шара, а основания – это
грани исходной пирамиды.

50. 1) Найдем площадь каждой грани пирамиды и ее полную поверхность.

Решение:
1) Найдем площадь каждой грани
пирамиды и ее полную поверхность.
1
S ABC AB CK 32
2
1
S SBC BC SL 2 5 149
2
S SAC S SBC 2 5 149
1
S SAB AB SK 4 153
2
S полн 32 4 5 149 4 153

51. 2) Вычислим объем пирамиды и радиус вписанного шара.

SH 12
Rопис 7
1
24
Решение:
S ABC 32
1
V SH S ABC 128
3
3V
96
r
S полн 8 745 153
96
r
8 745 153