Шар. Сфера

1. Шар. Сфера.

2. Основные вопросы:

2

3.

Шар или
сфера?

4.

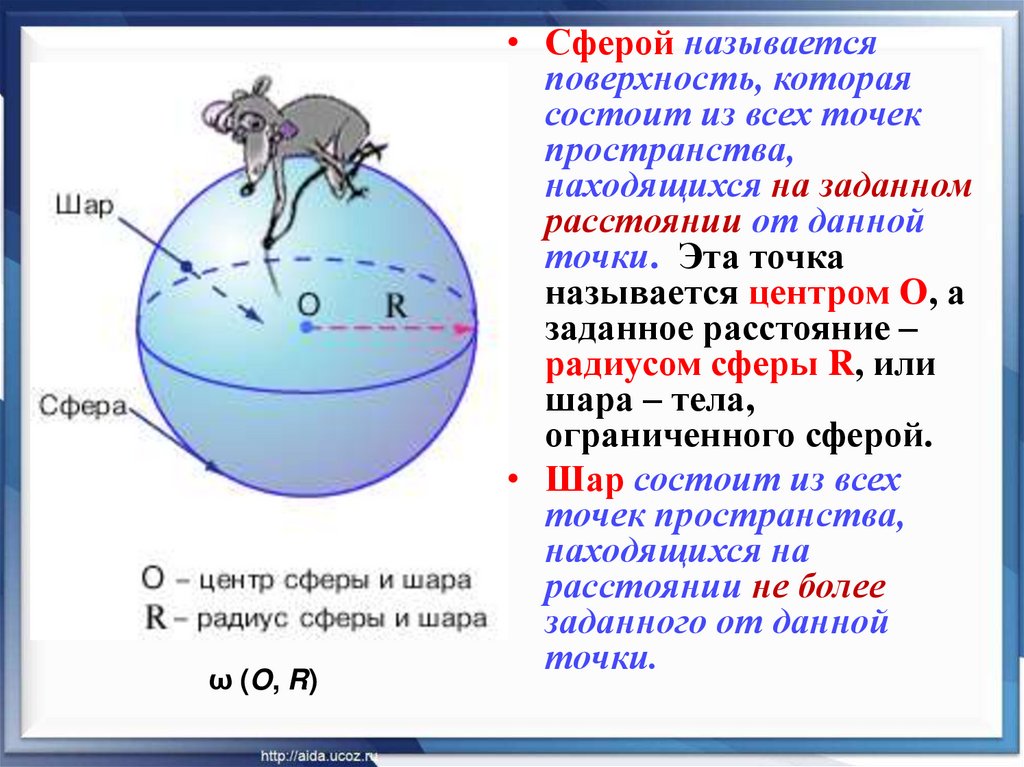
ω (O, R)
• Сферой называется
поверхность, которая
состоит из всех точек
пространства,
находящихся на заданном
расстоянии от данной
точки. Эта точка
называется центром О, а
заданное расстояние –
радиусом сферы R, или
шара – тела,
ограниченного сферой.
• Шар состоит из всех
точек пространства,
находящихся на
расстоянии не более
заданного от данной
точки.

5.

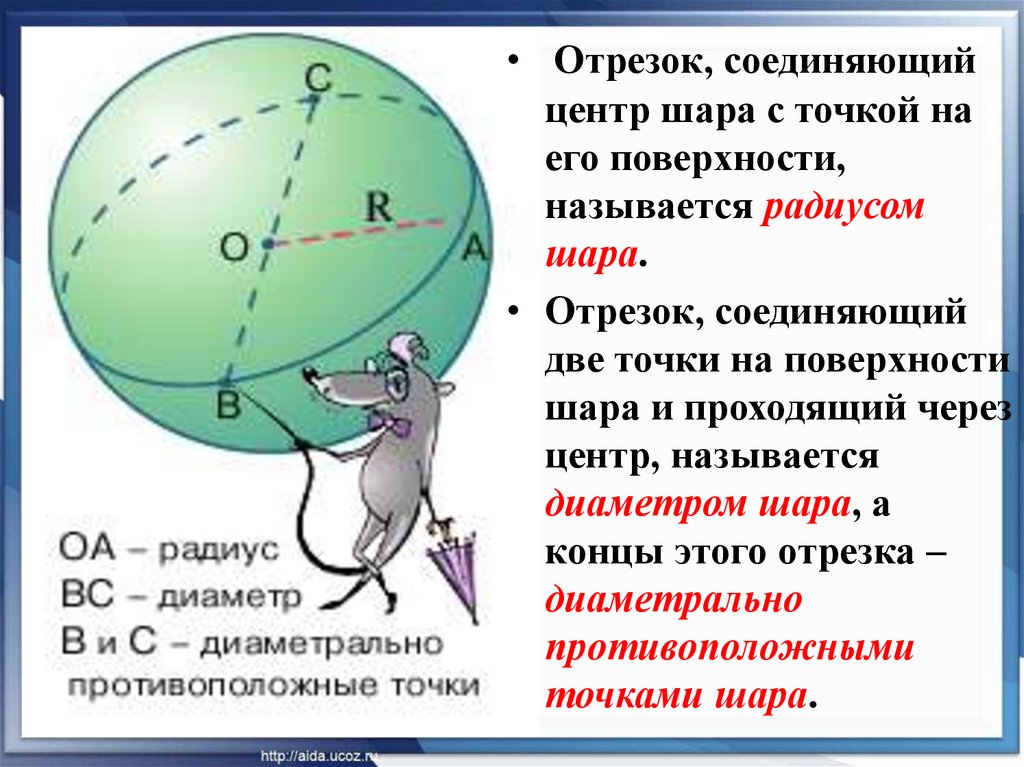
• Отрезок, соединяющий
центр шара с точкой на
его поверхности,
называется радиусом
шара.
• Отрезок, соединяющий
две точки на поверхности
шара и проходящий через
центр, называется
диаметром шара, а
концы этого отрезка –
диаметрально
противоположными
точками шара.

6.

Шар можно
рассматривать как
тело, полученное от
вращения полукруга
вокруг диаметра как
оси.

7. Уравнение сферы.

Выведем уравнение сферы радиуса R с
центром С (х0; у0; z0)
Расстояние от произвольной точки М (х;
у; z) до точки С вычисляется по формуле:
В прямоугольной системе
координат уравнение сферы
радиуса R с центром С (х0; у0; z0)
имеет вид:

8.

Уравнение сферы
Центр
r
(x–3)2 +(y–2)2 +(z – 1)2=16 C(3;2;1)
r=4
(x–1)2+(y+2)2+(z+5)2 = 4
C(1;-2;-5)
r=2
(x+5)2+(y–3)2 + z2 = 25
C(-5;3;0)
(x – 1 )2 + y 2 + z 2 = 8
C(1;0;0)
r=5
r= 8
x2 +(y+2)2 +(z+8)2 = 2
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
x 2 + y 2 + z 2= 9
(x–3 )2+(y–2)2 + z 2 = 0,09
C(3; 2;0)
(x+7)2+(y–5)2 +(z+1)2 = 2,5 C(-7; 5;-1)
1
2
2
2
C(0;-4;9)
x +(y+4) + (z+4) = 64
r = 0,3
r = 2,5
5
r= 2

9. Взаимное расположение сферы и плоскости

• Если расстояние
от центра сферы
до плоскости
меньше радиуса
сферы, то
сечение сферы
плоскостью есть
окружность.
d<R
9

10. Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку. d=R

• Если расстояние от
центра сферы до
плоскости равно
радиусу сферы, то
сфера и плоскость
имеют только одну
общую точку.
d=R

11. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек. d>R

• Если расстояние от
центра сферы до
плоскости больше
радиуса сферы, то
сфера и плоскость не
имеют общих точек.
d>R

12. Плоскость и прямая, касательные к сфере.

Плоскость, имеющая со
сферой только одну
общую точку,
называется
касательной
плоскостью.
Касательная плоскость
перпендикулярна
радиусу, проведенному
в точку касания.

13.

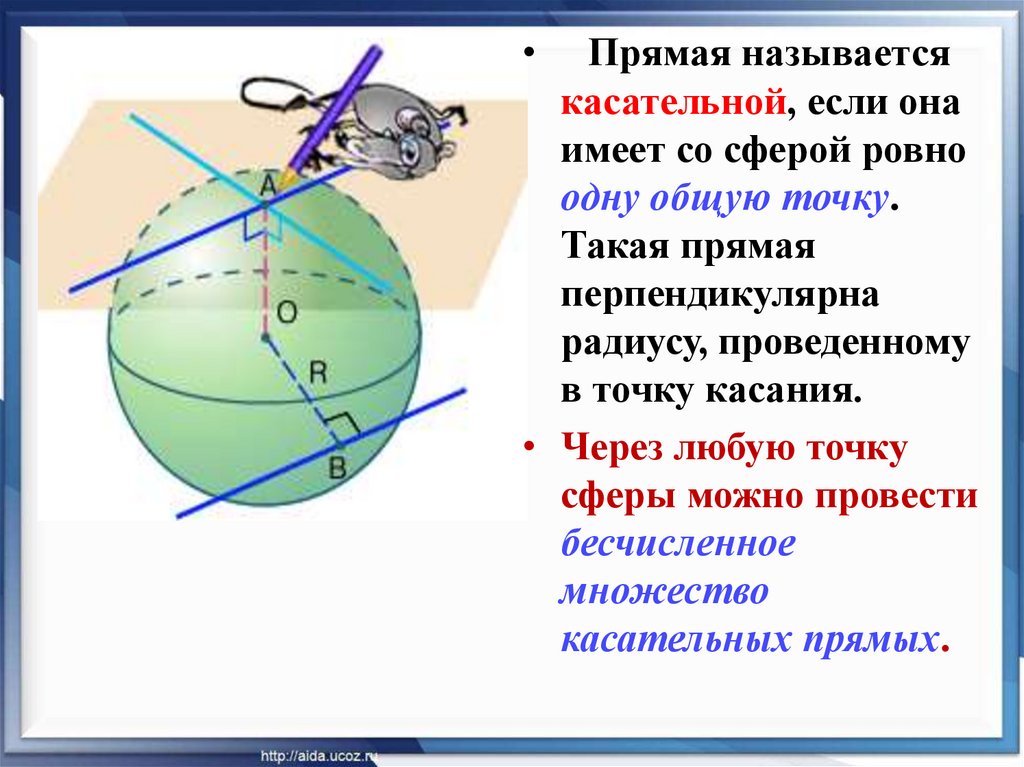
Прямая называется
касательной, если она
имеет со сферой ровно
одну общую точку.
Такая прямая
перпендикулярна
радиусу, проведенному
в точку касания.
• Через любую точку
сферы можно провести
бесчисленное
множество
касательных прямых.

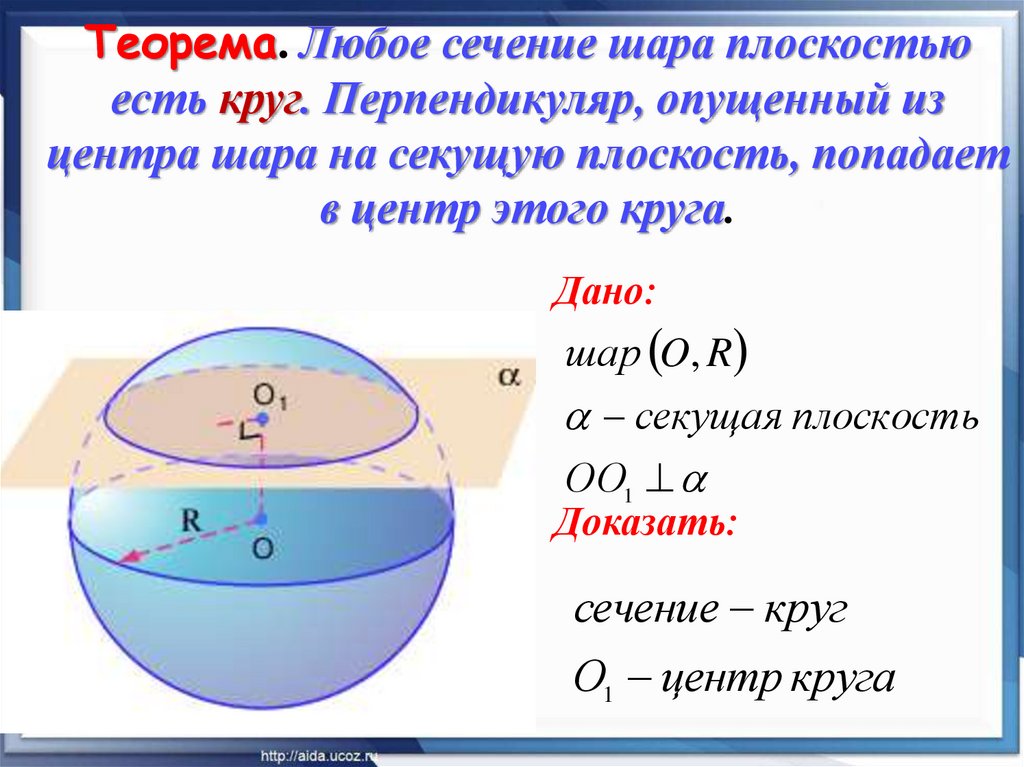
14. Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в

центр этого круга.
Дано:
шар O, R
секущая плоскость
ОО1
Доказать:
сечение круг
О1 центр круга

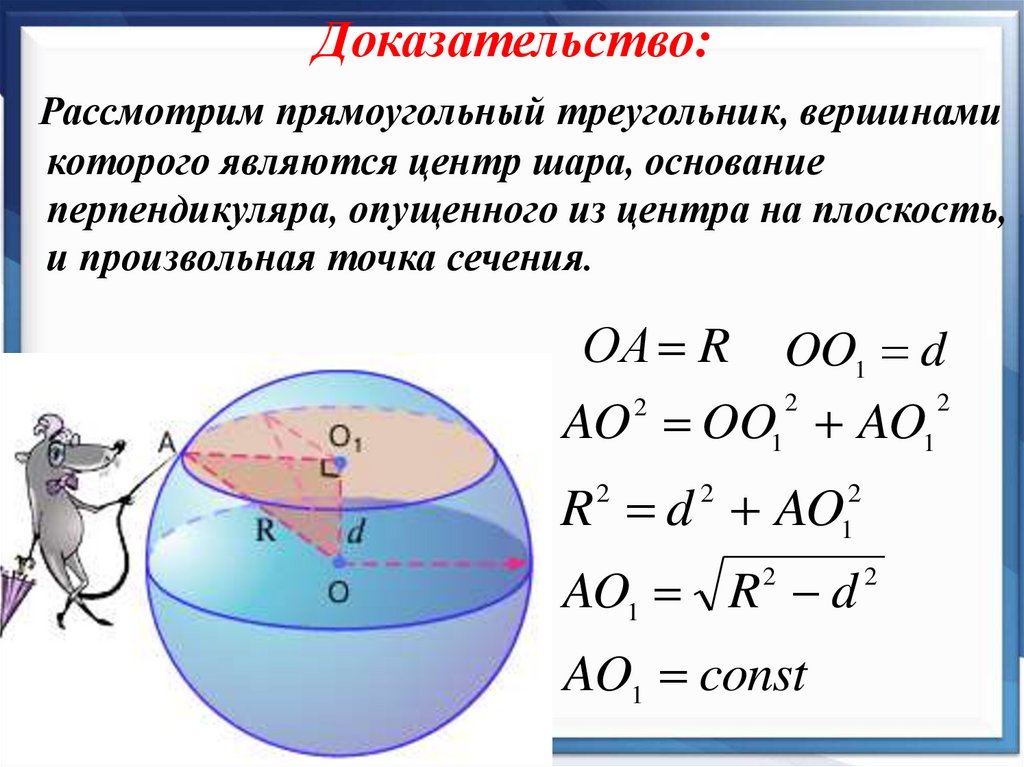
15. Доказательство:

Рассмотрим прямоугольный треугольник, вершинами
которого являются центр шара, основание
перпендикуляра, опущенного из центра на плоскость,
и произвольная точка сечения.
ОА R OO1 d
2
2
2
AO OO1 AO1
R d AO
2
2
2
1
AO1 R d
2
AO1 const
2

16. Следствие. Если известны радиус шара и расстояние от центра шара до плоскости сечения, то радиус сечения вычисляется по теореме

Пифагора.
О1 К d R
2
2
2
O1 K R d r
2
2
r радиус сечения

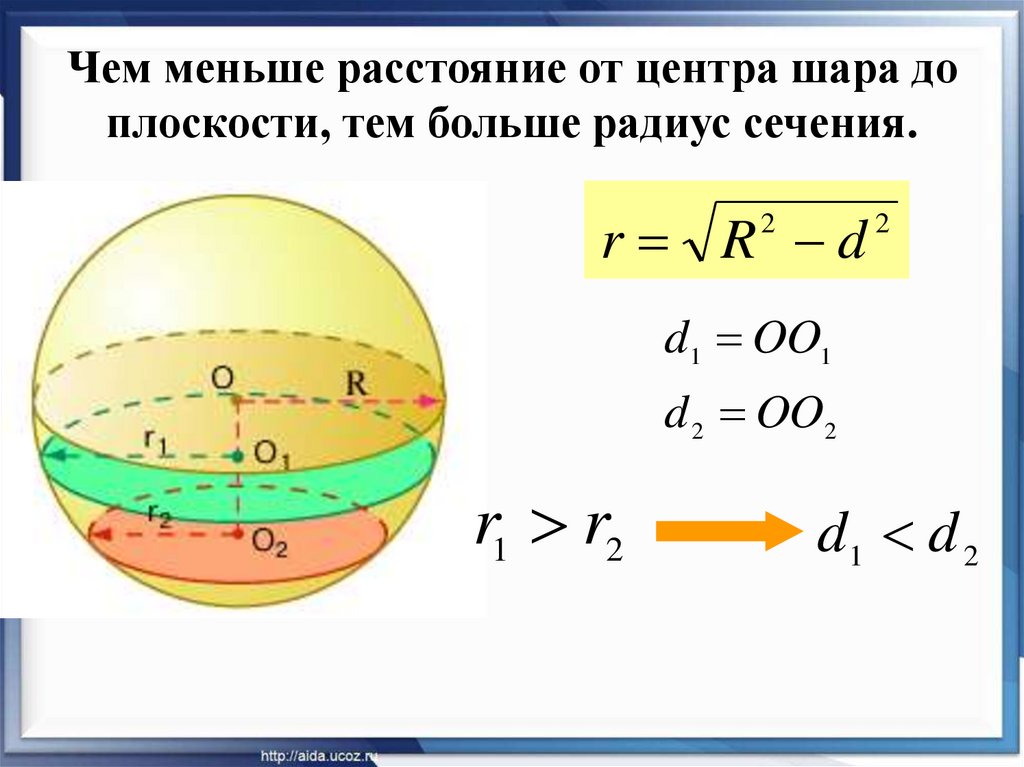
17. Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.

r R d
2
2
d1 OO1
d 2 OO2
r1 r2
d1 d 2

18.

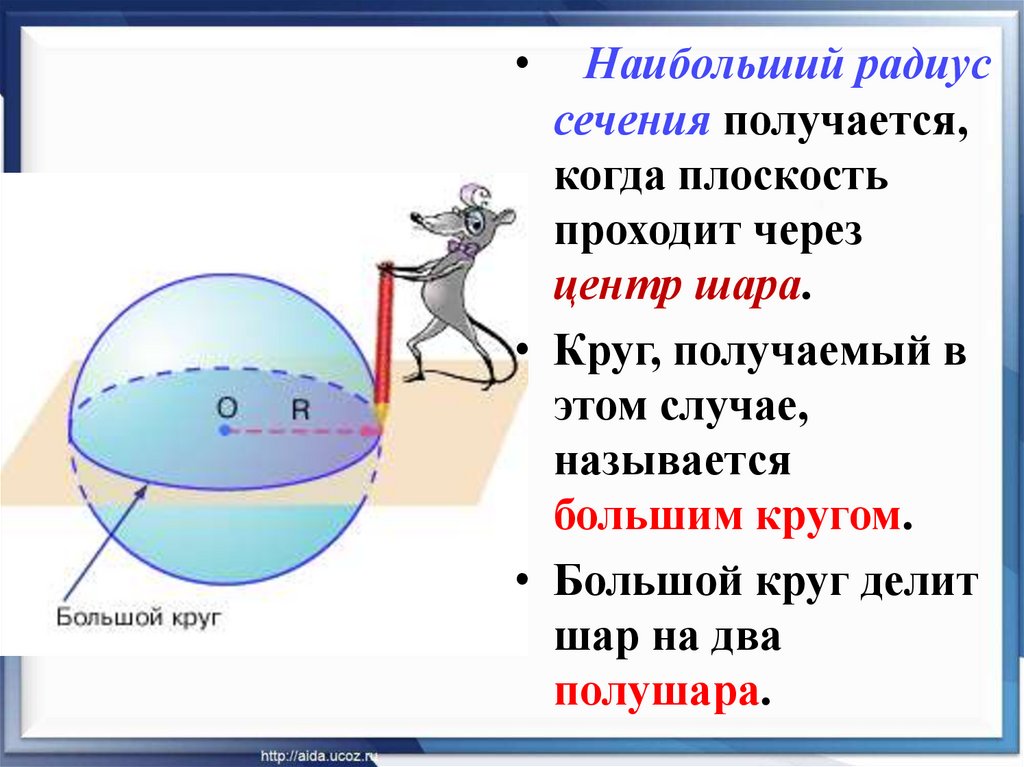
Наибольший радиус
сечения получается,
когда плоскость
проходит через
центр шара.
• Круг, получаемый в
этом случае,
называется
большим кругом.
• Большой круг делит
шар на два
полушара.

19. Взаимное расположение двух шаров.

Если два шара или
сферы имеют только
одну общую точку, то
говорят, что они
касаются. Их общая
касательная плоскость
перпендикулярна линии
центров (прямой,
соединяющей центры
обоих шаров).

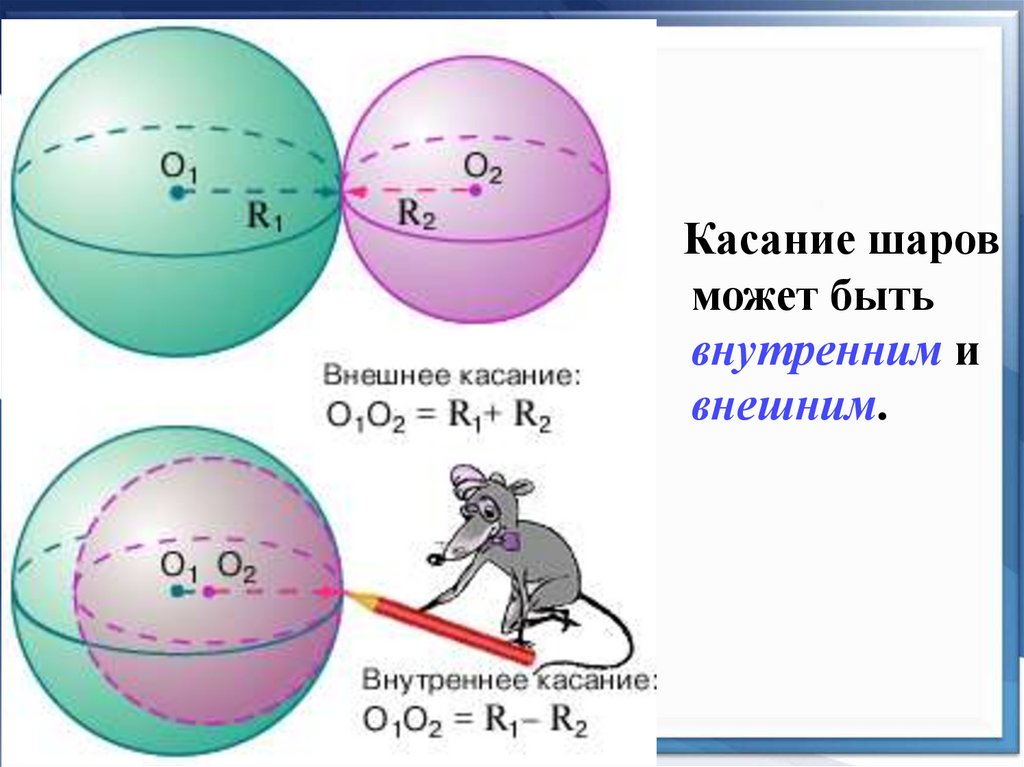
20.

Касание шаров
может быть
внутренним и
внешним.

21. Площадь сферы

• Площадь S сферы
радиуса R
вычисляется по
формуле:
21

22.

22

23.

23

24.

24

25.

25

26.

Стороны треугольника 13см, 14см и
15см. Найти расстояние от плоскости
треугольника до центра шара,
касающегося сторон треугольника.
Радиус шара равен 5 см.
Дано:
АВ 15см
АС 14см
ВС 13см
Найти:
d O, FDC

27.

Решение:
Сечение сферы, проходящее через точки
касания, - это вписанная в треугольник АВС
окружность.

28.

Решение:
Вычислим радиус окружности, вписанной в
треугольник.
S p p a p b p c
14 15 13
p
21
2
S 84
S r p
S 84
r 4
p 21

29.

Решение:
Зная радиус сечения и радиус шара, найдем
искомое расстояние.
Из ОО1 К :
R r d
2
2
2
d R r 3
2
2
d O, ABC 3см

30. Задача

30

31. Решение:

31

32. Задача

Решение:
32

33. Задача

Стороны треугольника 13 см, 14 см, 15 см.
Найти расстояние от плоскости
треугольника до центра шара,
касательного к сторонам треугольника.
Радиус шара 5 см.
33

34. Решение:

34

35. Решение:

35

36. Задача

Решение:
36

37. Задача

Решение:
37

38. Задача

38

39. Решение:

39

40. Задача

40

41. Решение:

41

42. ДОМАШНЕЕ ЗАДАНИЕ:

• Учебник Геометрия /Атанасян/
гл.6 §3 ( п.58 – 60, 62) ,вопросы: 7 – 10
(стр.135 - 136)
42

43.

43