Similar presentations:
Метод алгебраического сложения
1.
Метод алгебраическогосложения
2.
Графический способВыразить у через х в каждом
уравнении.
Построить в одной системе
координат график каждого уравнения.
Определить координаты точек
пересечения.
Записать ответ.
3.
Способ подстановкиИз какого-либо уравнения выразить
одну переменную через другую.
Подставить полученное выражение
для переменной в другое уравнение и
решить его.
Вычислить значение второй
переменной.
Записать ответ: (х ; у) .
4.
Способ сложенияУмножить почленно уравнения системы,
подбирая множители так, чтобы
коэффициенты при одной из переменных
стали противоположными числами.
Сложить почленно левые и правые
части уравнений системы.
Решить получившееся уравнение с одной
переменной.
Подставить значение найденной
переменной в одно из уравнений системы
и найти значение другой переменной.
Записать ответ: (х; у) .
5.
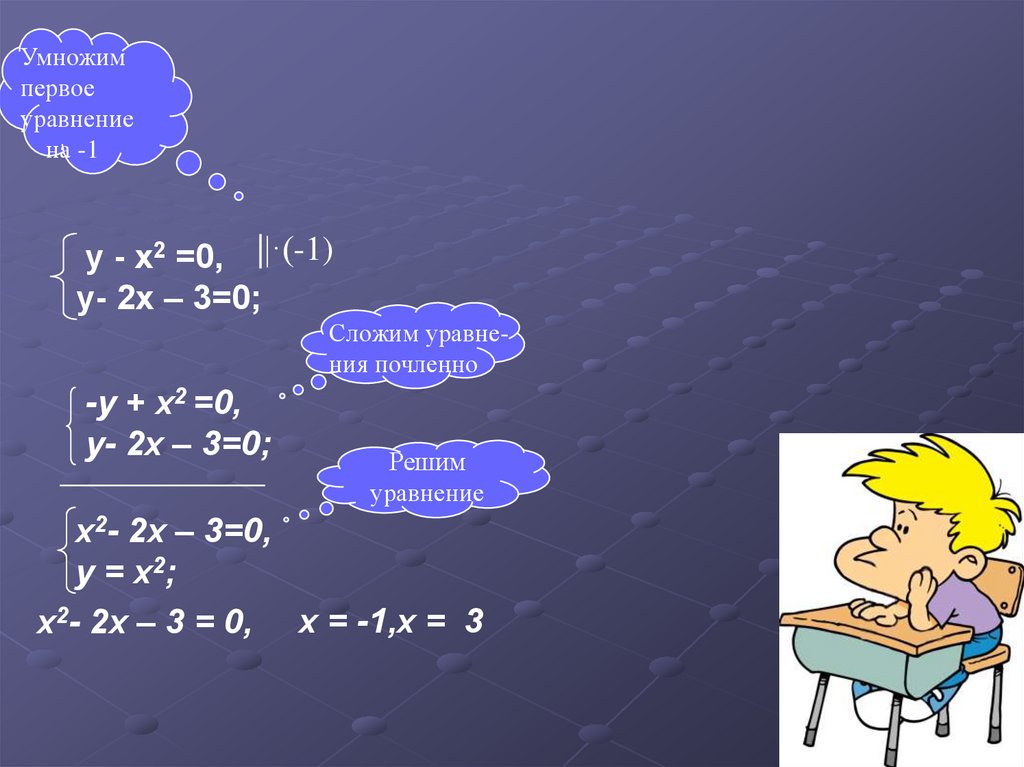
Умножимпервое
уравнение
на -1
у - x2 =0, ||·(-1)
у- 2x – 3=0;
Сложим уравнения почленно
-у + x2 =0,
у- 2x – 3=0;
____________
Решим
уравнение
х2- 2x – 3=0,
у = х2;
х2- 2x – 3 = 0, х = -1,х = 3
6.
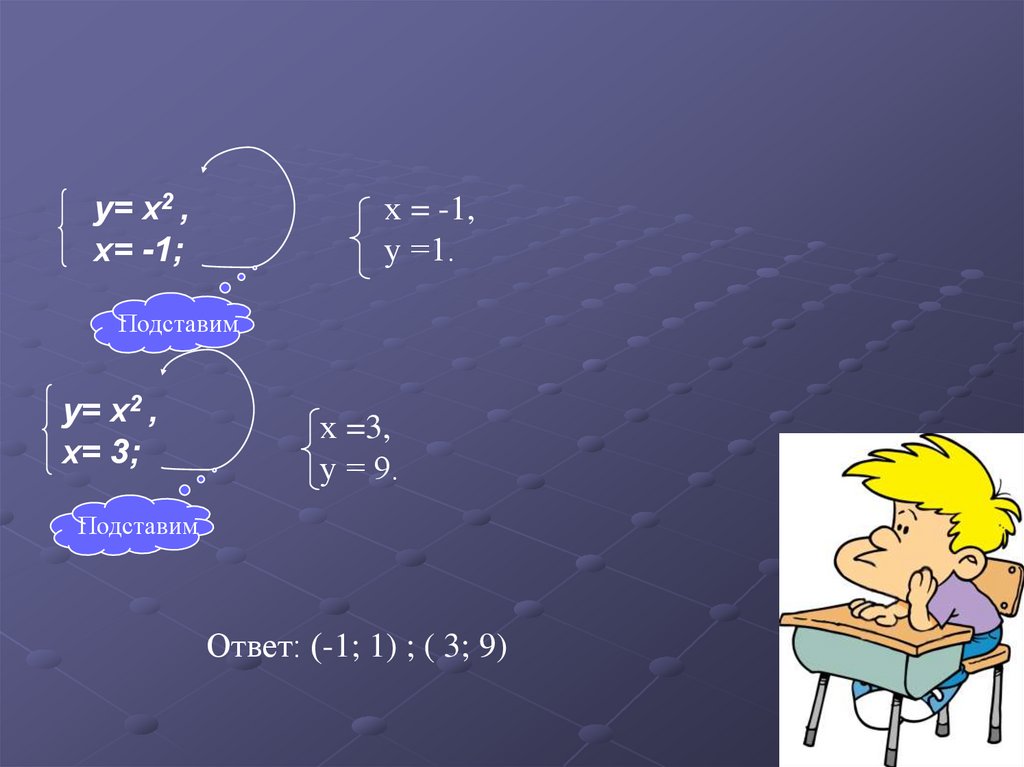
х = -1,у =1.
y= x2 ,
x= -1;
Подставим
y= x2 ,
x= 3;
х =3,
у = 9.
Подставим
Ответ: (-1; 1) ; ( 3; 9)
7.
№ 6.7 (г)│∙ 2
│∙ 7
+
43m = 43
m=1
4 ∙ 1 + 7n = 11
n=1
Ответ: (1; 1)
8.
№ 6.8 (г)+
2х² = 32
х² = 16
х=±4
16 – 2у² = 14
9.
№ 6.8 (г)у² = 1
у= ±1
х=±4
Ответ: (4; 1), (4; - 1),
(- 4; 1), (- 4; - 1)
10.
№ 6.15 (г)+
4х² + 4х = 24
х² + х – 6 = 0
х1 = – 3, х2 = 2
11.
№ 6.15 (г)х1 = – 3
(– 3)² – у² – 3 – у = 6
у² + у = 0
у1 = – 1, у2 = 0
12.
№ 6.15 (г)х2 = 2
2² – у² +2 – у = 6
у² + у = 0
у3 = – 1, у4 = 0
13.
Ответ:(2; 0), (2; – 1),
(– 3; 0), (– 3; – 1)
14.
Домашнее задание№ 6.7 - № 6.8 (а)





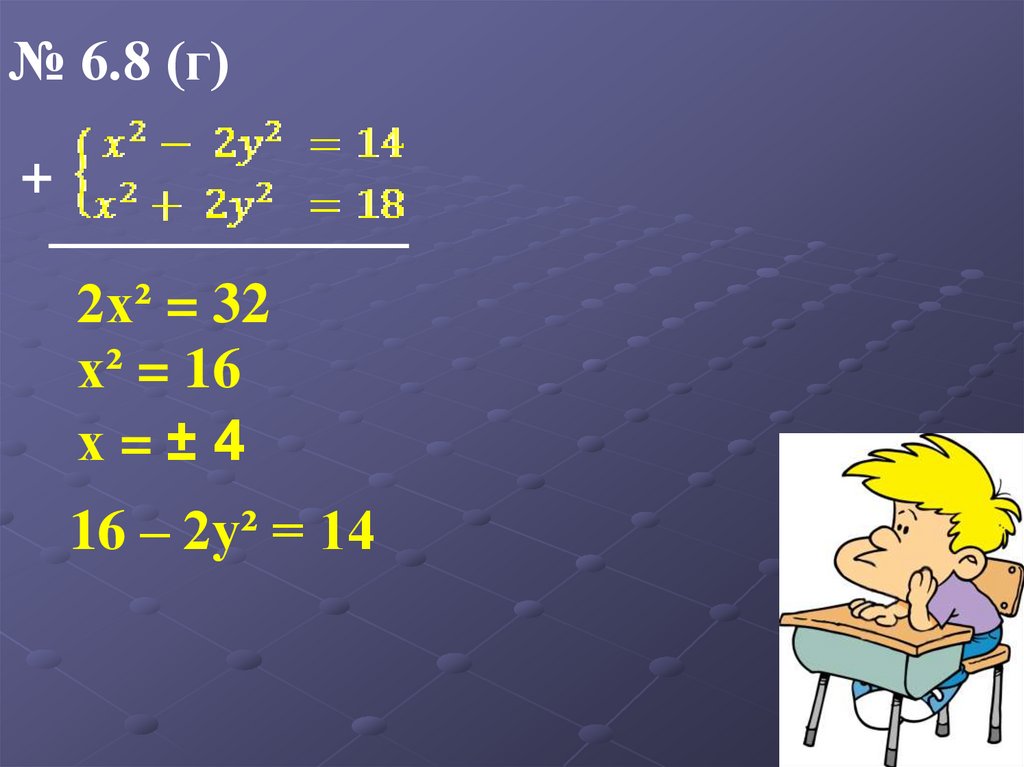






 mathematics
mathematics








