Similar presentations:
Метод мажорант
1. Метод мажорант
МБОУ «Средняя общеобразовательная школа № 77г.Новокузнецк, Кемеровская область
Метод мажорант
Учитель математики
Федорова Татьяна Андреевна
2.
Название метода мажорантпроисходит
от французских слов
«majorer» объявлять большим
«minorer» объявлять меньшим.
3.
Мажорантойданной функции f(х)
на множестве Р, называется
такое число М, что
либо f(х) ≤ М для всех х ϵ Р,
либо f(х) ≥ М для всех х ϵ Р.
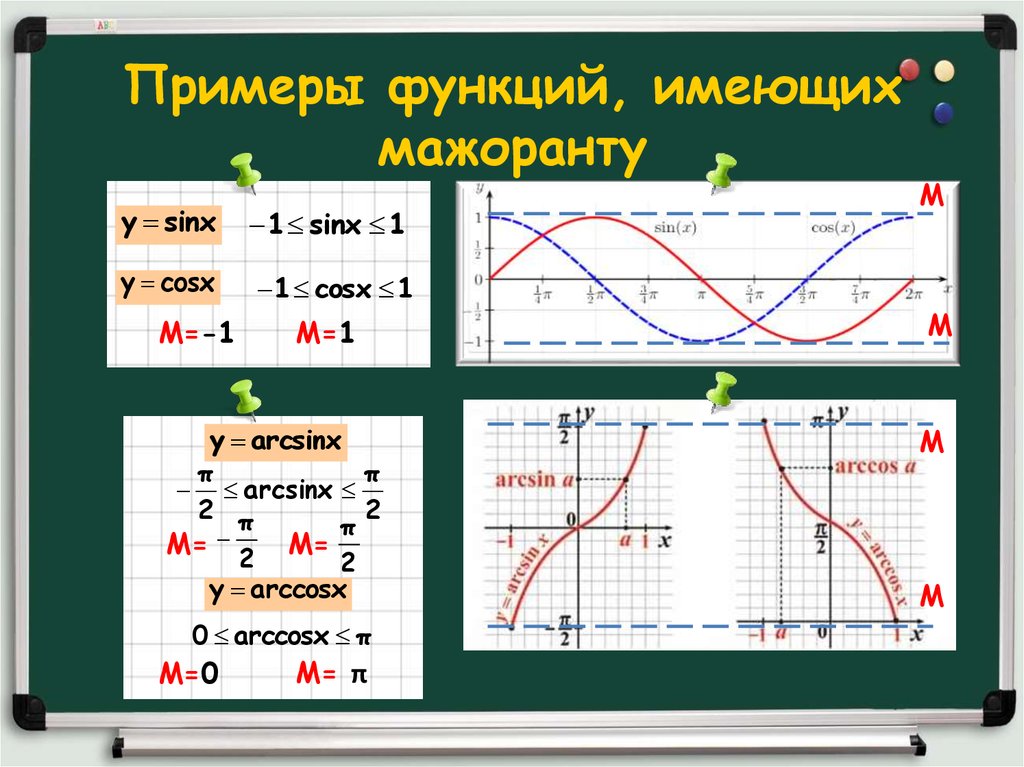
4. Примеры функций, имеющих мажоранту
у sinx1 sinx 1
у cosx
1 cosx 1
М=-1
М=1
у arcsinx
π
π
arcsinx
2 π
2
π
М= 2 М=
2
у arcсosx
0 arccosx π
М=0
М= π
М
М
М
М
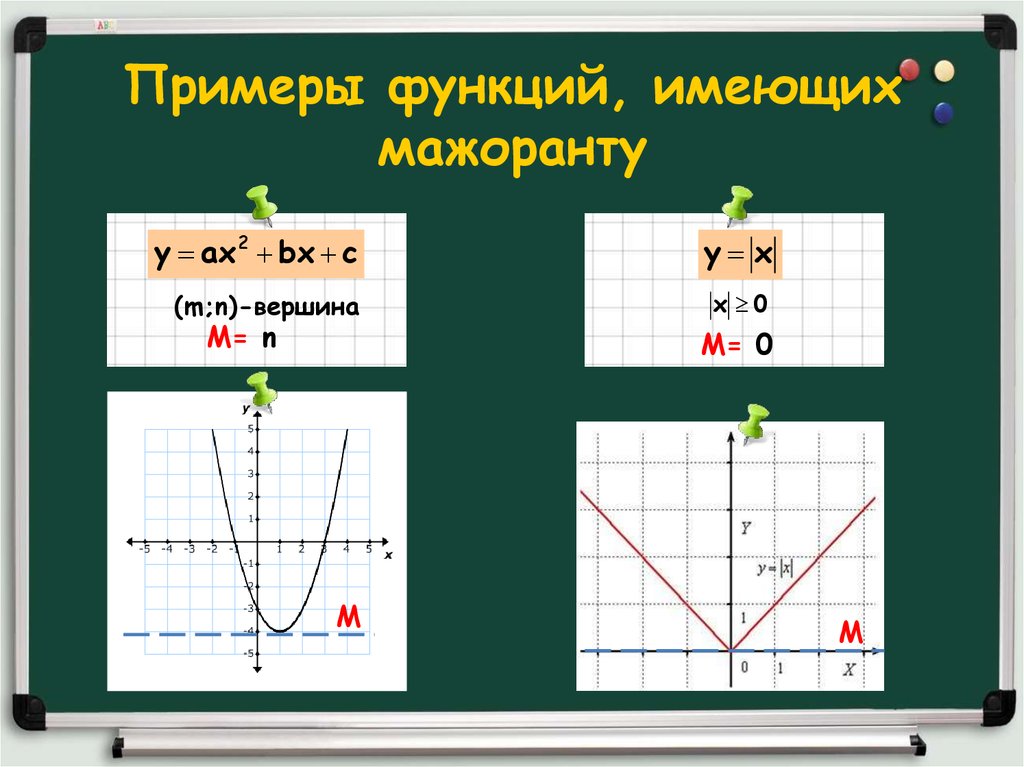
5. Примеры функций, имеющих мажоранту
y ax 2 bx cy x
(m;n)-вершина
x 0
М= n
М= 0
М
М
6.
Чтобы решить уравнение вида f(x)=g(x)или неравенства вида
f(x)≥ g(x), f(x)≤g(x) методом мажорант
Оценить левую часть: f(x)
Оценить правую часть: g(x)
Если f(x)≥М , при этом g(x)≤M ( или f(x)≤М, , при
этом g(x)≥M), составить систему уравнений
f(x)=М,
g(x)= М.
Решить одно из уравнений системы
Выполнить проверку, подставив найденные
корни во второе уравнение системы
7.
Решить уравнение:5
х2 2х 2
4 cos πx
Решение:
Оценим левую часть уравнения:
x 2х 2 (x 2х 1) 1 (x 1) 1 1 5
2
2
2
(х 1)2 1
5
Оценим правую часть уравнения:
-1 сos πx 1
-1 сos πx 1 4 -1 4 сos πx 1 4
3 4 сos πx 5
C одной стороны
5
с другой стороны
Уравнение
5
(х-1)2 1
(х 1)2 1
5
4 сos πx 5
4 cos πx
имеет решение, если
8.
5(х 1)2 1
5,
4 сos πx 5.
Решим первое уравнение системы:
5
(х 1)2 1
(х 1)2 1
51 (х 1)2 1 1
5, 5
(х 1)2 0 х 1
Если х 1, то 4 - cos(π 1) 4 1 5
Решение системы, а значит и уравнения: х=1.
Ответ:
х=1
9.
Решить уравнение:1
2
4
2cosx
cos
2x 5cos3x
2
2
cos x
Решение:
ОДЗ: сosx 0
1
Оценим левую часть уравнения: 2
4 2cosx
2
cos x
1
1
0 сos 2 x 1
1 2
3
2
2
сos x
сos x
-1 сos x 1 -2 2сos x 2 4 - 2 4 2сos x 4 2
2 4 2сos x 6
1
Перемножим два
2
3
4 2сos x 2
2
и
сos
x
неравенства:
10.
12
4 2cosx 6
2
cos x
Оценим правую часть уравнения: cos 2 2x 5cos3x
0 cos 2 2x 1
1 cos3x 1
5 5cos3x 5
Складываем двойные неравенства:
0 cos 2 2x 1
Получим: 5 cos 2 2x 5cos3x 6
5 5cos3x 5
1
C одной стороны 2
4 2cosx 6
2
cos x
2
cos
2x 5cos3x 6
с другой стороны
1
2
4
2cosx
cos
2x 5cos3x
Уравнение 2
2
cos x
имеет решение, если
11.
12
4 2cosx 6,
2
cos x
cos 2 2x 5cos3x 6.
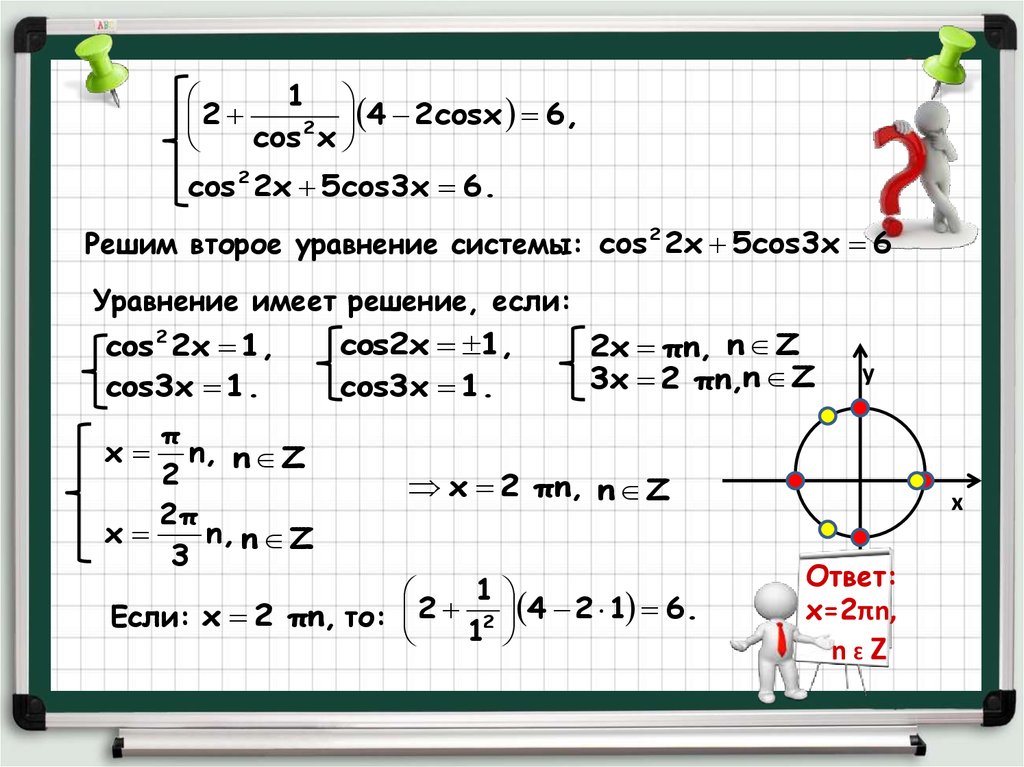
Решим второе уравнение системы: cos 2 2x 5cos3x 6
Уравнение имеет решение, если:
cos 2 2x 1,
cos3x 1.
π
n, n Z
2
2π
x
n, n Z
3
x
cos2x 1,
cos3x 1.
2x πn, n Z
3x 2 πn,n Z
у
x 2 πn, n Z
1
4 2 1 6.
2
Если: x 2 πn, то:
2
1
х
Ответ:
х=2πn,
nƐZ
12.
Решить неравенствоx2 1
3х 2х log2
x
2
Решение:
3
ОДЗ: х ˃ 0
х2 1
х2 1
1
х
х
х х
х
2
1
x
1
Если х ˃0, то х 2 ,тогда log
1 для любых х
2
х
x
из ОДЗ
2
3
Оценим левую часть неравенства: 3х 2х
Для этого введем функцию: у 3х2 2х 3
Преобразуем выражение:
Найдем производную функции: у 6х 6х2
Найдем критические точки: у 0;
х1 0,
6х 6х2 0
х2 1
0
1
13.
01
у(1) 3 12 2 13 1
-наибольшее значение функции
2
x
1
1
C одной стороны 3х2 2х 3 1,с другой стороны log 2
x
Неравенство
x2 1
3х 2х log2
имеет решение, если
x
3x 2 2x 3 1,
x2 1
1.
log 2
x
2
3
3х2 2х 3 1
при х=1-входит в ОДЗ.
12 1
log2
log2 2 1
1
Решение системы, а значит и
неравенства: х=1.
Ответ:
х=1
14.
Решить неравенство7
- x-3
Решение:
log2 (6x x2 7) 1
ОДЗ:
6x x 2 7
˃0
Преобразуем неравенство, умножив левую и правую части на
7
x 3
Т.к. 7
x 3
˃ 0 ,то
log2 (6x x2 7) 7
7
- x-3
7
x-3
log2 (6x x2 7) 7
x 3
Оценим левую часть неравенства:
x 3
2
6x x 2 7 - x 2 6x 7 (x2 6x 9) 2 (x 3) 2 2
log2 ( (x 3)2 2) log2 2,
log2 ( (x 3)2 2) 1.
Оценим правую часть неравенства:
х - 3 0.
7
x 3
70
7
x 3
1
15.
C одной стороныс другой стороны
log2 ( (x 3)2 2) 1,
7
x 3
1
Неравенство log2 (6x x2 7) 7 x 3 имеет решение, если
log 2 (6x x 2 7) 1,
x 3
Решим второе уравнение системы
7
1.
7
x 3
1
7
x 3
7
0
Если х 3, то
х - 3 0. х 3-входит в ОДЗ. 6 3 32 7 ˃ 0
log 2 (6 3 32 7) log 2 2 1
Ответ:
х=3
16.
Найти все значения параметра а, при каждом изкоторых система имеет единственное решение:
4
а(х 1) у 2 х ,
2
2
х у 4.
Решение:
Заметим, что в силу симметричности корней, если пара
(х;у) является решением системы, то и пара (-х;у) тоже
решение системы. Единственность решения возможно
только, если х=0.
4
а(0 1) у 2 0 , а у 2, а у 2,
2
2
2
0
у
4.
у
4.
у 2.
а 0
а 4
17.
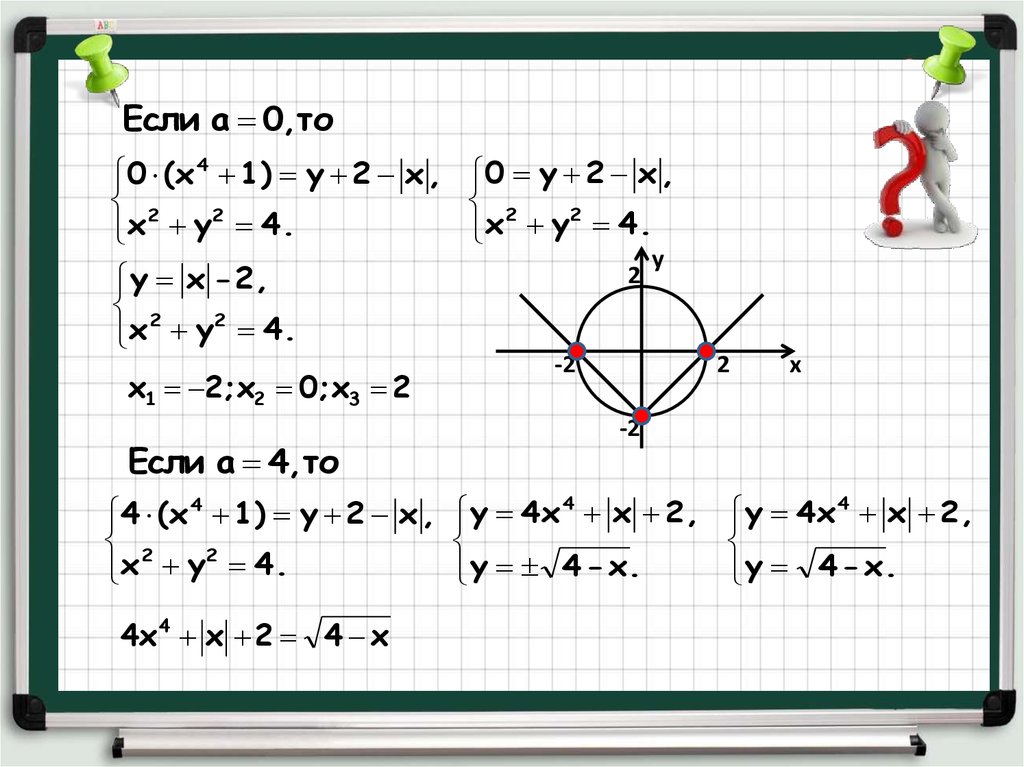
Если а 0,то4
0 (х 1) у 2 х ,
2
2
х у 4.
у х - 2,
2
2
х
у
4.
х1 2;х2 0;х3 2
Если а 4,то
4
4
(х
1) у 2 х ,
2
2
х
у
4.
4х 4 х 2 4 х
0 у 2 х ,
2
2
х у 4.
2
у
-2
2
х
-2
4
у
4х
х 2,
у 4 - х.
4
у
4х
х 2,
у 4 - х.
18.
4х 4 х 2 4 хОценим левую часть уравнения:
4х 4 х 0
4х4 х 2 2
Оценим правую часть уравнения:
-х 0
4-х 4
C одной стороны
с другой стороны
Уравнение
4х 4 х 2 4 х
4х 4 х 2 2
4 х 2
4 х 2
4х 4 х 2 2
4 х 2
имеет решение, если
Решим второе уравнение системы:
4 х 2 х 0
если х 0, то 4 0 4 0 2 2
Ответ:
а=4
19.
Примеры уравнений и неравенств, решаемыхметодом мажорант
1.
x
4
1
4y 4
x
y
2. x 2 2x 2
4
12 x 2 x
2
x 2x 2
3. log 2 (5 cos(3x -
π
2π
)) sin 2 (2x
)
4
3
4. 4 (3x -1)2 log 22 x2 16log4 x 4 12x
5. (x - 3) 4 (x2 2x 3)10 0
6.
- 25x2 20x 12 4 cos 2
15π5
4
20.
Используемые ресурсыШкольная доска
Картинка № 1
Картинка № 2
Картинка № 3
Картинка № 4
Картинка № 5
источник шаблона:
Татарников Виталий Викторович
учитель физики МОУ СОШ №20 п. Баранчинский, г. Кушва, Свердловской обл.
















 mathematics
mathematics








