Similar presentations:
Алгебраическая и тригонометрическая формы записи комплексных чисел
1.
п.23 Алгебраическая итригонометрическая формы
записи комплексных чисел
Выписать основные понятия, определения,
формулы, разобрать задачи. Выполнить задания
№1; №2 слайды 19; 20
2.
ОпределениеКомплексным числом называется
число вида z x yi,
где i 1 , а x и y – вещественные
числа.
2
3.
Основная теорема алгебрыВыражение
z x iy
называется алгебраической формой
записи комплексного числа.
4.
Число x называется действительной частью,y–мнимой частью комплексного числа z.
Это записывают следующим образом:
x Rez,
y Im z.
5.
Если x 0 , то числочисто мнимым.
z называют
Если y 0, то получается z x 0 i
вещественное число.
Два комплексных числа
z x iy
и
z x iy
называются сопряженными.
6.
Два комплексных числа z1 x1 iy1 иz2 x2 iy2 равны друг другу, если
x1 x2 и y1 y2
Комплексное число z считается
равным нулю, если x=y=0.
7.
Всякоекомплексное
число можно
изобразить точкой на плоскости, т.к.
каждому z соответствует упорядоченная
пара вещественных чисел (x;y).
8.
Число z=0 ставится в соответствиеначалу координатной плоскости. Такую
плоскость мы в дальнейшем будем
называть комплексной плоскостью, ось
абсцисс–действительной, а ось ординат–
мнимой осью комплексной плоскости.
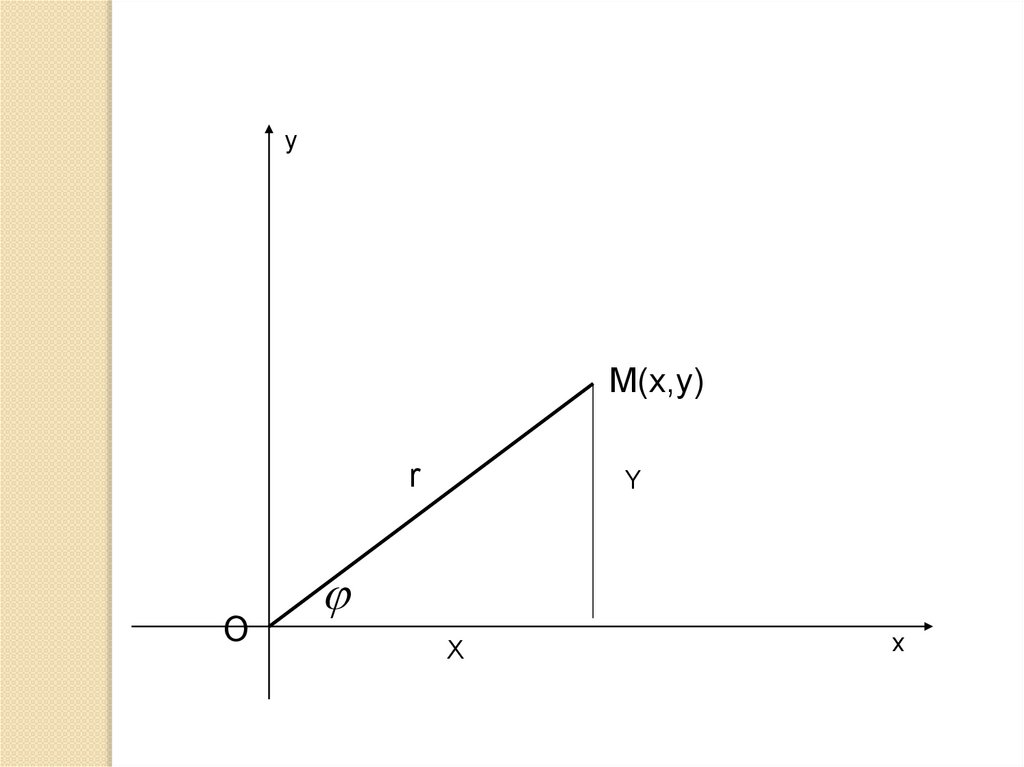
9.
уM(x,y)
r
O
Y
X
х
10.
Модуль комплексного числаЧисло x 2 y 2 называется модулем
комплексного числа z x iy
и
обозначается z .
11.
Тригонометрическая форма записикомплексного числа
Для определения положения точки на
плоскости можно пользоваться полярными
координатами ,
где r–расстояние точки от начала координат,
а φ–угол, который составляет радиус–вектор
этой точки с положительным
направлением оси Ox.
12.
,Положительным направлением
изменения угла φ считается
направление против часовой стрелки.
Воспользовавшись связью декартовых
и полярных координат:
x r cos , y r sin ,
получим тригонометрическую форму
записи комплексного числа
13.
z r cos i sinr x , y
2
,
2
φ – аргумент комплексного числа,
который находят из формул
x
cos
r
y
sin
r
или в силу того, что ,
y
tg
x
y
arctg
x
14.
При переходе от алгебраической формы комплексного числа ктригонометрической
достаточно определить лишь главное значение
аргумента комплексного числа, т.е. считать φ=arg z.
y
Так как arg z , то из формулы tg
получаем, что
x
y
- для внутренних точек I, IV четвертей;
arg z arctg
x
y
arg z arctg - для внутренних точек II четверти;
x
y
arg z arctg - для внутренних точек III четверти.
x
Пример 1. Представить комплексные числа
тригонометрической форме.
z1 1 i
и z2
1
3
в
i
2
2
15.
Решение.Комплексное число z=x+iy в тригонометрической форме
y
r x y , arctg .
x
1) z1=1+i (число z1 принадлежит I четверти), x=1, y=1.
1
2
2
arctg
arctg
1
.
r 1 1 2,
1
4
Таким образом, z1 2 cos i sin .
4
4
1
3
1
3
2) z 2
i (число z2 принадлежит II четверти) x , y
.
2
2
2
2
имеет вид z=r(cosφ +isinφ), где
2
1 3
r
1,
2 2
2
2
2
arctg 3 .
Так как z2 II ч., то Arg z 2
3
3
2
.
3
2
2
i sin
Следовательно, z 2 cos
.
3
3
2
2
i sin
.
Ответ: z1 2 cos i sin , z 2 cos
4
4
3
3
16.
1) Записать число z 2 2 3 iтригонометрической форме:
r z
2
2
2 3
2
2 3
-2
0
4 12 16 4
a 2
1
cos
2
r
4
2
3
b 2 3
3
sin
r
4
2
у
в
х
2
2
z 2 2 3 i 4 cos
i sin
3
3
17.
2525
z 2 cos
i sin
3
3
2) Записать число
в алгебраической форме:
25 24
8 2 4
3
3
3
3
3
z 2 cos 2 4 i sin 2 4 2 cos i sin
3
3
3
3
1
3
1 i 3
2 i
2
2
18.
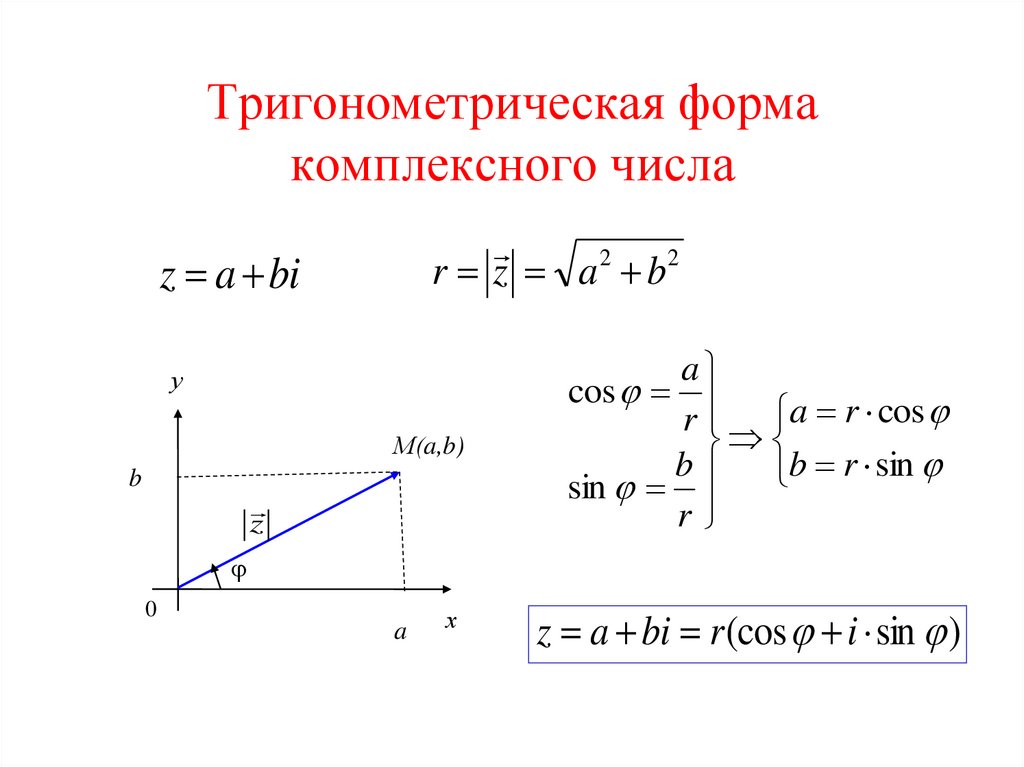
Тригонометрическая формакомплексного числа
2
2
r z a b
z a bi
у
М(a,b)
b
z
a
cos
r a r cos
b b r sin
sin
r
0
a
х
z a bi r (cos i sin )
19.
Выполнить №1 и №2№1 Записать в тригонометрической форме
комплексное число
z 1 i 3
.
.
20.
z 2 cos i sin6
6
№2 Записать число
в алгебраической форме:


















 mathematics
mathematics








