Обратная функция

1.

Обратная функция
https://www.youtube.com/watch?v=lffsY8VYv7U

2.

3. Задание

Найдите функцию, обратную данной:
y 5x 2
3
y
x 1
постройте графики этих функций

4. СЛОЖНАЯ ФУНКЦИЯ

Сложная – не значит трудная!

5. Повторение.

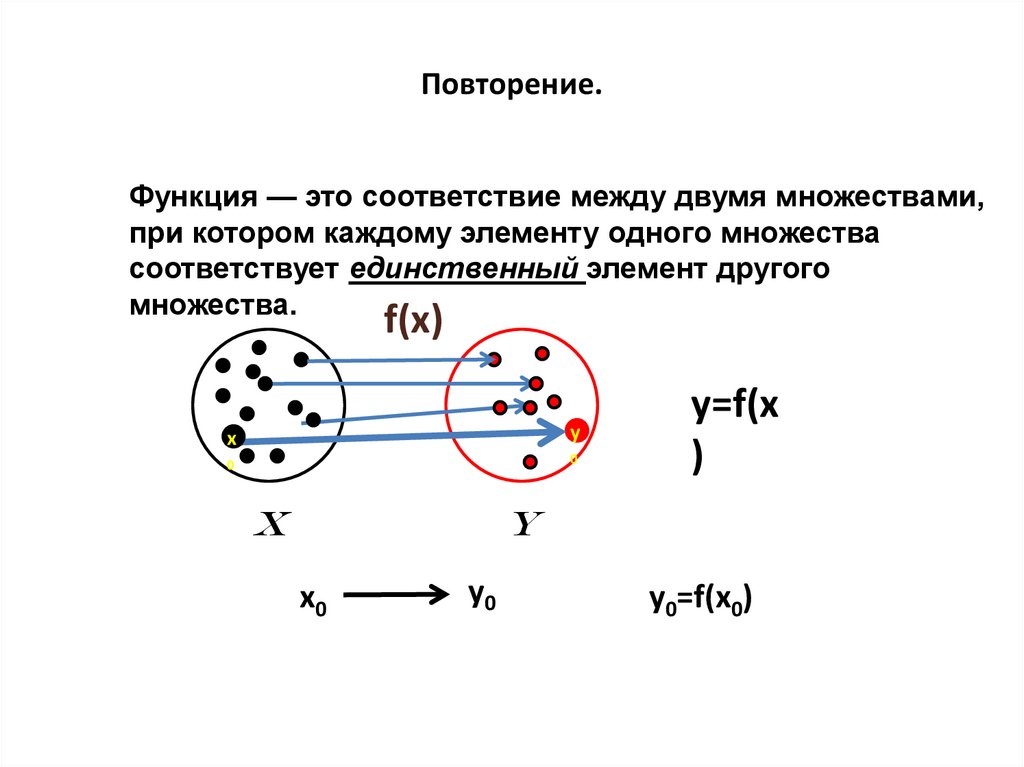
Функция — это соответствие между двумя множествами,
при котором каждому элементу одного множества
соответствует единственный элемент другого
множества.
f(x)
x
у
0
0
X
y=f(x
)
Y
x0
y0
y0=f(x0)

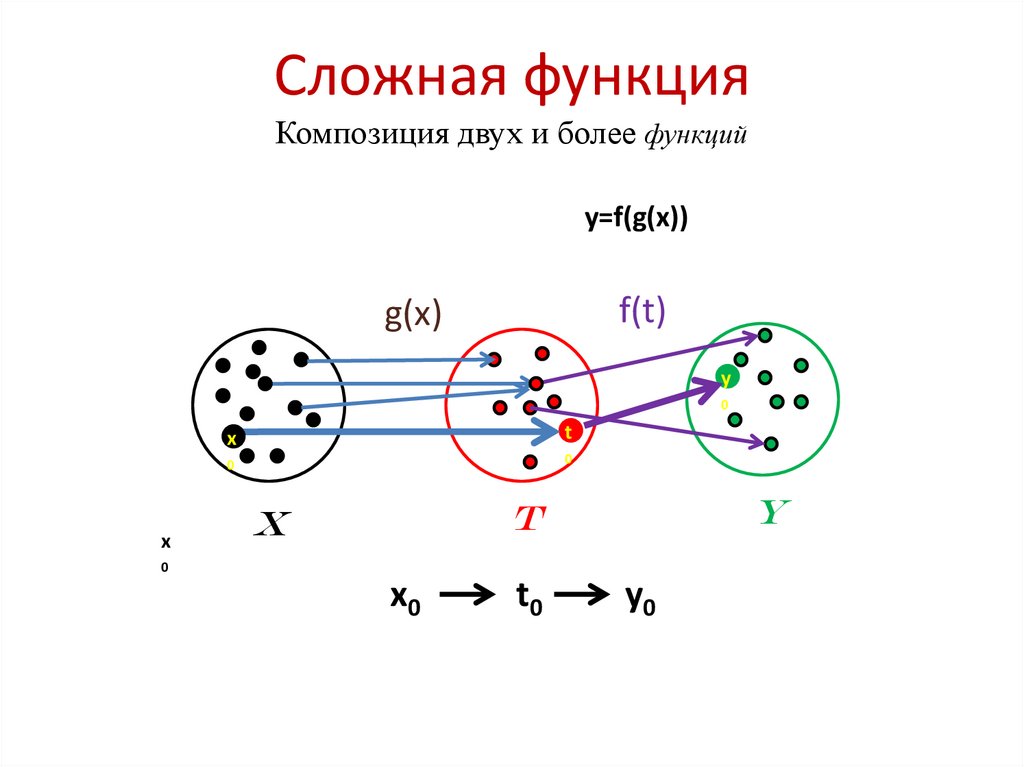
6. Сложная функция Композиция двух и более функций

y=f(g(x))
f(t)
g(x)
у
0
x
x
t
0
0
Y
T
X
0
x0
t0
y0

7.

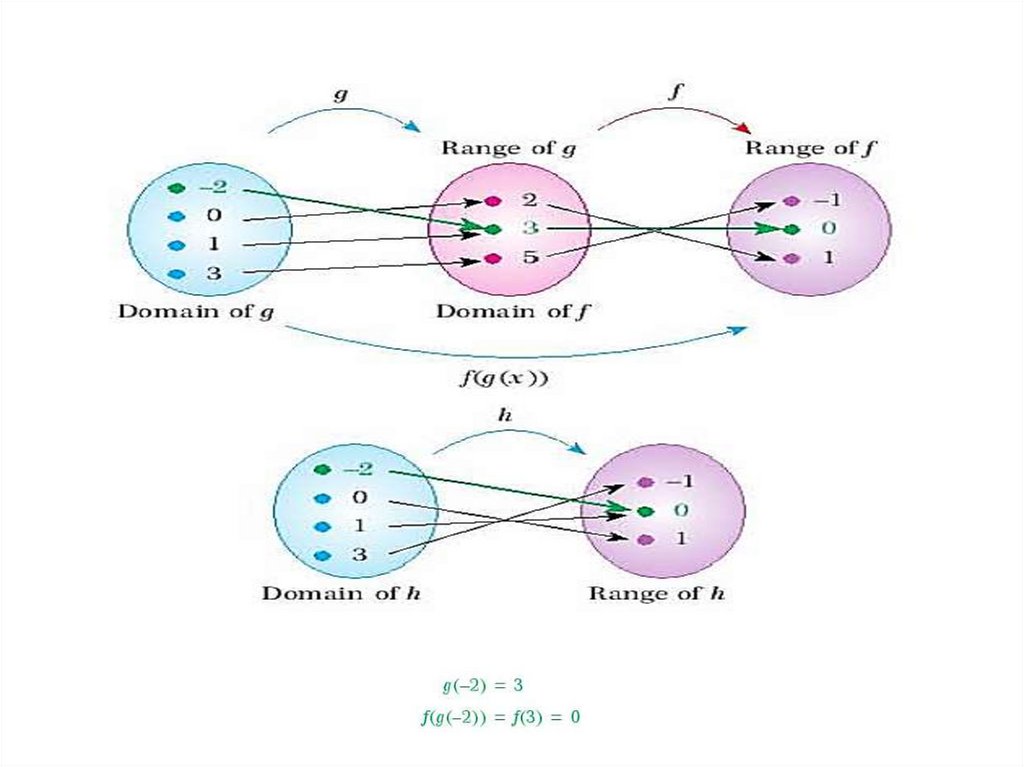
8. Определение: Функции, у которых аргумент в свою очередь также является функцией, называются сложной функций или композицией

функций.
Сложная
функция – функция от функции.

9. Формула для задания сложной функции

Пример.
y=f(g(x)) –
– сложная функция
у х 4
2
g(x) – внутренняя функция
g(x) = х2 - 4 –
внутренняя функция
f(t) – внешняя функция
f(t) = t – внешняя
функция

10. Примеры сложной функции y=f(g(x))

внешняя
функция
f(t)
внутренняя
функция
g(x)
1. y = sin2x
1. sin t
2. y = (x3 – 1 )5
2. t5
x3-1
3.
3. cos t
7x+2
4.
y = cos(7x + 2)
y=
1
x2 x
5. y = sin2x + sin x
4.
1
t
5. t2+t
2x
x2-x
sin x

11. Составьте сложную функцию ,если f(x)=x2, g(x)=2x-4, h(x)=sin x например: y=h(f(x))=sin x2

• y1=f(g(x))
• y2=g(f(x))
• y3= f(h(x))
• y4=h(g(x))

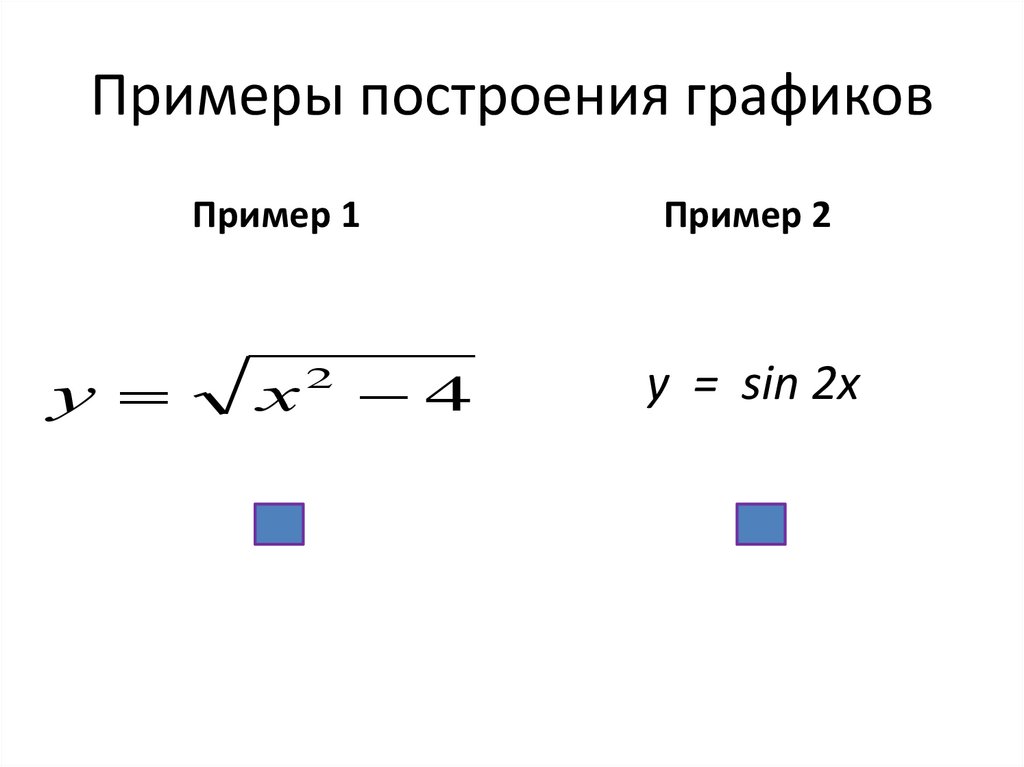
12. Примеры построения графиков

Пример 1
у
х
2
4
Пример 2
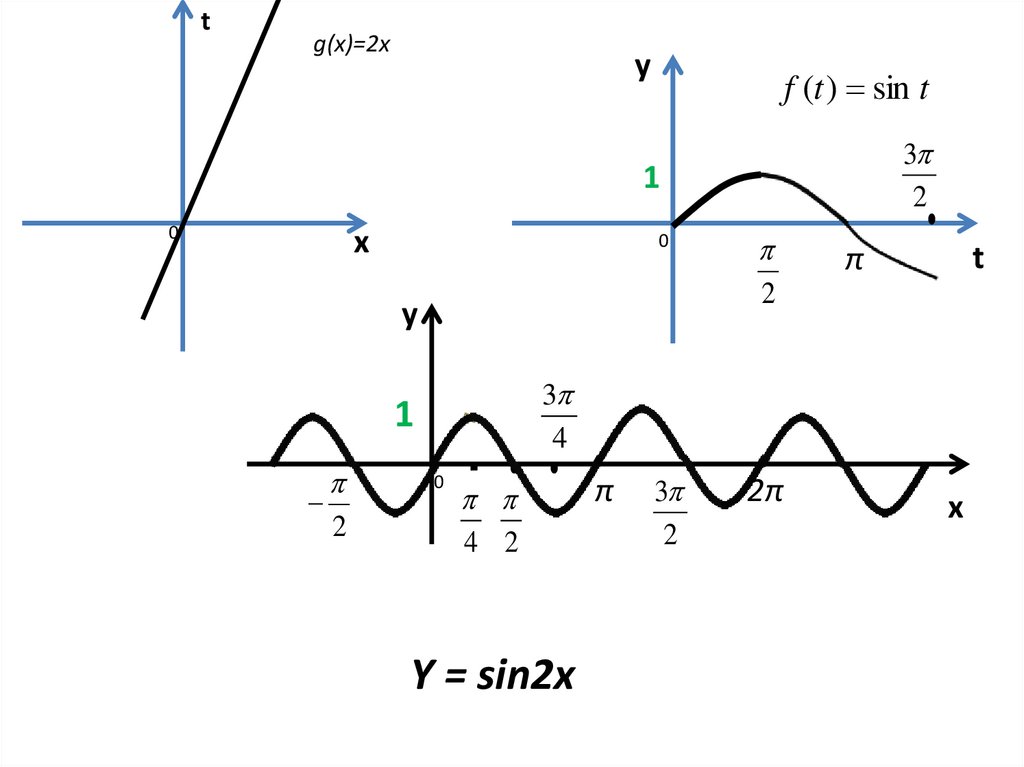
y = sin 2x

13. Пример 1

у х2 4
1. Найдем область определения функции:
D(y) = (-∞; -2] U [2; +∞)
Функция четная.
2. Построим графики
внутренней и внешней функции:
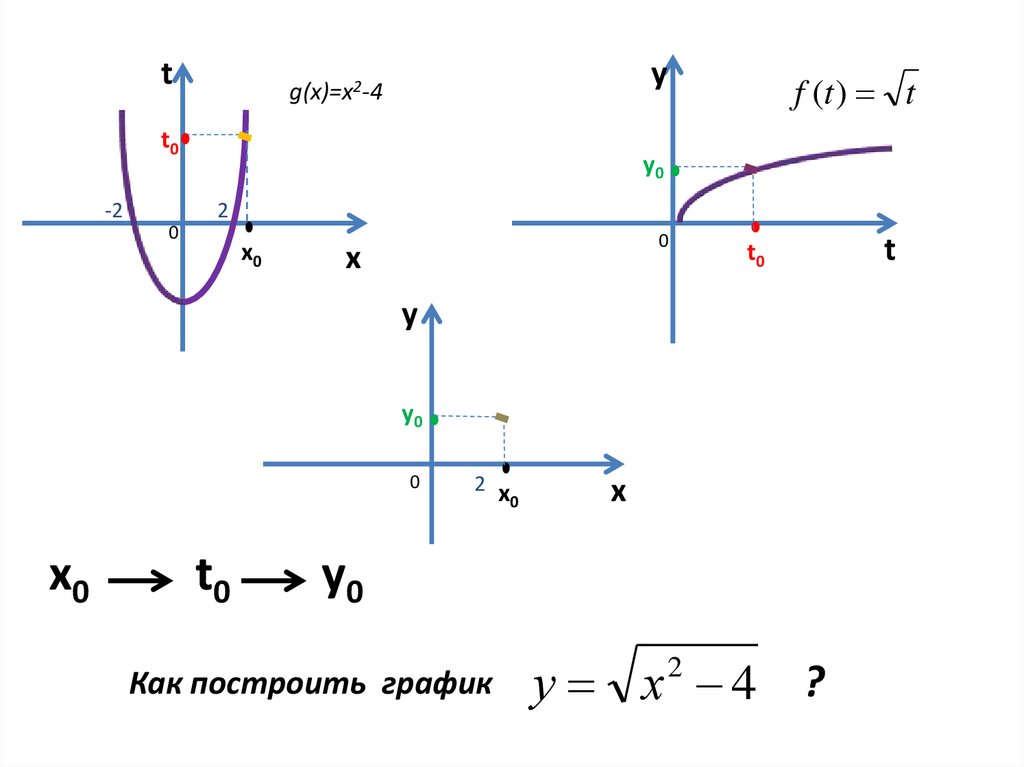
g(x)=x2-4
f (t ) t

14.

t
y
g(x)=x2-4
t0
-2
f (t ) t
y0
2
0
x0
0
х
t0
y
y0
0
x0
t0
2 x
0
х
y0
Как построить график
у х 4 ?
2
t

15.

t
y
g(x)=x2-4
t0
-2
f (t ) t
y0
2
0
x0
0
х
t0
t
y
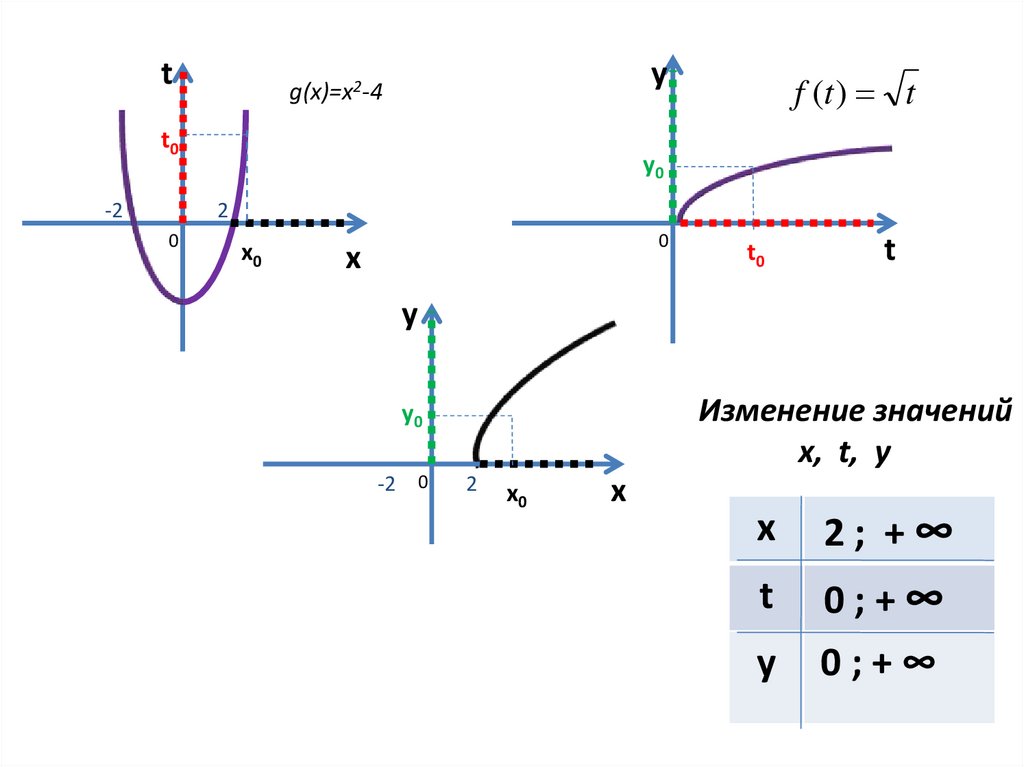
Изменение значений
x, t, y
y0
-2 0
2
x0
х
х
2; +∞
t
0;+∞
y
0;+∞

16.

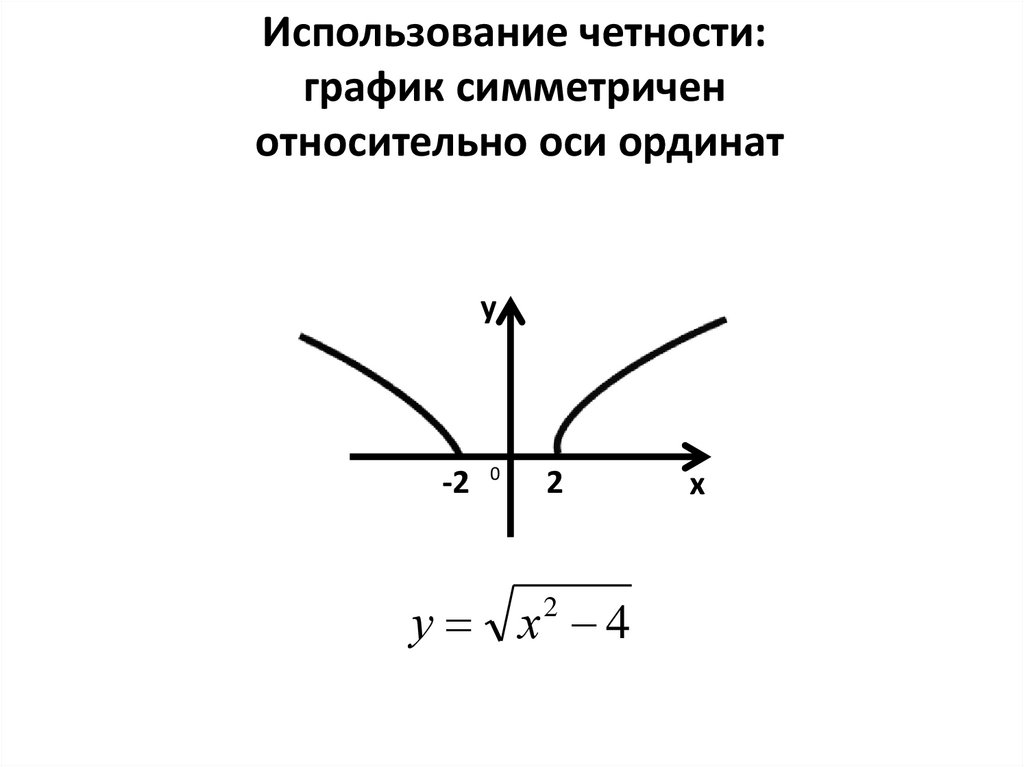
Использование четности:
график симметричен
относительно оси ординат
y
-2
0
2
у х 4
2
х

17. Пример 2

у sin 2 x
1. D(y) = R
Функция нечетная.
Функция периодическая, период: π.
2. Построим графики
внутренней и внешней функции:
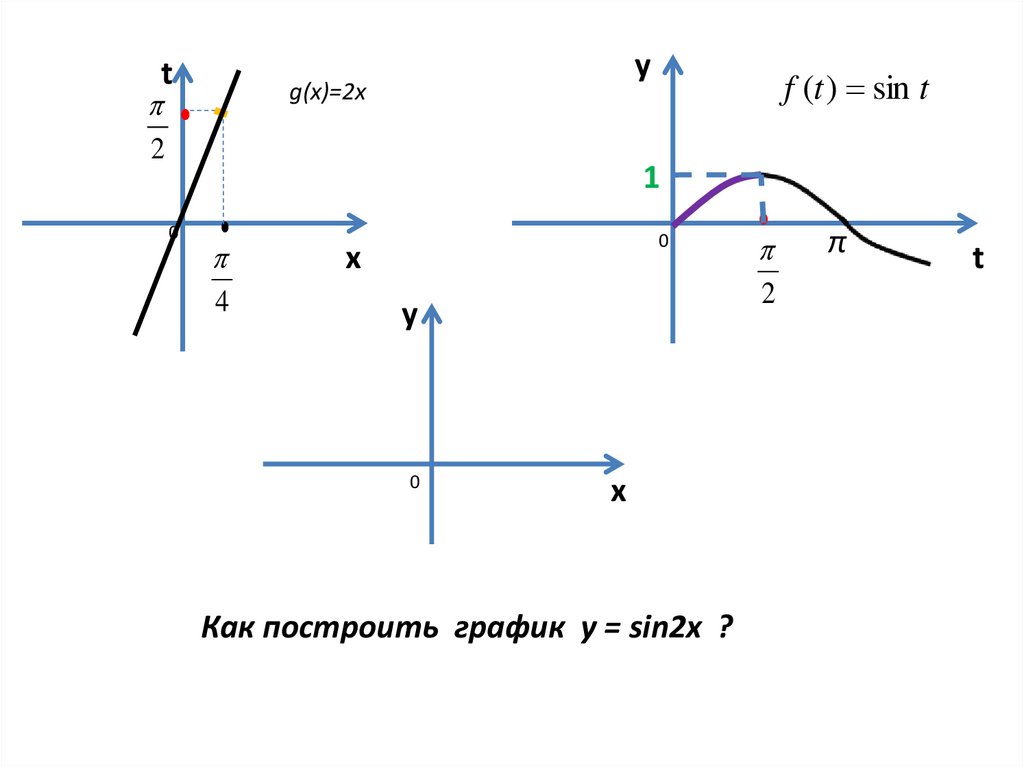
g(x)=2х
f (t ) sin t

18.

t
y
g(x)=2x
2
f (t ) sin t
1
0
4
0
х
y
0
х
Как построить график y = sin2x ?
2
π
t

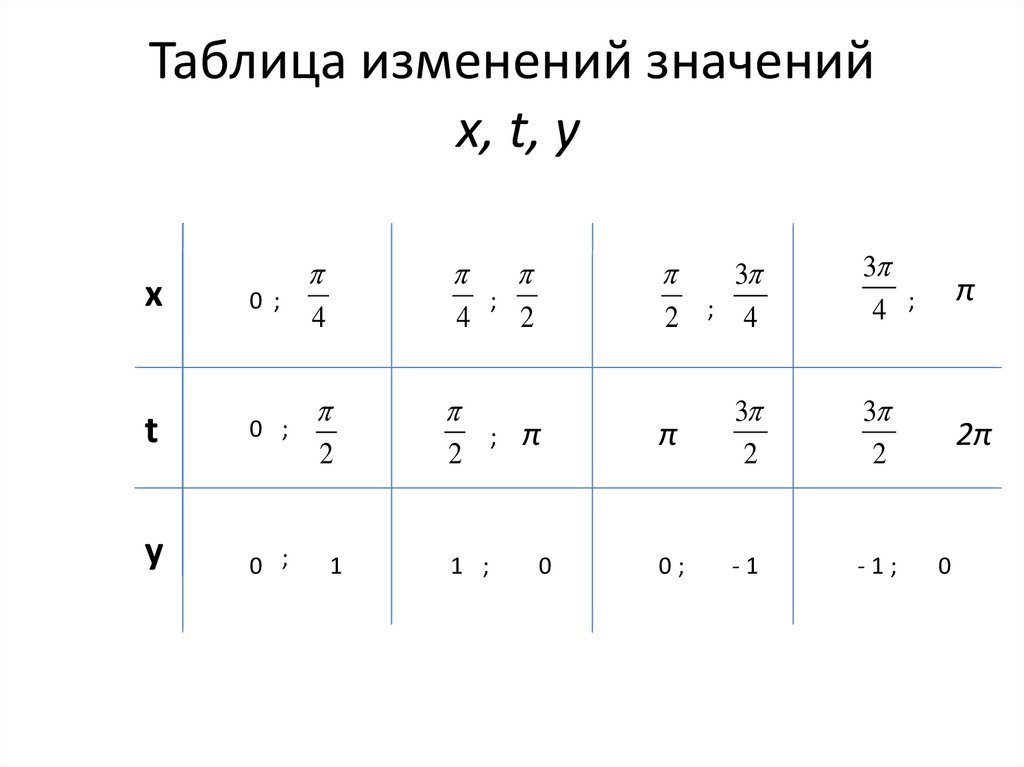
19. Таблица изменений значений x, t, y

x
t
y
0 ;
4
;
4
2
3
2 ; 4
3
;
4
π

20.

tt
y
g(x)=2x
2
f (t ) sin t
1
0
4
х
y
t
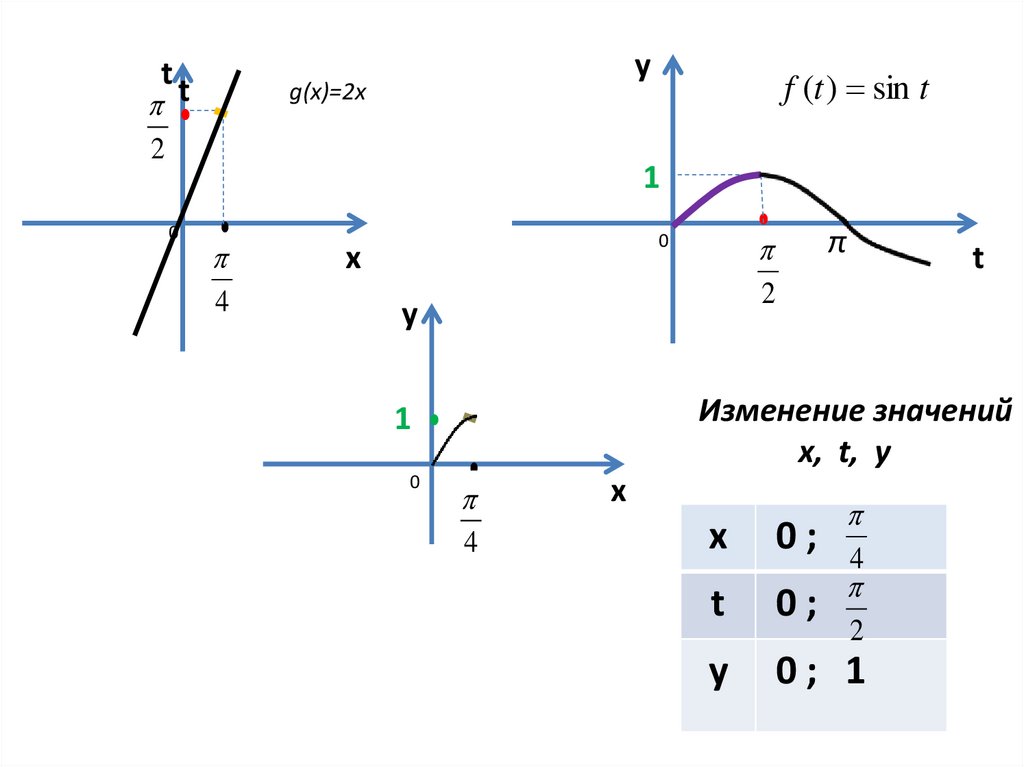
Изменение значений
x, t, y
1
0
π
2
0
4
х
4
2
х
0;
t
0;
y
0; 1

21.

π
t
g(x)=2x
y
2
f (t ) sin t
1
0
4 2
х
2
0
y
t
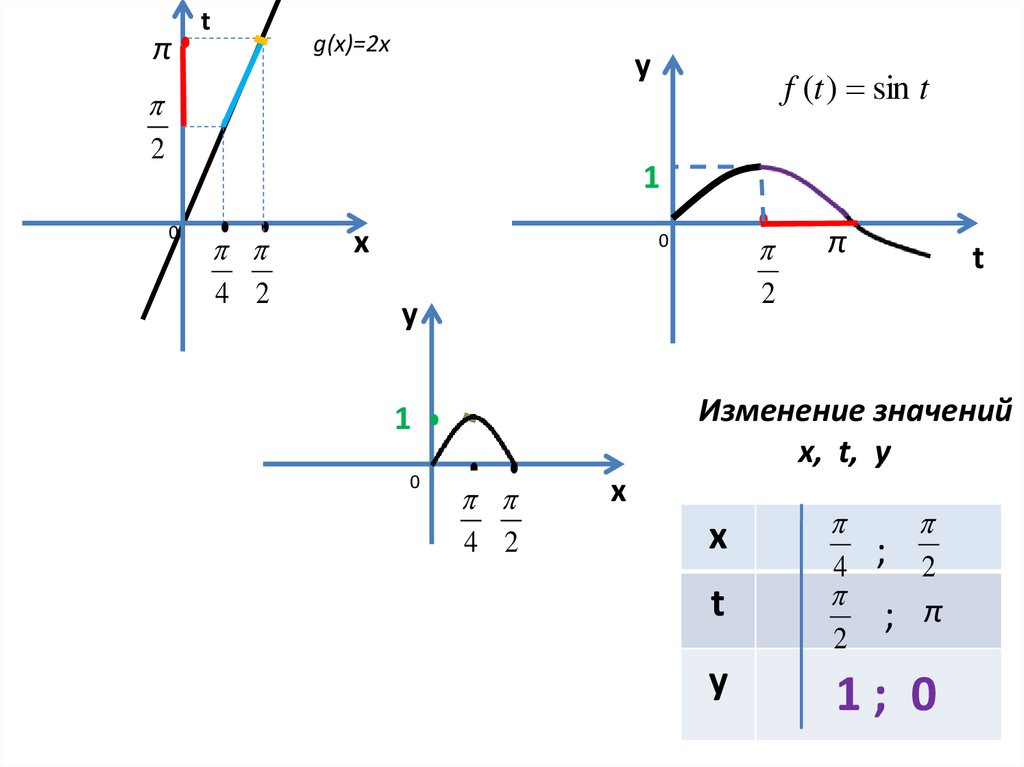
Изменение значений
x, t, y
1
0
π
4 2
х
х
t
y
4
2
;
2
; π
1; 0

22.

π
t
g(x)=2x
y
f (t ) sin t
3
2
1
0
3
2 4
х
y
3
2
1
0
4 2
π
2
0
t
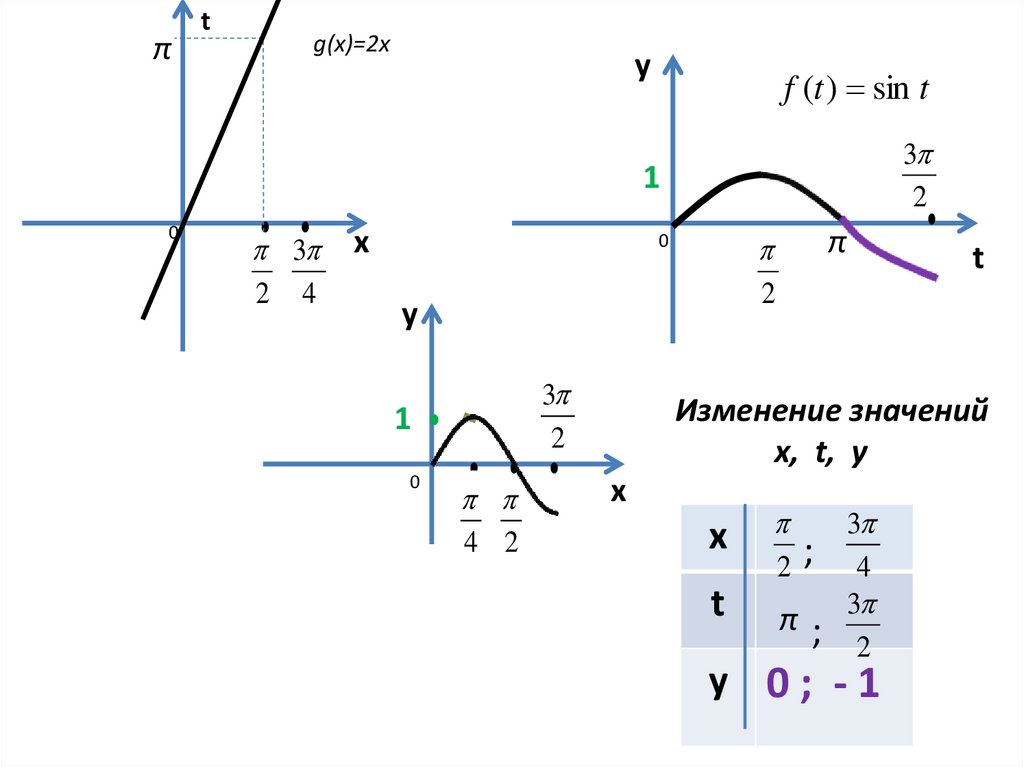
Изменение значений
x, t, y
х
х
t
2
;
π;
3
4
3
2
y 0; -1

23.

π
t
g(x)=2x
y
f (t ) sin t
3
2
1
0
3
2 4
х
2
0
y
3
2
1
0
4 2
2π х
2π
π
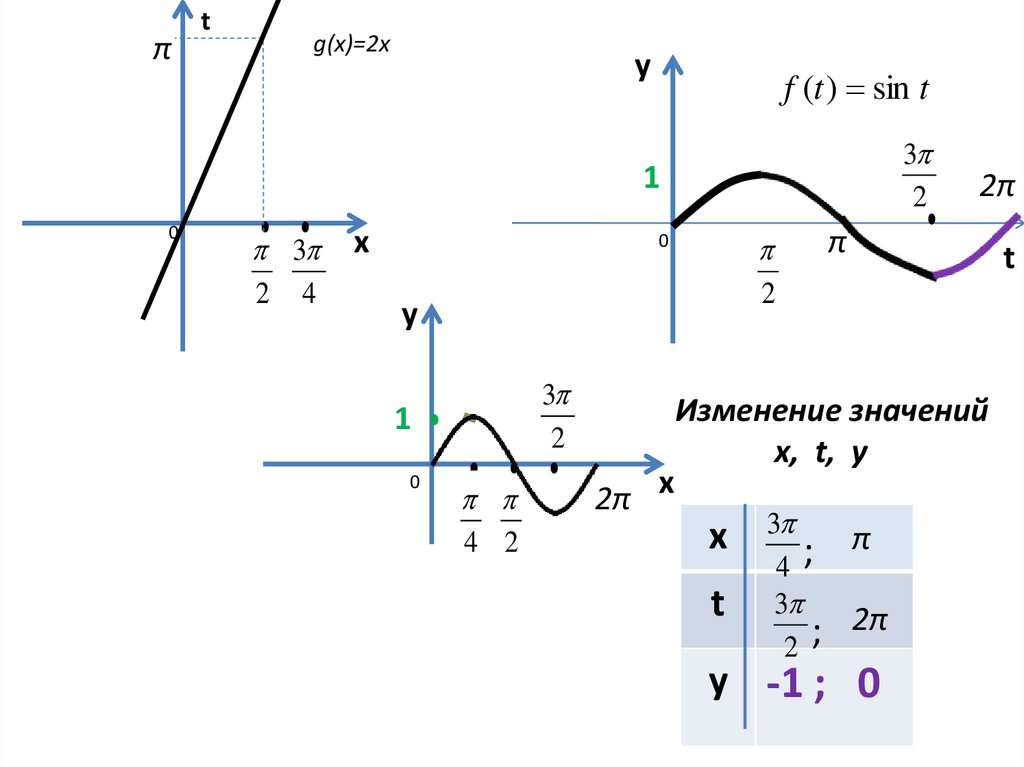
Изменение значений
x, t, y
х
t
3
π
;
4
3
2π
;
2
y -1 ; 0
t

24. Таблица изменений значений x, t, y

3
4 ;
π
π
3
2
3
2
2π
0;
-1
-1;
x
0 ;
4
;
4
2
3
2 ; 4
t
0 ;
2
; π
2
y
0 ;
1 ;
1
0
0

25.

t
g(x)=2x
y
f (t ) sin t
3
2
1
0
х
0
2
3
2
2π
y
3
4
1
2
t
π
0
4 2
Y = sin2x
π
х

26. Нахождение множества значений сложной функции

Пример. Дана функция
y
1
3 sin x
Найдите Е(у).
Решение.
Внутренняя функция принимает значения от 2 до 4, так как 2≤3+sinx≤4.
Рассмотрим внешнюю функцию:
1
f (t )
t
Заметим, что она определена только при тех значениях t, для которых
2≤t≤4.

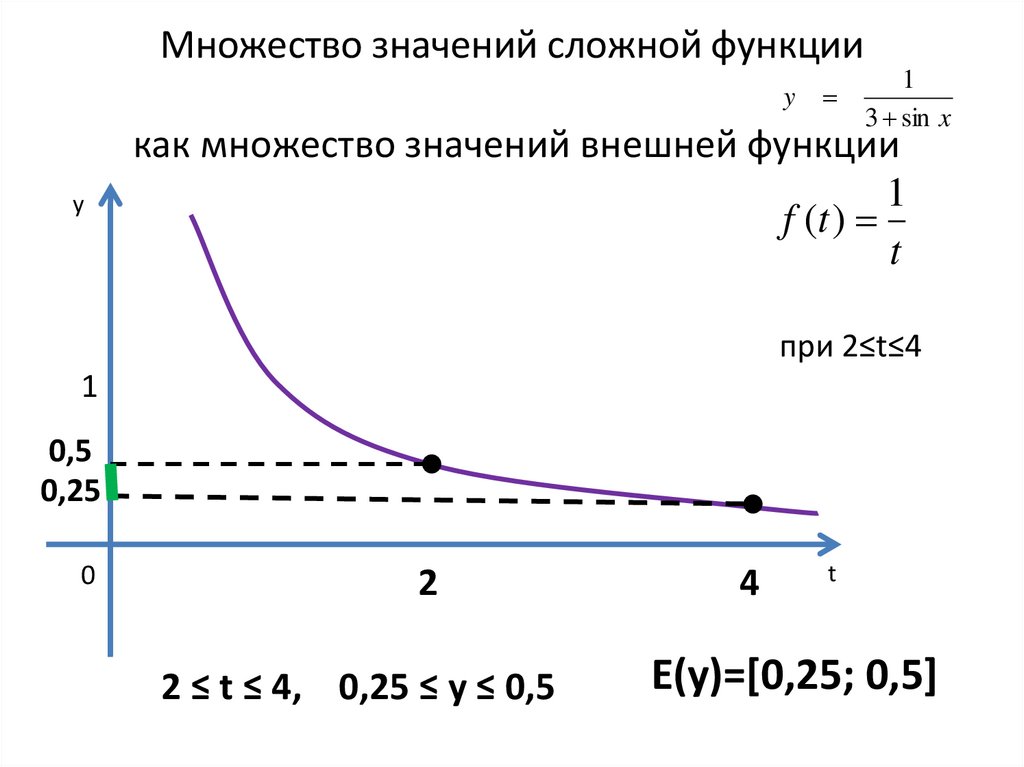
27. Множество значений сложной функции как множество значений внешней функции

Множество значений сложной функции
y
y
1
3 sin x
как множество значений внешней функции
1
f (t )
t
при 2≤t≤4
1
0,5
0,25
0
2
2 ≤ t ≤ 4, 0,25 ≤ y ≤ 0,5
4
t
E(y)=[0,25; 0,5]

28.

РЕФЛЕКСИЯ
Я......................................... ознакомился.
Мне .................................... было нелегко.
Я .................................... усвоил
Я ............................ .......запомнил.