Перпендикулярність площин

1.

Тема уроку:
1

2.

Яким може бути взаємне розміщення
двох площин в просторі?
α
α
α║β
с
β
β
α∩β=с

3.

Означення та ознаку перпендикулярних
прямих.
Означення та ознаку
перпендикулярності прямої і площини.

4.

Означення
перпендикулярних прямих

5.

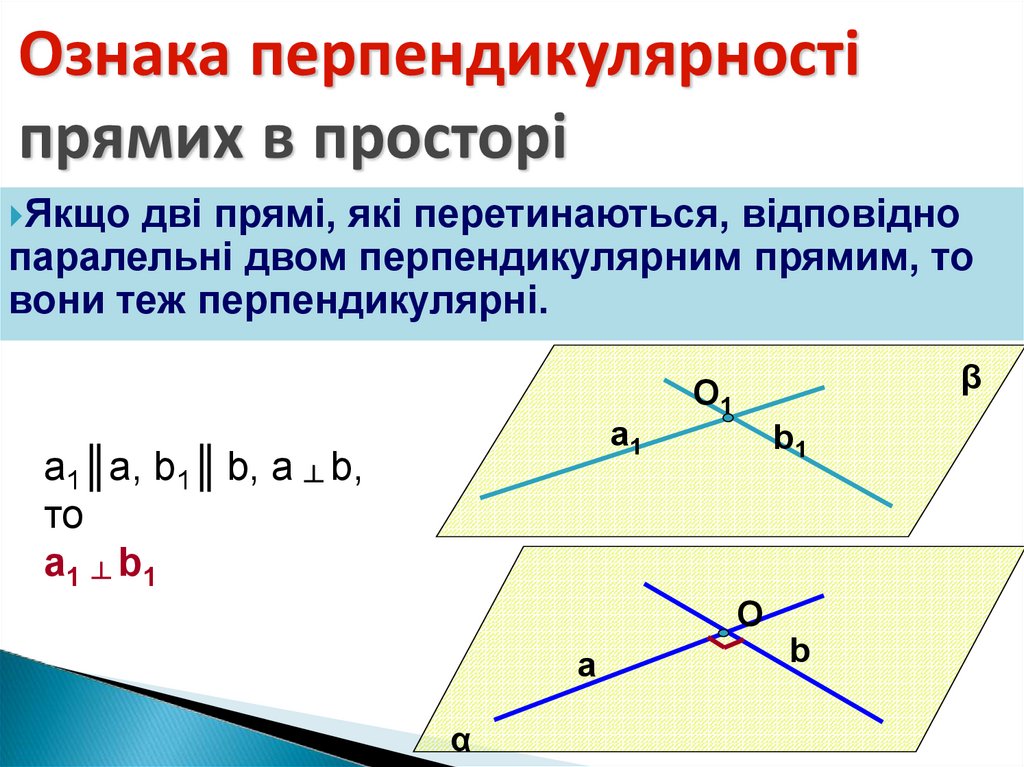
Ознака перпендикулярності
прямих в просторі
Якщо
дві прямі, які перетинаються, відповідно
паралельні двом перпендикулярним прямим, то
вони теж перпендикулярні.
а1
а1║а, b1║ b, а ┴ b,
то
а1 ┴ b1
β
О1
b1
O
а
α
b

6.

Означення перпендикулярних
прямої та площини
a
Пряма, яка перетинає
площину, називається
перпендикулярною до цієї
площини, якщо вона
перпендикулярна до
довільної прямої, що лежить
на цій площині і проходить
через їхню точку перетину.
хn
х3
х2
х1
α
О

7.

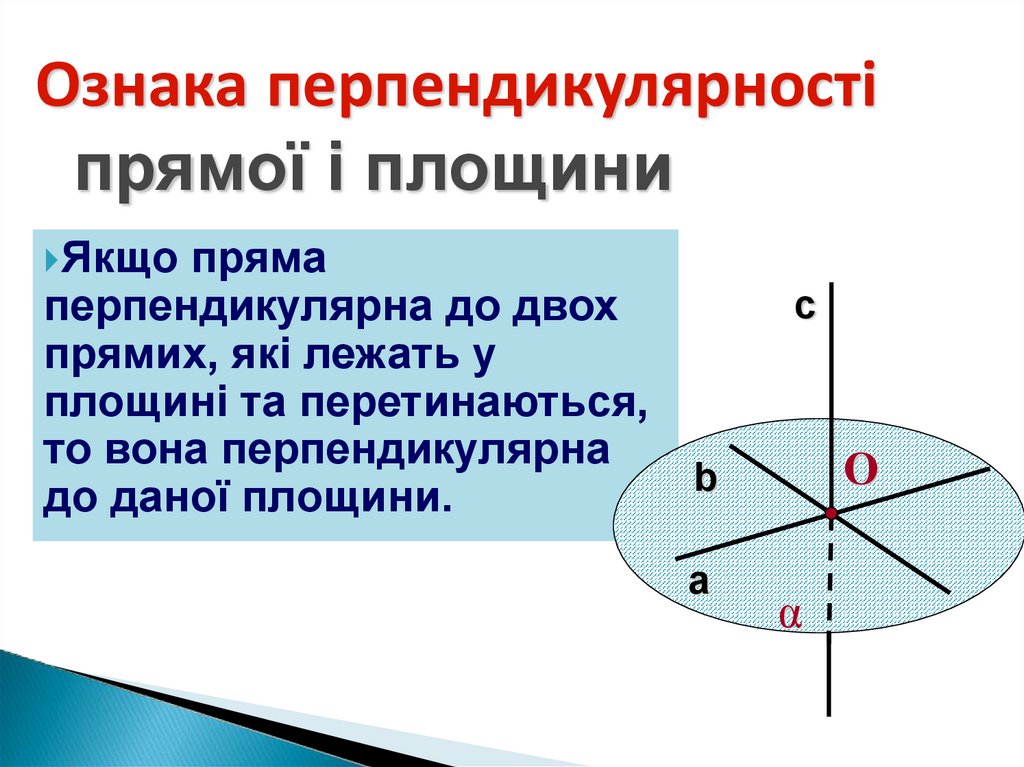
Ознака перпендикулярності
прямої і площини
Якщо
пряма
перпендикулярна до двох
прямих, які лежать у
площині та перетинаються,
то вона перпендикулярна
до даної площини.
с
О
b
a
α

8.

Означення перпендикулярних площин
Дві площини, що перетинаються, називаються
перпендикулярними, якщо третя площина,
перпендикулярна до прямої перетину цих площин,
перетинає їх по перпендикулярних прямих.
Якщо α∩β=с,
∩α=а, ∩β=b,
с ┴ і а ┴ b, то
α ┴β
b
β
с
α
а

9.

Ознака перпендикулярності
площин
Якщо
одна з двох площин проходить
через пряму, перпендикулярну до другої
площини, то ці площини перпендикулярні.
Дано: α, а ┴ α;
а∩α=О; площина β
проходить через а.
Довести: β ┴ α.
β
α
а
О
b

10.

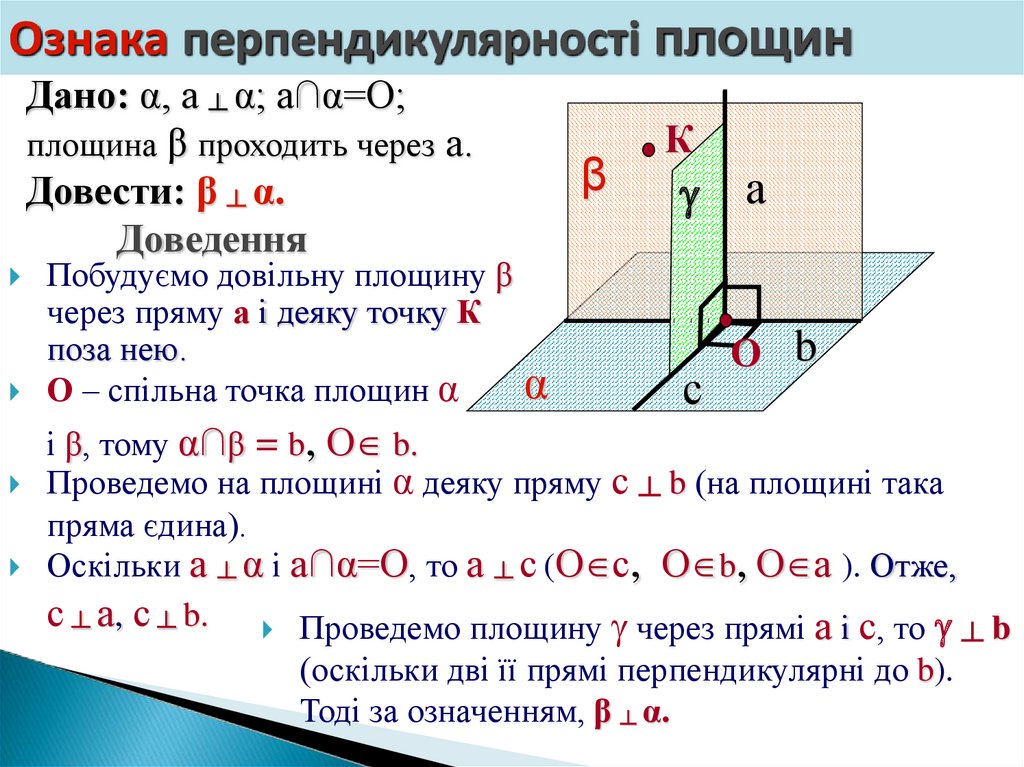
Ознака перпендикулярності площин
Дано: α, а ┴ α; а∩α=О;
площина β проходить через а.
Довести: β ┴ α.
Доведення
Побудуємо довільну площину β
через пряму а і деяку точку К
поза нею.
О – спільна точка площин α
β
α
К
с
а
О b
і β, тому α∩β = b, О b.
Проведемо на площині α деяку пряму с ┴ b (на площині така
пряма єдина).
Оскільки а ┴ α і а∩α=О, то а ┴ с (О с, О b, О а ). Отже,
с ┴ а, с ┴ b. Проведемо площину через прямі а і с, то
(оскільки дві її прямі перпендикулярні до b).
Тоді за означенням, β ┴ α.
┴b