Перпендикулярність площин

1.

Перпендикулярність
площин

2. Перпендикулярність двох площин

ПЕРПЕНДИКУЛЯРНІСТЬ ДВОХ ПЛОЩИН
Перпендикулярні площини – дві площини що
перетинаються, для яких виконується умова, що
третя площина, перпендикулярна лінії їх
перетину, перетинає їх по перпендикулярним
прямим.
Площини α і β перпендикулярні
(α ⊥ β), якщо площина Υ ⊥ c,
Υ перетинає α і β по
взаємноперпендикулярним
прямим a і b,
(a ⊥ b).

3. ОЗНАКА ПерпендикулярнОСТІ площин

ОЗНАКА ПЕРПЕНДИКУЛЯРНОСТІ ПЛОЩИН
Якщо пряма, що належить
одній площині,
перпендикулярна другої
площині , то ці площини
перпендикулярни
(якщо a ⊂ α, a ⊥ β, то α ⊥ β).

4.

ВЛАСТИВОСТІ ПЕРПЕНДИКУЛЯРНИХ ПЛОЩИН
1. Будь-яка площина , перпендикулярна
прямої перетину перпендикулярних
площин, перетинає їх по
перпендикулярним прямим.
(якщо α ∩ β = c, α ⊥ β, α ∩ Υ = a,
γ ∩ β = b і γ ⊥ c, то a ⊥ b)
2. Якщо пряма, що належить одной з
двох перпендикулярних площин,
перпендикулярна прямій їх перетину,
то вона перпендикулярна й другій
площині.
(якщо α ⊥ β, α ∩ β = b, a € α і a ⊥b,
то a ⊥ β)

5.

ВЛАСТИВОСТІ ПЕРПЕНДИКУЛЯРНИХ ПЛОЩИН
3. Через будь-яку точку простору
можна провести площину,
перпендикулярну даної
площині.
4 Дві площини, перпендикулярні третій площині, або
паралельні, або перетинаються
по прямій, перпендикулярній
третій площині.

6.

ВЛАСТИВОСТІ ПЕРПЕНДИКУЛЯРНИХ ПЛОЩИН
5. Три попарно перпендикулярні
площини перетинаються по
трьом перпендикулярним
прямим
(якщо α ⊥ β, β ⊥ Υ, Υ ⊥ α, то
a ⊥ b, b ⊥ c, a ⊥ c)
6 .Через дану пряму деякої площини
можно провести площину,
перпендикулярну даній площині.

7.

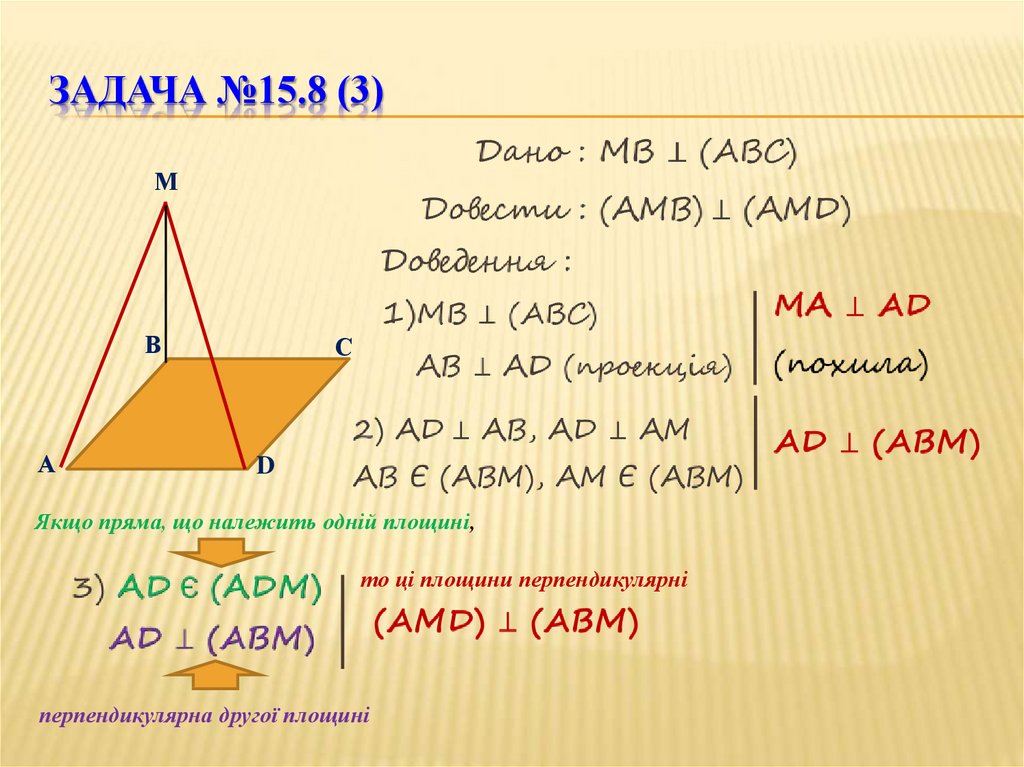
ЗАДАЧА №15.8 (3)
М
В
А
С
D
Якщо пряма, що належить одній площині,
то ці площини перпендикулярні
перпендикулярна другої площині

8.

ДЛЯ РОЗВ’ЯЗУВАННЯ ЗАДАЧ
Перпендикулярні площини зображують :
α
β
α
β