Паралельність площин

1.

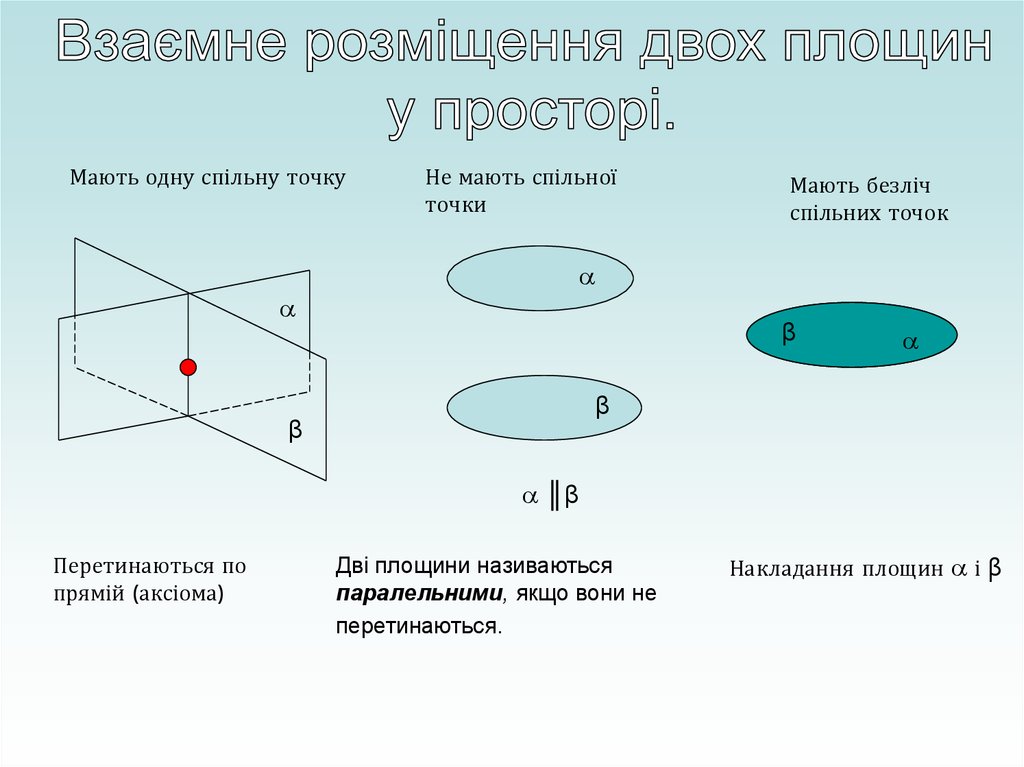
Мають одну спільну точку
Не мають спільної
точки
Мають безліч
спільних точок
β
β
β
║β
Перетинаються по
прямій (аксіома)
Дві площини називаються
паралельними, якщо вони не
перетинаються.
Накладання площин і β

2.

• Виконання вправ
• 1. Наведіть приклади паралельних
площин із оточення.

3.

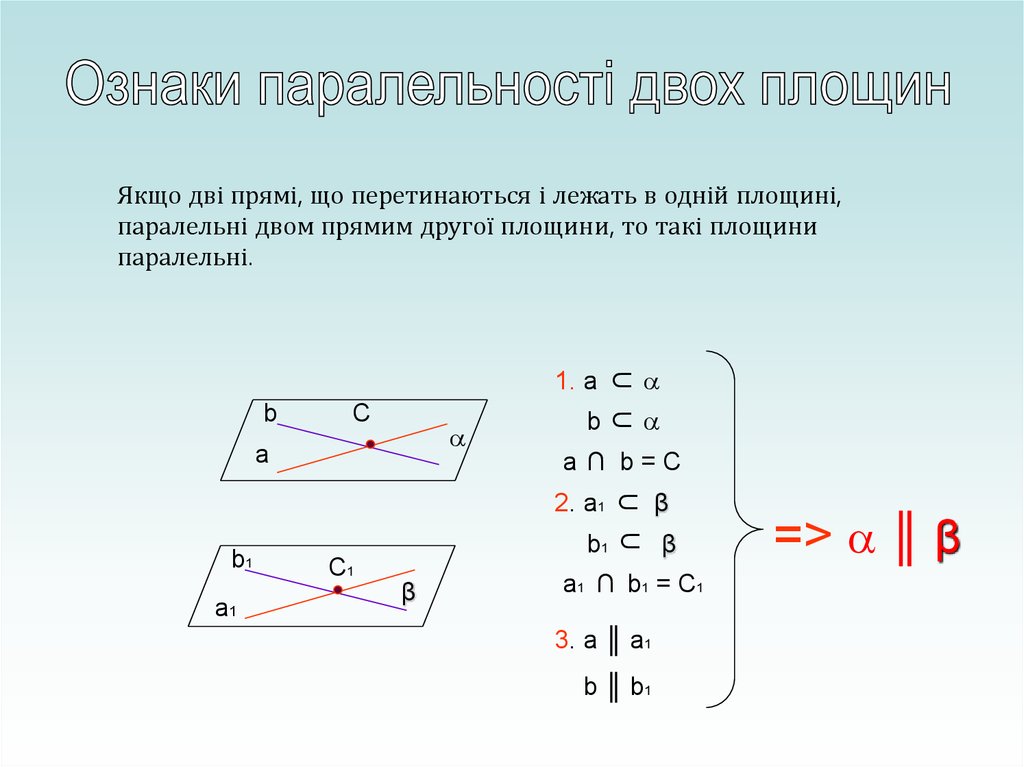
1. a
C
a
b
a1
C1
b1
β
a ∩ b=C
2. a1
b1
∩ ∩
b
∩ ∩
Якщо дві прямі, що перетинаються і лежать в одній площині,
паралельні двом прямим другої площини, то такі площини
паралельні.
β
β
a1 ∩ b1 = C1
3. a ║ а1
b ║ b1
=> ║ β

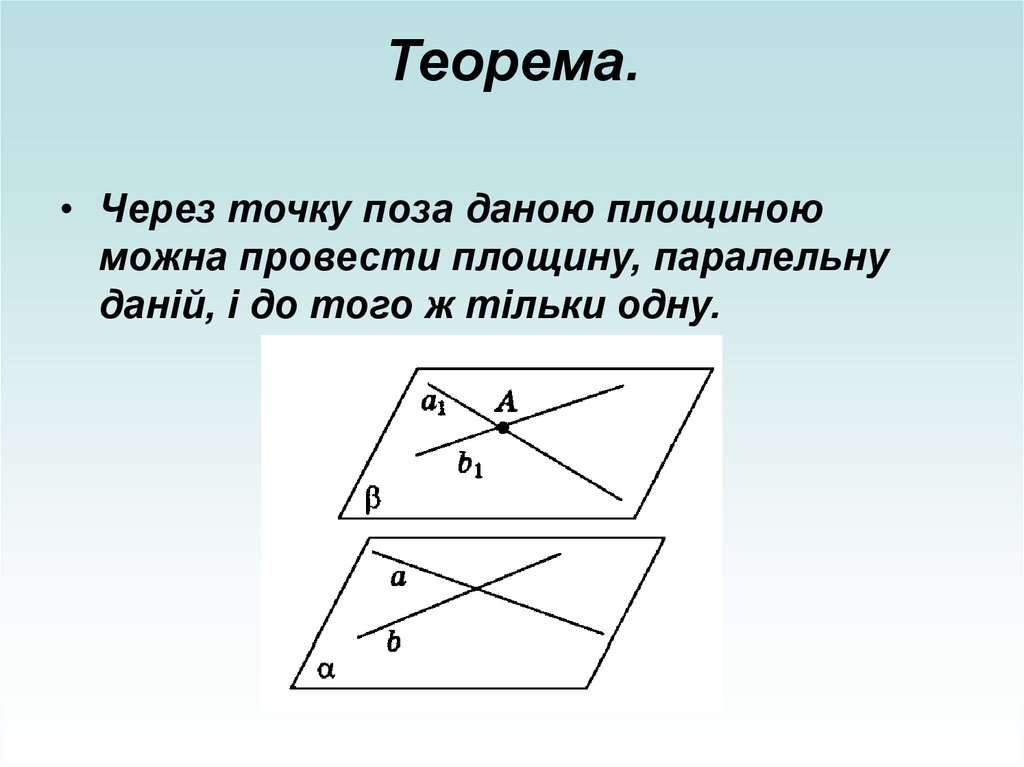
4. Теорема.

• Через точку поза даною площиною
можна провести площину, паралельну
даній, і до того ж тільки одну.

5.

• Виконання вправ
• Через пряму а, яка паралельна площині
, проведіть площину, паралельну даній
площині . Скільки площин можна
провести?

6.

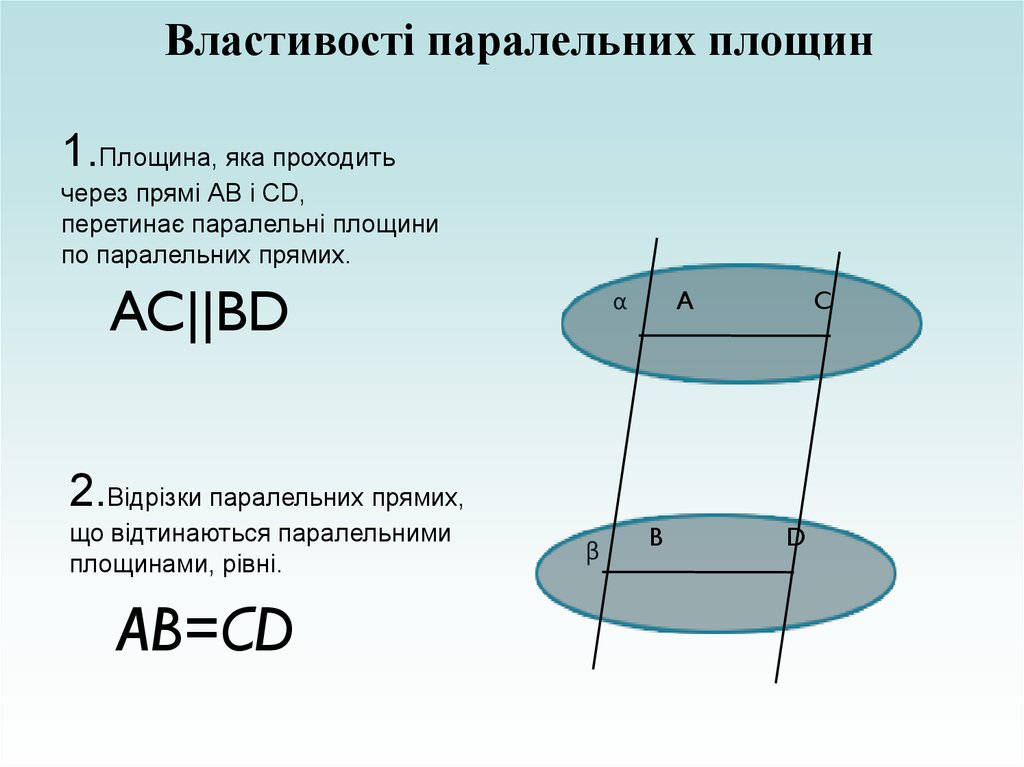
Властивості паралельних площин
1.Площина, яка проходить
через прямі АВ і СD,
перетинає паралельні площини
по паралельних прямих.
AC||BD
A
α
C
2.Відрізки паралельних прямих,
що відтинаються паралельними
площинами, рівні.
AB=CD
β
B
D

7.

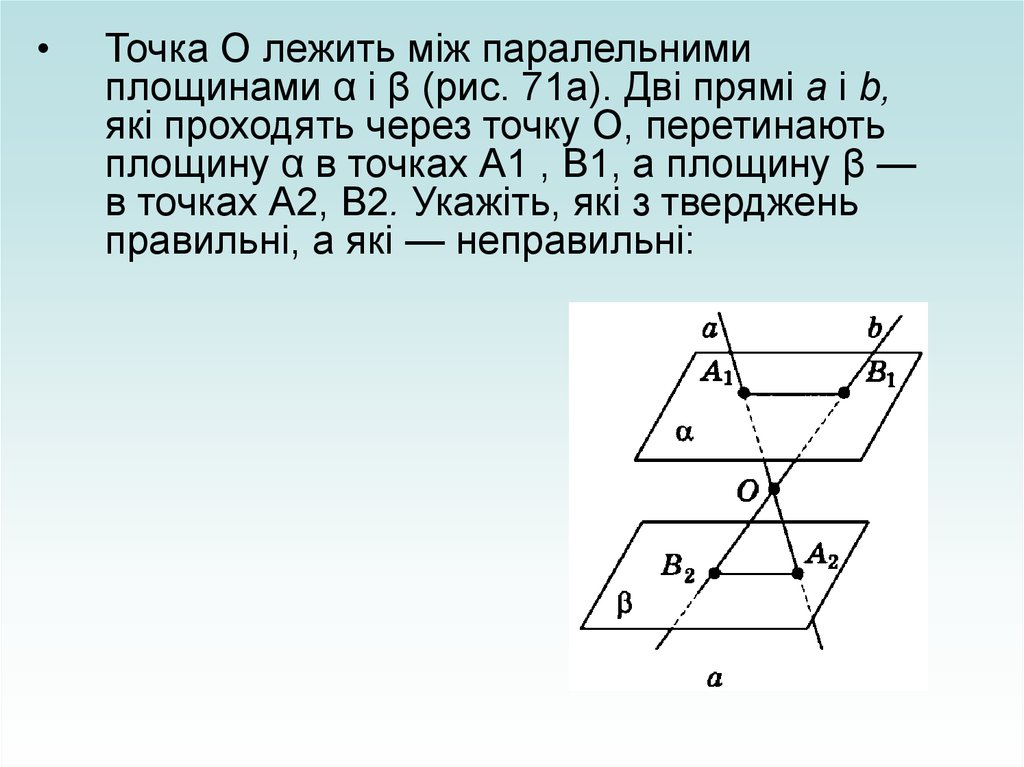
Точка О лежить між паралельними
площинами α і β (рис. 71а). Дві прямі а і b,
які проходять через точку О, перетинають
площину α в точках А1 , B1, а площину β —
в точках А2, В2. Укажіть, які з тверджень
правильні, а які — неправильні:

8.

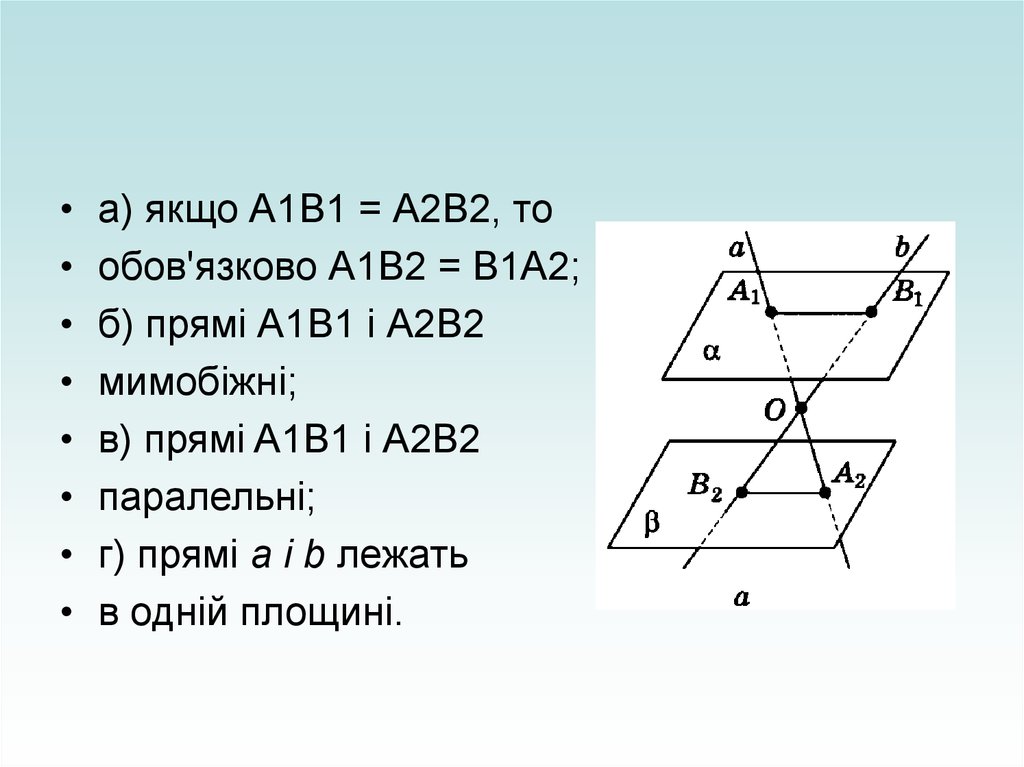
а) якщо А1В1 = А2В2, то
обов'язково А1В2 = В1А2;
б) прямі А1В1 і А2B2
мимобіжні;
в) прямі A1B1 і А2B2
паралельні;
г) прямі а і b лежать
в одній площині.