Взаємне розміщення прямих у просторі

1.

2.

Розміщення прямих у просторі

3.

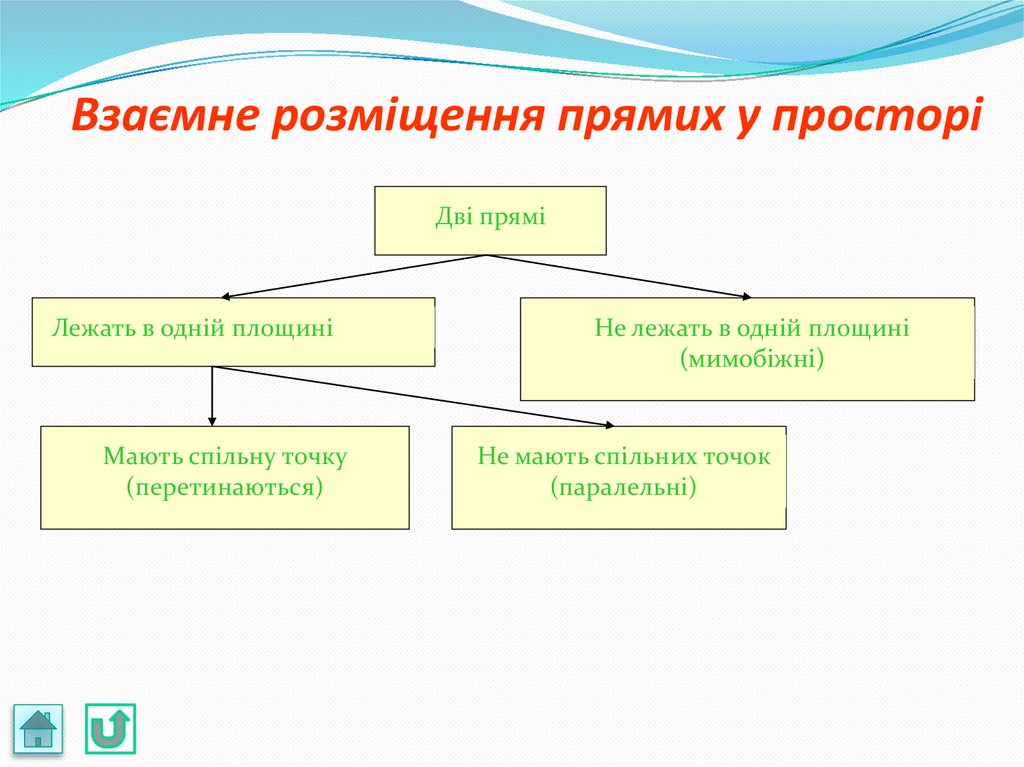
Взаємне розміщення прямих у просторі
Дві прямі
Лежать в одній площині
Мають спільну точку
(перетинаються)
Не лежать в одній площині
(мимобіжні)
Не мають спільних точок
(паралельні)

4.

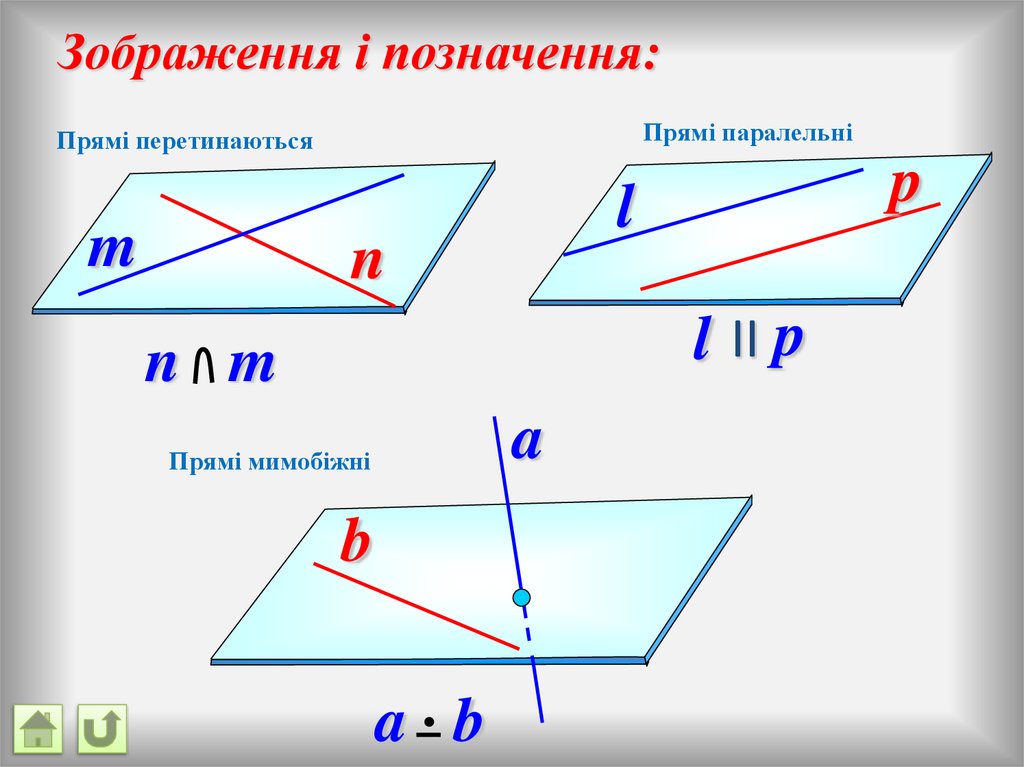
Зображення і позначення:
Прямі паралельні
Прямі перетинаються
m
p
l
n
l II p
n m
a
Прямі мимобіжні
b
a b

5.

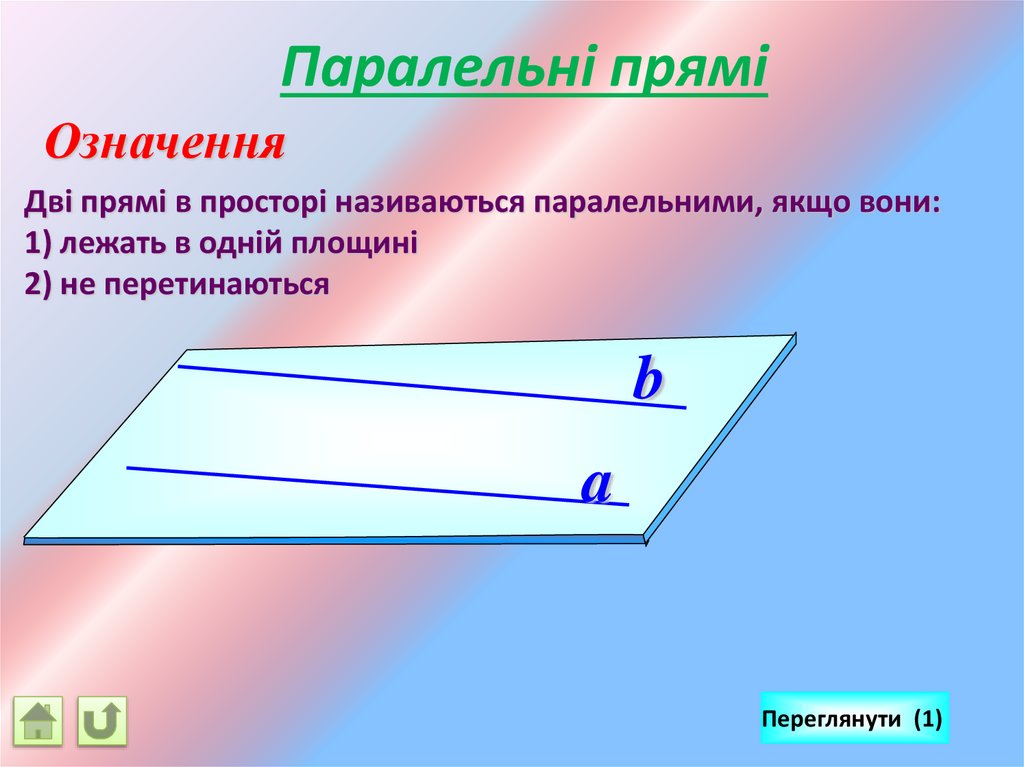
Паралельні прямі
Означення
Дві прямі в просторі називаються паралельними, якщо вони:
1) лежать в одній площині
2) не перетинаються
b
a
Переглянути (1)

6.

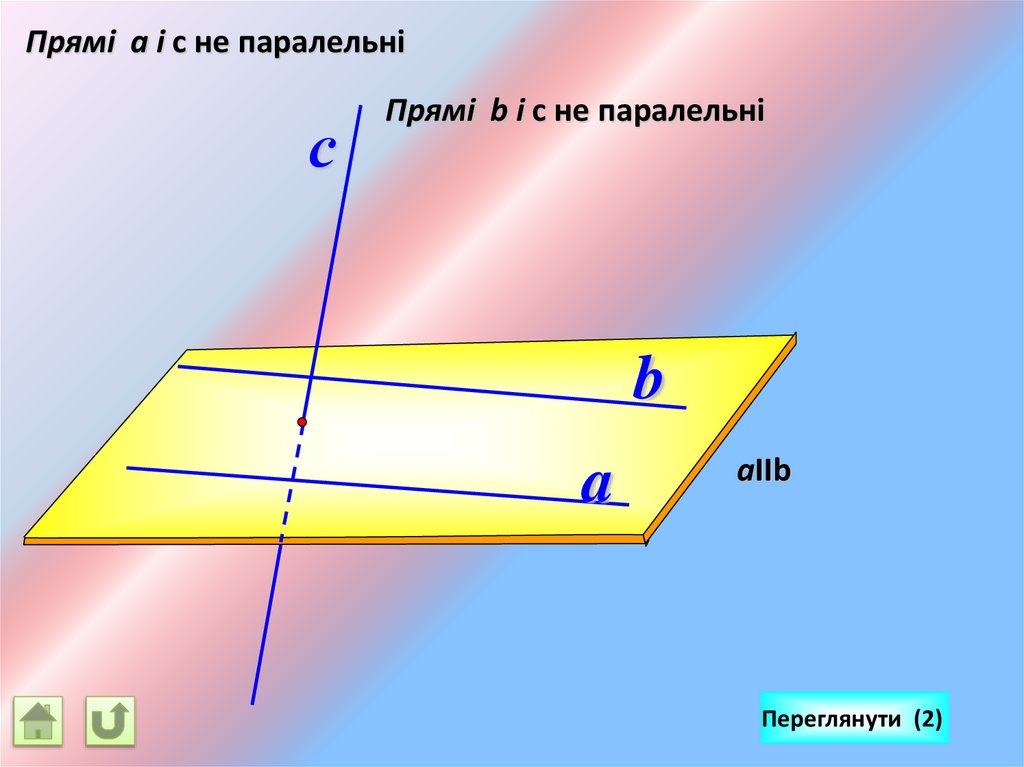
Прямі а і с не паралельні
с
Прямі b і с не паралельні
b
a
aIIb
Переглянути (2)

7.

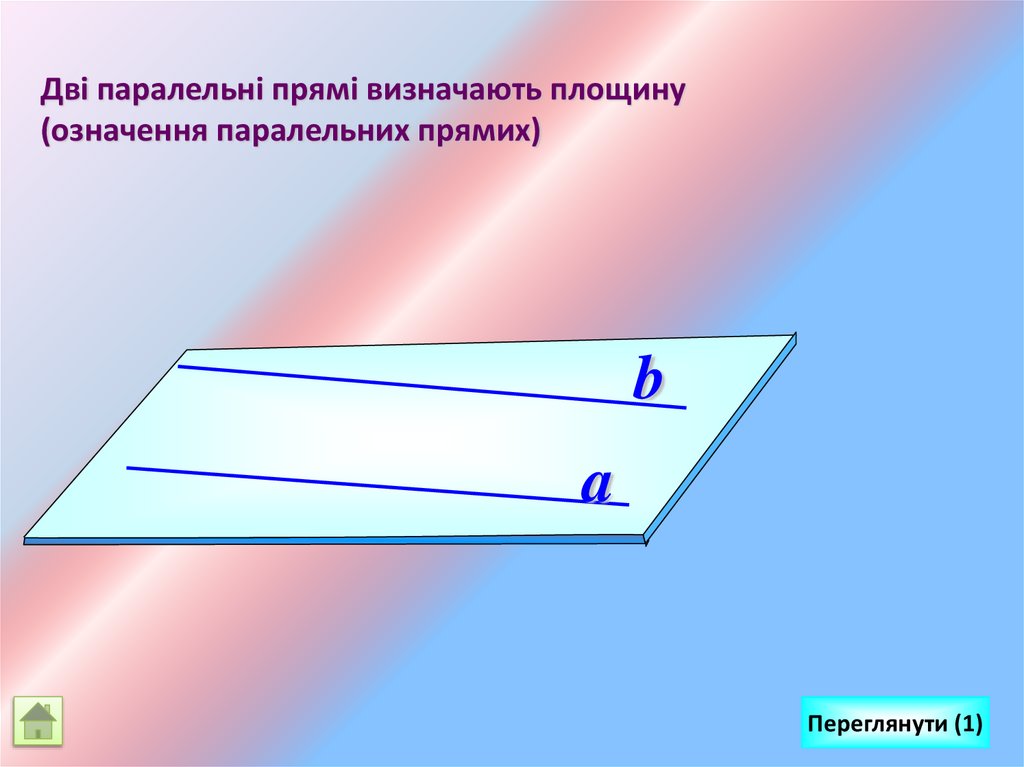
Дві паралельні прямі визначають площину
(означення паралельних прямих)
b
a
Переглянути (1)

8.

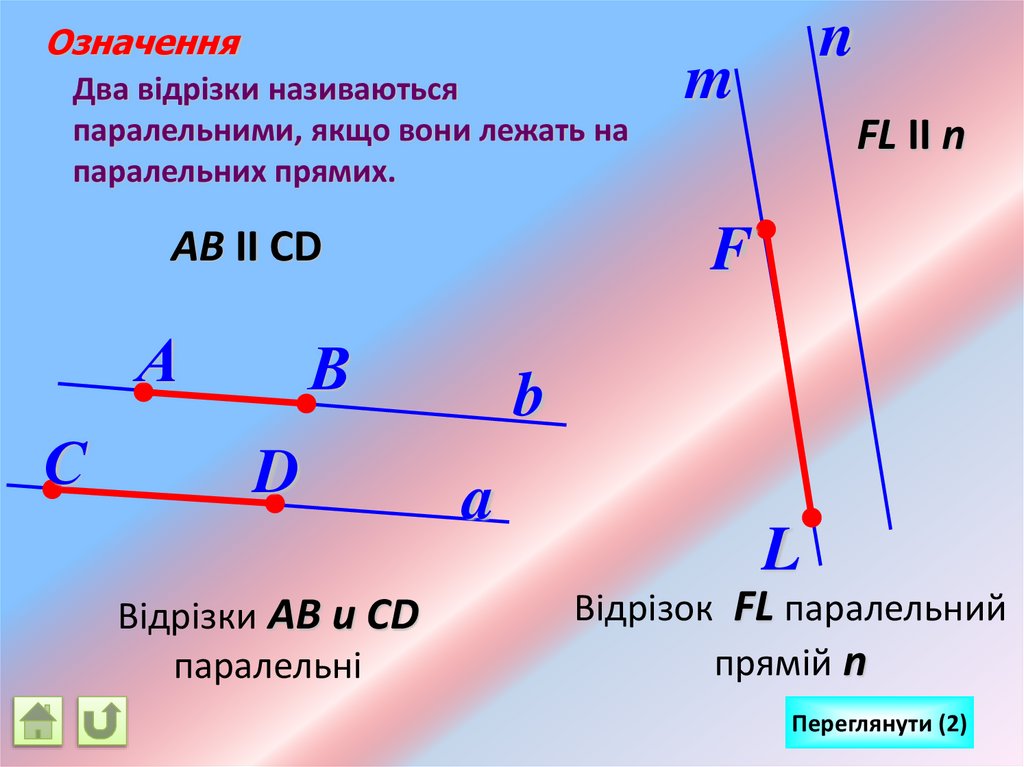
Означення
Два відрізки називаються
паралельними, якщо вони лежать на
паралельних прямих.
АВ II СD
А
С
Відрізки АВ и СD
паралельні
m
FL II n
F
В
D
n
b
a
L
Відрізок FL паралельний
прямій n
Переглянути (2)

9.

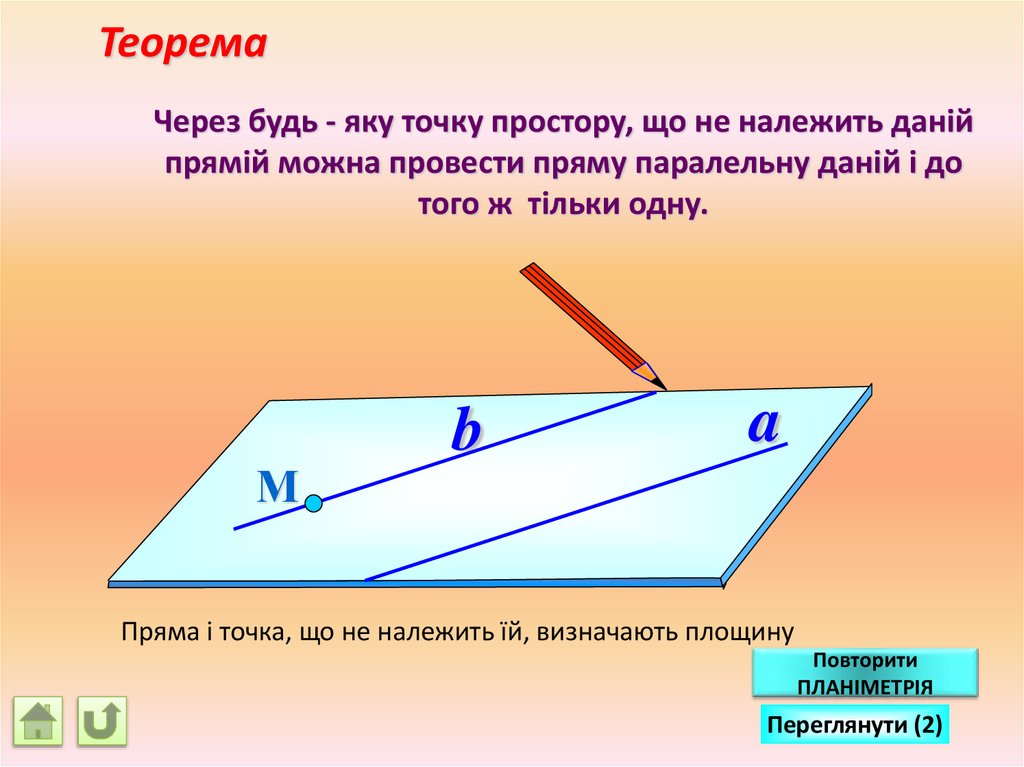
Теорема
Через будь - яку точку простору, що не належить даній
прямій можна провести пряму паралельну даній і до
того ж тільки одну.
М
b
a
Пряма і точка, що не належить їй, визначають площину
Повторити
ПЛАНІМЕТРІЯ
Переглянути (2)

10.

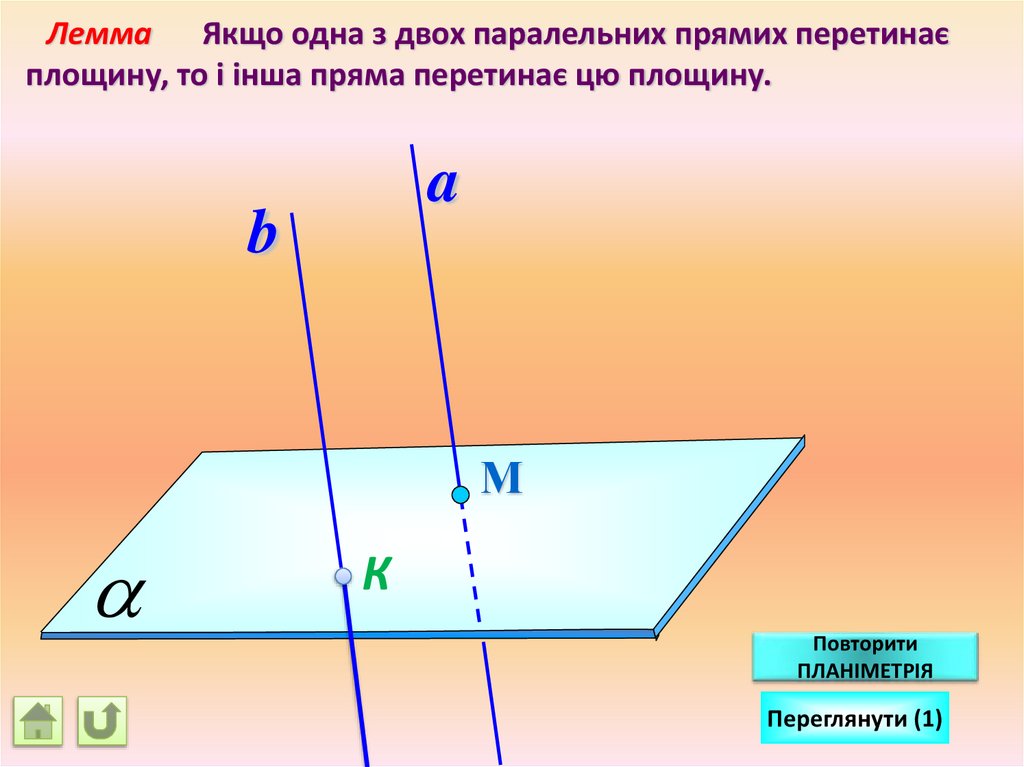
Лемма Якщо одна з двох паралельних прямих перетинає
площину, то і інша пряма перетинає цю площину.
a
b
М
К
Повторити
ПЛАНІМЕТРІЯ
Переглянути (1)

11.

Ознака паралельності прямих
Якщо дві прямі паралельні третій, то вони
паралельні між собою.
с
a
b
К

12.

Мимобіжні прямі
Означення.
Дві прямі в просторі називаються мимобіжними,
якщо вони не лежать в одній

13.

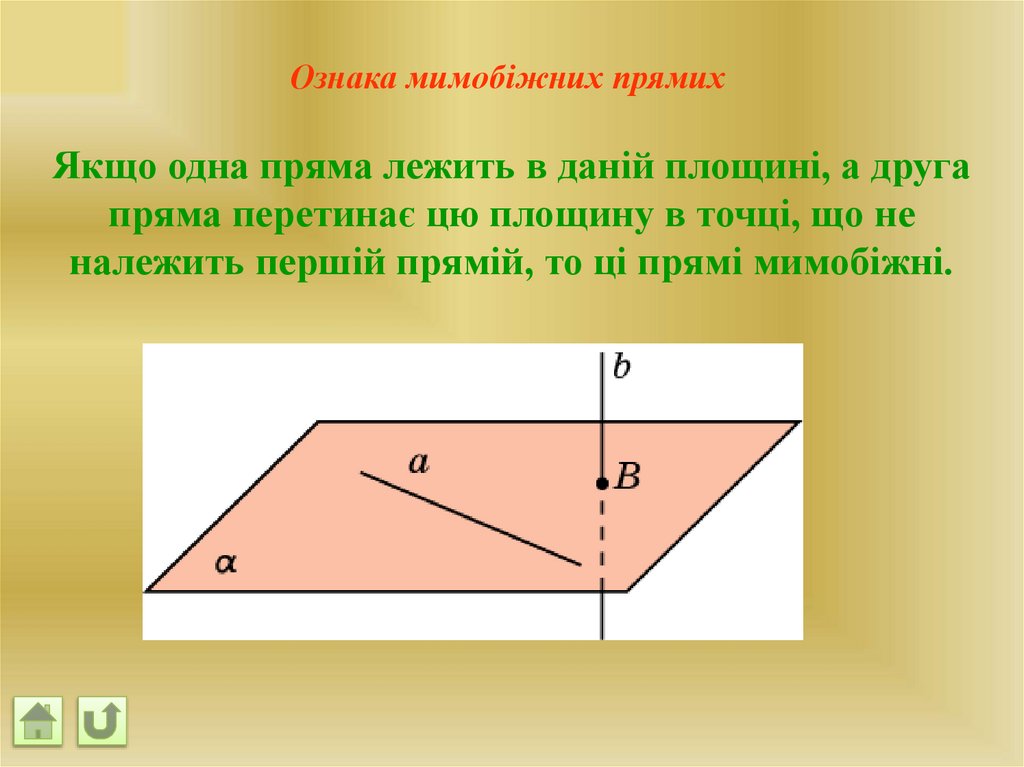
Ознака мимобіжних прямих
Якщо одна пряма лежить в даній площині, а друга
пряма перетинає цю площину в точці, що не
належить першій прямій, то ці прямі мимобіжні.

14.

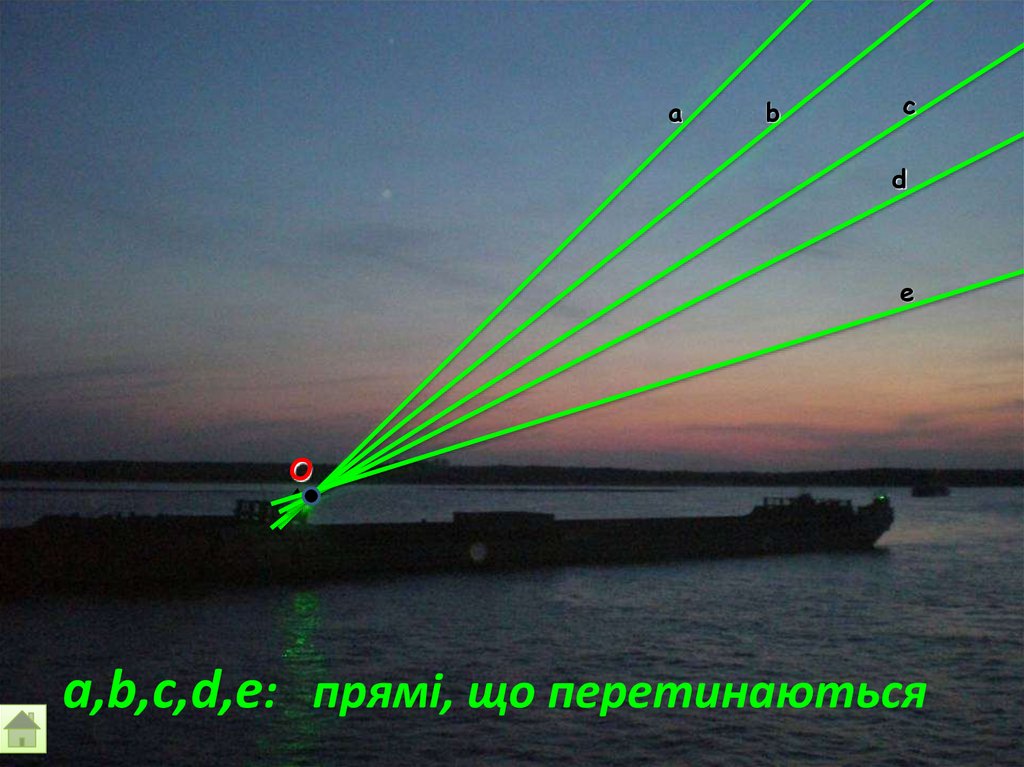
а
b
c
d
e
О
a,b,c,d,e: прямі, що перетинаються

15.

16.

17.

18.

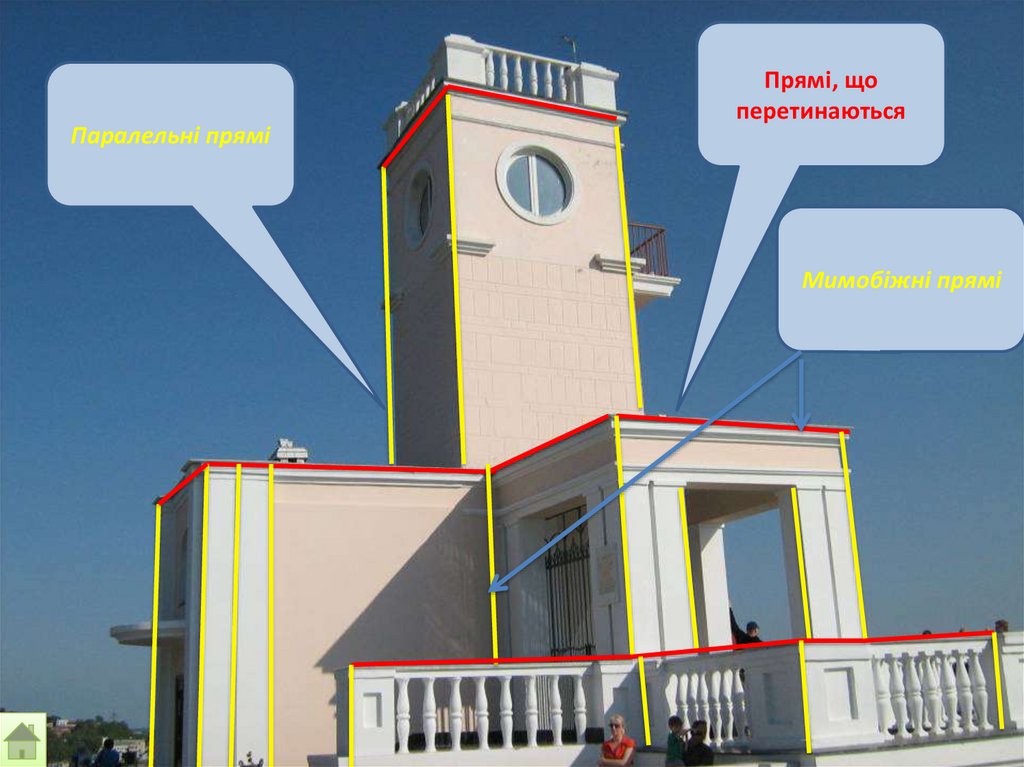
Паралельні прямі
Прямі, що
перетинаються
Мимобіжні прямі

19.

B1
Дано:
A1
K
C1
D1
N
ABCDA1B1C1D1 – КУБ.
P
K, M, N – СЕРЕДИНИ
РЕБЕР
M
B1C1, D1D, D1C1 ВІДПОВІДНО,
B
C
P – ТОЧКА ПЕРЕТИНУ ДІАГОНАЛЕЙ
ГРАНЕЙ AA
B B.
A 1 1
D
ВИЗНАЧТЕ ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХ

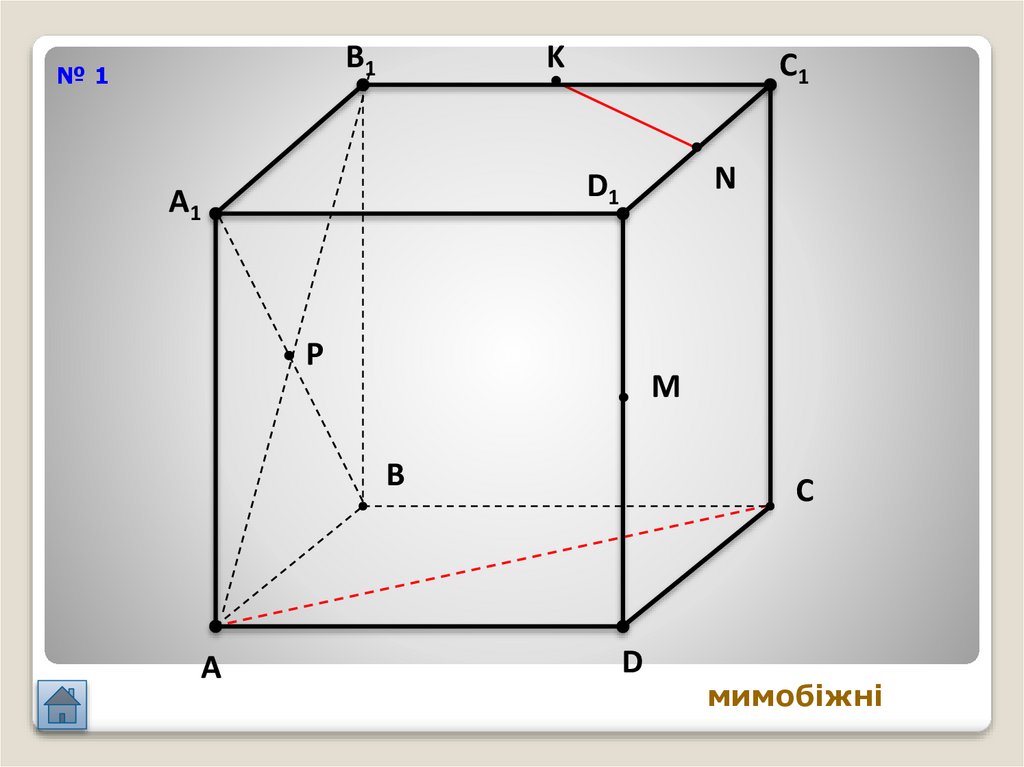
20.

B1
№1
K
C1
N
D1
A1
P
M
B
A
C
D
мимобіжні

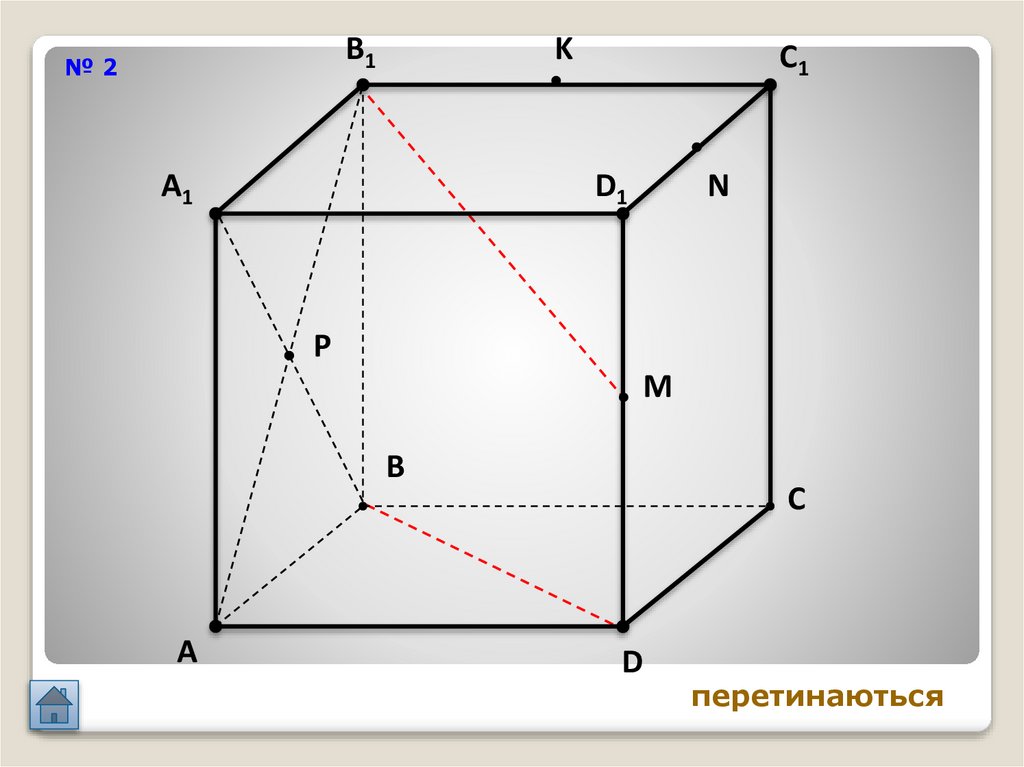
21.

B1
№2
K
A1
C1
D1
N
P
M
B
A
C
D
перетинаються

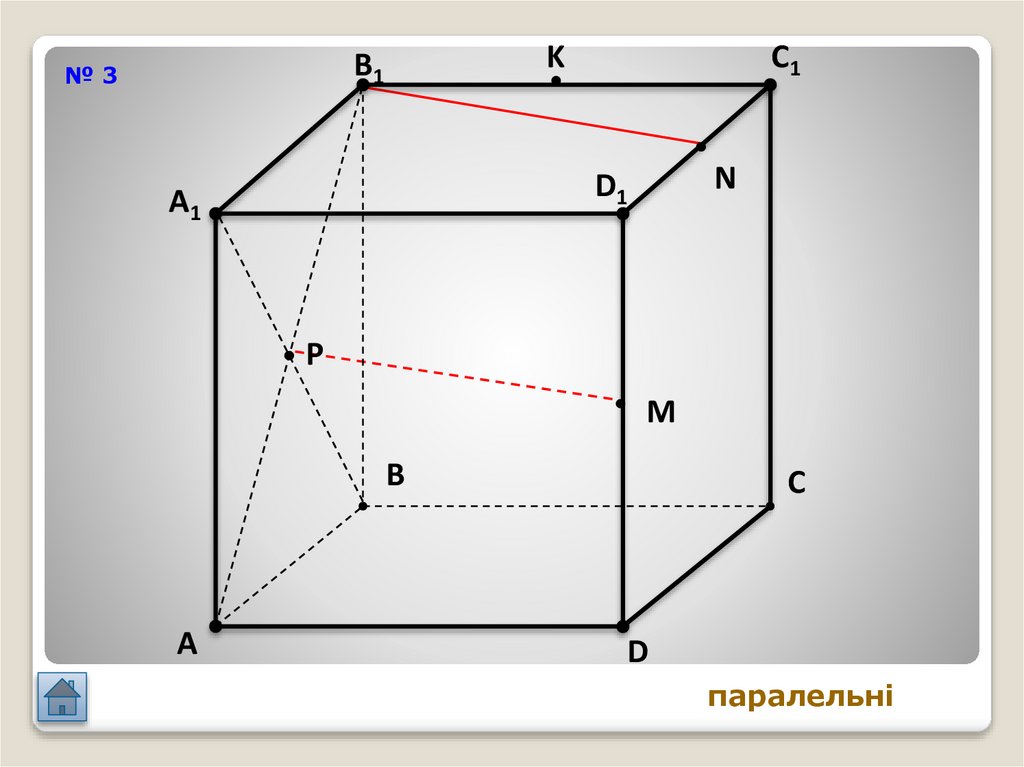
22.

K
B1
№3
C1
N
D1
A1
P
M
B
A
C
D
паралельні

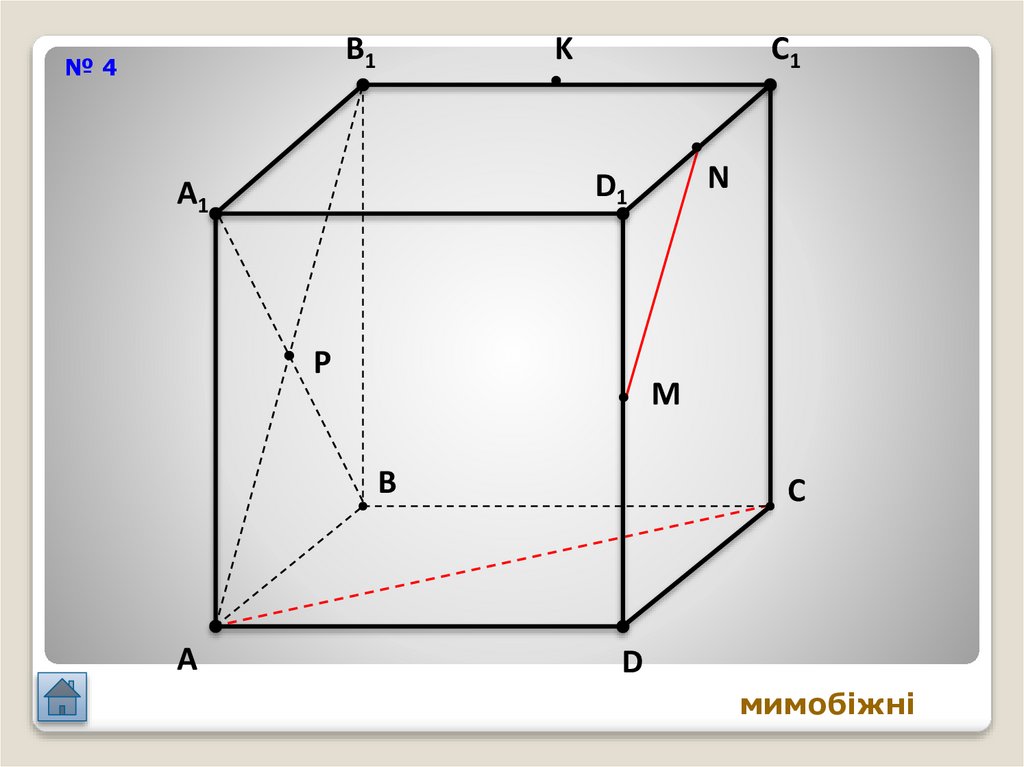
23.

B1
№4
K
C1
P
M
B
A
N
D1
A1
C
D
мимобіжні

24.

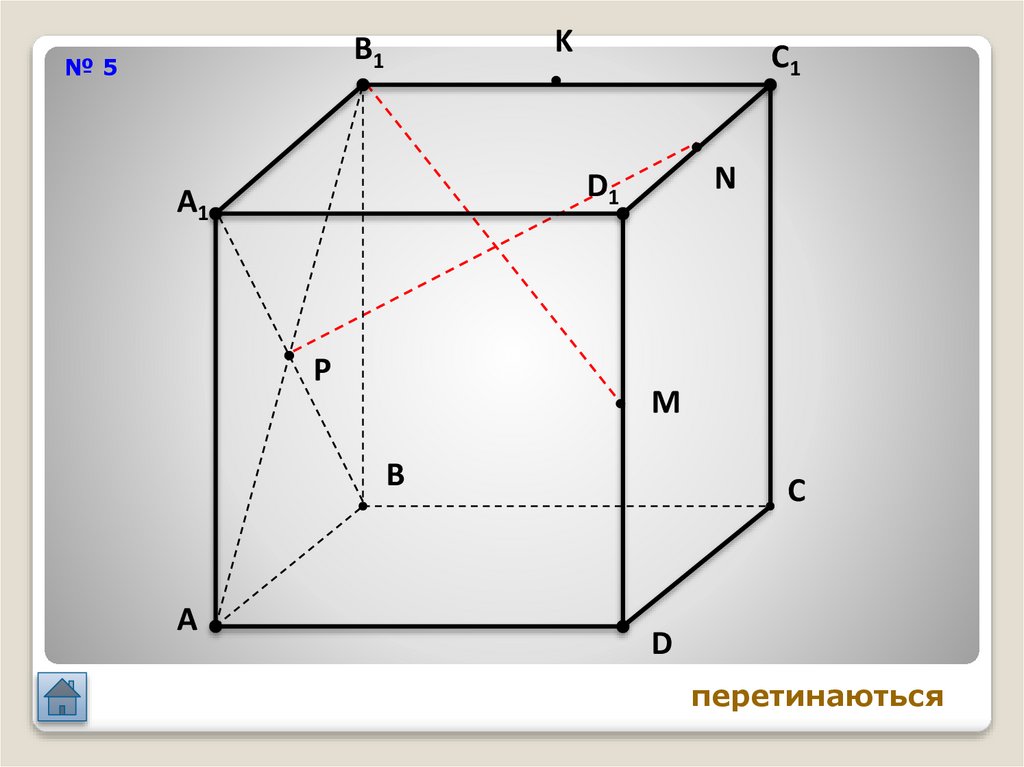
K
B1
№5
C1
N
D1
A1
P
M
B
A
C
D
перетинаються

25.

S
K
M
Дано:
SABC - ТЕТРАЙДР.
ТОЧКИ K, M, N, P – СЕРЕДИНИ РЕБЕР
SA, SC, AB, BC ВІДПОВІДНО.
A
C
N
P
B
ВИЗНАЧТЕ ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХ

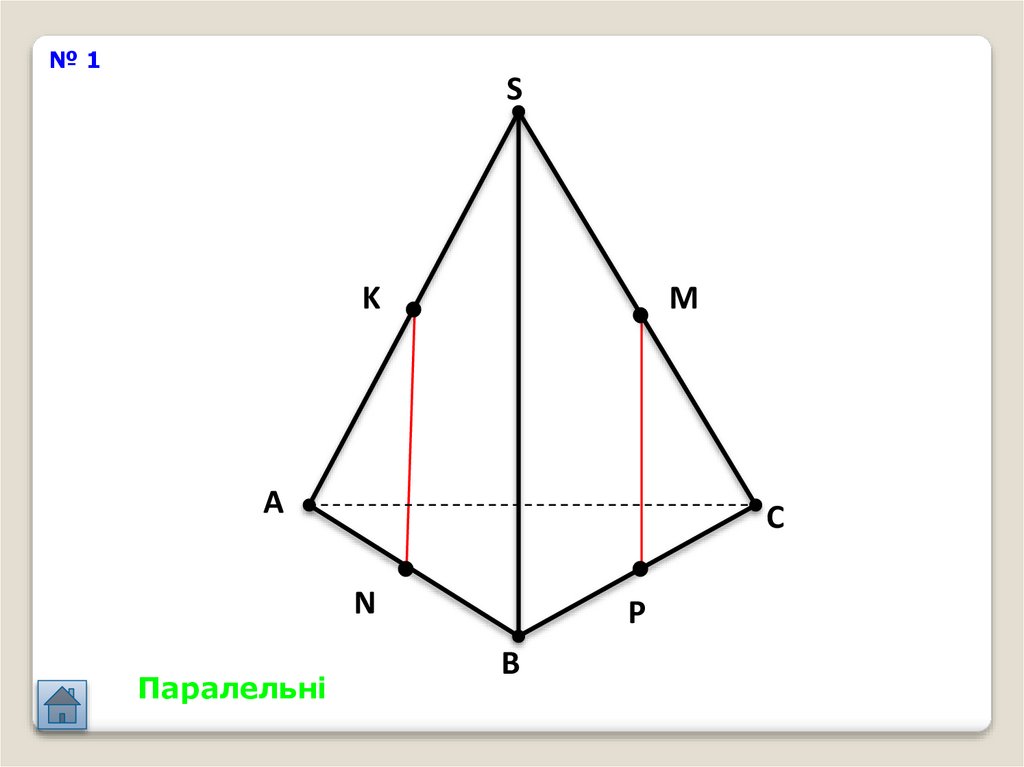
26.

№1
S
K
M
A
C
N
Паралельні
P
B

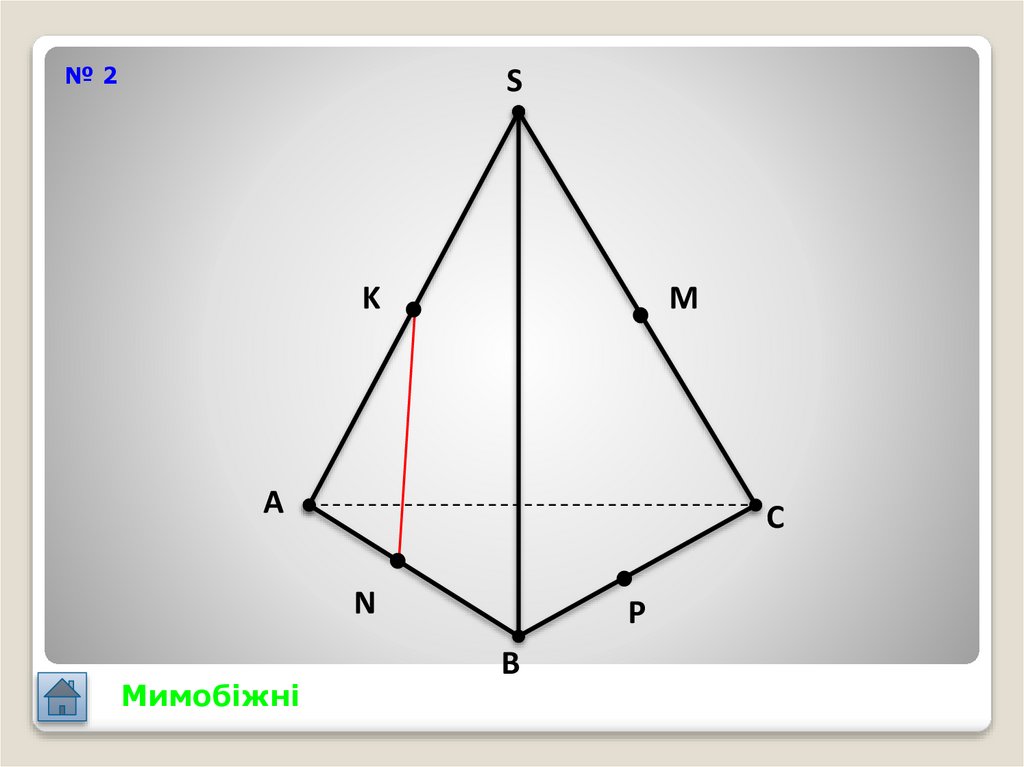
27.

№2
S
K
M
A
C
N
Мимобіжні
P
B

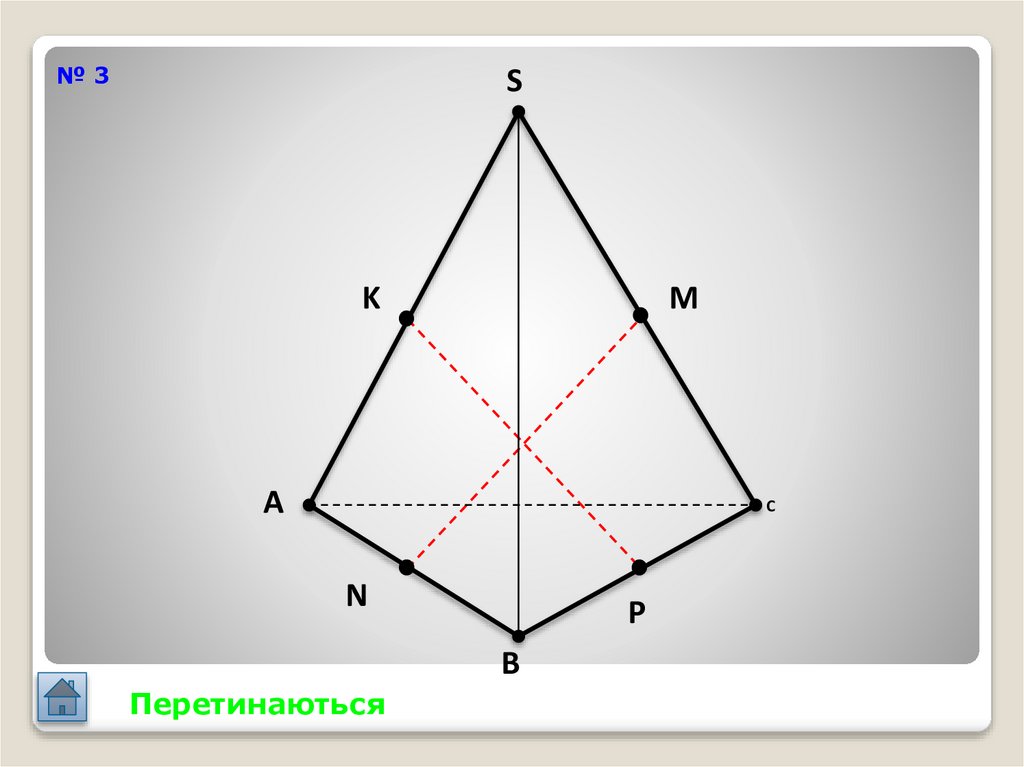
28.

№3
S
K
M
A
C
N
P
B
Перетинаються

29.

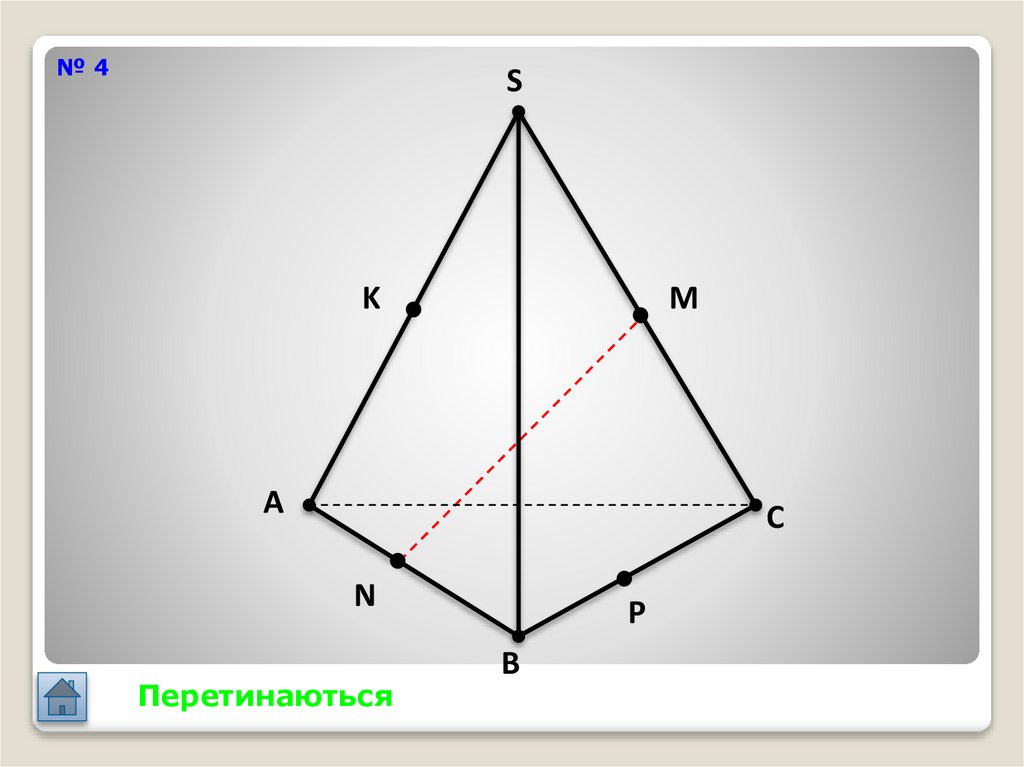
№4
S
K
M
A
C
N
Перетинаються
P
B

30.

Перевір себе
Назвіть взаємне розміщення прямих.
b
а
b
а
b
а

31.

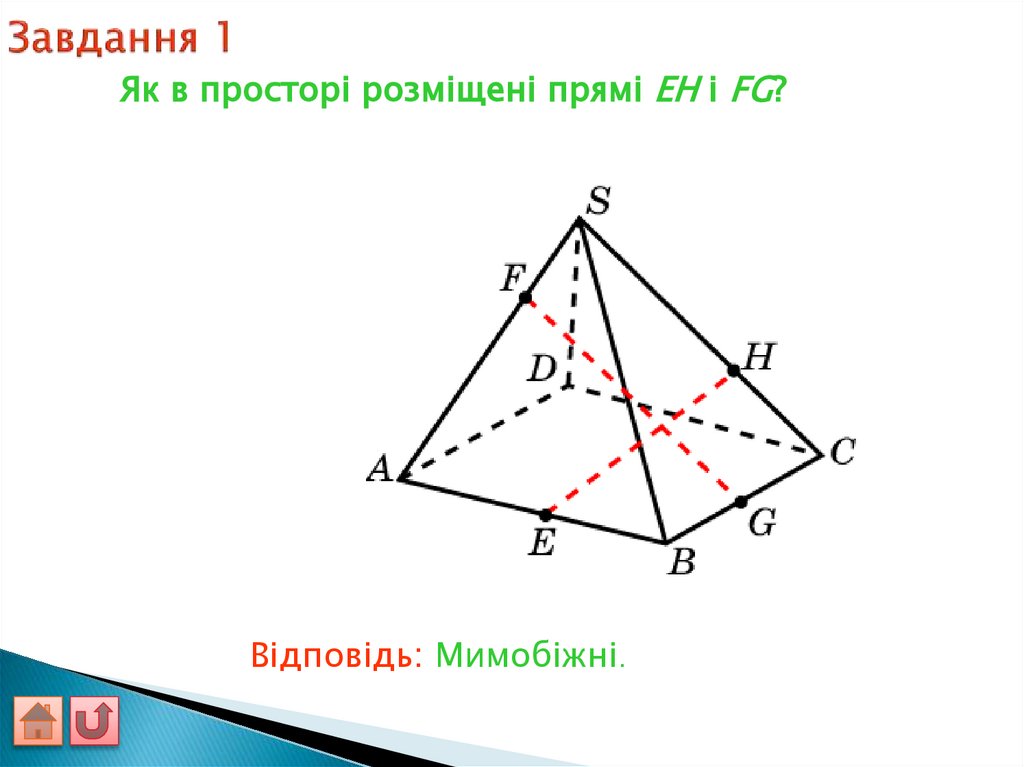
Як в просторі розміщені прямі EH і FG?
Відповідь: Мимобіжні.

32.

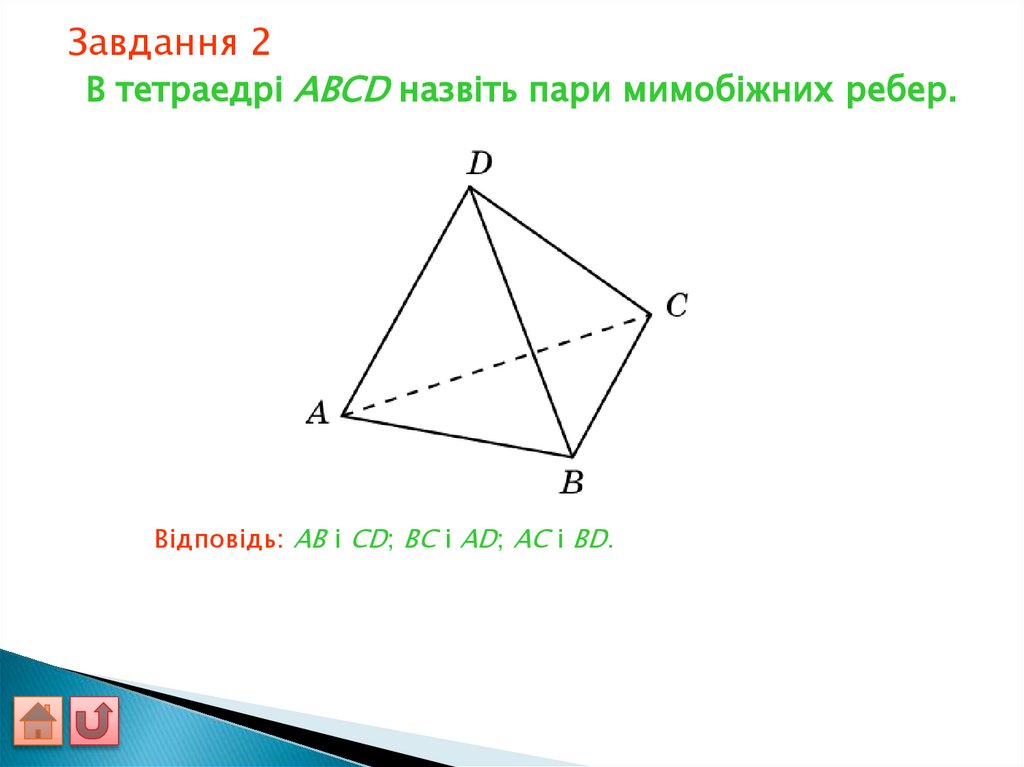
Завдання 2
В тетраедрі ABCD назвіть пари мимобіжних ребер.
Відповідь: AB і CD; BC і AD; AC і BD.

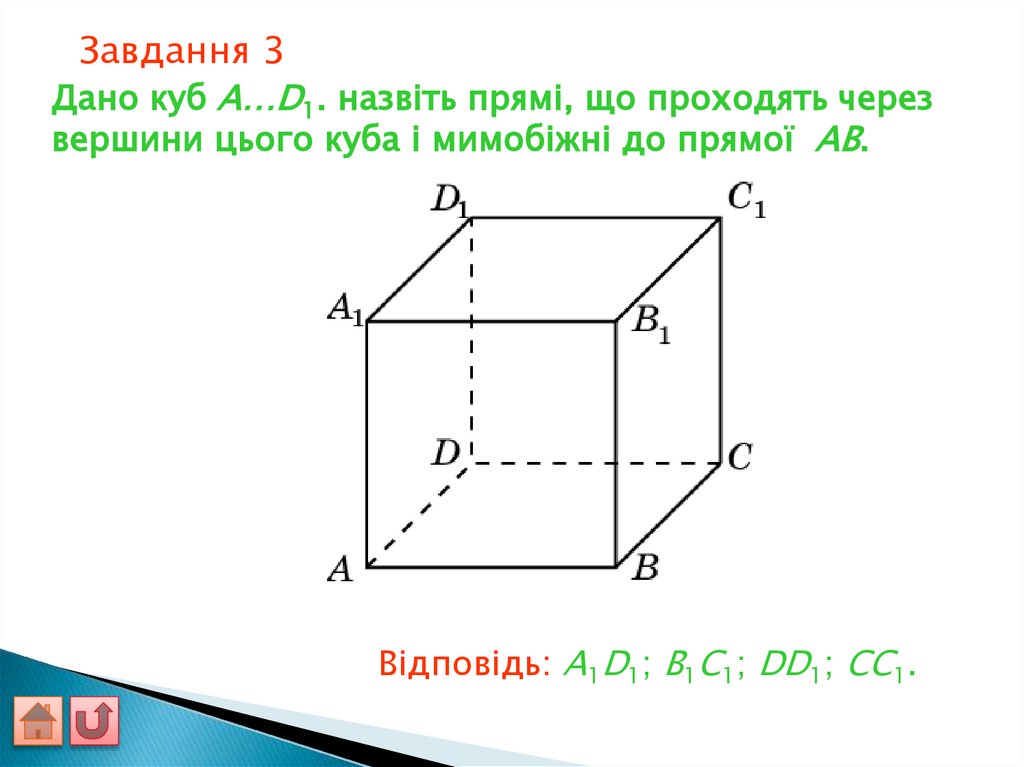
33.

Завдання 3
Дано куб A…D1. назвіть прямі, що проходять через
вершини цього куба і мимобіжні до прямої AB.
Відповідь: A1D1; B1C1; DD1; CC1.

34.

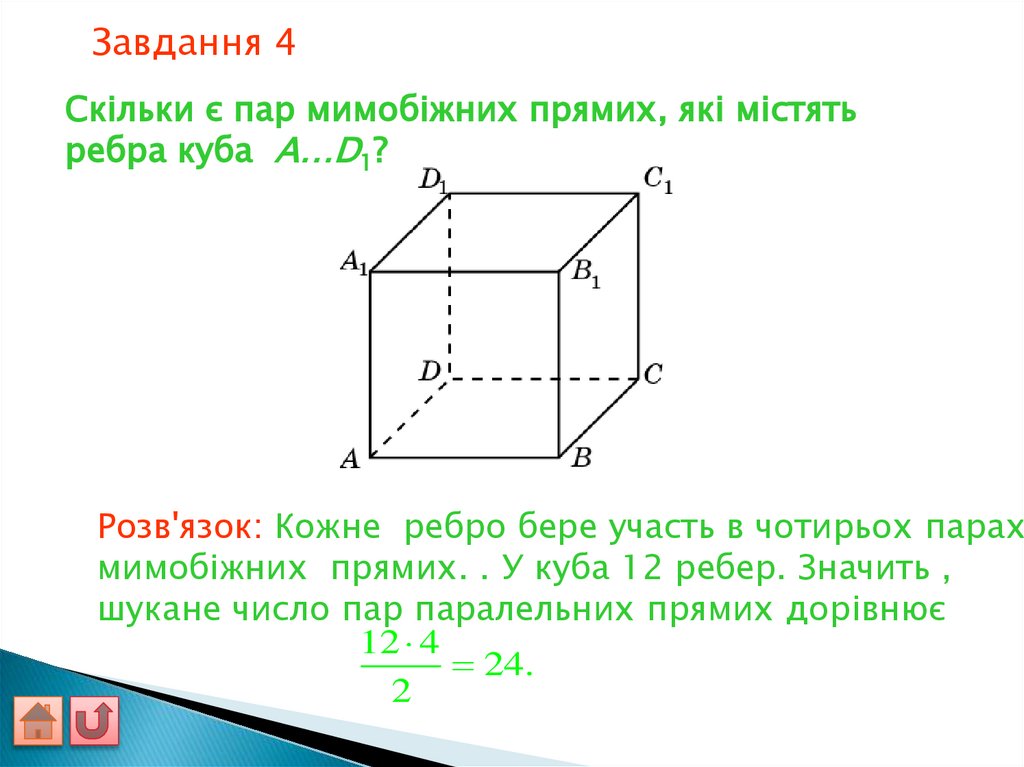
Завдання 4
Скільки є пар мимобіжних прямих, які містять
ребра куба A…D1?
Розв'язок: Кожне ребро бере участь в чотирьох парах
мимобіжних прямих. . У куба 12 ребер. Значить ,
шукане число пар паралельних прямих дорівнює
12 4
24.
2

35.

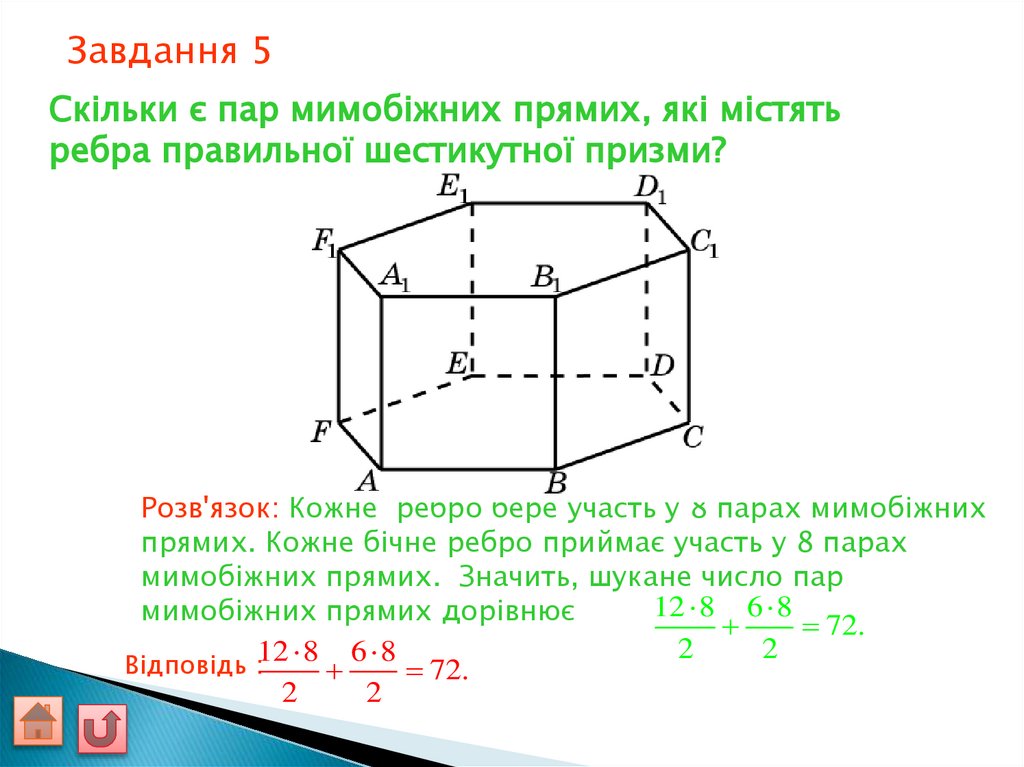
Завдання 5
Скільки є пар мимобіжних прямих, які містять
ребра правильної шестикутної призми?
Розв'язок: Кожне ребро бере участь у 8 парах мимобіжних
прямих. Кожне бічне ребро приймає участь у 8 парах
мимобіжних прямих. Значить, шукане число пар
12 8 6 8
мимобіжних прямих дорівнює
72.
2
2
12 8 6 8
Відповідь :
72.
2
2

36.

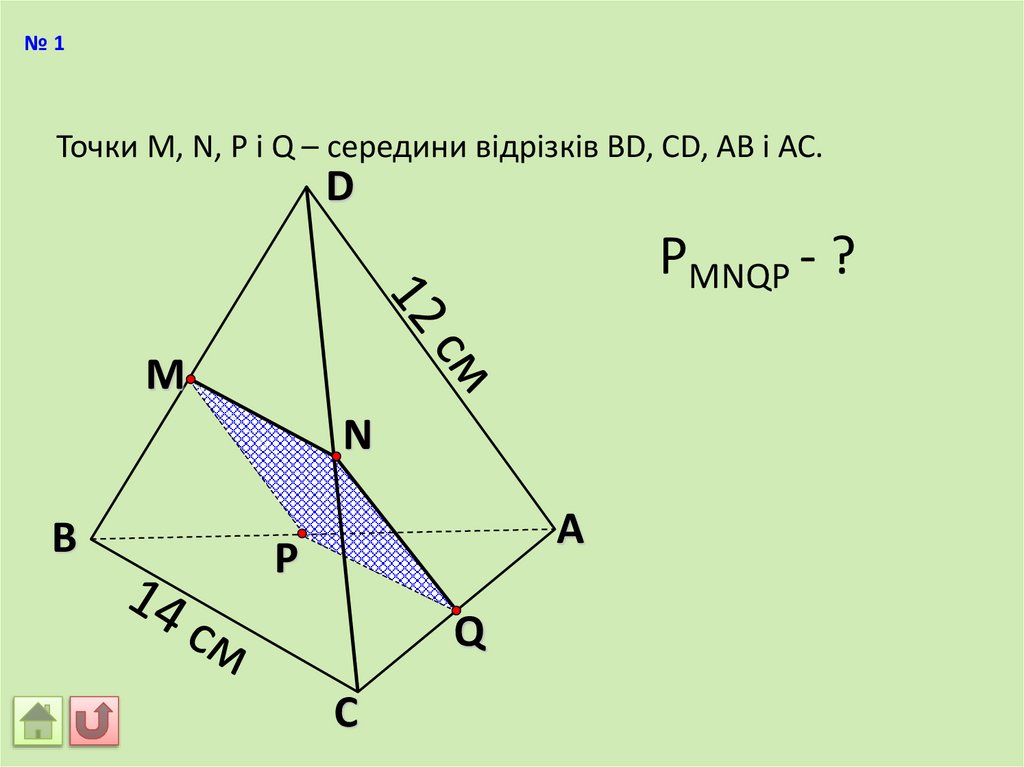
№1
Точки М, N, P і Q – середини відрізків BD, CD, AB і АС.
D
РMNQP - ?
M
N
В
А
P
Q
С

37.

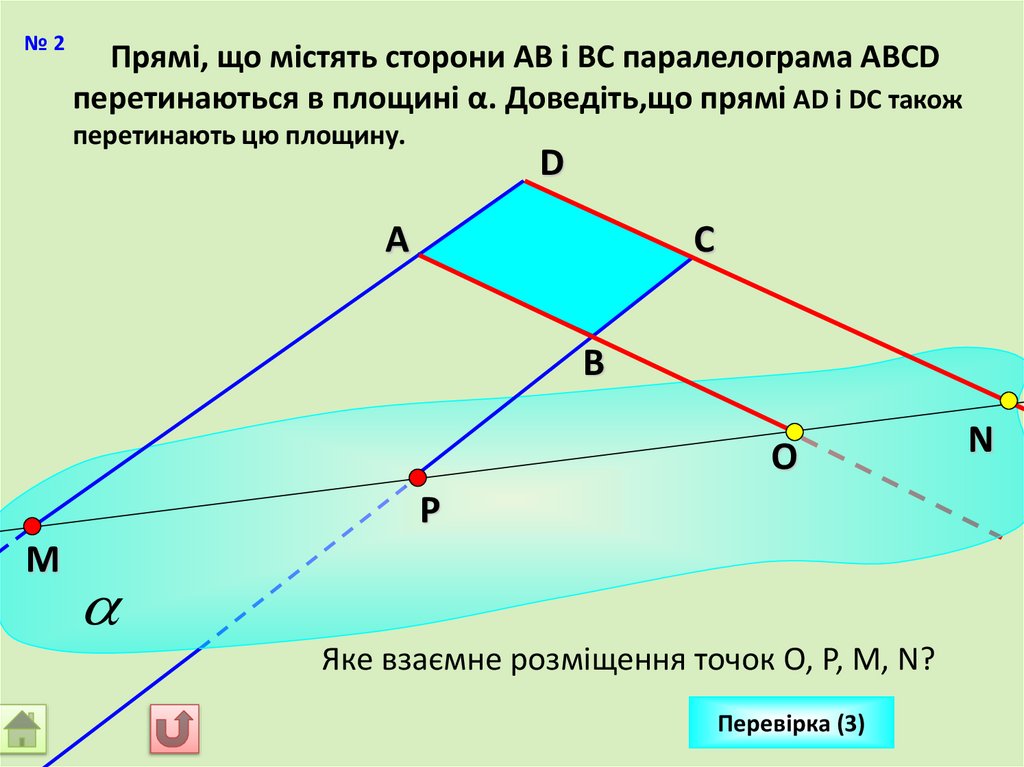
№2
Прямі, що містять сторони АВ і ВС паралелограма АВСD
перетинаються в площині α. Доведіть,що прямі AD і DC також
перетинають цю площину.
D
А
С
В
О
Р
М
Яке взаємне розміщення точок О, Р, М, N?
Перевірка (3)
N

38.

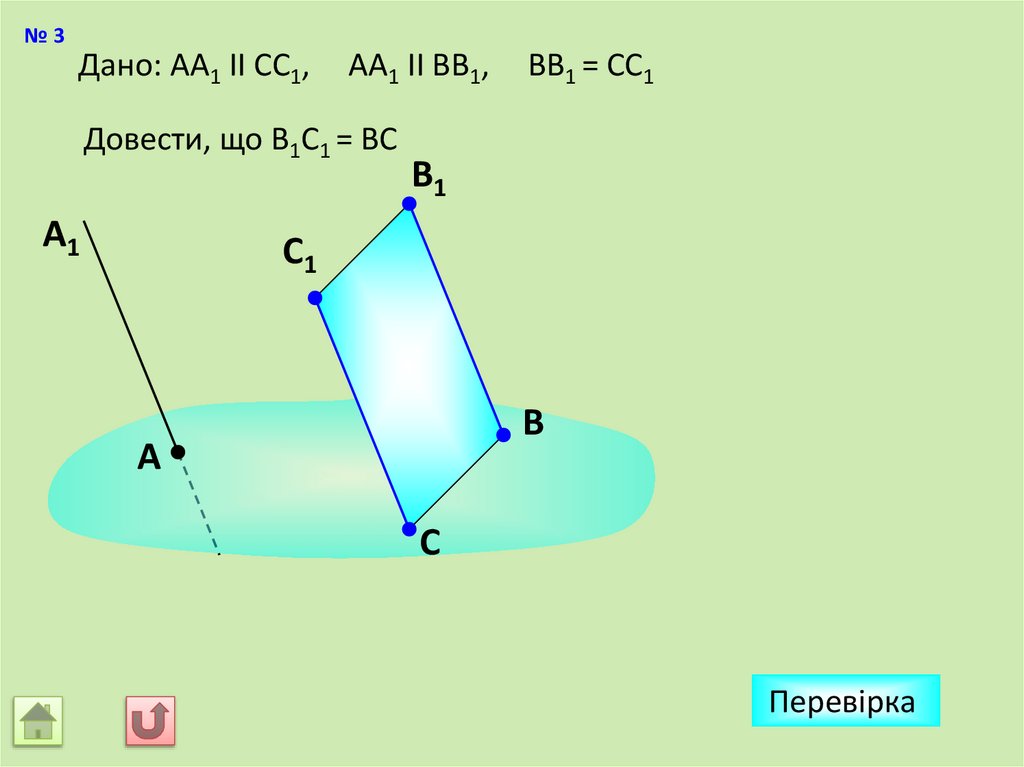
№3
Дано: АА1 II СС1,
АА1 II ВВ1,
Довести, що В1С1 = ВС
А1
ВВ1 = СС1
В1
С1
В
А
С
Перевірка

39.

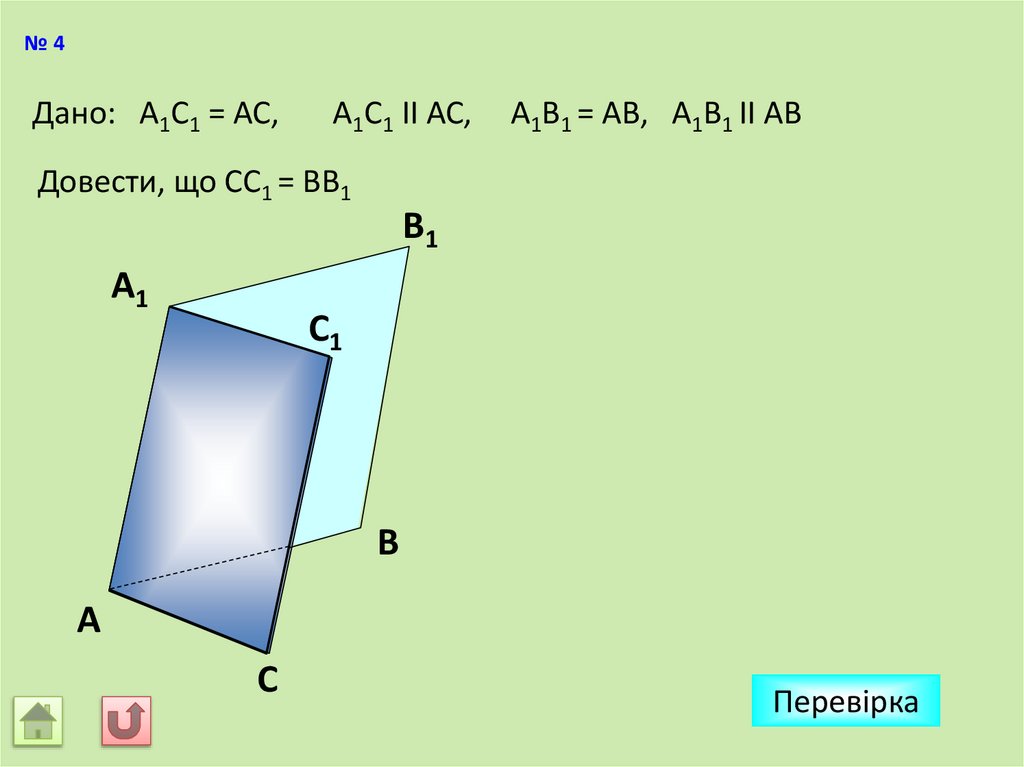
№4
Дано: А1С1 = АС,
А1С1 II АС,
А1В1 = АВ, А1В1 II АВ
Довести, що CС1 = ВB1
В1
А1
С1
В
А
С
Перевірка

40.

Трикутник АВС і квадрат АEFC не лежать в одній
площині. Точки К і М – середини відрізків АВ и ВС відповідно.
Доведіть, що КМ II EF.
Знайдіть КМ, якщо АЕ=8см.
№5
В
M
K
С
А
F
8см
Е

41.

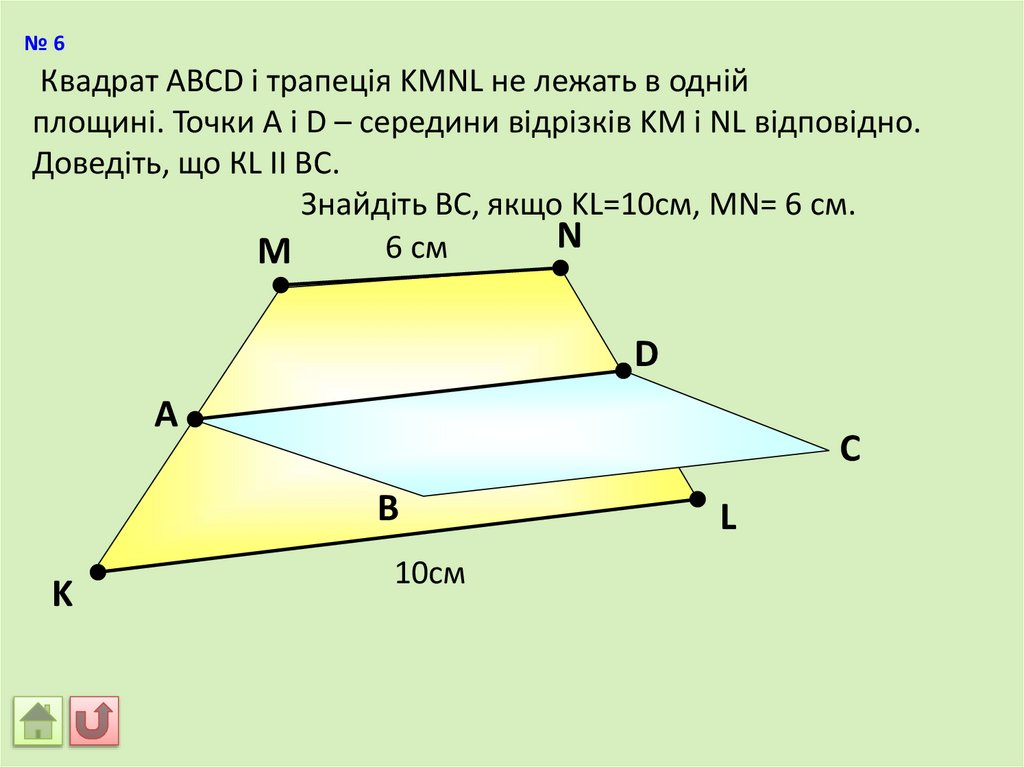
№6
Квадрат АВСD і трапеція KMNL не лежать в одній
площині. Точки A і D – середини відрізків KM і NL відповідно.
Доведіть, що КL II BC.
Знайдіть BC, якщо KL=10см, MN= 6 см.
N
6 см
M
D
А
В
K
С
С
10см
L

42.

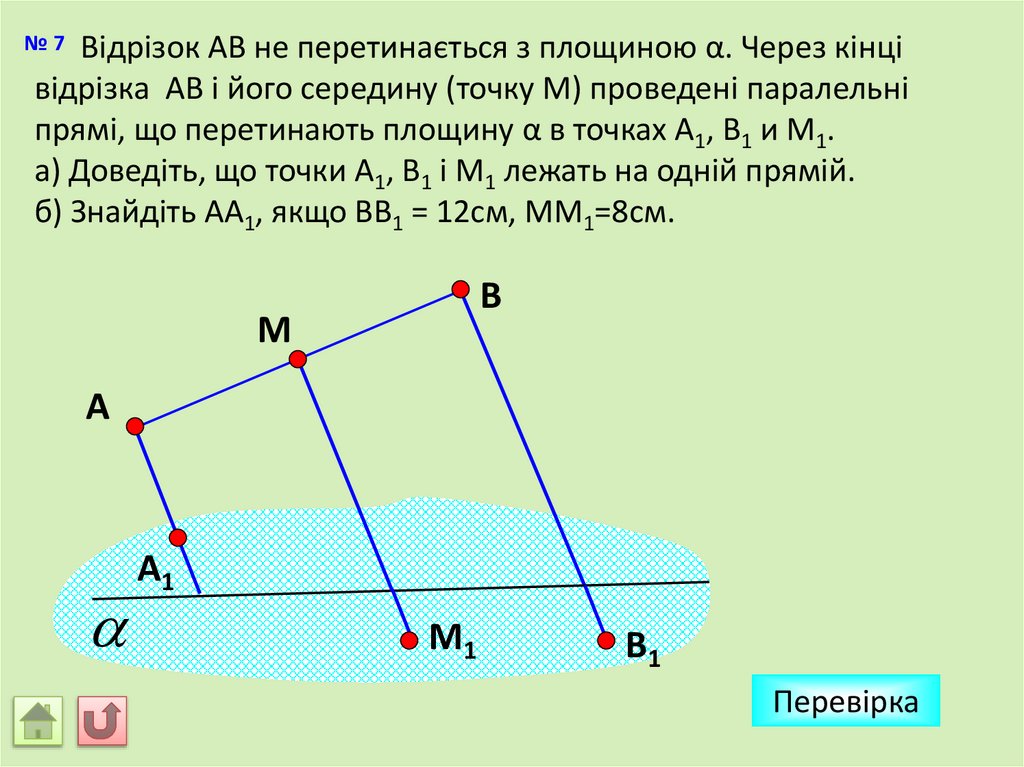
№ 7 Відрізок АВ не перетинається з площиною α. Через кінці
відрізка АВ і його середину (точку М) проведені паралельні
прямі, що перетинають площину α в точках А1, В1 и М1.
а) Доведіть, що точки А1, В1 і М1 лежать на одній прямій.
б) Знайдіть АА1, якщо ВВ1 = 12см, ММ1=8см.
В
М
А
А1
M1
В1
Перевірка