Similar presentations:
Электромагнетизм
1.
ЭЛЕКТРОМАГНЕТИЗМ2.
ЭЛЕКТРОСТАТИКА3.
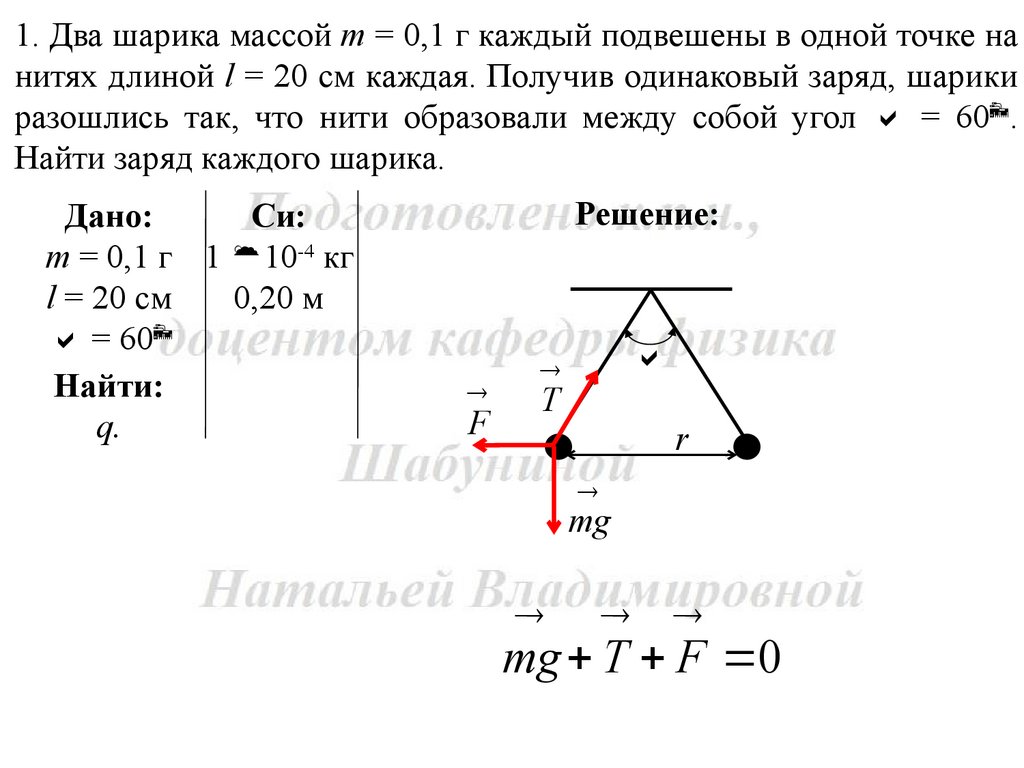
1. Два шарика массой m = 0,1 г каждый подвешены в одной точке нанитях длиной l = 20 см каждая. Получив одинаковый заряд, шарики
разошлись так, что нити образовали между собой угол = 60 .
Найти заряд каждого шарика.
Си:
Дано:
m = 0,1 г 1 10-4 кг
0,20 м
l = 20 см
= 60
Найти:
q.
Решение:
F
T
r
mg
mg T F 0
4.
yT
F
x
r
mg
x : F Tsin 0
2
y : Tcos mg 0
2
Tsin F
2
Tcos mg
2
F
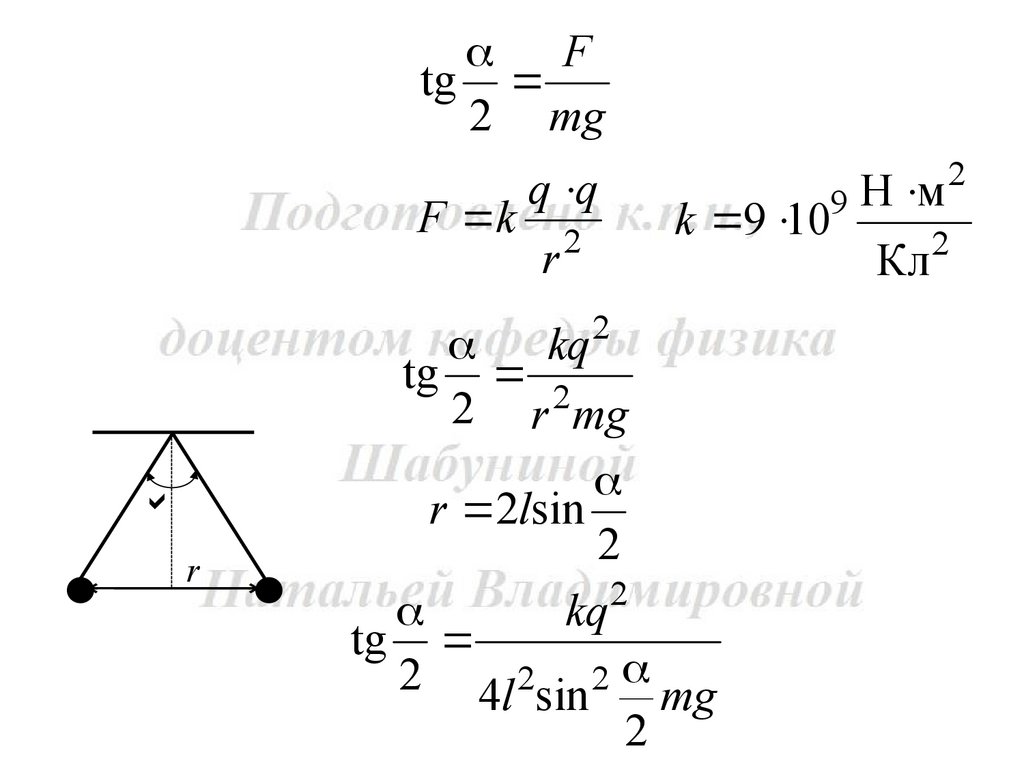
tg
2 mg
5.
Ftg
2 mg
F k
q q
r
2
2
r
9
k 9 10
kq
tg 2
2 r mg
r 2lsin
2
kq 2
tg
2 4l 2sin 2 mg
2
Н м
Кл
2
2
6.
2kq
tg
2 4l 2sin 2 mg
2
2
2
4l sin
mg tg
2
2
q
k
mg tg
2
q 2lsin
2
k
q 2 0,20 sin30
1 10
4
10 tg30
9
9 10
50нКл
7.
2. Тонкий стержень длиной 10 см равномерно заряжен. Линейнаяплотность заряда равна 103 нКл/м. На продолжении оси стержня
на расстоянии 20 см от ближайшего его конца находится точечный
заряд Q = 100 нКл. Определить силу взаимодействия заряженного
стержня и точечного заряда.
Дано:
Си:
l = 10 см
0,10 м
= 103 нКл/м1 10-6 Кл/м
0,20 м
а = 20 см
Q = 100 нКл 100 10-9 Кл
Найти:
F.
Решение:
Q
dq
0
X
x
dx
dq dx
dF
F dF
8.
dq0
dx
Q
x
X
F dF
dq Q
dF k 2
x
dq Q
dx Q
F dF k 2 k
2
x
x
9.
dq0
dx
Q
x
X
a l dx
dx Q
1 a l
k
Q
|
k
Q
k
2
2
a
x a
x
x
1
1
k Q
a a l
1
1
F k Q
a a l
10.
11
F k Q
a a l
1
1
F 9 10 10 100 10
1,5мН
0,20 0,20 0,10
9
6
9
11.
3. Электрическое поле создано двумя точечными зарядами Q1= 40нКл и Q2= - 10 нКл, находящимися на расстоянии d = 10 см друг от
друга. Определить напряжённость поля в точке, удалённой от
первого заряда на r1= 12 см и от второго на r2= 6 см.
Дано:
Си:
Q1= 40 нКл 40 10-9 Кл
Q2= - 10 нКл -10 10-9 Кл
0,10 м
d = 10 см
0,12 м
r1= 12 см
0,06 м
r2= 6 см
Найти:
Е.
Решение:
Q1
- Q2
d
E2
r2
r1
EA
A
E1
E A E1 E2
12.
Q1- Q2
d
r2
r1
E2
A
EA
E1
2
EA
d
2
E1
2
2
r1
2
E2
2
r2
arccos
2 E1 E2 cos
2r1 r2 cos
r12 r22 d 2
2r1 r2
13.
arccosr12 r22 d 2
2r1 r2
0,122 0,062 0,102
arccos
56
2 0,12 0,06
180 180 56 124
E1
k Q1
r12
E2
k Q2
r22
14.
E1k Q1
E2
r12
k Q2
r22
9 109 40 10 9
E1
25кН/Кл
2
0,12
9
9 10 10 10
E2
0,062
EA
2
E1
2
E2
9
25кН/Кл
2 E1 E2 cos
15.
EA2
E1
2
E2
2 E1 E2 cos
E A 252 252 2 25 25 cos124 34кН/Кл
16.
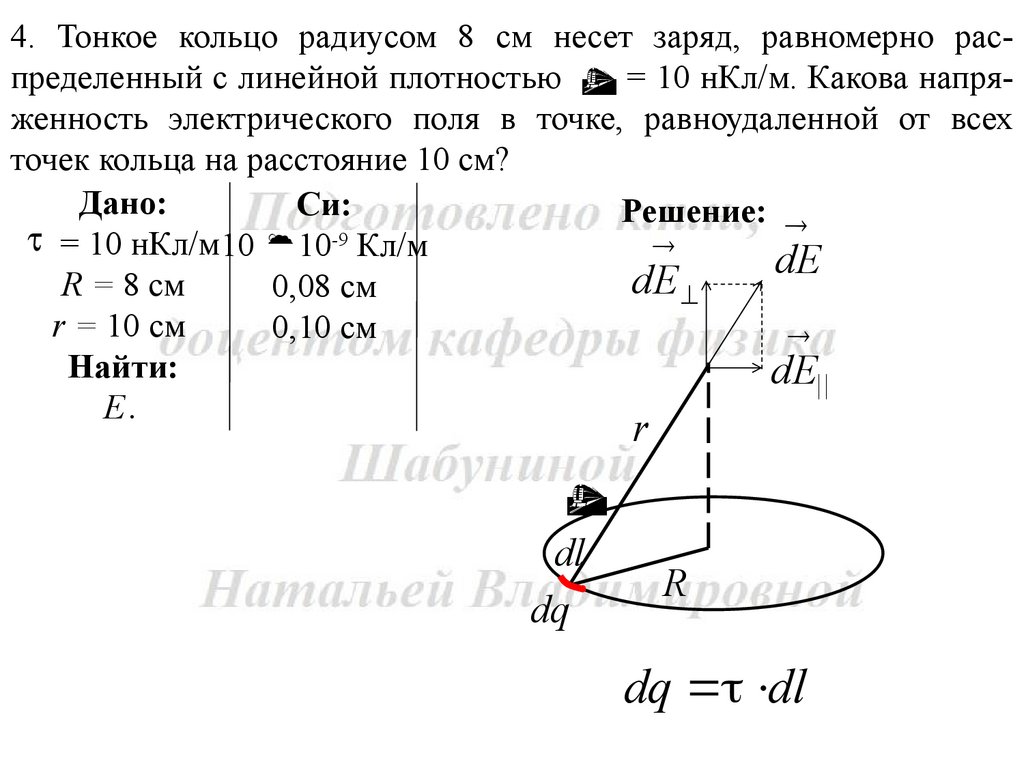
4. Тонкое кольцо радиусом 8 см несет заряд, равномерно распределенный с линейной плотностью = 10 нКл/м. Какова напряженность электрического поля в точке, равноудаленной от всехточек кольца на расстояние 10 см?
Дано:
Си:
Решение:
t = 10 нКл/м 10 10-9 Кл/м
dE
dE
R = 8 см
0,08 см
r = 10 см
0,10 см
Найти:
dE||
Е.
r
dl
dq
R
dq dl
17.
dEdE
E dE dE||
dE||
r
dl
dq
E|| dE|| 0
E E dE
R
dq
E dE dEcos k 2 cos
r
2
2
2
r R
dl r R
k 2
k
3
r
r
r
2
dl
18.
kr
2
2 2 R
R
dl
3
0
r
2
2
2
r R
k
2 R
3
r
2
r R
E k
2 R
3
r
9
9
E 9 10 10 10
2
2
0,10 0,08
6,28 0,08 2,7кН / м
3
0,10
19.
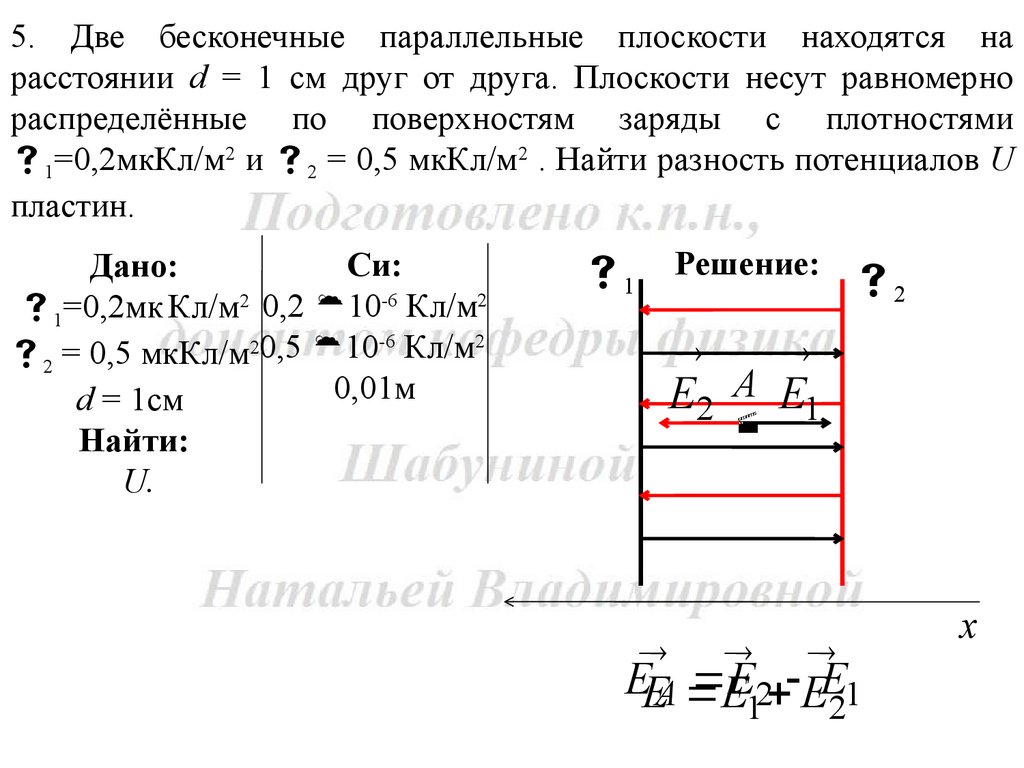
5. Две бесконечные параллельные плоскости находятся нарасстоянии d = 1 см друг от друга. Плоскости несут равномерно
распределённые по поверхностям заряды с плотностями
1=0,2мкКл/м2 и 2 = 0,5 мкКл/м2 . Найти разность потенциалов U
пластин.
Си:
Дано:
1=0,2мк Кл/м2 0,2 10-6 Кл/м2
2 = 0,5 мкКл/м20,5 10-6 Кл/м2
0,01м
d = 1см
Найти:
U.
1 Решение: 2
E2 А E1
EEA
EE2 EE1
1
2
x
20.
E A E2 E11
E1
2 0
2
E2
2 0
1; 0 8,85 10
12
2 1
EA
2 0
U E d
(σ 2 σ1 ) d
U
2 0
Ф/м
21.
(σ 2 σ1 ) dU
2 0
-6
U
(0,5 0,2) 10 0 ,01
2 8,85 10 12
169 В
22.
6. Электрическое поле создано равномерно распределённым покольцу зарядом ( = 103 нКл/м). Определить работу А12 сил поля по
перемещению заряда Q = 10 нКл из точки 1 (в центре кольца) в
точку 2, находящуюся на перпендикуляре к плоскости кольца.
Дано:
Си:
Решение:
= 103 нКл/м1 10-6 Кл/м
2
-9
Q = 10 нКл 10 10 Кл
Найти:
R
А12 .
dq
dl
1
R
A12 Q ( 1 - 2 )
dq dl
23.
dq dl2
r2
R
dq
r1
1
R
k dq
d
r
k dq
d
r
k dq
k dq
1
r1
R
k dq
k dq
2
r2
2R
24.
k dq k dl k1
R
R
R
2 R
k 2 R
dl R 2 k
0
1 2 k
k dq k dl k 2 R
k 2 R
2
dl
2 k
2R
2R
2R 0
2R
2 2 k
A12 Q k (2 - 2 )
25.
A12 Q k ( 2 - 2 )A12 10 10 9 9 109 3,14 1 10 6 (2 - 2 ) 165мкДж
26.
7. Заряженная частица, пройдя ускоряющую разность потенциаловU=600 кВ, приобрела скорость = 5,4 106 м/с. Определить
удельный заряд частицы (отношение заряда к массе).
Дано:
Си:
U=600 кВ 6 105 В
= 5,4 106 м/с
Найти:
q/m.
Решение:
A12 q ( 1 - 2 ) q U
2
mυ
A12
2
2
mυ0
mυ
2
2
υ0 0м/с
mυ 2
qU
2
2
27.
mυqU
2
2
2
q υ
m 2U
6 2
q (5,4 10 )
24,3МКл/кг
5
m
2 6 10
28.
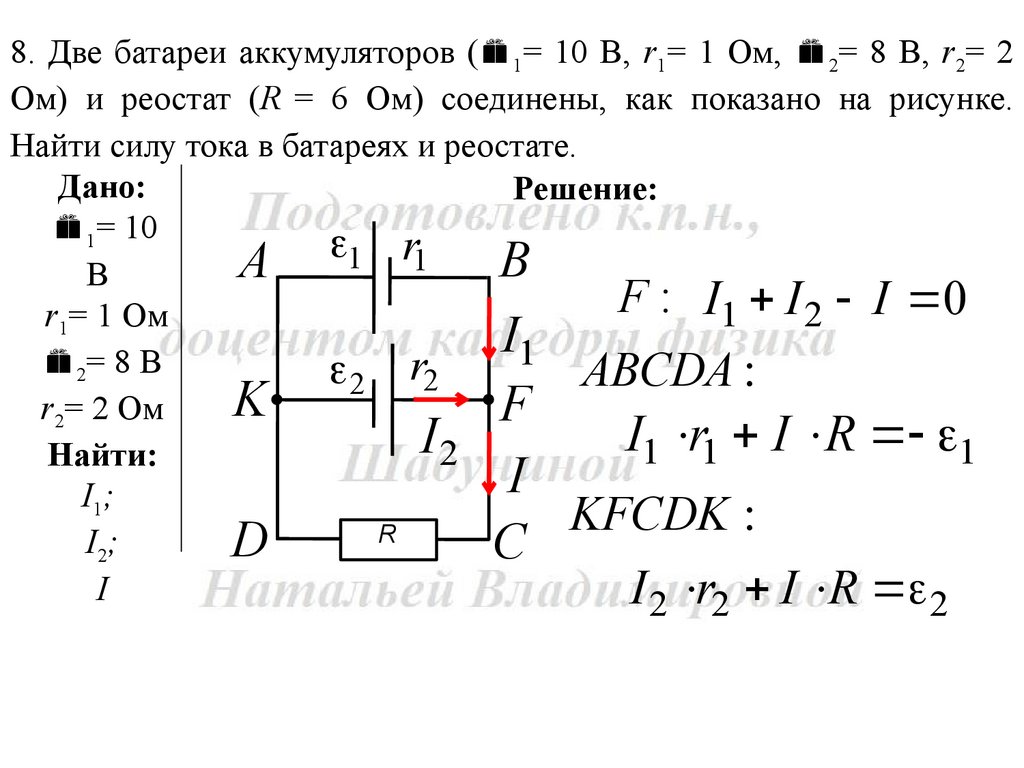
8. Две батареи аккумуляторов ( 1= 10 В, r1= 1 Ом, 2= 8 В, r2= 2Ом) и реостат (R = 6 Ом) соединены, как показано на рисунке.
Найти силу тока в батареях и реостате.
Дано:
Решение:
1= 10
1 r1
В
А
В
F : I1 I 2 I 0
r1= 1 Ом
I
1
2= 8 В
2 r2
ABCDA :
K
r2= 2 Ом
F
I1 r1 I R 1
I2
Найти:
I
I1 ;
KFCDK
:
R
I2;
D
С
I
I 2 r2 I R 2
29.
I1 I 2 I 0I1 r1 I R 1
I 2 r2 I R 2
I1 I 2 I 0
I1 6 I 10
2 I 2 6 I 8
I1 I 2 I 0
I1 10 6 I
I 2 4 3I
30.
I1 I 2 I 0I1 10 6 I
I 2 4 3I
10 6 I 4 3I I 0
10 I 6
II1 -6,4A
0,6A
I 2 5,8A
I1 10 6 (-0,6) -6,4A
I 2 4 3 (-0,6) 5,8A
31.
9. Сила тока в проводнике сопротивлением R = 100 Ом равномернонарастает от I0= 0 А до Imax= 10 А в течении времени = 30 с.
Определить количество теплоты Q, выделившееся за это время в
проводнике.
Дано:
Решение:
R = 100 Ом
I
I I 0 kt
I0= 0 А
Imax
Imax= 10 А
I max
t = 30 с
k
Найти:
t
Q.
0
1
I t
3
1 2
Q dQ I R dt t R dt
9
2
32.
33
1 2
R 2
R
R
Q t R dt t dt
9
90
9 3
27
3 R
Q
27
3
30 100
Q
100кДж
27
33.
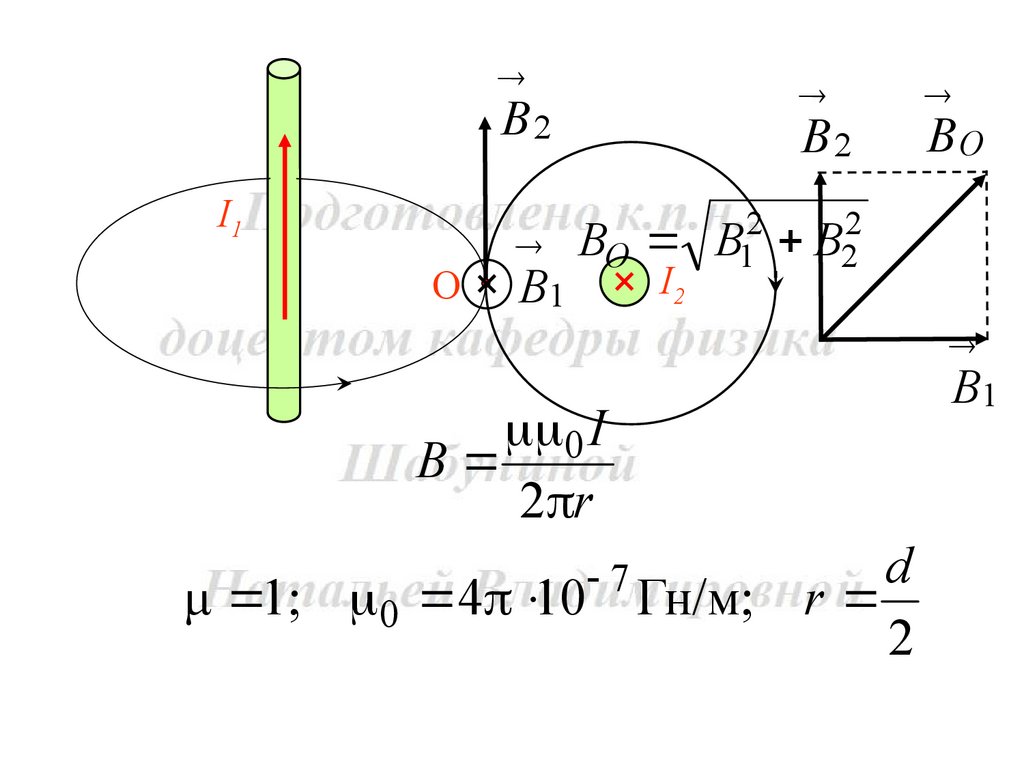
10. Два бесконечно длинных прямых провода скрещены подпрямым углом. По проводам текут токи I1= 80 А и I2= 60 А.
Расстояние между проводами равно d = 10 см. Определить
магнитную индукцию в точке О, одинаково удалённой от обоих
проводников.
Решение:
Дано:
Си:
I1= 80 А
I2= 60 А
В О В1 В 2
d = 10 см 0,10 см
Найти:
В.
34.
В2I1
О
В1
В2
ВО
ВО В12 В22
I2
0 I
B
2 r
d
μ 1; 0 4 10 Гн/м; r
2
7
В1
35.
0 I1B1
d
ВО
0 I 2
B2
d
2
В1
2
В2
0
ВО
I12 I 22
d
7
4 10
ВО
0,10
2
2
80 60 400мкТл
36.
11. Прямой провод длиной l = 10 см, по которому течет ток I = 20 А,находится в однородном магнитном поле с индукцией В = 0,01 Тл.
Найти угол между направлениями вектора магнитной индукции и
тока, если на провод действует сила F= 10-2Н.
Дано:
l = 10 см
I = 20 А
В = 0,01 Тл
F= 10-2Н
Найти:
.
Си:
0,10 м
Решение:
FА I B sin
В
I
F
A
FА
arcsin
I B
37.
FАarcsin
I B
10 2
arcsin
30
20 0 ,10 0,01
38.
12. Проволочный виток радиусом R = 5 см находится в однородноммагнитном поле напряженностью H = 2кА/м. Плоскость витка образует угол = 60 с направлением поля. По витку течет ток I = 4 А.
Найти механический момент M, действующий на виток.
Дано:
Си:
Решение:
R = 5 см
0,05 м
pm
H
3
H = 2кА/м 2 10 А/м
a = 60
I=4А
Найти:
M
M.
I
M pm B sin
pm N I S
S R
2
B 0 H
39.
2M N I R 0 H sin
2
M 4 3,14 0,05 4 3,14 10
7
3
2 10 sin30 39,4мкН м
40.
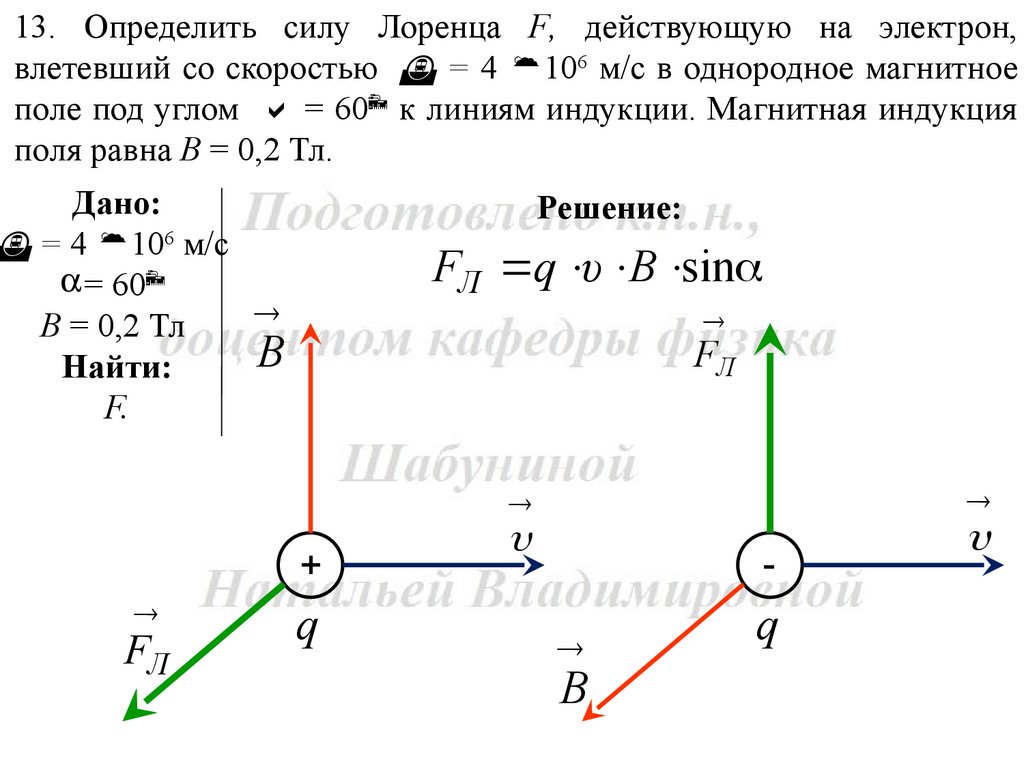
13. Определить силу Лоренца F, действующую на электрон,влетевший со скоростью = 4 106 м/с в однородное магнитное
поле под углом = 60 к линиям индукции. Магнитная индукция
поля равна В = 0,2 Тл.
Дано:
= 4 106 м/с
a = 60
В = 0,2 Тл
В
Найти:
F.
Решение:
FЛ q υ B sin
FЛ
+
FЛ
q
В
q
41.
FЛ q υ B sinFЛ 1,6 10 19 4 106 0,2 sin30 6,4 10 14 64фН
42.
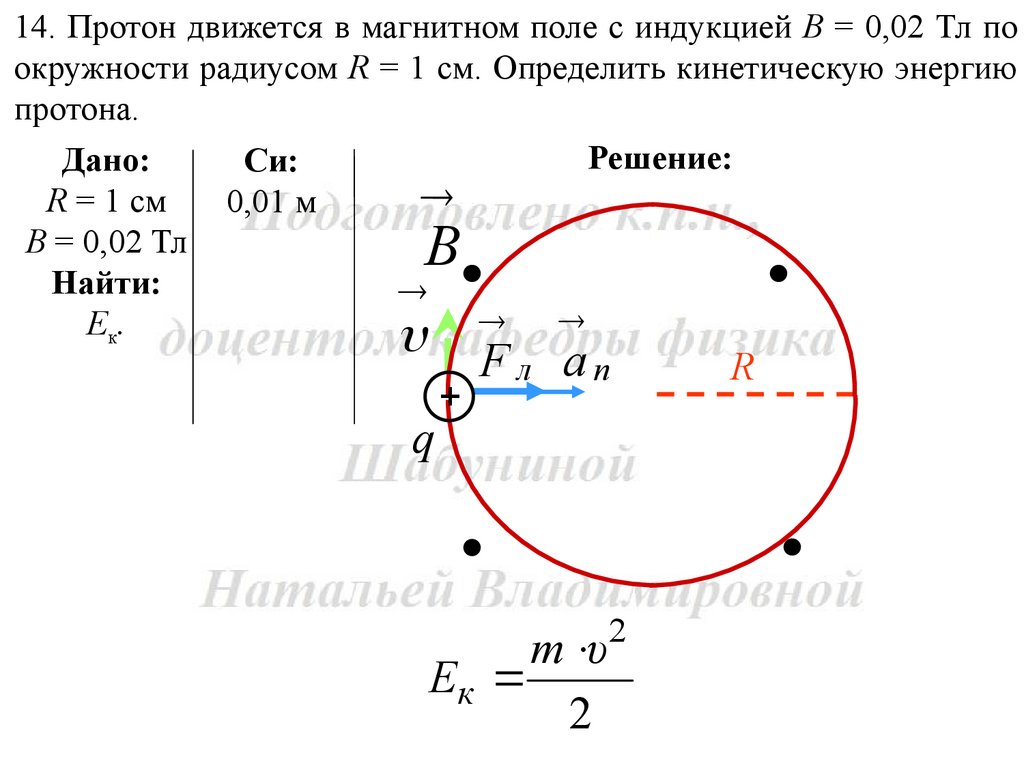
14. Протон движется в магнитном поле с индукцией В = 0,02 Тл поокружности радиусом R = 1 см. Определить кинетическую энергию
протона.
Решение:
Дано:
Си:
R = 1 см
0,01 м
В = 0,02 Тл
Найти:
Ек.
F а
R
л
n
В
q
+
m υ
Eк
2
2
43.
FЛ q υ B sinFЛ q B
FЛ m an
2
q B m
R
q B R
υ
m
2
2
m υ m(q B R)
(q B R )
Eк
2
2m
2m 2
2
44.
(q B R )Eк
2m
Eк
(1,6 10
19
2
0 ,02 0 ,01)
2 1,67 10 27
2
3 10
19
Дж
45.
15. Плоский контур, площадь которого равна S = 300 см2, находитсяв однородном магнитном поле с индукцией В = 0,01 Тл. Плоскость
контура перпендикулярна линиям индукции. В контуре
поддерживается неизменный ток I = 10 А. Определить работу А
внешних сил по перемещению контура с током в область
пространства, магнитное поле в которой отсутствует.
Дано:
Си:
Решение:
S = 300 см2 3 10-2 м2
B1
В1 = 0,01 Тл
В2 = 0 Тл
I = 10 А
Найти:
А.
I
Aвнешних сил Aмагнитного поля
46.
Aмагн. поля I (Ф2 - Ф1)Aвн. сил I (Ф1 - Ф2 )
Ф B S cos
B1
n
Ф1 B1 S
Ф 2 0Вб
I
Aвн. сил I B1 S
Aвн. сил 10 0,01 3 10
2
3мДж



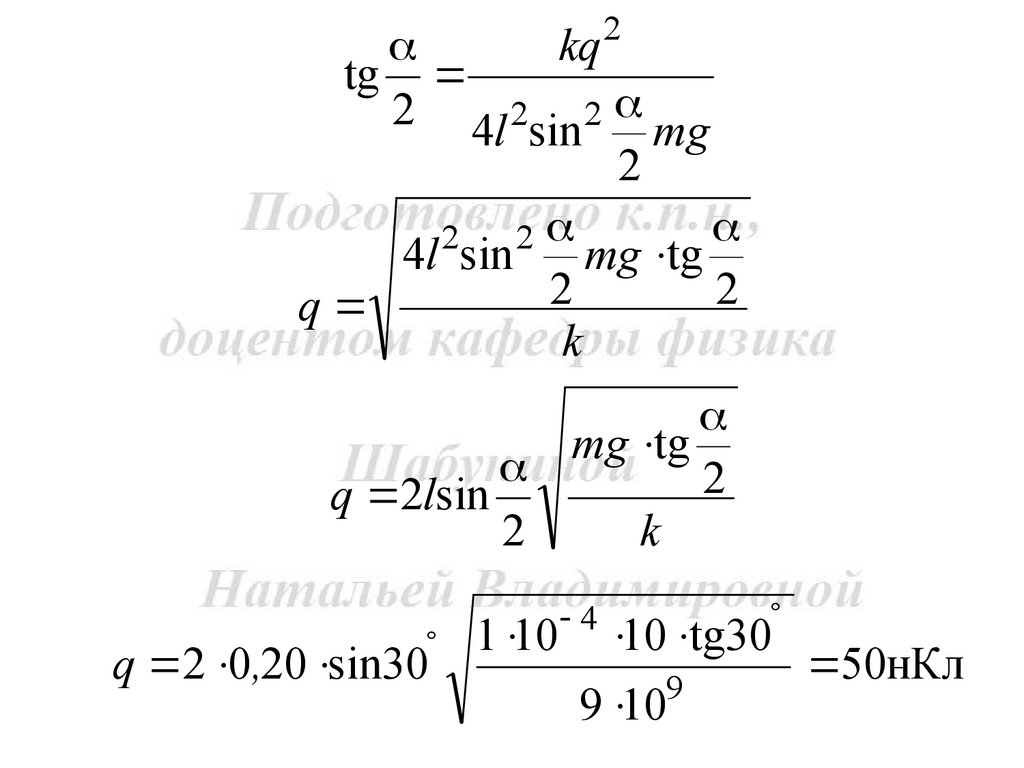









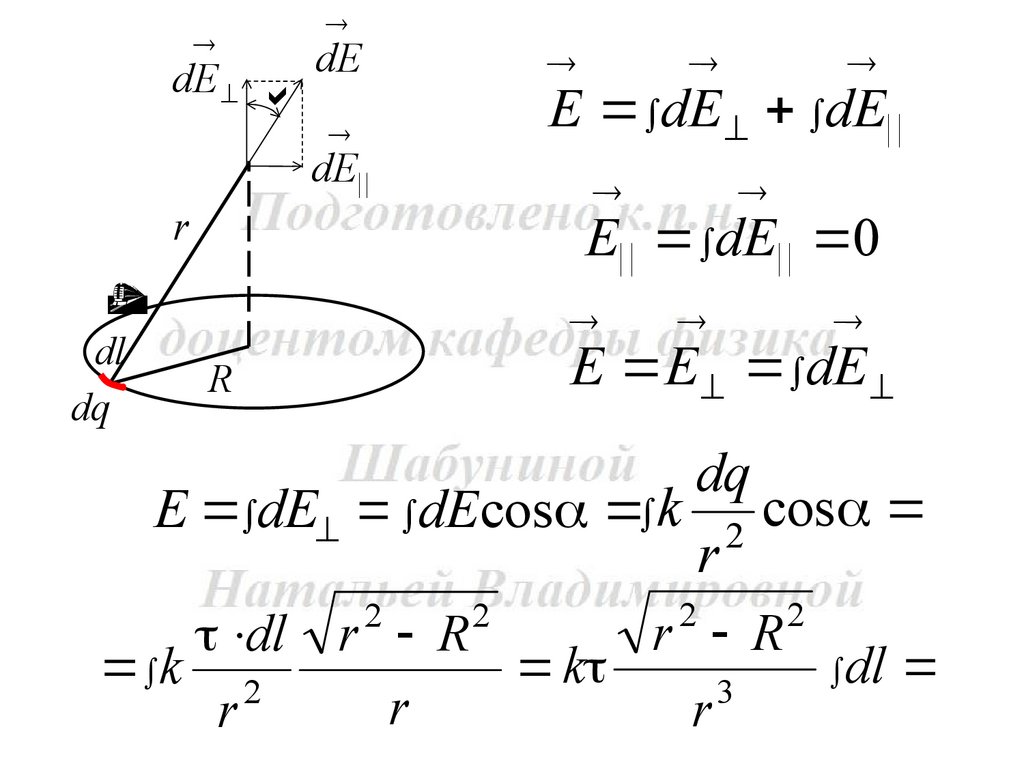










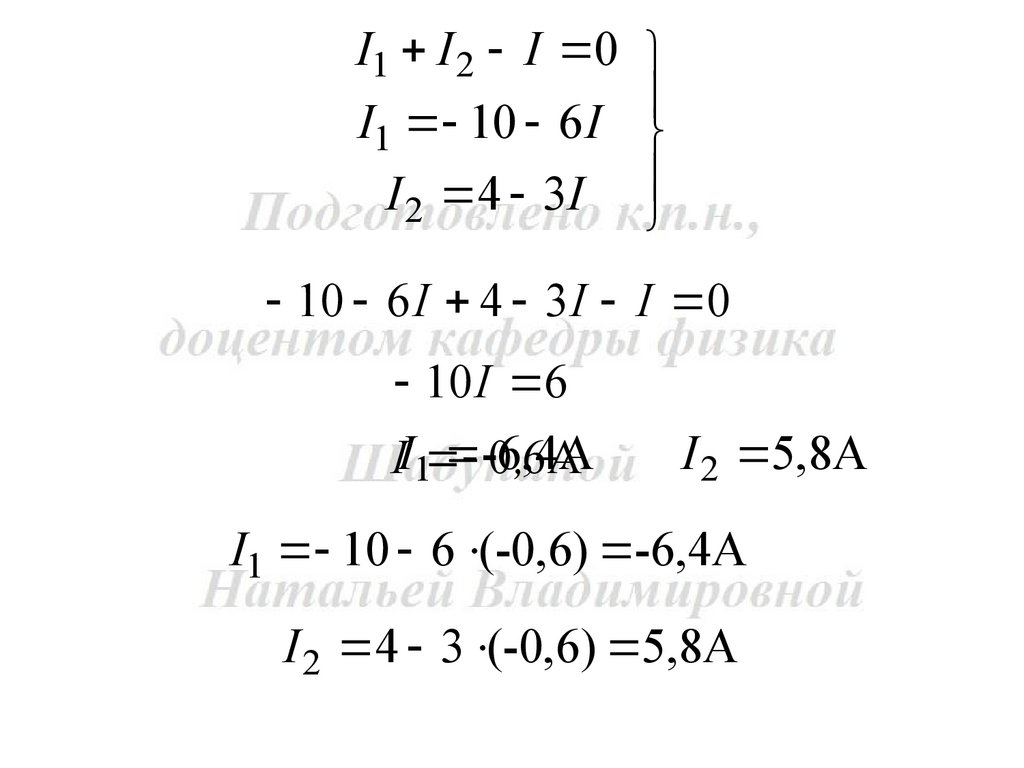









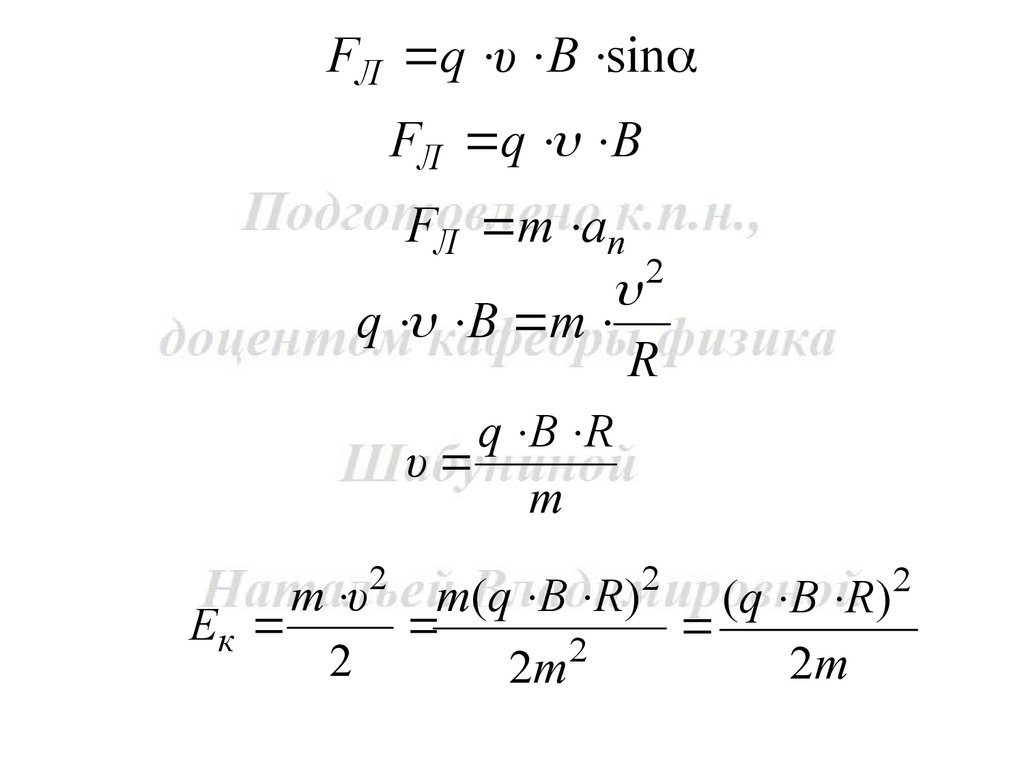



 physics
physics








