Сложные колебания пружинного маятника

1.

«Сложные колебания пружинного
маятника»
Научно-исследовательская работа
ВЫПОЛНИЛИ:
МАКСИМОВА Е.Ю.
ВЕЛИКАНОВ В.А.
РУКОВОДИТЕЛЬ:
УЧИТЕЛЬ ФИЗИКИ ШКОЛЫ№1293:
БРАЖНИКОВ М.А.,

2.

Непредвиденные колебания
в природе и технике
Мост «Такома-Нэрроуз» (1940)
Танцующий мост в Волгограде

3.

Пружинный маятник и реальные
колебательные системы
“Колебания шпренгельных
систем с составной балкой
жёсткости”
В.В. Егоров, П.Н. Григорьев
опубликовано в ж. Изв. Петерб.
Унив. Путей Сообщения, 2008 г.
Возникновение флаттера при
набегании воздушного потока на
крыло самолёта,
по М.В. Келдышу, 1940-е гг.
Пешеходный мостик, ГУМ
Тема учебно-исследовательской работы – актуальна!

4.

Модели пружинного маятника
1) Модель: тело – материальная
точка на невесомой упругой
пружине
2) Модель: тело – материальная
точка на весомой упругой
пружине
Цель: определить применимость
моделей к описанию колебаний и
расчёту периода колебаний
М

5.

Цели и задачи исследования
Цель (первоначальная):
определить применимость моделей 1 и 2 к описанию колебаний и
расчёту периода колебаний пружинного маятника
Цель (уточнённая):
определить условия возбуждения колебательных мод вертикального
пружинного маятника.
Задачи:
Экспериментальное определение коэффициента жёсткости пружины;
Экспериментальное определение периода колебаний пружинного маятника.
Сравнение экспериментальных и теоретических данных;
Экспериментальное исследование условий возбуждения и характеристик
крутильных колебаний пружинного маятника.

6.

Задачи исследования
Экспериментальное определение
коэффициента жёсткости пружины;
Экспериментальное определение
периода колебаний пружинного
маятника. Сравнение
экспериментальных и теоретических
данных;
Экспериментальное исследование
условий возбуждения и
характеристик крутильных
колебаний пружинного маятника.
Фото экспериментальной установки

7.

Параметры исследуемых пружин
Цилиндрические пружины закрытой навивки:
I – mI = 44, 24 г, l0I = 11,4 см, dI = 23 мм;
II – mII = 45,73 г, l0II = 11,2 см, dII = 25,5 мм
III – mIII = 52,88 г, l0III = 10,7 см, dIII = 25,мм
Масса – электронные весы с точностью до 0,005 г
Длина – металлическая линейкой (цена деления 1 мм)
Диаметр – штангенциркуль (с точностью до 0,05 мм)

8.

Определения коэффициента жесткости
2,5
0,7
0,6
2
0,5
1,5
0,4
Сила
упругости,
Н
Сила
упругости,
Н
1
0,3
0,2
0,5
0,1
0
0
0
0,2
0,4
0,6
Растяжение пружины, м
0,8
1
0
0,2
0,4
0,6
0,8
Растяжение пружины, м
1

9.

Сравнение экспериментальных и теоретических данных
(Графики зависимости периода колебаний от массы)
2,1
2
1,9
1,8
1,7
1,6
1,5
Период
1,4
колебаний, с
Весомая
Эскперимент
Т, с
Реальный
подсчет
Весомая
1,3
Невесомая
пружина
Невесомая
1,2
1,1
0,9
1
0,8
0,05
0,7
0,15
Масса грузов, кг
0,25
0,1
0,3
0,5
m, кг
0,7

10.

Выводы
Формула периода (2) точнее описывает период колебаний
вертикального пружинного маятника в зависимости от массы
груза.
Экспериментально установлены условия возбуждения
крутильных колебаний:
● пружина I Mкр = 100 г;
● пружина II Mкр = 150 г;
● пружина III Mкр = 300 г.

11.

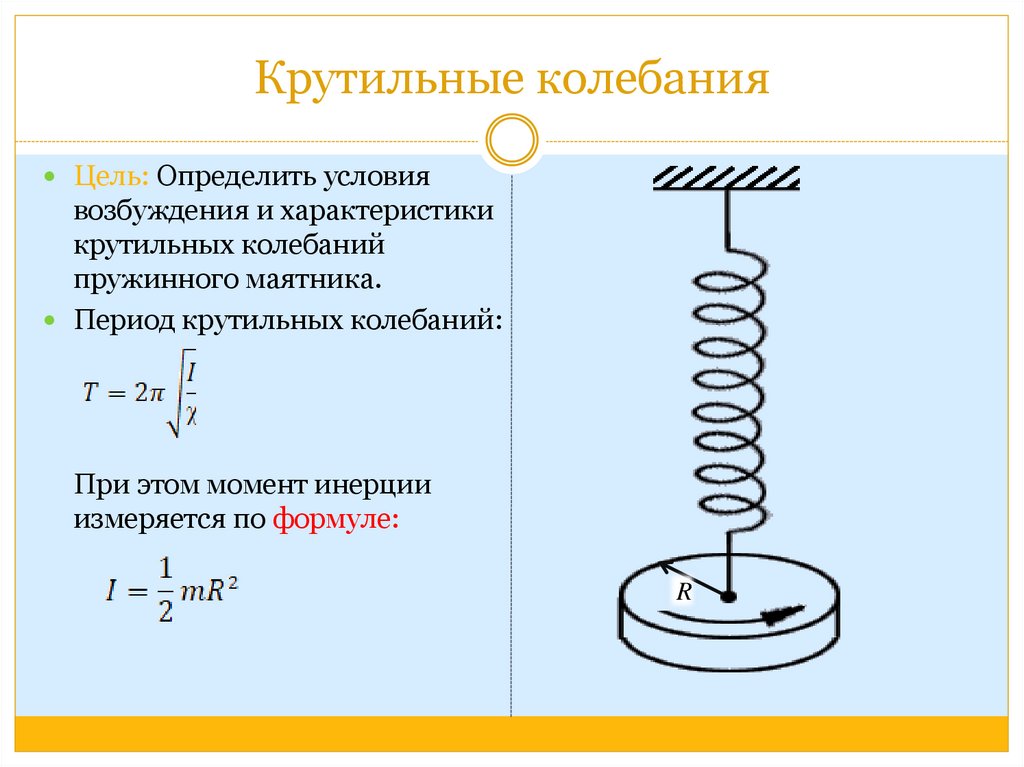
Крутильные колебания
Цель: Определить условия
возбуждения и характеристики
крутильных колебаний
пружинного маятника.
Период крутильных колебаний:
При этом момент инерции
измеряется по формуле:
R

12.

Результаты
0,023
0,032
0,023
0,045
1,428
1,654
• При массе груза близкой к
критической крутильные
колебания происходят чаще
• Пружина проворачивается на
больший угол, при большем
диаметре груза.
1,415
Пружина I
1,609
Пружина II
• Колебания с грузом большего
диаметра медленнее затухают.

13.

Крутильные и возвратно-поступательные колебания
вертикального пружинного маятника, по А. Зоммерфельду
Q – осевая сила
P – тангенсальная сила
G – модуль сдвига,
r – радиус пружины,
Jp – геометрический полярный момент
инерции (для сплошного диска
½πr2),
l – длина проволоки пружины,
- коэффициент Пуассона

14.

Выводы
Предварительное сравнение экспериментов с теорией
показывает, что:
в ряде случаев наблюдаются «биения», когда крутильные
колебания, то усиливаются по амплитуде, то ослабевают,
что объясняется по модели А. Зоммерфельда близостью
частот крутильных и вертикальных колебаний
не ясно, как следует из модели, предложенной
А. Зоммерфельдом, наличие “порогового” значения массы
груза для возбуждения крутильных колебаний
наблюдаемые при больших растяжениях колебания в
виде стоячих волн не предсказываются моделью
Зоммерфельдом