Проверка статистических гипотез. Статистическая функция распределения случайной величины

1.

Дисциплина: «Основы научных исследований»
Лабораторная работа № 2
Проверка статистических гипотез.
УЧЕБНЫЕ ВОПРОСЫ:
1. Статистическая функция
распределения случайной
величины.
2. Точечные оценки параметров
функции распределения
случайной величины.
3. Построение доверительного
интервала для параметров
нормального распределения.
4.Проверка статистических гипотез
Рекомендуемая литература:
1

2.

Учебный вопрос №1 Статистическая функция распределения
случайной величины.
2

3.

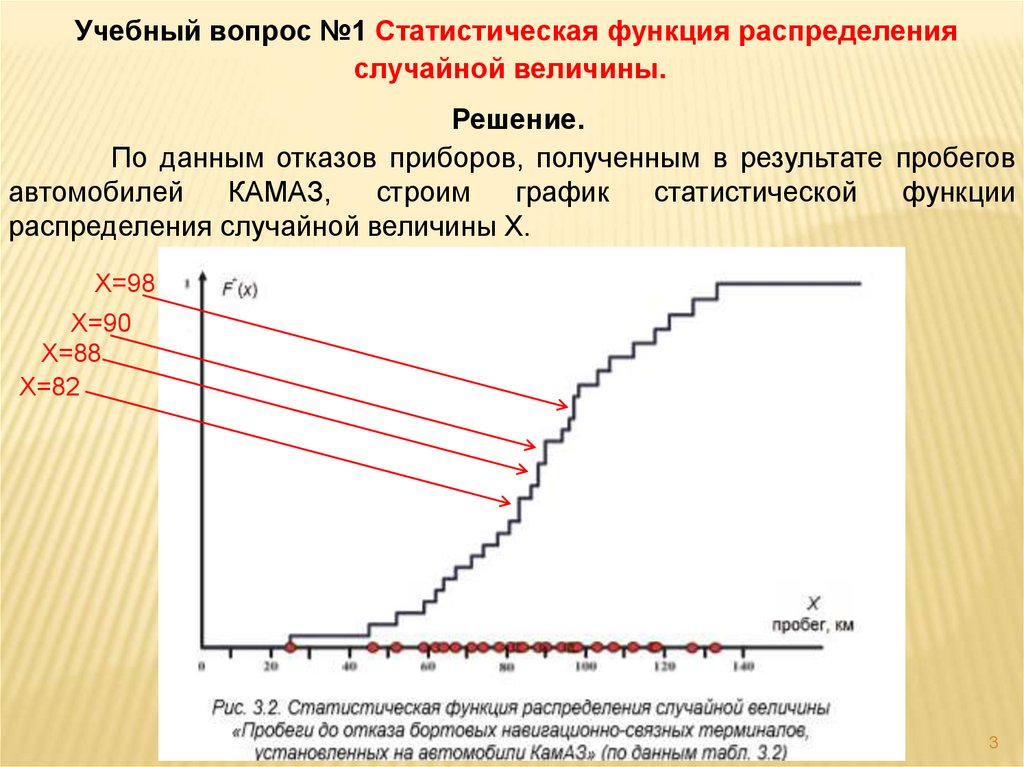
Учебный вопрос №1 Статистическая функция распределения
случайной величины.
Решение.
По данным отказов приборов, полученным в результате пробегов
автомобилей
КАМАЗ,
строим
график
статистической
функции
распределения случайной величины Х.
Х=98
Х=90
Х=88
Х=82
3

4.

Учебный вопрос №2 Точечные оценки параметров
функции распределения случайной величины.
2.1 Основные определения.
4

5.

2.2 Нахождение точечной оценки математического ожидания
случайной величины по данным выборки.
5

6.

2.3 Нахождение точечной оценки дисперсии, среднего квадратичного
отклонения и коэффициента вариации случайной величины
по данным выборки
Точечная оценка дисперсии определяется по формуле:
6

7.

7

8.

Для нормально распределенной случайной величины значение
коэффициента вариации V должно быть меньше 0,3. Исходя из этого,
гипотеза о нормальном законе распределения для случайной величины
(пробеги автомобилей КАМАЗ до отказа прибора), правдоподобна.
8

9.

Учебный вопрос №3 Построение доверительного интервала
для параметров нормального распределения.
3.1 Основные определения.
9

10.

10

11.

11

12.

3.2 Пример построения доверительного интервала.
12

13.

13

14.

14

15.

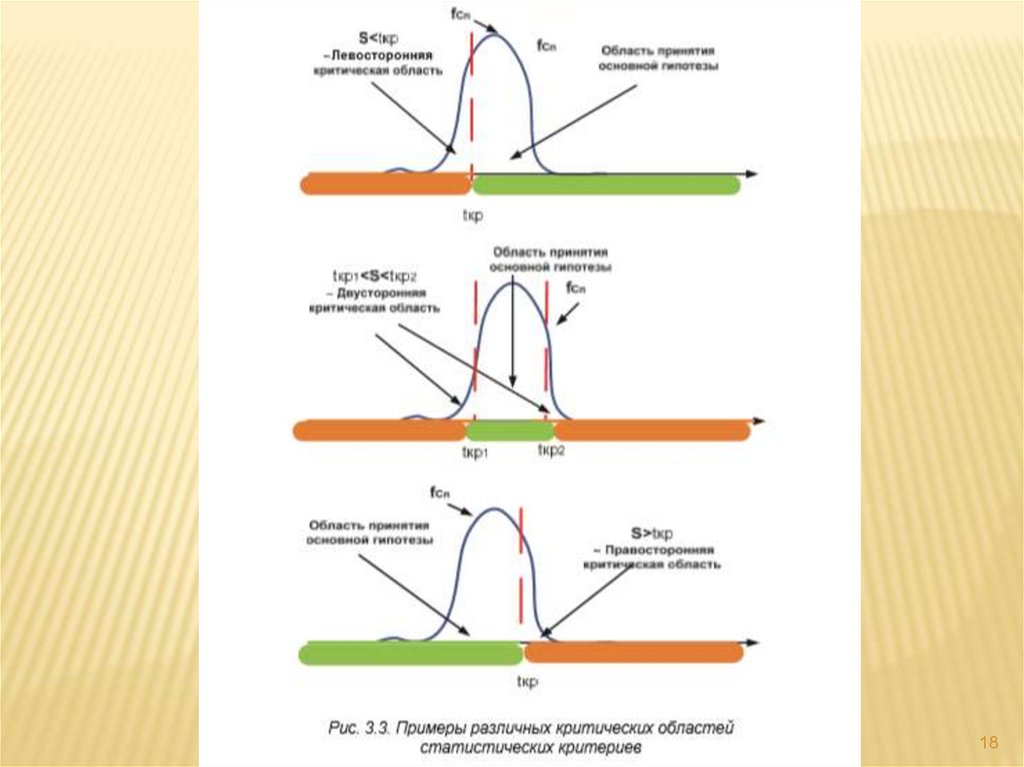
Учебный вопрос №4 Проверка статистических гипотез
4.1 Основные понятия.
15

16.

16

17.

17

18.

18

19.

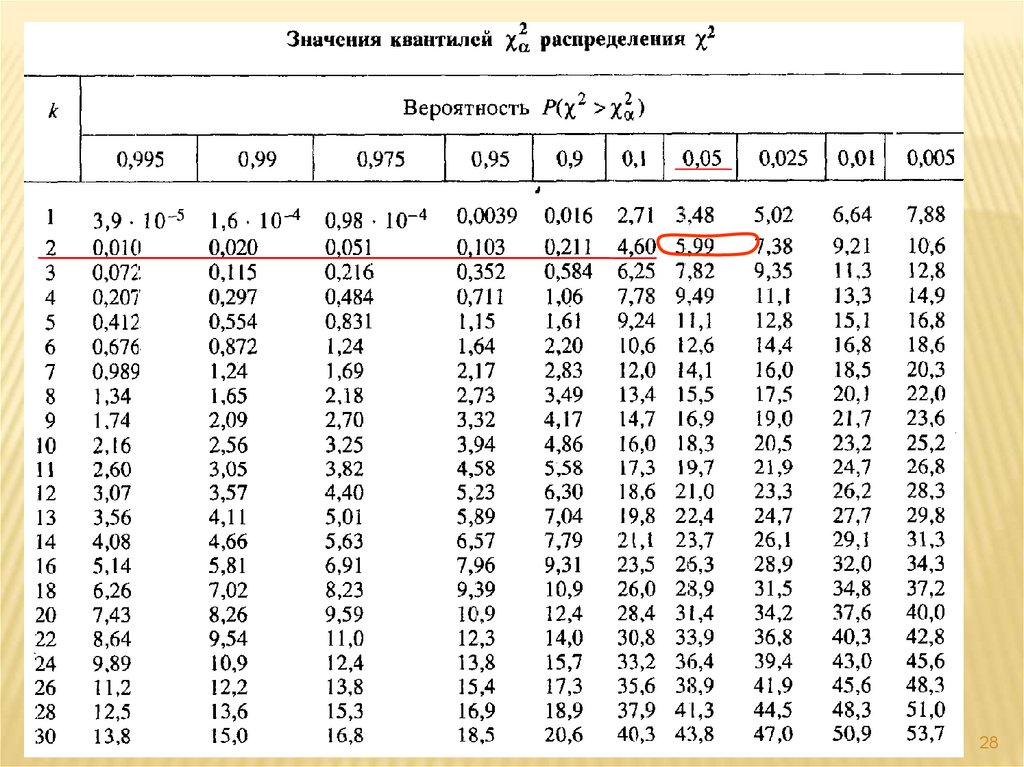
4.2 Проверка гипотез о законе распределения с использованием
критерия Пирсона χ2
19

20.

20

21.

21

22.

4.3 Пример проверки гипотеза о законе распределения
22

23.

23

24.

В соответствии с требованиями критерия Пирсона χ2, перегруппируем
данные так, чтобы в каждом интервале было не менее пяти значений.
24

25.

25

26.

26

27.

где из условия примера n=40.
27

28.

28