Similar presentations:
Проверка статистических гипотез о законе распределения
1. Проверка статистических гипотез о законе распределения
2. Выравнивание статистических рядов
Вовсяком
статистическом
распределении
неизбежно присутствуют элементы случайности,
связанные с тем, что число наблюдений
ограничено, что произведены именно те, а не
другие опыты, давшие именно те, а не другие
результаты.
Только при очень большом числе наблюдений эти
элементы случайности сглаживаются, и случайное
явление
обнаруживает
присущую
ему
закономерность.
3. Выравнивание статистических рядов
На практике обычно не имеем дела с такимбольшим числом наблюдений и считаем, что
любому
статистическому
распределению
свойственны в большей или меньшей или меньшей
степени черты случайности.
При обработке статистического материала часто
приходится решать вопрос о том, как подобрать
для данного статистического ряда теоретическую
кривую распределения, выражающую лишь
существенные черты статистического материала.
Такая задача называется задачей выравнивания
статистических рядов.
4. Выравнивание статистических рядов
Задача выравнивания заключается в том, чтобыподобрать плавную кривую распределения, с той
или иной точки зрения наилучшим образом
описывающую
данное
статистическое
распределение.
Вид теоретической кривой выбирается заранее из
соображений, связанных с существом задачи, а в
некоторых случаях просто с внешним видом
статистического распределения.
5. Выравнивание статистических рядов
Аналитическое выражение выбранной кривойраспределения зависит от некоторых параметров.
Задача выравнивания статистического ряда
переходит в задачу рационального выбора тех
значений параметров, при которых соответствие
между
статистическим
и
теоретическим
распределениями оказывается наилучшим.
6. Выравнивание статистических рядов
Требуется подобрать параметры так, чтобыфункция наилучшим образом описывала данный
статистический материал.
Один из методов - метод моментов. Согласно
методу моментов, параметры выбираются с таким
расчетом,
чтобы
несколько
важнейших
характеристик
(моментов)
теоретического
распределения были равны соответствующим
статистическим характеристикам.
7. Выравнивание статистического ряда
Пусть данное статистическое распределениевыровнено с помощью некоторой теоретической
кривой . Как бы хорошо ни была подобрана
теоретическая кривая, между нею и статистическим
распределением
неизбежны
некоторые
расхождения.
8. Выравнивание статистического ряда
Возникает вопрос: объясняются ли эти расхождениятолько случайными обстоятельствами, связанными
с ограниченным числом наблюдений, или они
являются существенными и связаны с тем, что
подобранная нами кривая плохо выравнивает
данное статистическое распределение. Для ответа
на этот вопрос служат «критерии согласия».
9. Критерии согласия
Критериями согласия называются критерии дляпроверки гипотез о виде закона распределения
случайной величины.
10. Критерии согласия
На основании данного статистического материаланам предстоит проверить гипотезу , состоящую в
том, что случайная
подчиняется некоторому
определенному закону распределения.
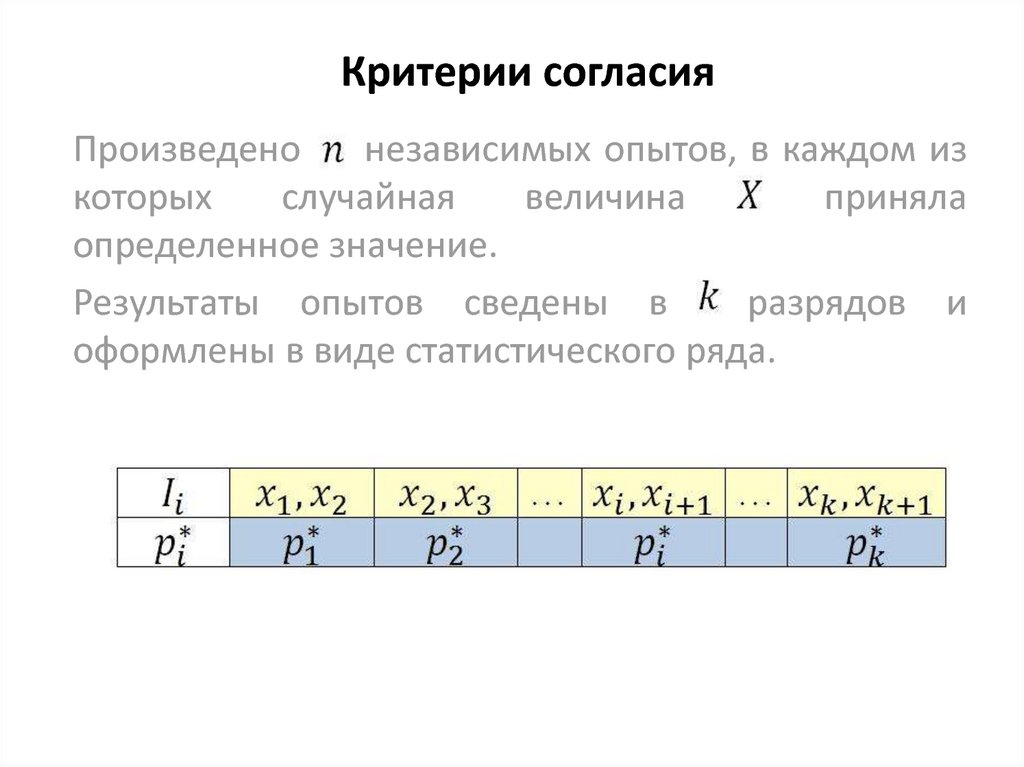
11. Критерии согласия
Произведенонезависимых опытов, в каждом из
которых
случайная
величина
приняла
определенное значение.
Результаты опытов сведены в
разрядов и
оформлены в виде статистического ряда.
12. Критерии согласия
Требуетсяпроверить,
согласуются
ли
экспериментальные данные с гипотезой о том, что
случайная величина
имеет данный закон
распределения (теоретический).
Зная теоретический закон распределения, можно
найти теоретические вероятности попадания
случайной величины в каждый из разрядов:
13. Критерии Пирсона
Коэффициентывводятся потому, что в общем
случае отклонения, относящиеся к различным
разрядам, нельзя считать равноправными по
значимости. Действительно, одно и то же по
абсолютной величине
может быть мало
значительным, если сама вероятность
велика, и
очень заметным, если она мала. Поэтому
естественно
«весу»
взять
обратно
пропорциональными вероятностям разрядов
:
14. Критерии Пирсона
Проверяя согласованность теоретического истатистического распределения, будем исходить из
расхождений
между
теоретическими
вероятностями и наблюденными частотами . В
качестве меры расхождения между теоретическим
и
статистическим
распределениями
сумму
квадратов отклонений
, взятых с некоторыми
«весами»
:
15. Критерий Пирсона
Пирсон показал, что если положить, то при
больших
закон распределения величины
обладает простым свойством: он практически не
зависит от функции распределения и от числа
опытов , а зависит только от числа разрядов , а
именно, этот закон при увеличении приближается
к так называемому «распределению
».
16. Критерий Пирсона
При таком выбореимеет вид:
«весы» мера расхождения
17. Статистическая гипотеза
Распределениезависит от параметра
,
называемого
числом
«степеней
свободы»
распределения. Число «степеней свободы» равно
числу разрядов минус число независимых условий
(«связей»), наложенных на частоты :
18. Критерий Пирсона
Примеры:1.
требуем, чтобы сумма частот была равна
единице (это требование накладывается во всех
случаях);
2.
,
подбираем
теоретическое
распределение
с тем условием, чтобы
совпадали теоретическое и статистическое
средние значения.
3.
,
требуем
того,
совпадения
теоретической и статистической дисперсий и т.д.
19. Статистическая гипотеза
Для распределениясоставлены специальные
таблицы. Пользуясь этими таблицами, можно для
каждого значения и числа степеней свободы найти
вероятность того, что величина, распределена по
закону , превзойдет это значение.
Распределение дает возможность оценить степень
согласованности теоретического и статистического
распределений.
20. Вычисление теоретических вероятностей нормального закона распределения
Пользуясь теоретическим нормальным закономраспределения с параметрами
,
находим вероятности попадания в разряды по
формуле
где
,
- границы -го разряда.
21. Вычисление теоретических вероятностей нормального закона распределения
ПримерВычислить вероятность попадания
интервал (-4; -3). Закон нормальный
математическим ожиданием
среднее квадратическое отклонение
в
с
,
.
22. Вычисление теоретических вероятностей нормального закона распределения
ПримерВычислить вероятность попадания в
интервал (-4; -3).
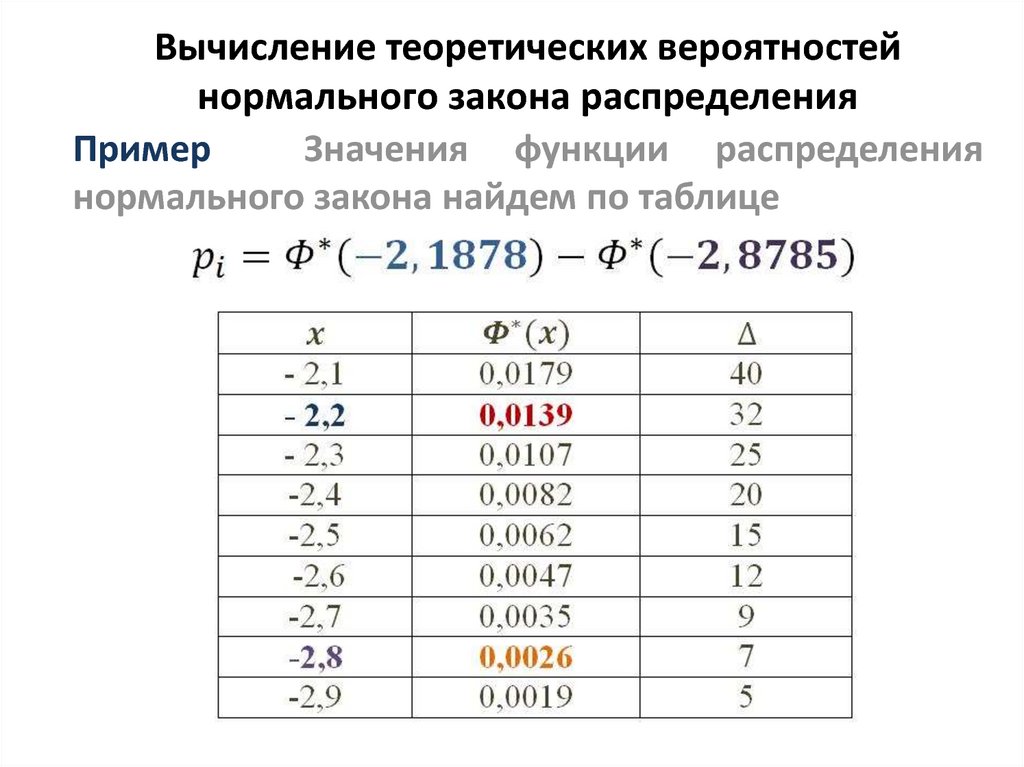
23. Вычисление теоретических вероятностей нормального закона распределения
ПримерЗначения функции распределения
нормального закона найдем по таблице
24. Вычисление теоретических вероятностей нормального закона распределения
ПримерЗначения функции распределения
нормального закона найдем по таблице
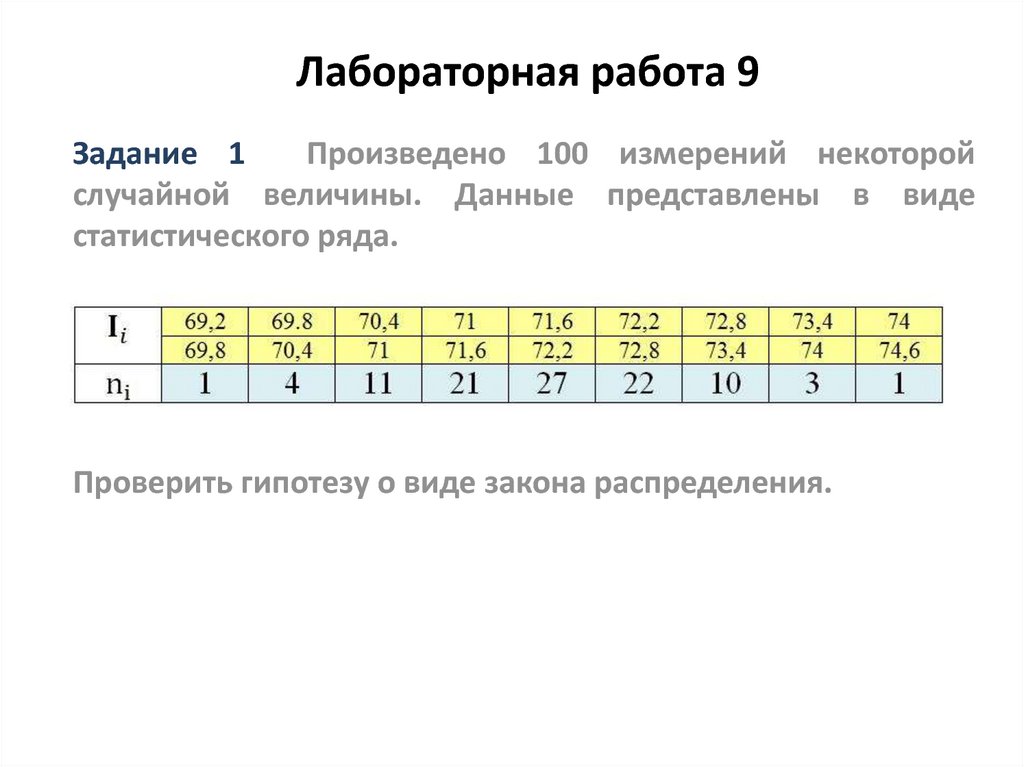
25. Лабораторная работа 9
Задание 1Произведено 100 измерений некоторой
случайной величины. Данные представлены в виде
статистического ряда.
Проверить гипотезу о виде закона распределения.
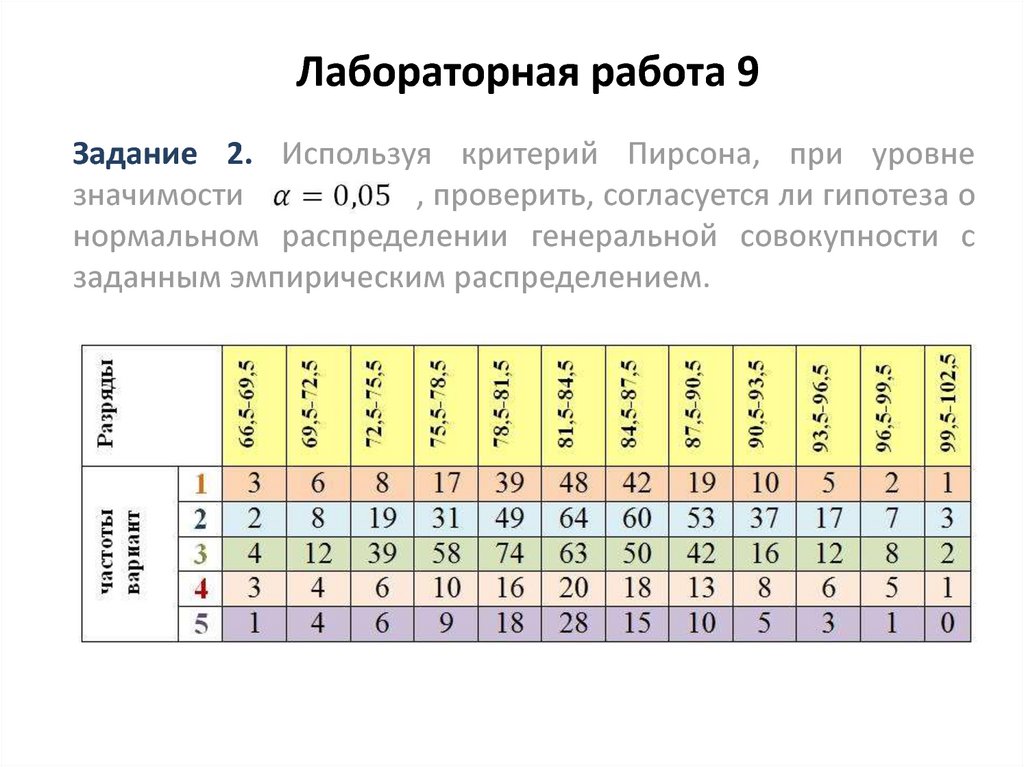
26. Лабораторная работа 9
Задание 2. Используя критерий Пирсона, при уровнезначимости
, проверить, согласуется ли гипотеза о
нормальном распределении генеральной совокупности с
заданным эмпирическим распределением.
27. Указание по выполнению лабораторной работы
1. Построить гистограмму.2. Выдвинуть нулевую гипотезу о том, что изучаемая
величина подчиняется … закону.
3. Найти выборочное среднее
и , исправленную
дисперсию
.
4. Вычислить
.
5. Задать уровень значимости (
).
6. Определить критическую область и проверить
выполнимость гипотезы.

























 mathematics
mathematics








