Ориентирование линий на местности. Прямая и обратная геодезические задачи

1.

Ориентирование

2.

ТЕМА: ОРИЕНТИРОВАНИЕ ЛИНИЙ НА
МЕСТНОСТИ. ПРЯМАЯ
И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ
ЗАДАЧИ.
Ориентированием линии называется
определение
ее
направления
на
местности относительно некоторого
направления, принятого за начальное.

3.

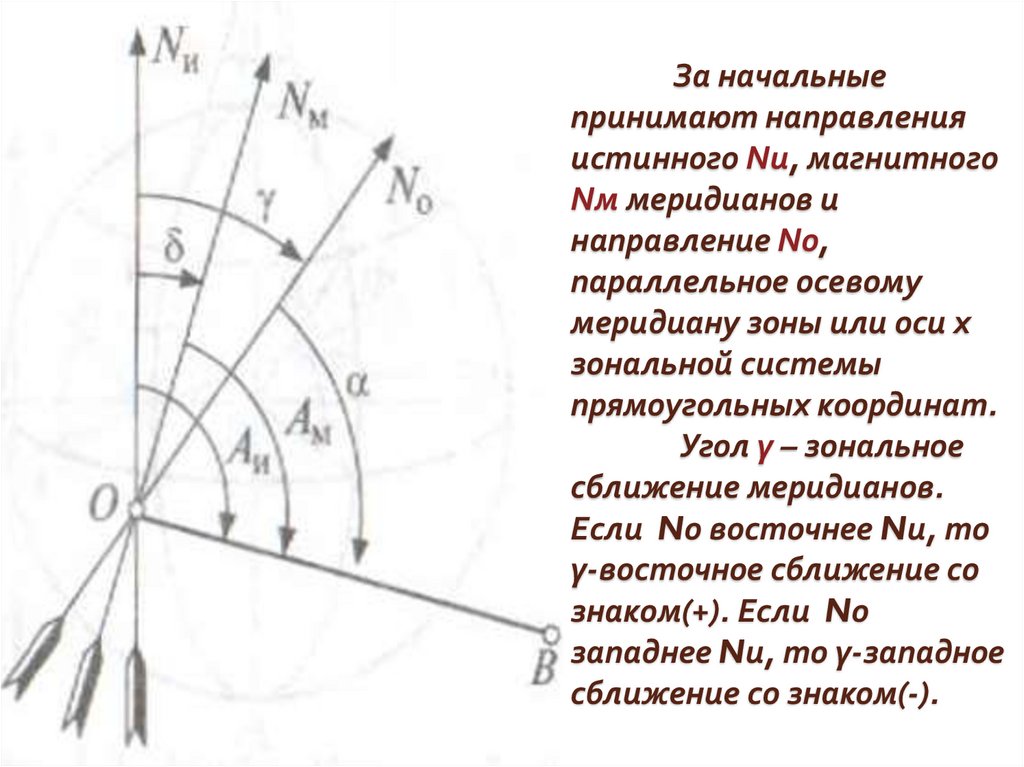
За начальные
принимают направления
истинного Nи, магнитного
Nм меридианов и
направление No,
параллельное осевому
меридиану зоны или оси х
зональной системы
прямоугольных координат.
Угол γ – зональное
сближение меридианов.
Если Nо восточнее Nи, то
γ-восточное сближение со
знаком(+). Если Nо
западнее Nи, то γ-западное
сближение со знаком(-).

4.

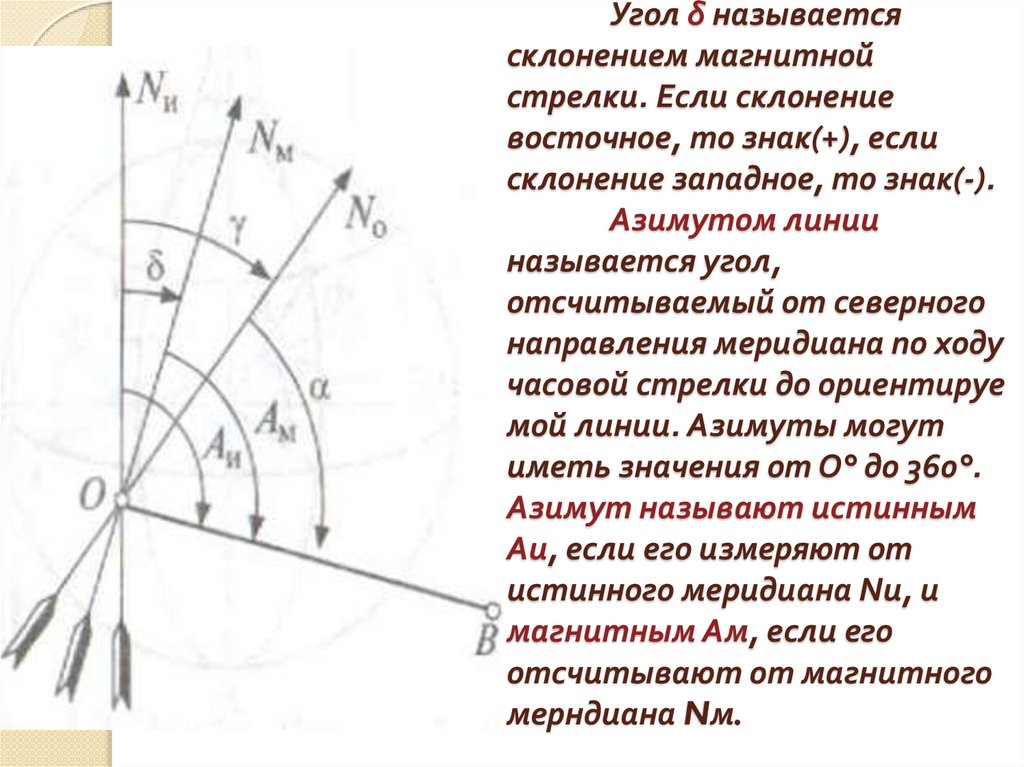
Угол δ называется
склонением магнитной
стрелки. Если склонение
восточное, то знак(+), если
склонение западное, то знак(-).
Азимутом линии
называется угол,
отсчитываемый от северного
направления меридиана по ходу
часовой стрелки до ориентируе
мой линии. Азимуты могут
иметь значения от О° до 360°.
Азимут называют истинным
Аи, если его измеряют от
истинного меридиана Nи, и
магнитным Aм, если его
отсчитывают от магнитного
мерндиана Nм.

5.

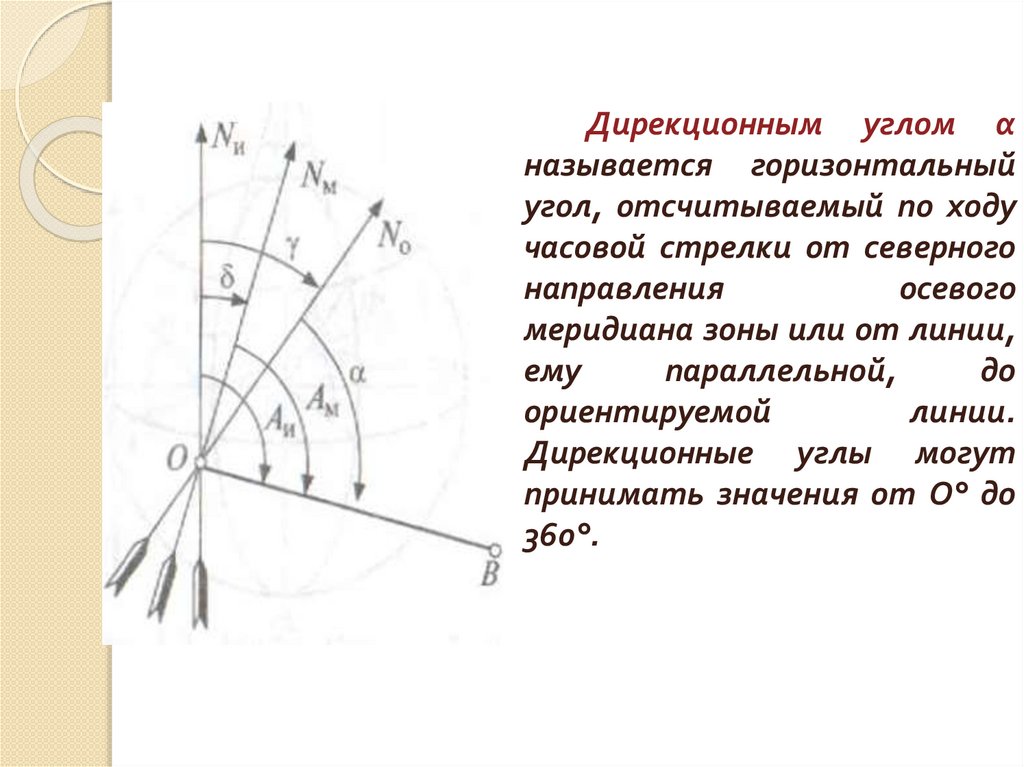
Дирекционным углом α
называется горизонтальный
угол, отсчитываемый по ходу
часовой стрелки от северного
направления
осевого
меридиана зоны или от линии,
ему
параллельной,
до
ориентируемой
линии.
Дирекционные углы могут
принимать значения от О° до
360°.

6.

Сближение меридианов
Пусть
lрасстояние
между
точками А и В, расположенными на
параллели с широтой φ. Проведя в
точках А и В касательные к
меридианам, проходящим через
эти точки, в пересечении получим
точку Т. Линии АТ и ВТ называются
полуденными, а угол γ между ними
– углом сближения меридианов, или
сближением меридианов, в точках
А и В.

7.

При небольшом значении угла γ расстояние l
можно принять за дугу радиуса ТА. Рассматривая
спектр АТВ и треугольник ОАТ, можно записать
γ = l /АТ,
АТ = Rtg(90° - φ°) = R/tgφ.
Следовательно
γ =( l /R)tgφ.
Выражая γ в минутах, получим
γ ´ =( l /R)tgφ*3438 ´.
При R=6371 км и l=1 км имеем
γ ´≈0,54tgφ.
Если известны долготы меридианов, проходящих через
точки А и В, то сближение определяем по формуле
γ ≈Δλsinφ,
где Δλ-разность долгот меридианов, проходящих через
точки А и В.

8.

Зависимости между дирекционным углом,
истинным и магнитным азимутами линии.
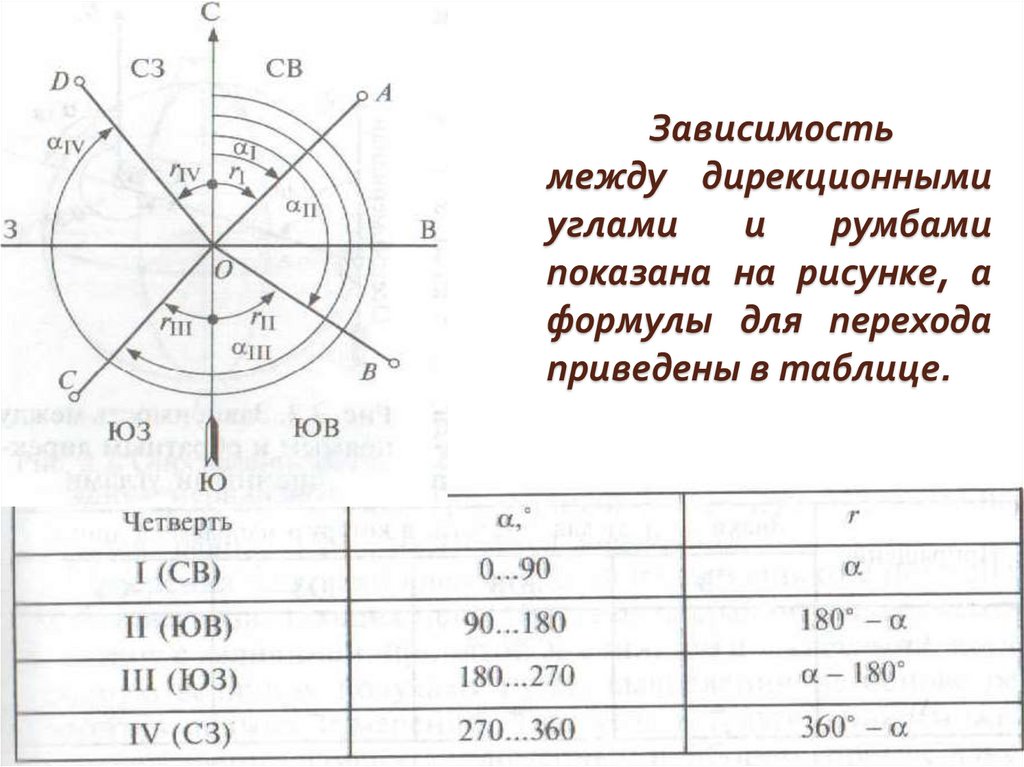
Зависимость между
истинным азимутом Аи
линии ОВ и дирекционным
углом α этой же линии.
Если No - параллель
осевому меридиану зоны,
а
γ-сближение
меридианов, то
Аи=α+γ

9.

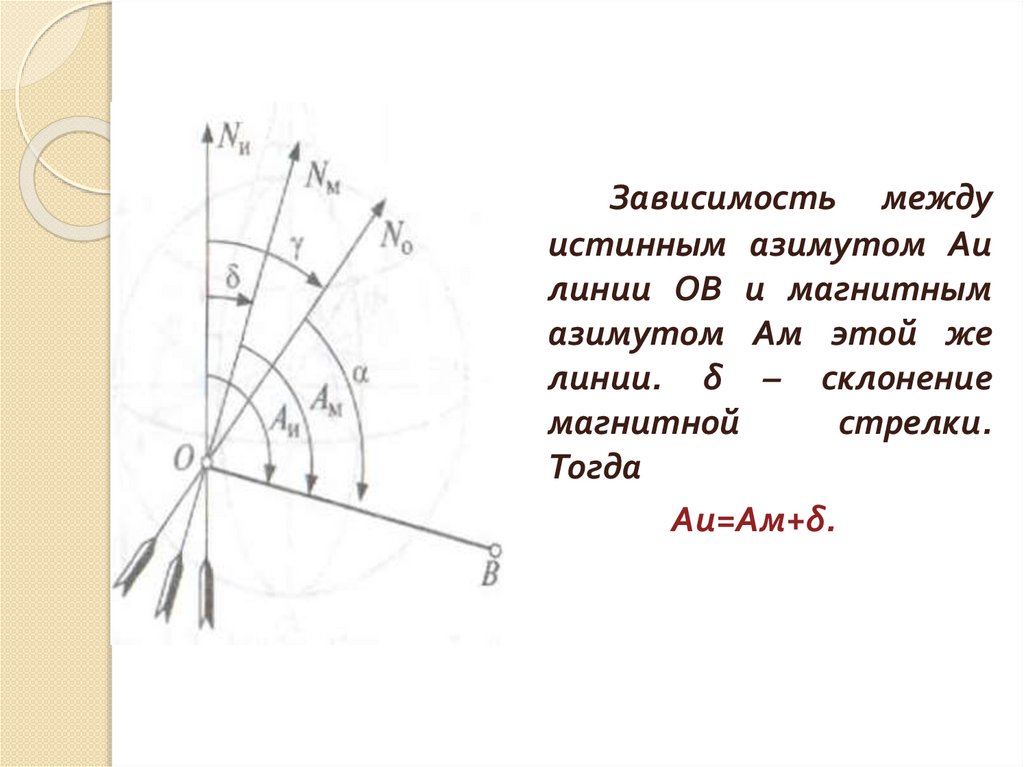
Зависимость между
истинным азимутом Аи
линии ОВ и магнитным
азимутом Ам этой же
линии. δ – склонение
магнитной
стрелки.
Тогда
Аи=Ам+δ.

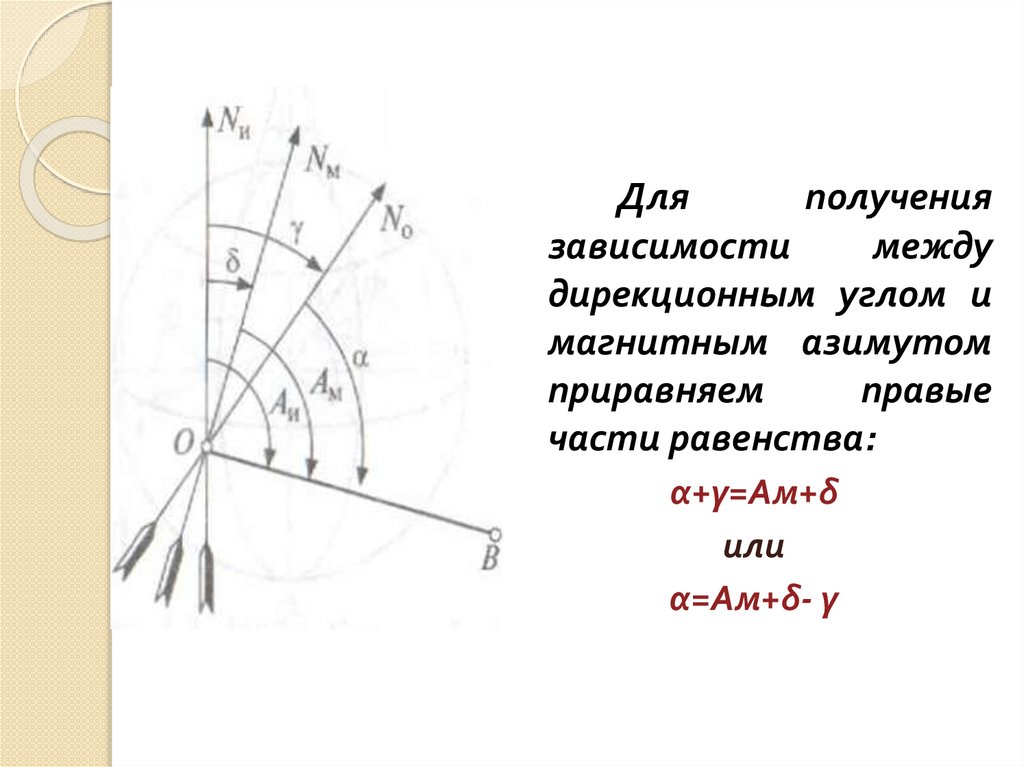
10.

Для
получения
зависимости
между
дирекционным углом и
магнитным азимутом
приравняем
правые
части равенства:
α+γ=Ам+δ
или
α=Ам+δ- γ

11.

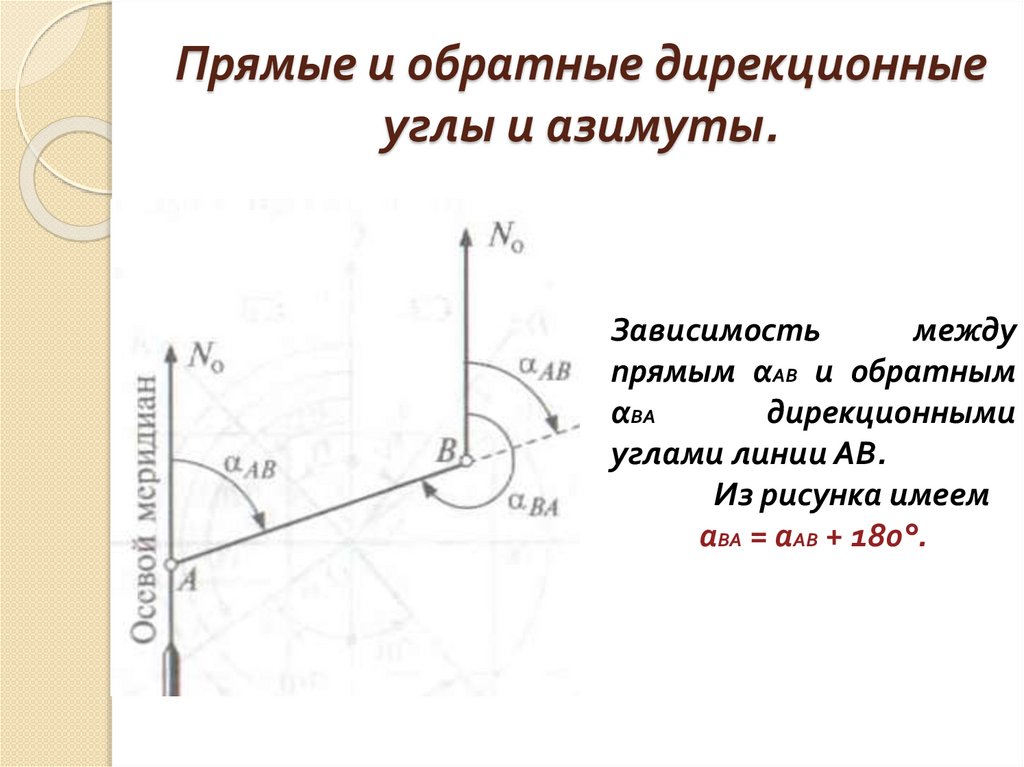
Прямые и обратные дирекционные
углы и азимуты.
Зависимость
между
прямым αАВ и обратным
αВА
дирекционными
углами линии АВ.
Из рисунка имеем
аВА = аАВ + 180°.

12.

Зависимости между истинными азимутами линий
АВ и ВА воспользуемся рисунком. Если γ сближение меридианов между точками А и В, то
АВА = ААВ + 180°- γ.

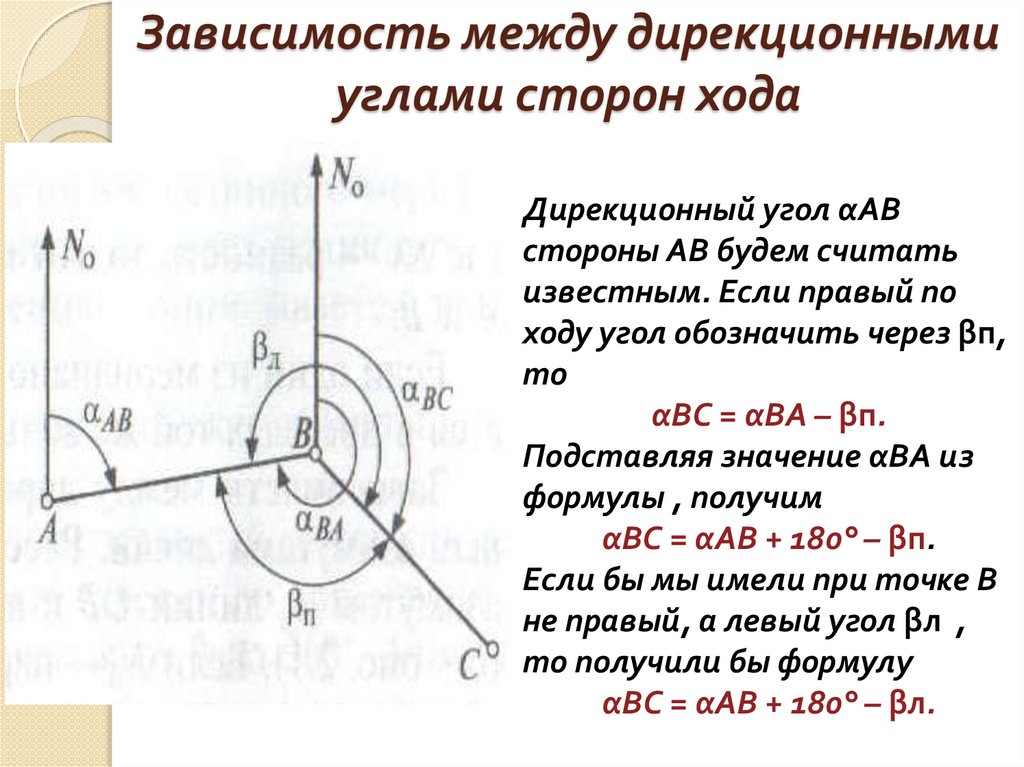
13.

Зависимость между дирекционными
углами сторон хода
Дирекционный угол αАВ
стороны АВ будем считать
известным. Если правый по
ходу угол обозначить через βп,
то
αВС = αВА – βп.
Подставляя значение αВА из
формулы , получим
αВС = αАВ + 180° – βп.
Если бы мы имели при точке В
не правый, а левый угол βл ,
то получили бы формулу
αВС = αАВ + 180° – βл.

14.

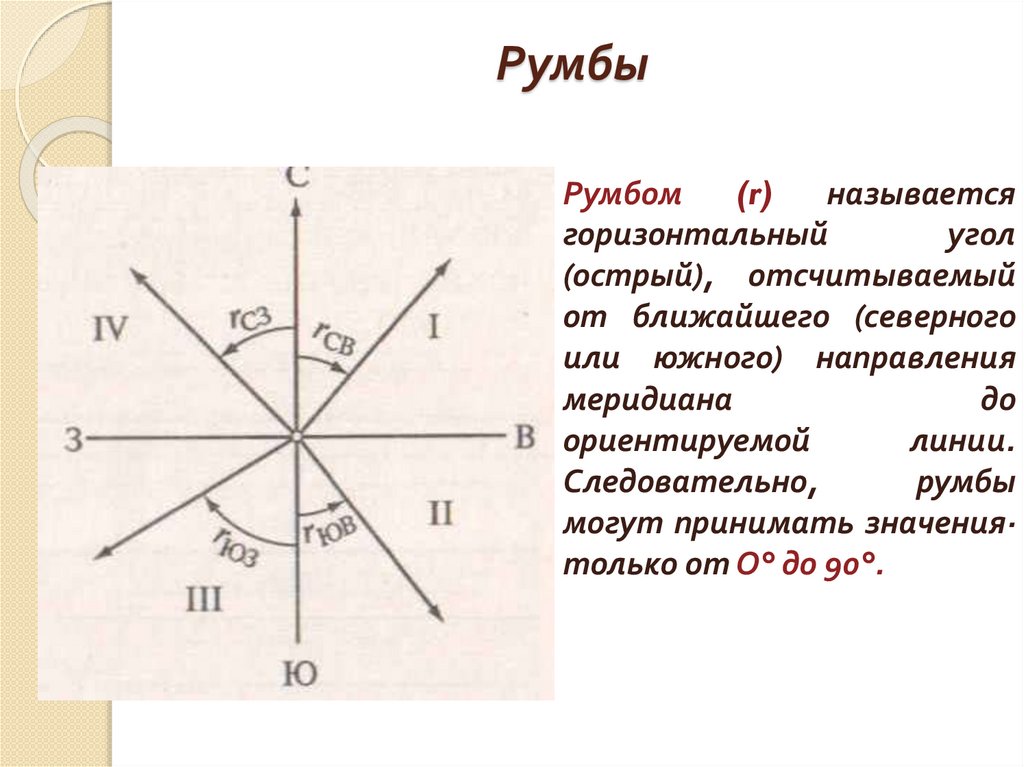
Румбы
Румбом
(r)
называется
горизонтальный
угол
(острый), отсчитываемый
от ближайшего (северного
или южного) направления
меридиана
до
ориентируемой
линии.
Следовательно,
румбы
могут принимать значения·
только от О° до 90°.

15.

Зависимость
между дирекционными
углами
и
румбами
показана на рисунке, а
формулы для перехода
приведены в таблице.

16.

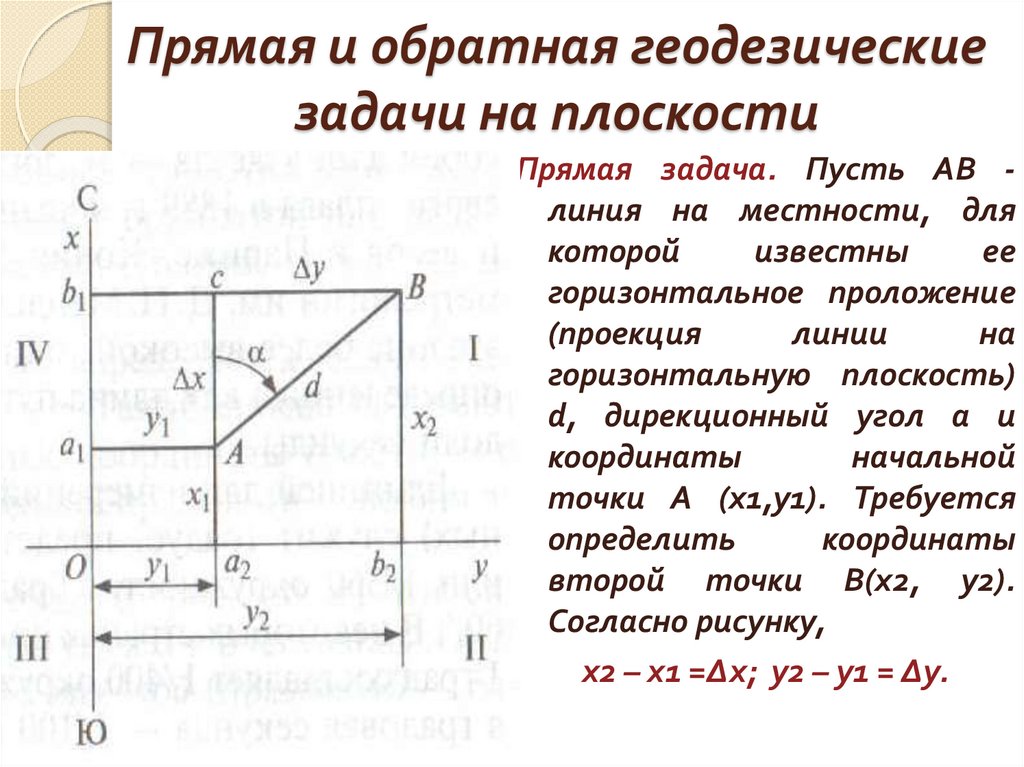
Прямая и обратная геодезические
задачи на плоскости
Прямая задача. Пусть АВ линия на местности, для
которой
известны
ее
горизонтальное проложение
(проекция
линии
на
горизонтальную плоскость)
d, дирекционный угол а и
координаты
начальной
точки А (х1,у1). Требуется
определить
координаты
второй точки В(х2, у2).
Согласно рисунку,
х2 – х1 =Δх; у2 – у1 = Δу.

17.

Разности Δх и Δу координат
точек
последующей
и
предыдущей
называют
приращениями координат.
Из
прямоугольного
треугольника АВС имеем
Δх = dcosα; Δу = dsiпα.
Знаки Δх и Δу зависят от
знаков cosα и sinα (по
таблице).

18.

С помощью румбов Δх и Δу
можно
вычислить
по
следуюшим
формулам:
Δ х = dcos r; Δ у = dsin r.
Тогда искомые координаты
точки В будут следующими:
х2 = х1+ Δх; у1 = у2 + Δу.

19.

Обратная
задача.
По
данным
координатам
точек А и В найти
горизонтальное
проложение d и дирек
ционный угол α.
Из
прямоугольного
треугольника
АВС
имеем
tgα = Δу/Δх;
d = Δ x/cos α = Δ y/sin α.