Similar presentations:
Решение заданий ЕГЭ В6 (часть 2)
1.
МБОУ СОШ №5 – «Школа здоровья и развития» г. РадужныйРешение заданий
В6 (часть 2)
по материалам открытого
банка задач ЕГЭ по
математике
http://mathege.ru/or/ege/Main.html
Учитель математики Семёнова Е.Ю.
2.
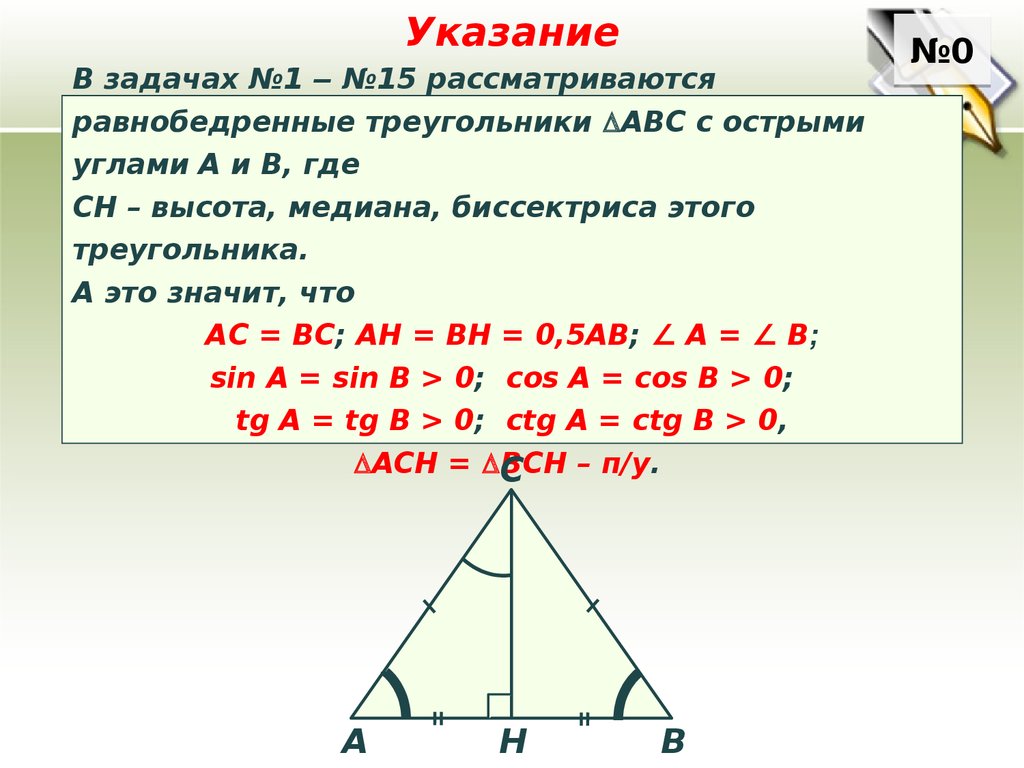
УказаниеВ задачах №1 ‒ №15 рассматриваются
равнобедренные треугольники АВС с острыми
углами А и В, где
СН – высота, медиана, биссектриса этого
треугольника.
А это значит, что
АС = ВС; АН = ВН = 0,5АВ; ∠ A = ∠ В;
sin A = sin B > 0; cos A = cos B > 0;
tg A = tg В > 0; сtg А = ctg B > 0,
ACH = BCH
– п/у.
C
A
Н
B
№0
3.
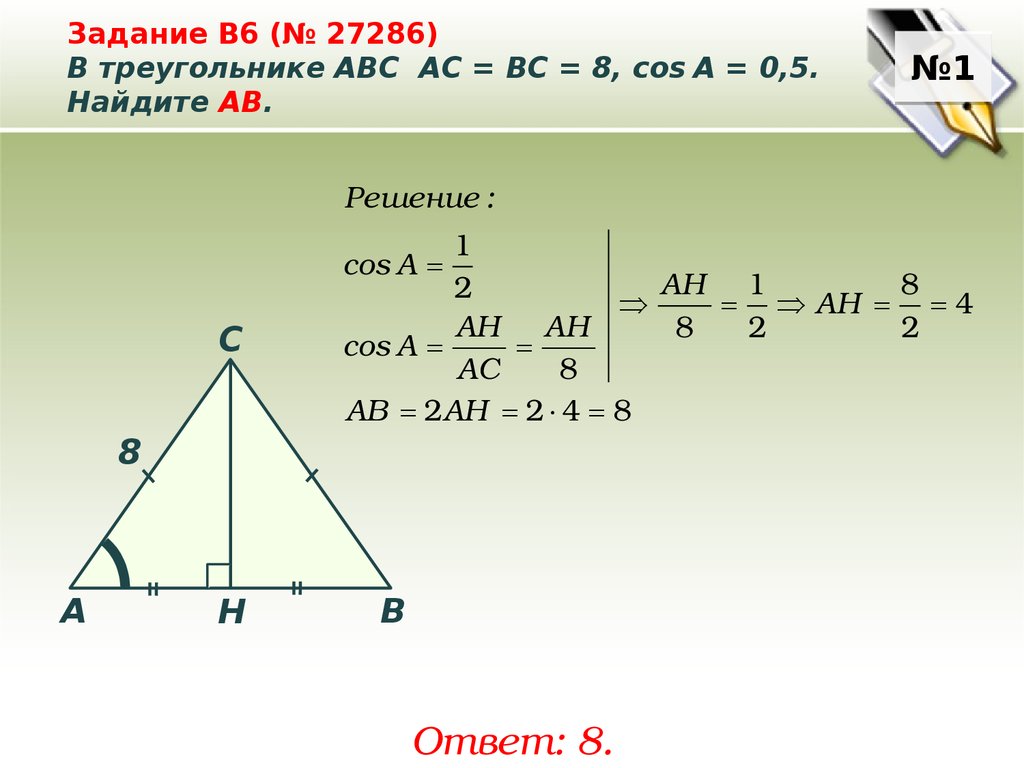
Задание B6 (№ 27286)В треугольнике ABC АC = ВС = 8, cos A = 0,5.
Найдите AВ.
№1
Решение :
C
1
cos А
АН 1
8
2
АН 4
АН АН
8
2
2
cos А
АС
8
АВ 2АН 2 4 8
8
A
Н
B
Ответ: 8.
4.
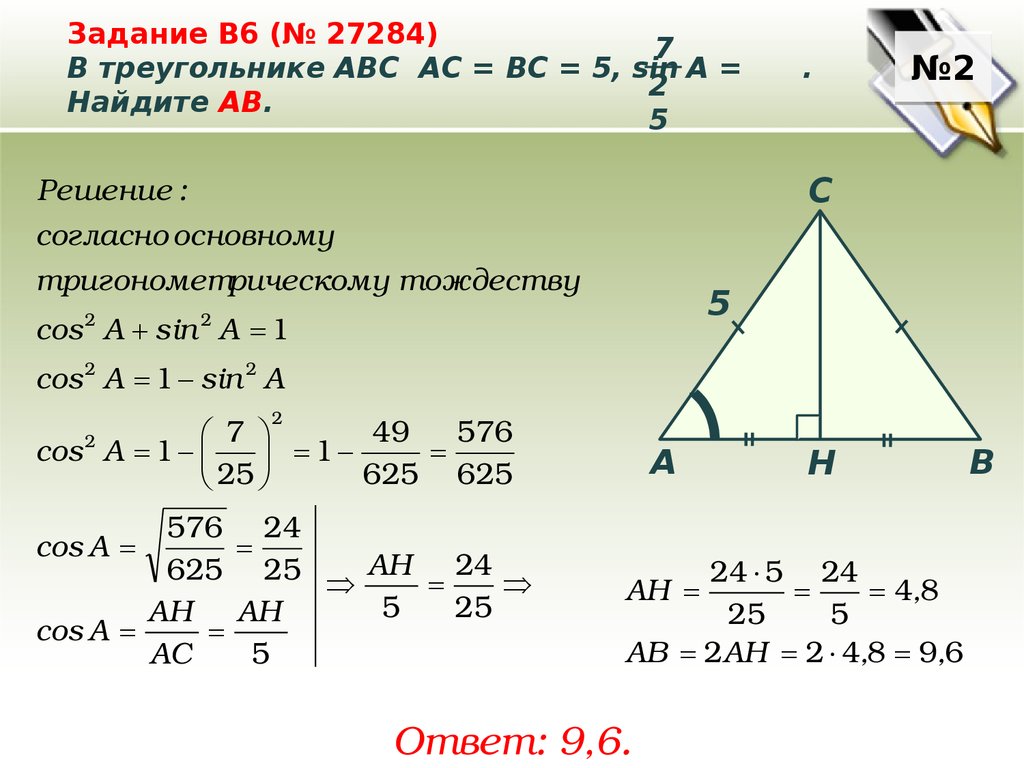
Задание B6 (№ 27284)7
В треугольнике ABC АC = ВС = 5, sin A =
2
Найдите AВ.
5
.
№2
C
Решение :
согласно основному
тригонометрическому тождеству
5
cos А sin А 1
2
2
cos 2 А 1 sin 2 А
2
49
576
7
2
cos А 1
1
625 625
25
576 24
625 25 АН 24
5
25
АН АН
cos А
АС
5
cos А
A
Н
24 5 24
4,8
25
5
АВ 2АН 2 4,8 9,6
АН
Ответ: 9,6.
B
5.
Задание B6 (№ 27288)В треугольнике ABC АC = ВС = 7, tg33
A=
4√33
Найдите AВ.
Решение :
.
№3
согласно тригонометрическому тождеству
1
tg A 1
;
2
cos A
2
33
4 33
33
4
C
2
33
1
1
2
4
cos
A
33
1
1
16
cos 2 A
49
1
A
16 cos 2 A
16
4
2
cos A
cos A
AH 4
49
7
АН 4
AH AH
7
7
cos A
AC
7
АВ 2АН 2 4 8
7
Н
Ответ: 8.
B
6.
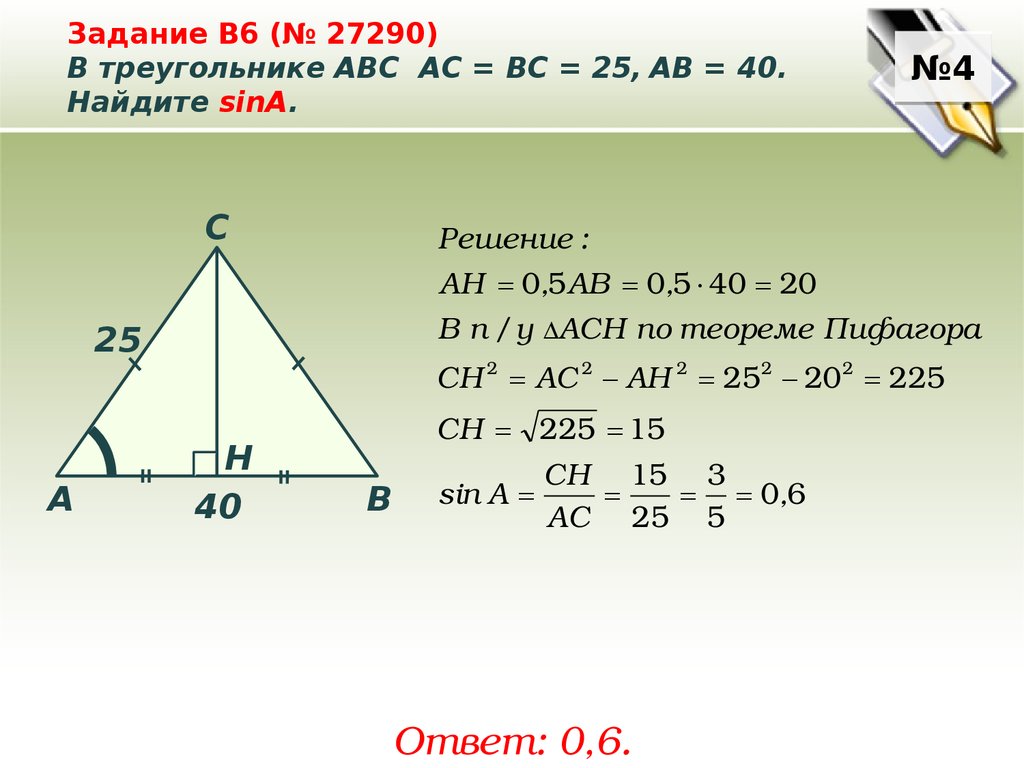
Задание B6 (№ 27290)В треугольнике ABC АC = ВС = 25, AB = 40.
Найдите sinA.
C
Решение :
АН 0,5 АВ 0,5 40 20
В п / у ΔАСН по теореме Пифагора
25
A
№4
СН 2 АС 2 АН 2 25 2 202 225
Н
40
B
СН 225 15
CH 15 3
sin А
0,6
AC 25 5
Ответ: 0,6.
7.
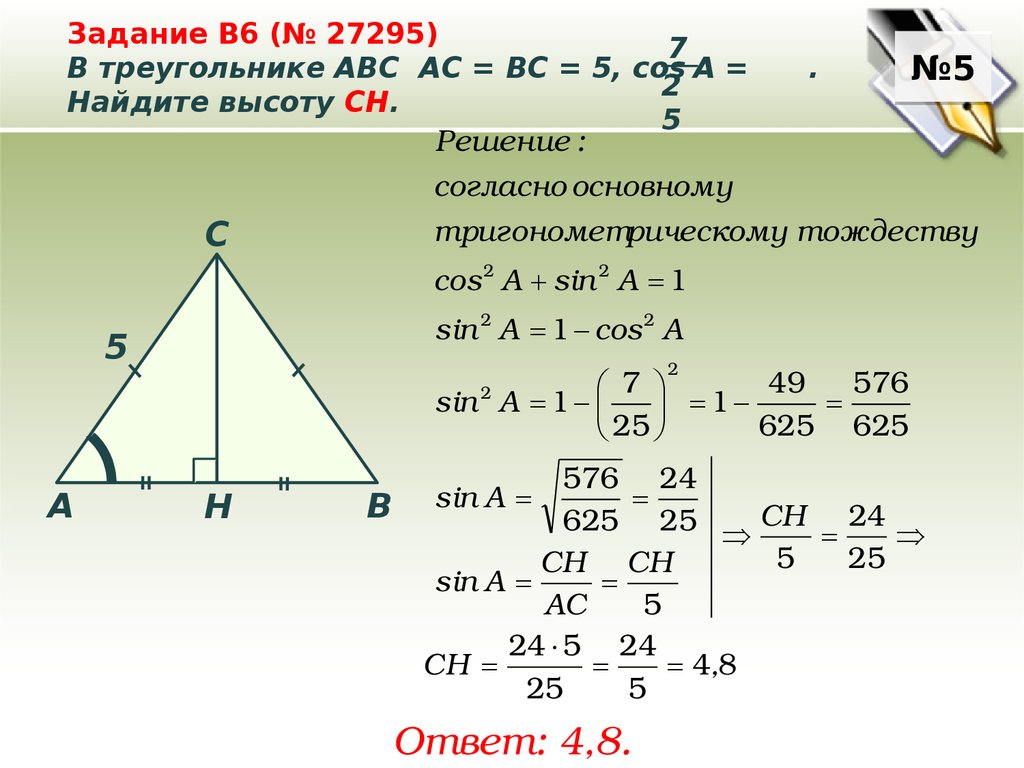
Задание B6 (№ 27295)7
В треугольнике ABC АC = ВС = 5, cos A =
2
Найдите высоту CH.
5
.
№5
Решение :
согласно основному
тригонометрическому тождеству
C
cos 2 А sin 2 А 1
sin 2 А 1 cos 2 А
5
A
2
49
576
7
sin 2 А 1
1
625 625
25
Н
B
576 24
sin А
625 25 CН 24
5
25
CН CН
sin А
АС
5
24 5 24
СН
4,8
25
5
Ответ: 4,8.
8.
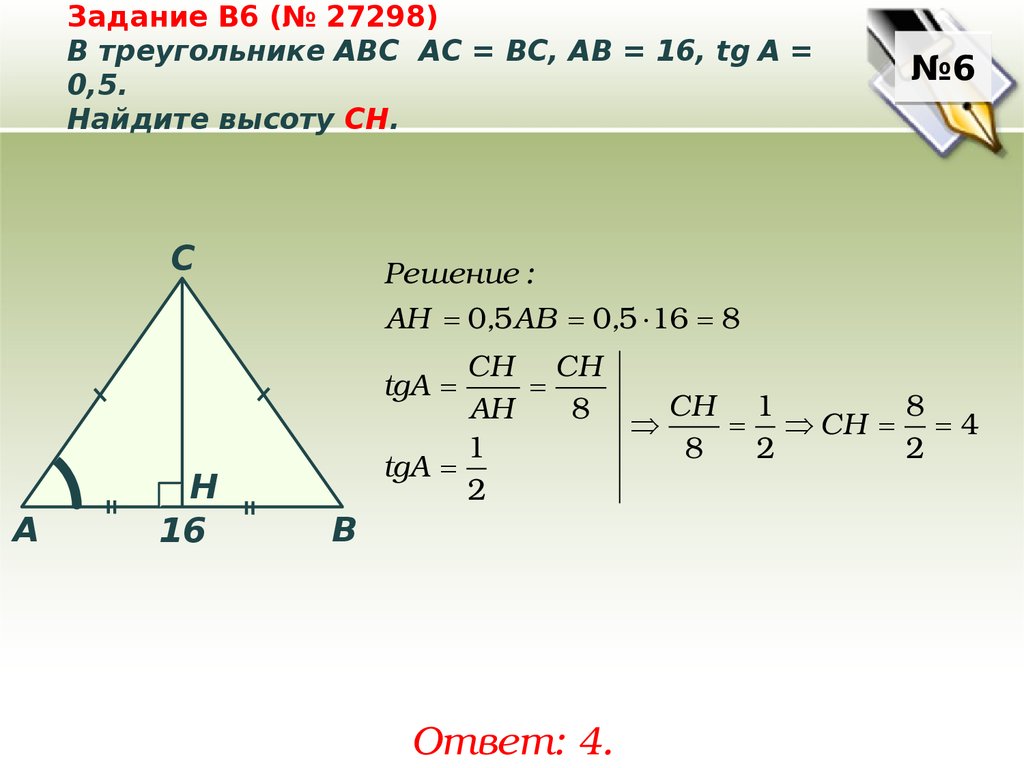
Задание B6 (№ 27298)В треугольнике ABC АC = ВС, AB = 16, tg A =
0,5.
Найдите высоту CH.
C
№6
Решение :
АН 0,5 АВ 0,5 16 8
CH CH
CH 1
8
AH
8
CH 4
1
8
2
2
tgA
2
tgA
A
Н
16
B
Ответ: 4.
9.
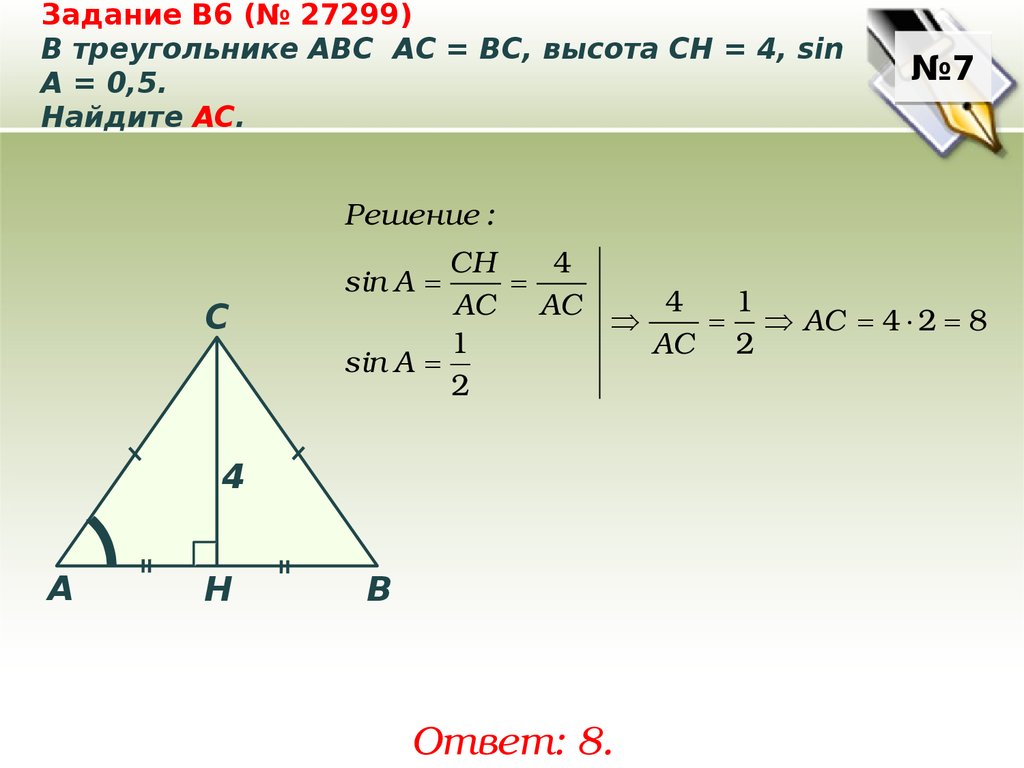
Задание B6 (№ 27299)В треугольнике ABC АC = ВС, высота СН = 4, sin
A = 0,5.
Найдите AC.
№7
Решение :
C
CH
4
sin A
4
1
AC AC
AC 4 2 8
1
AC 2
sin A
2
4
A
Н
B
Ответ: 8.
10.
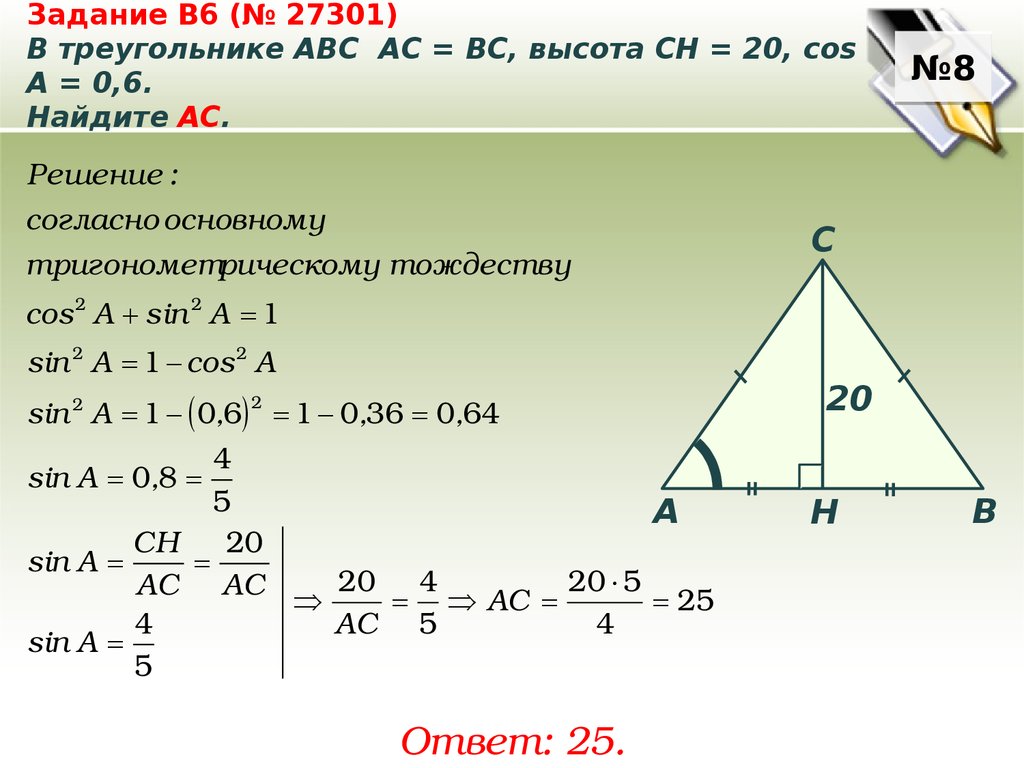
Задание B6 (№ 27301)В треугольнике ABC АC = ВС, высота СН = 20, cos
A = 0,6.
Найдите AC.
№8
Решение :
согласно основному
тригонометрическому тождеству
C
cos 2 А sin 2 А 1
sin 2 А 1 cos 2 А
sin 2 А 1 0,6 1 0,36 0,64
2
4
5
A
CH
20
sin A
20 4
20 5
AC AC
AC
25
4
AC 5
4
sin A
5
sin А 0,8
Ответ: 25.
20
Н
B
11.
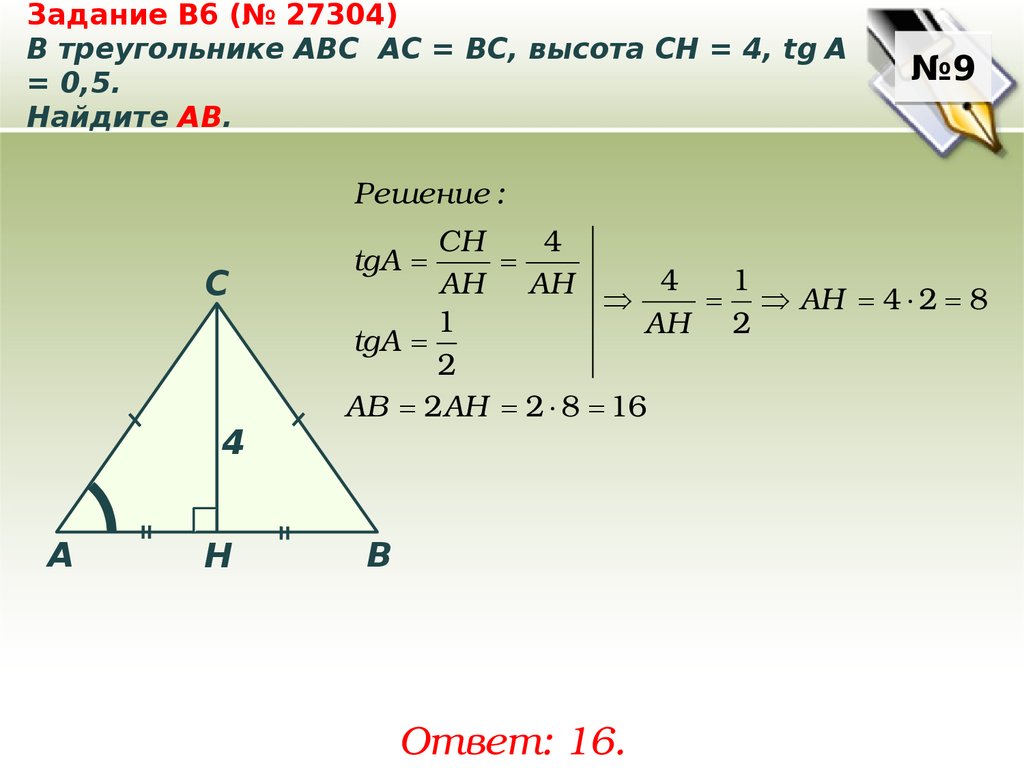
Задание B6 (№ 27304)В треугольнике ABC АC = ВС, высота СН = 4, tg A
= 0,5.
Найдите AB.
№9
Решение :
C
4
A
Н
CH
4
4
1
AH AH
AH 4 2 8
1
AH 2
tgА
2
AB 2AH 2 8 16
tgА
B
Ответ: 16.
12.
Задание B6 (№ 27305)В треугольнике ABC АC = ВС, высота СН = 7, AB =
48.
Найдите sinA.
№1
0
Решение :
АН 0,5 АВ 0,5 48 24
В п / у ΔАСН по теореме Пифагора
C
AC 2 АH 2 CН 2 242 72 625
7
A
Н
48
B
AC 625 25
CH
7
28
sin А
0,28
AC 25 100
Ответ: 0,28.
13.
Задание B6 (№ 27307)В треугольнике ABC АC = ВС, высота СН = 4, AB =
16.
Найдите tgA.
C
Решение :
АН 0,5 АВ 0,5 16 8
CH 4 1
tgА
0,5
AH 8 2
4
A
Н
16
B
Ответ: 0,5.
№1
1
14. Используемые материалы
• http://mathege.ru/or/ege/Main − Материалы открытогобанка заданий по математике 2013 года




 mathematics
mathematics








