Решение заданий ЕГЭ уровня С4 2013 года (2 часть)

1.

МБОУ СОШ БАГАЕВСКАЯ СРЕДНЯЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 1
Решение заданий ЕГЭ уровня С4
2013 года
(2 часть)
Автор: АЛИМОВА НАДЕЖДА ИВАНОВНА

2.

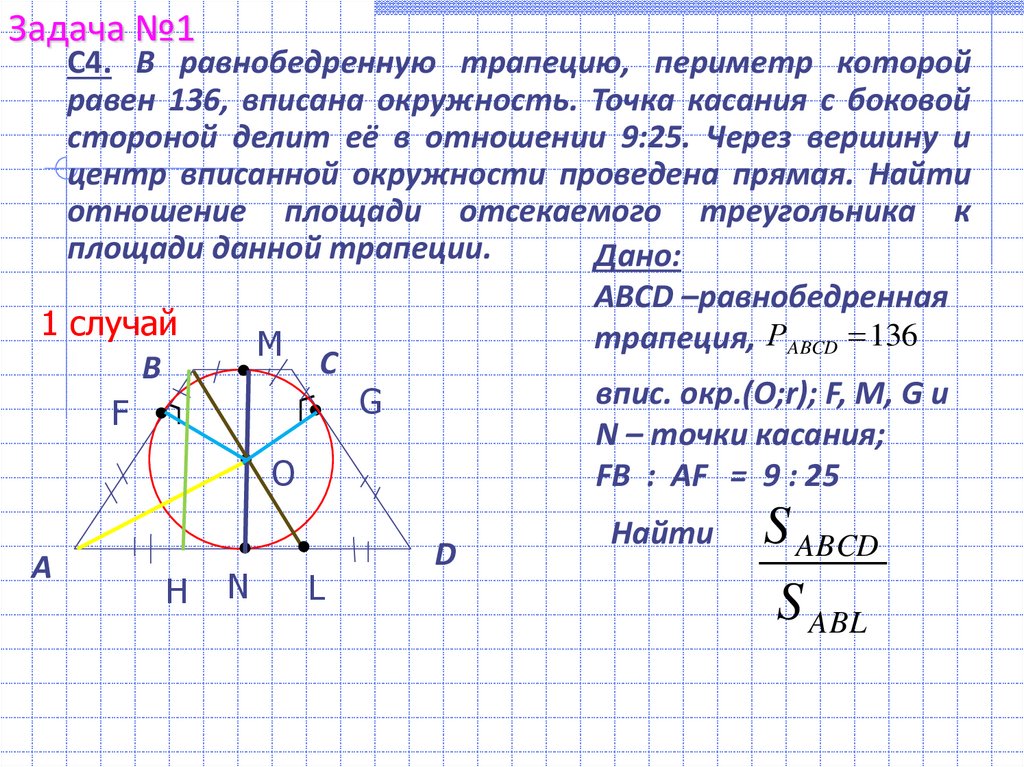
Задача №1
С4. В равнобедренную трапецию, периметр которой
равен 136, вписана окружность. Точка касания с боковой
стороной делит её в отношении 9:25. Через вершину и
центр вписанной окружности проведена прямая. Найти
отношение площади отсекаемого треугольника к
площади данной трапеции.
Дано:
ABCD –равнобедренная
1 случай
трапеция, РABCD 136
M
C
B
впис. окр.(О;r); F, M, G и
G
F
N – точки касания;
О
FB : AF = 9 : 25
A
H
N
L
D
Найти
S ABCD
S ABL

3.

M
B
C
F
О
A
H
N
L
G
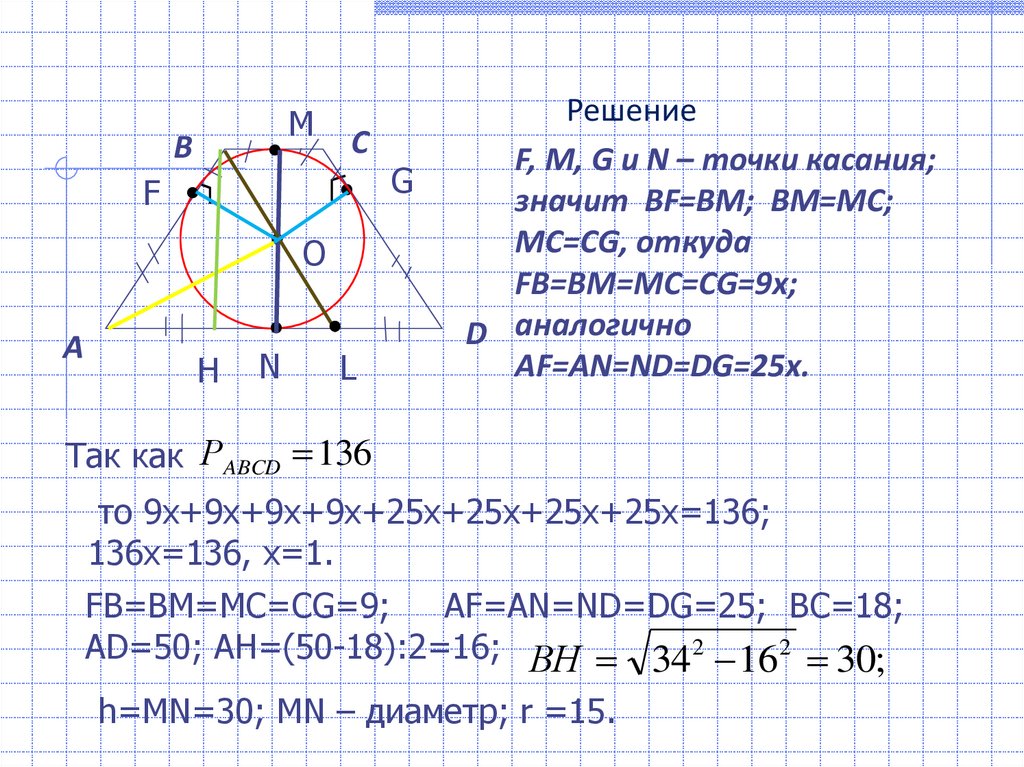
Решение
F, M, G и N – точки касания;
значит BF=BM; BM=MC;
MC=CG, откуда
FB=BM=MC=CG=9x;
D аналогично
AF=AN=ND=DG=25x.
Так как РABCD 136
то 9х+9х+9х+9х+25х+25х+25х+25х=136;
136х=136, х=1.
FB=BM=MC=CG=9;
AF=AN=ND=DG=25; BC=18;
AD=50; AH=(50-18):2=16; ВH 34 2 16 2 30;
h=MN=30; MN – диаметр; r =15.

4.

M
B
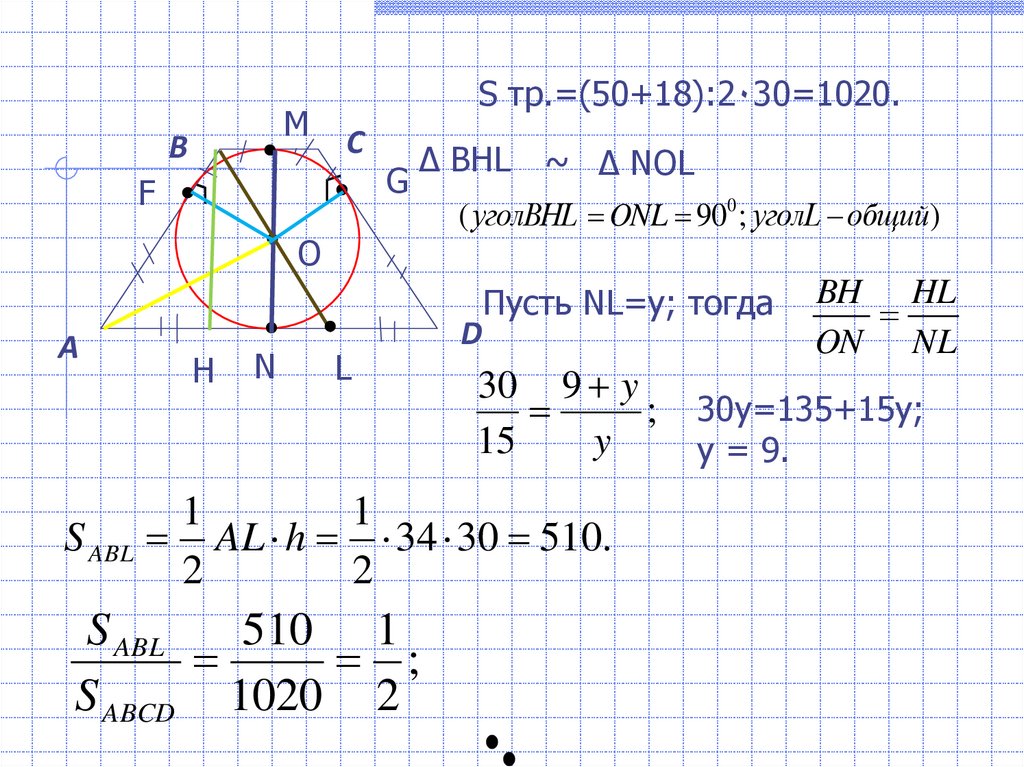
S тр.=(50+18):2٠30=1020.
C
F
G
∆ BHL ~ ∆ NOL
О
A
S ABL
H
N
L
( уголBHL ONL 900 ; уголL общий)
D
Пусть NL=y; тогда
30 9 y
;
15
y
1
1
AL h 34 30 510.
2
2
S ABL
510 1
;
S ABCD 1020 2
BH HL
ON NL
30y=135+15y;
y = 9.

5.

2 случай
AO 252 152 625 225 850 ;
B
M
F
C
I
G
О
A
N
∆AON=∆AFO (AN=AF, FO=ON,
AO- общая). Пусть /FAO=α; /
NDO= α; / NDG=2α; в ∆ APD:
D угол APD= 180 0 3
15
225
9
3
850
34
850
34
sin ADC sin 2 2 sin cos ;
Из ∆ AON:
sin
9
25
5
;
34
34
34
5
3
15
sin 2 2
;
34 34 17
cos 1 sin 2 1

6.

B
M
F
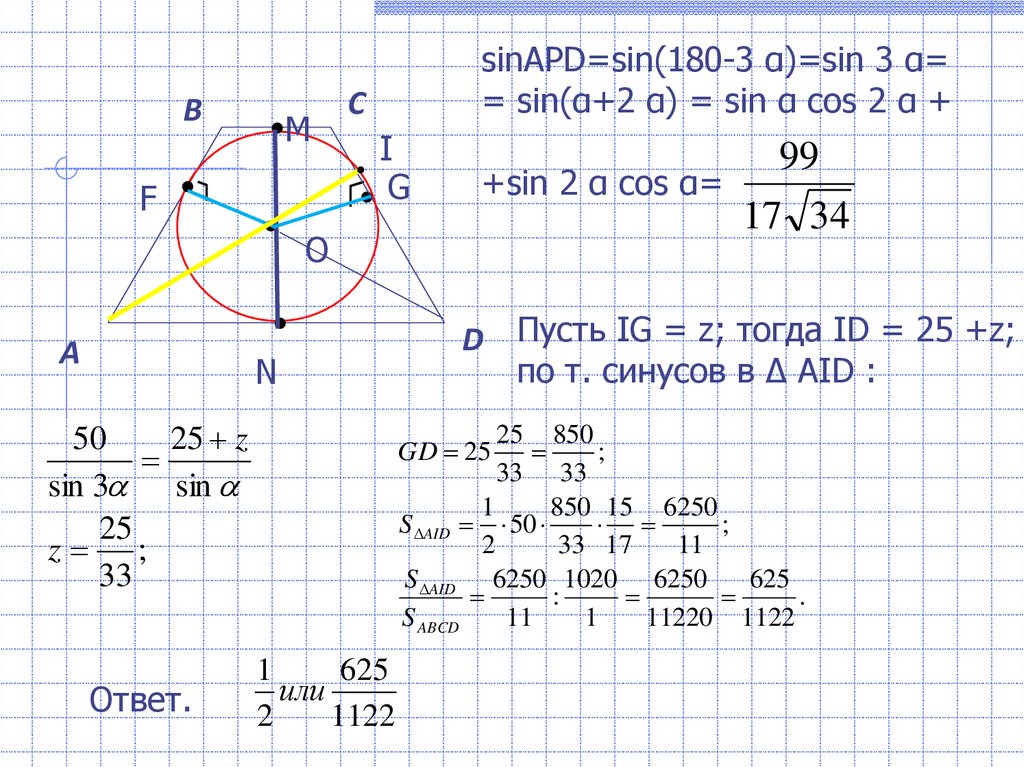
sinAPD=sin(180-3 α)=sin 3 α=
= sin(α+2 α) = sin α cos 2 α +
C
I
G
О
A
N
50
25 z
sin 3 sin
25
z ;
33
Ответ.
99
+sin 2 α cos α=
17 34
D Пусть IG = z; тогда ID = 25 +z;
по т. синусов в ∆ AID :
25 850
;
33 33
1
850 15 6250
S AID 50
;
2
33 17
11
S AID 6250 1020 6250
625
:
.
S ABCD
11
1
11220 1122
GD 25
1
625
или
2
1122

7.

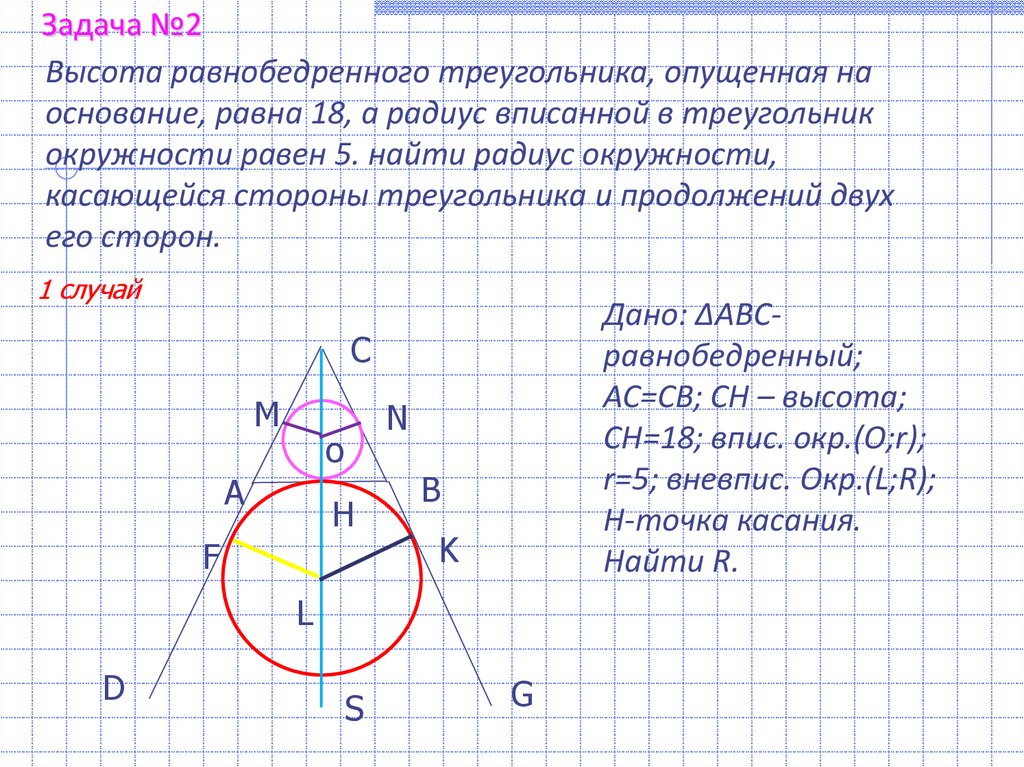
Задача №2
Высота равнобедренного треугольника, опущенная на
основание, равна 18, а радиус вписанной в треугольник
окружности равен 5. найти радиус окружности,
касающейся стороны треугольника и продолжений двух
его сторон.
1 случай
Дано: ∆АВСравнобедренный;
АС=СВ; СН – высота;
СН=18; впис. окр.(О;r);
r=5; вневпис. Окр.(L;R);
Н-точка касания.
Найти R.
С
М
N
о
А
Н
F
В
K
L
D
S
G

8.

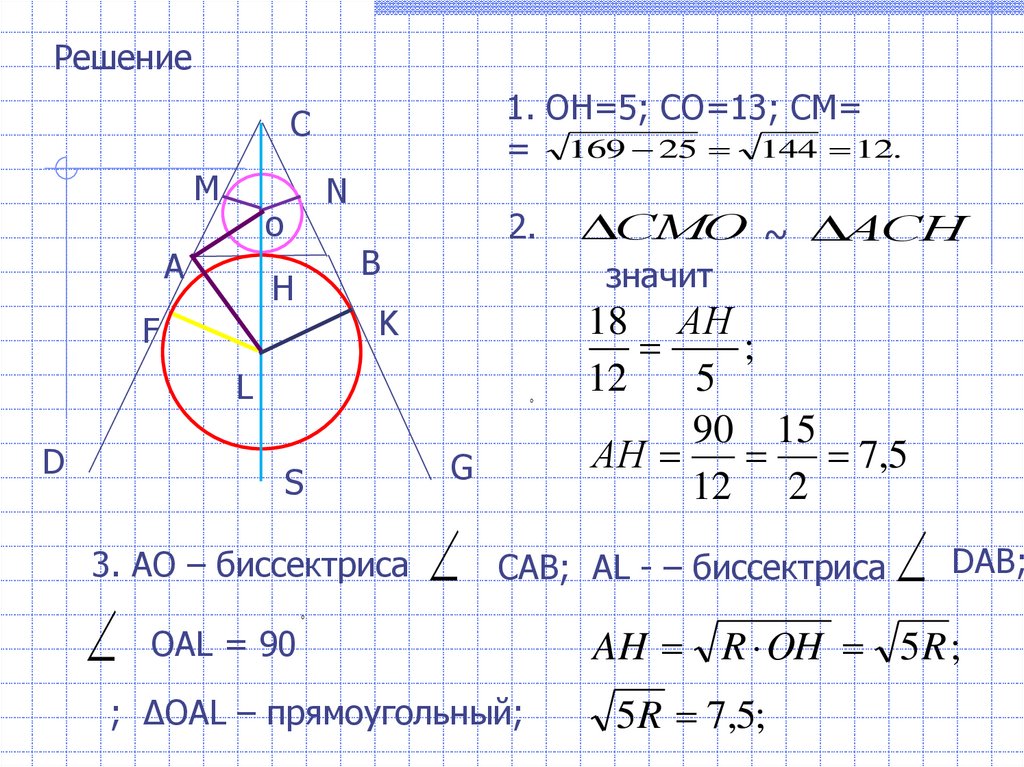
Решение
1. ОН=5; СО=13; СМ=
= 169 25 144 12.
С
М
N
о
А
2.
В
Н
значит
K
F
L
D
S
3. АО – биссектриса
ОАL = 90
СМО ~ АСН
G
18 АН
;
12
5
90 15
АН
7,5
12 2
САВ; АL - – биссектриса
; ∆OAL – прямоугольный;
DAB;
AH R OH 5 R ;
5 R 7,5;

9.

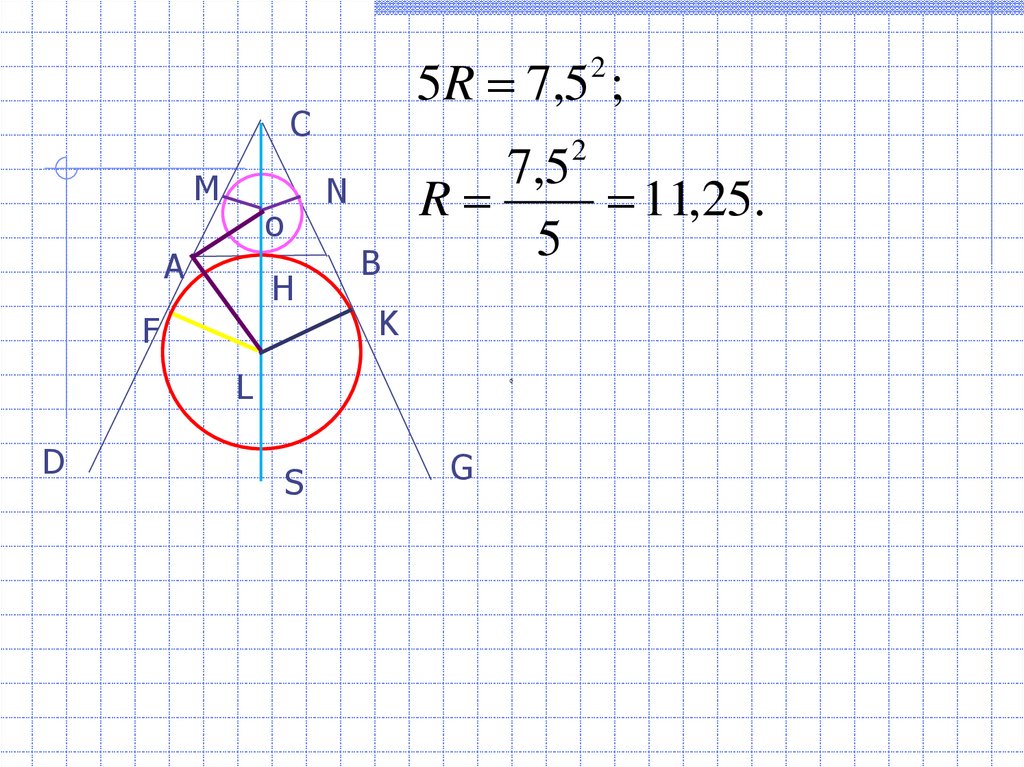
5R 7,5 ;
2
С
М
N
о
А
2
Н
F
В
7,5
R
11,25.
5
K
L
D
S
G

10.

M
A
F
C
O
B
H
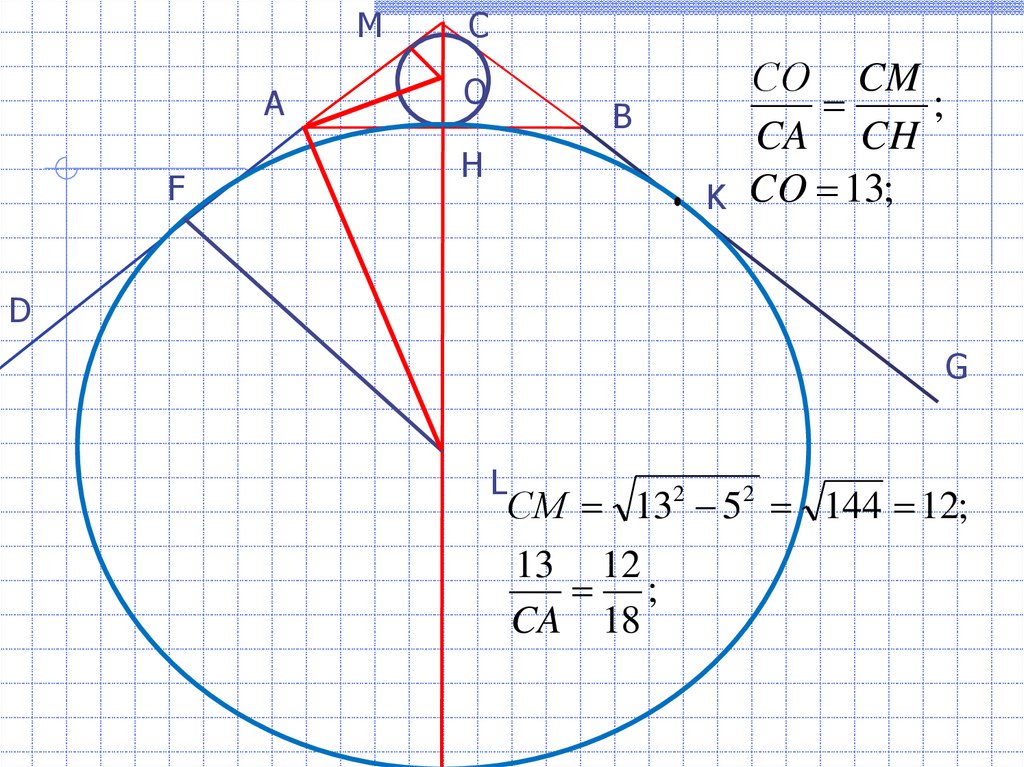
СO CM
;
CA CH
K CO 13;
D
G
L
СM 132 52 144 12;
13 12
;
CA 18

11.

CA=19,5;
AH=7,5;
OAL прямоуголь ный(доказано )
AL (5 R ) R;
AL R 2 7,52 ;
(5 R ) R R 2 7,52 ;
R = 11,25.
Ответ. R=11,25

12.

Работа выполнена на основе заданий
открытого банка ЕГЭ – 2013
29.03.2013 года