Принцип Даламбера для материальной точки. Лекция 2

1.

Принцип Даламбера для
материальной точки

2.

F ma
и
и
F, равная по модулю произведению массы
Сила
точки на ее ускорение и направленная в сторону,
противоположную ускорению, называется силой
инерции (даламберовой силой).

3.

Принцип Даламбера для точки
Если в каждый данный момент к действующим на
точку активным силам и силам реакции связей
прибавить силу инерции, то полученная система сил
будет находиться в равновесии и по отношению к
ней будут справедливы все уравнения статики.
F R F 0
а
и
Значение принципа Даламбера состоит в том, что он позволяет
при решении динамических задач составлять уравнения
движения в форме уравнений равновесия.

4.

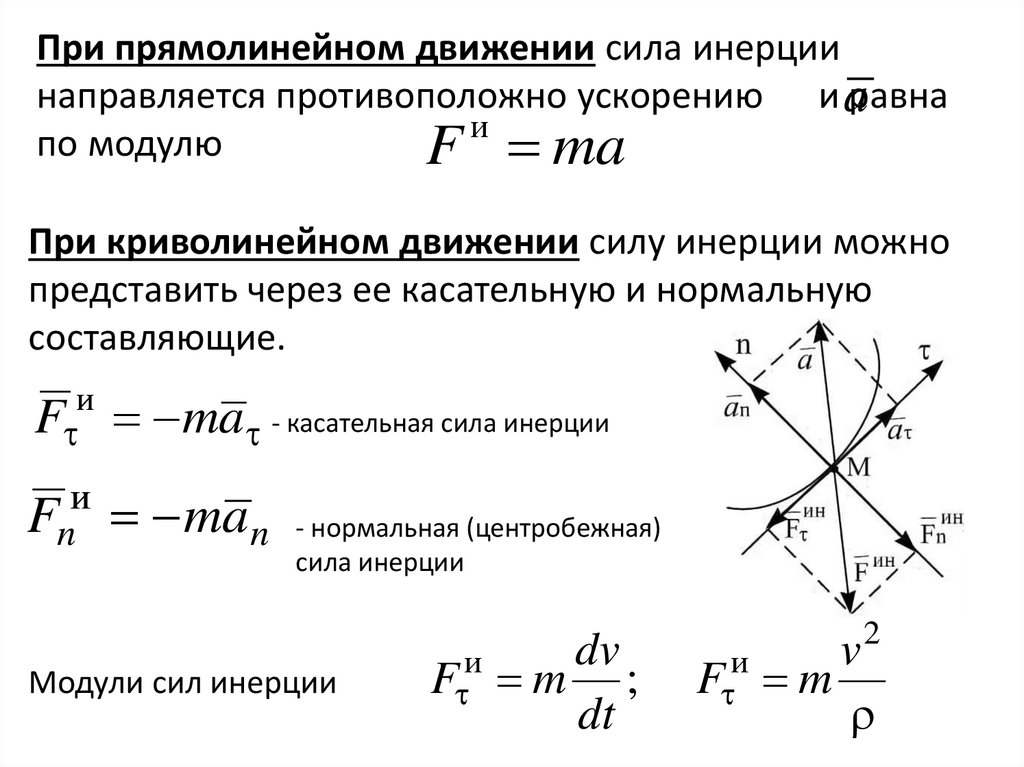
При прямолинейном движении сила инерции
направляется противоположно ускорению и aравна
и
по модулю
F ma
При криволинейном движении силу инерции можно
представить через ее касательную и нормальную
составляющие.
и
F
ma - касательная сила инерции
и
Fn
ma n
- нормальная (центробежная)
сила инерции
Модули сил инерции
F и
dv
m ;
dt
F и
2
v
m

5.

Принцип Даламбера для
механической системы

6.

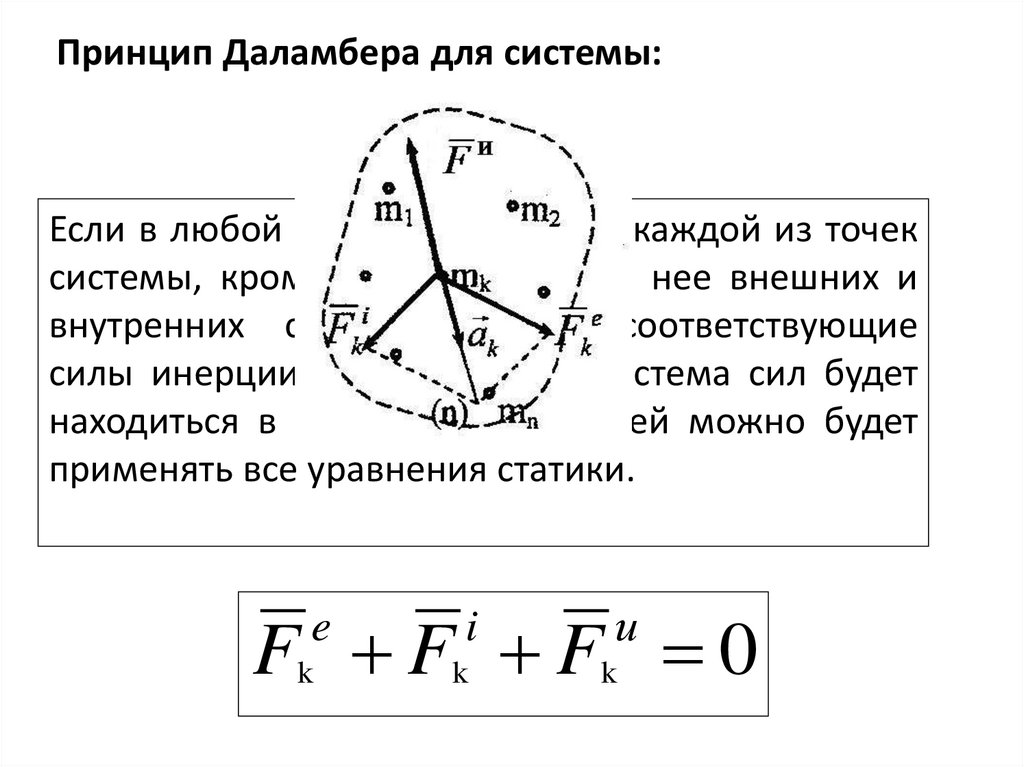
Принцип Даламбера для системы:
Если в любой момент времени к каждой из точек
системы, кроме действующих на нее внешних и
внутренних сил, приложить соответствующие
силы инерции, то полученная система сил будет
находиться в равновесии и к ней можно будет
применять все уравнения статики.
Fk Fk Fk 0
e
i
и

7.

R 0;
M 0,
геометрическая сумма сил, находящихся в
равновесии, и сумма их моментов
относительно любого центра О равны нулю
Тогда на основании принципа Даламбера:
e
i
и
F
F
F
k
k
k 0;
e
i
и
M O Fk M O Fk M O Fk 0.
Введем обозначения:
R F
и
Главный вектор сил
инерции
F
e
k
M Oи M O Fkи
и
k
R 0;
и
Главный момент сил инерции относительно центра
О.
M F M
O
e
k
и
O
0

8.

Главный вектор и главный
момент сил инерции твердого
тела.

9.

Главный
вектор
сил
инерции
тела,
совершающего
любое
движение,
равен
произведению массы тела на ускорение его
центра масс и направлен противоположно этому
ускорению.
R maC
и
где
m
– масса
тела;
aC – ускорение центра масс тела.

10.

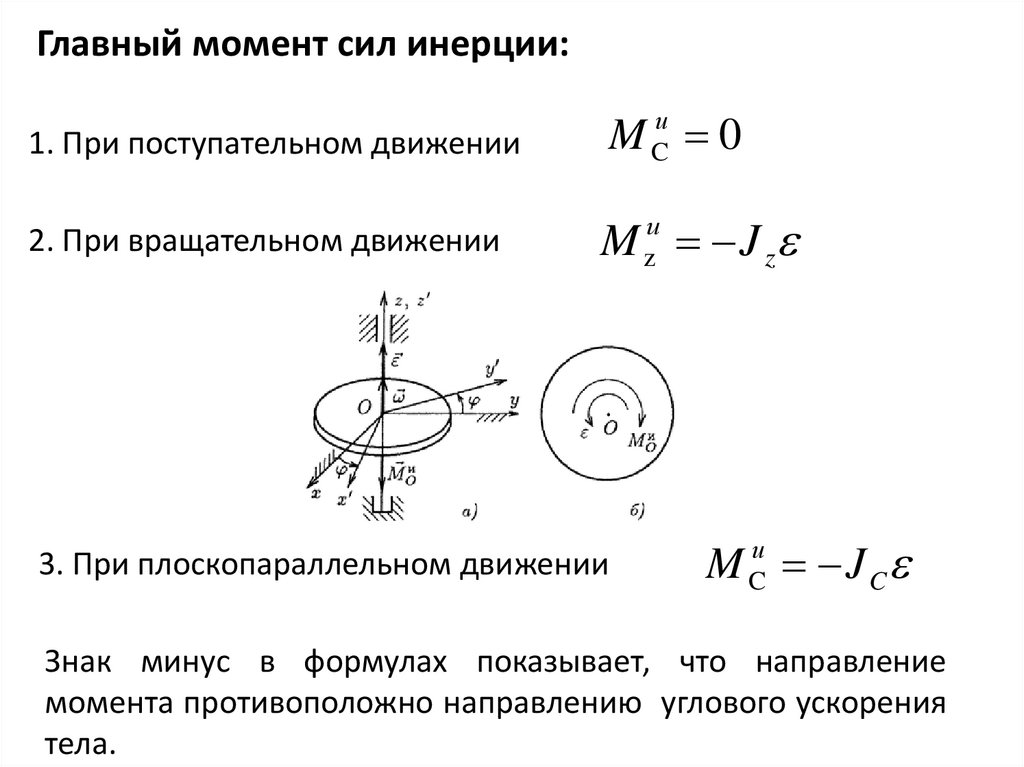
Главный момент сил инерции:
1. При поступательном движении
M 0
2. При вращательном движении
M zи J z
и
C
3. При плоскопараллельном движении
M Cи J C
Знак минус в формулах показывает, что направление
момента противоположно направлению углового ускорения
тела.

11.

Принцип Даламбера
составления
уравнений
несвободной системы.
дает единый метод
движения
любой
С его помощью решаются задачи, в которых,
зная движение системы, нужно определить реакции
наложенных связей.
Метод решения, основанный на принципе
Даламбера, называется методом кинетостатики.
Кроме того, принципом можно пользоваться для
составления дифференциальных уравнений движения,
в частности, для определения ускорений движущихся
тел.