Similar presentations:
Основные законы динамики материальной точки (лекция № 2)
1.
Лекция № 2«ОСНОВНЫЕ ЗАКОНЫ
ДИНАМИКИ МАТЕРИАЛЬНОЙ
ТОЧКИ»
2.
УЧЕБНЫЕ ВОПРОСЫ :1. Первый закон Ньютона. Инерциальные системы
отсчета.
2. Второй и третий законы Ньютона.
3. Единицы измерения механических величин.
4. Принцип относительности Галилея. Закон сложения
скоростей.
5. Силы в природе.
6. Законы изменения и сохранения импульса. Центр
масс.
7. Основные положения статики.
8. Динамика материальной точки, движущейся по
окружности.
9. Динамика вращательного движения твердого тела с
неподвижной осью вращения
3.
Вопрос 1.ПЕРВЫЙ ЗАКОН НЬЮТОНА.
ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ
ОТСЧЕТА
4.
СИЛА– это векторная физическая
величина, характеризующая
взаимодействие между
телами.
Обозначение F,
измеряется в [H]
5.
ПЕРВЫЙ ЗАКОН НЬЮТОНА(закон инерции)
Существуют в природе такие
системы отсчета, относительно
которых любое тело сохраняет
состояние покоя или равномерного
прямолинейного движения, если на
него не действуют другие тела
или действие этих тел
скомпенсировано.
6.
Такие системы отсчетаназывают
ИНЕРЦИАЛЬНЫМИ (ИСО)
Любые две ИСО движутся
относительно друг друга
равномерно и прямолинейно
7.
Вопрос 2.ВТОРОЙ И ТРЕТИЙ
ЗАКОНЫ НЬЮТОНА
8.
ВТОРОЙ ЗАКОН НЬЮТОНАВ инерциальной системе отсчёта
ускорение материальной точки
прямо пропорционально
действующей силе (или
равнодействующей всех
и
сил)
направлено вдоль неё a ~ F .
Коэффициент
пропорциональности в СИ
обозначается через m и
называется массой
9.
В системе СИ второй закон Ньютонаможет быть представлен в
следующем общем виде
ma F ; (max Fx ; ma F ).
ИМПУЛЬС
(или количество движения)
p mv
10.
Посколькуdv dp
ma m
,
dt dt
то второй закон Ньютона может
быть представлен в так
называемой импульсной форме:
dp
F
dt
11.
МАССАкачественно характеризует
инертность тела, т.е. его
способность изменять
состояние движения или покоя
под действием силы:
F
const m.
a
12.
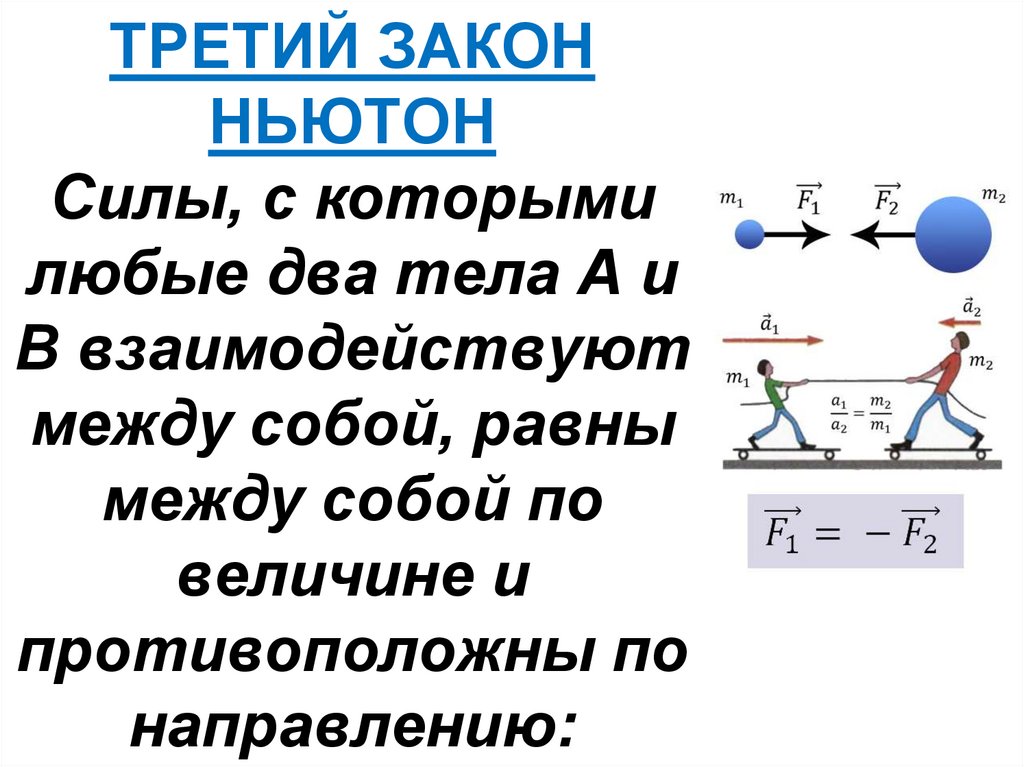
ТРЕТИЙ ЗАКОННЬЮТОН
Силы, с которыми
любые два тела А и
В взаимодействуют
между собой, равны
между собой по
величине и
противоположны по
направлению:
13.
Вопрос 3.ЕДИНИЦЫ ИЗМЕРЕНИЯ
МЕХАНИЧЕСКИХ ВЕЛИЧИН
14.
В физике принято какие-либовеличины принимать за
основные (сравниваемые с
эталоном), а единицы
измерения других
(производных) величин
вводить пользуясь формулами
зависимости производной
величины от основных.
15.
16.
1 метр (м) – это расстояние, проходимое ввакууме ЭМВ за 1/299 792 458 долю секунды (земной
меридиан около 40000 км);
1 секунда (с) – это промежуток времени равный
9 192 631 770 периодам излучения, соответствующего
переходу между двумя сверхтонкими уровнями
основного состояния атома цезия-133 (в сутках
содержится примерно 86400 с );
1 килограмм (кг) – это масса платиново-иридиевой
эталонной гири, хранящейся в Международной
палате мер и весов, находящейся в Севре (бывшее
предместье Парижа, ныне с ним слившееся).
17.
1 ньютон (Н) - единица силы – это сила,которая телу массой 1 кг сообщает
ускорение 1 м/с2
кг м
F 2
с
кг м
- единица импульса – это импульс
1
2
тела массой 1 кг, движущегося со
с
скоростью 1 м/с, [p] = кг м/с
18.
КИЛОГРАММ-СИЛА1 кгс – это сила, которая телу
массой 1 кг сообщает
нормальное ускорение
свободного падения g=9,80655
м/с2 (которое имеет место на
широте Севра).
1 кгс = g(Н) = 9,80655 Н = 9,81 Н
19.
Вопрос 4.ПРИНЦИП
ОТНОСИТЕЛЬНОСТИ
ГАЛИЛЕЯ. ЗАКОН
СЛОЖЕНИЯ СКОРОСТЕЙ
20.
ПРИНЦИПОТНОСИТЕЛЬНОСТИ
ГАЛИЛЕЯ
Законы механики инвариантны
(не меняют свой вид)
относительно перехода из
одной ИНЕРЦИАЛЬНОЙ
СИСТЕМЫ ОТСЧЕТА в другую
21.
22.
Вопрос 5.СИЛЫ В ПРИРОДЕ
23.
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯлюбые два тела притягиваются между
собой, причём величина силы притяжения
двух точечных тел прямо
пропорциональна величинам их масс и
обратно пропорциональна квадрату
расстояния между ними:
F
m1 m2
r
2
,
ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ
6.685 10
11 3
м / кг с
2
24.
ЭЛЕКТРОМАГНИТНЫЕВЗАИМОДЕЙСТВИЯ,
определяемые законом
Кулона и силой Лоренца,
значительно превосходят
гравитационные
25.
СИЛА ТРЕНИЯ– это касательная составляющая
силы, возникающей при
соприкосновении двух
поверхностей
Fn N
Fск N
СИЛА ТРЕНИЯ ПОКОЯ
СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
СИЛА ТРЕНИЯ КАЧЕНИЯ
N - нормальная составляющая контактной силы,
называемая силой нормального давления
26.
Воздействующая на данноетело сила со стороны другого
тела, ограничивающего
движение данного тела,
называется
СИЛОЙ РЕАКЦИИ
27.
СИЛА СОПРОТИВЛЕНИЯ– это сила, действующая на
тело, которое движется в
газообразной или жидкой
среде
При достаточно малых
скоростях сила
сопротивления
пропорциональна
скорости
Fc rV
При больших
скоростях
2
F~V
(r - коэффициент
сопротивления)
28.
СИЛА УПРУГОСТИ– это сила, возникающая при
упругой деформации и в
общем случае, как следует из
закона Гука, пропорциональна
деформации
упр
x:F
kx
где k - коэффициент упругости
29.
Вопрос 6.ЗАКОНЫ ИЗМЕНЕНИЯ И
СОХРАНЕНИЯ ИМПУЛЬСА.
ЦЕНТР МАСС
30.
ЗАКОН ИЗМЕНЕНИЯ ИМПУЛЬСАматериальной точки
Изменение импульса материальной
точки равно импульсу действующей
силы
t
p Fdt
0
31.
ПОЛНЫМ ИМПУЛЬСОМ(количеством движения)
системы, состоящей из МТ
называется векторная величина,
равная геометрической сумме
импульсов всех точек системы:
P p1 p2 pn
32.
tt
n
pi ( Fki )dt Fi dt
0 k 1
0
k i
33.
Произведя суммированиеаналогичных выражений для
всех МТ, входящих в систему
i=1,2,…,n, получаем
t
n
n
n
pi ( Fki )dt ( FBi )dt
i 1
0 i 1k 1
0 i 1
k i
n
t
34.
ЗАКОН ИЗМЕНЕНИЯ ПОЛНОГОИМПУЛЬСА СИСТЕМЫ
изменение полного импульса
системы равно импульсу
результирующей внешней
силы:
t
P F pBc dt
0
35.
dPF pBc
dt
действующая на систему
результирующая внешняя сила
равна изменению полного
импульса системы за единицу
времени
36.
ЦЕНТР МАСС СИСТЕМЫ– это такая условная точка
пространства, радиус-вектор
которой определяется по
формуле:
Rцм
n
1
mi ri
М i 1
37.
Иными словами ЦМС – этоточка с координатами
1 n
1 n
1 n
X цм
mi xi ; Yцм
mi yi ; Z цм
mi z i ,
M i 1
M i 1
M i 1
где M=m1+m2+…+mn - полная масса
всей системы
38.
ЦМСобладает рядом интересных
свойств
n
n
dRцм
dri d n
d 1 n
P pi mi
( mi ri ) M ( mi ri ) M
Mvцм ,
dt dt i 1
dt M i 1
dt
i 1
i 1
Система МТ, как целое, подчиняется уравнению,
аналогичному второму закону Ньютона:
Maцм FpBc
39.
ТЕОРЕМА О ДВИЖЕНИИЦЕНТРА МАСС
ЦМС движется так, как
двигалась бы МТ с массой
равной массе всей системы, и
если бы все внешние силы
были приложены к этой точке
40.
ЗАКОН СОХРАНЕНИЯИМПУЛЬСА
В замкнутой (изолированной)
механической системе полный
импульс сохраняется
P const
m1v1 m 2 v 2 ... m n v n m1u m 2 u 2 ... m n u n
41.
Вопрос 7.ОСНОВНЫЕ ПОЛОЖЕНИЯ
СТАТИКИ
42.
Законы сложения иразложения сил, а также
условия их равновесия
изучаются в разделе
механики, называемой
СТАТИКОЙ
43.
РЕЗУЛЬТИРУЮЩЕЙ (илиравнодействующей)
двух
или
более сил F1, F2 ,..., Fn ,
приложенных к телу, называется
такая сила F рс , результат
действия которой на тело
оказывается таким же, как и
результат совокупного действия
всех этих сил
44.
ОСНОВНЫЕ ПОЛОЖЕНИЯСТАТИКИ
1. Силу, приложенную к абсолютно
твёрдому телу, можно перемещать
вдоль линии её действия.
2.
Результирующая
сил,
приложенных в одной точке, равна их
векторной сумме:
F рс F1 F2 ... Fn.
45.
ПРАВИЛО ПАРАЛЛЕЛОГРАММА46.
ОСНОВНЫЕ ПОЛОЖЕНИЯСТАТИКИ
3.
Всякая
сила
может
быть
разложена на составляющие вдоль
любых двух прямых линий.
47.
48.
Вопрос 8.ДИНАМИКА
МАТЕРИАЛЬНОЙ ТОЧКИ,
ДВИЖУЩЕЙСЯ ПО
ОКРУЖНОСТИ
49.
МЕХАНИЧЕСКИЙМОМЕНТ СИЛЫ
M r F
M F r sin Fк r F l
l r sin
Fк F sin
50.
Для динамического описания движения МТпо окружности под действием силы
применим второй закон Ньютона в
проекциях на касательное направление:
ma к Fк
Умножая это уравнение на радиус r
окружности, получаем
mr M
2
51.
МОМЕНТ ИНЕРЦИИ МТI mr
2
ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ
для движения МТ по окружности
В ФОРМЕ ВТОРОГО ЗАКОНА
НЬЮТОНА:
I M
52.
МОМЕНТ ИМПУЛЬСАЭто векторная физическая
величина, равная векторному
r
произведению радиус-вектора
и
импульса p mv МТ
L r p
L I
L pr mvr
L mvr m r I
2
53.
ОсновноеУРАВНЕНИЕ ДИНАМИКИ
движения МТ по окружности
в ФОРМЕ МОМЕНТОВ:
d
I
M
dt
d ( I )
I mr const ,
M
dt
2
dL
M
dt
54.
Вопрос 9.ДИНАМИКА
ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО
ТЕЛА С НЕПОДВИЖНОЙ
ОСЬЮ ВРАЩЕНИЯ
55.
АБСОЛЮТНО ТВЕРДЫМТЕЛОМ (АТТ)
называется такое тело,
которое не испытывает
деформации под
воздействием приложенных
сил
56.
I i M ;dL
Mi
dt
I i mi ri
n
d n
Ii M i ;
( Li ) M i
dt
i 1
i 1
i 1
i 1
n
n
2
57.
МОМЕНТ ВНЕШНИХ СИЛn
n
( внутр.)
( внешн.)
Mi
0 M вс M вс
Mi Mi
i 1
i 1
i 1
n
n
( внешн.)
M вс M i
i 1
58.
МОМЕНТ ИНЕРЦИИ ТЕЛАn
n
i 1
i 1
I I i mi ri
I r dm ( r ) r dV
2
(m)
(V )
n
lim
2
( ri )ri Vi
( Vi 0i 1
n )
2
59.
60.
61.
МОМЕНТ ИМПУЛЬСА ТЕЛАn
n
n
L Li I i I i I
i 1
i 1
i 1
62.
ОСНОВНОЕ УРАВНЕНИЕДИНАМИКИ вращающегося АТТ
В форме второго закона Ньютона
произведение момента инерции на угловое
ускорение равно вращающему
механическому моменту внешних сил
I M вс
63.
ОСНОВНОЕ УРАВНЕНИЕДИНАМИКИ вращающегося АТТ
В форме уравнения моментов
изменение момента импульса тела за
единицу времени равно полному
механическому моменту внешних сил
dL
M вс
dt






















































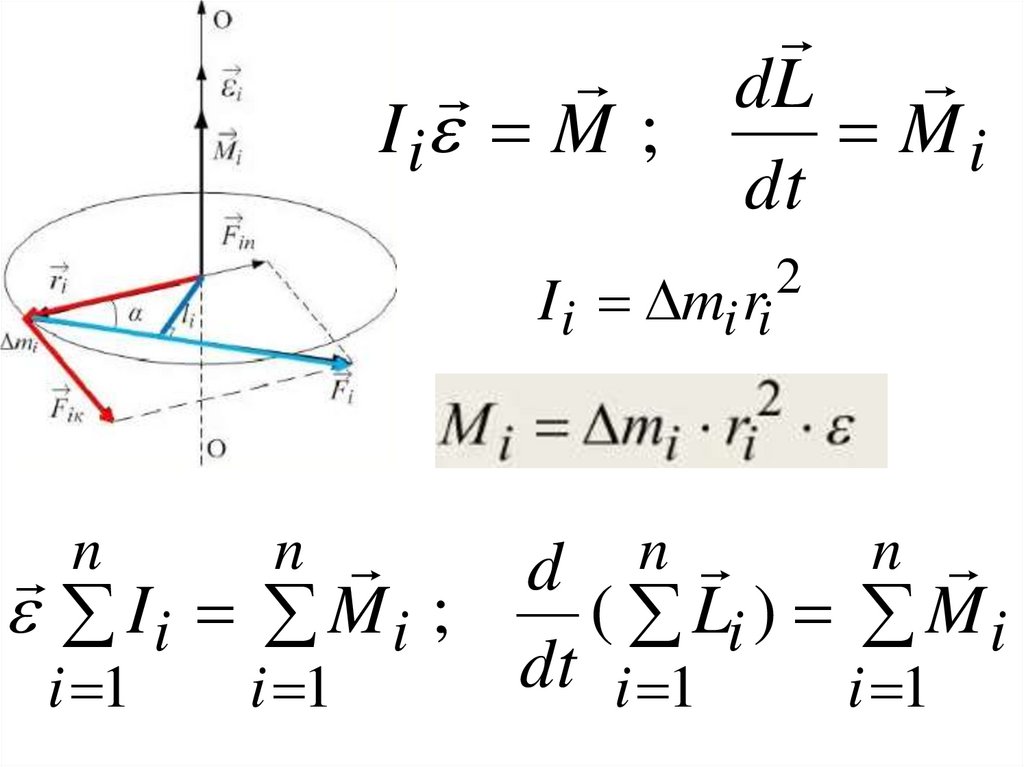








 physics
physics








