Similar presentations:
Учебное пособие для углубленного изучения математики в 7-м классе
1.
Федеральное агентство по образованиюНациональный исследовательский ядерный университет «МИФИ»
Т.А. Пыжова, Г.В. Лупенко, И.А. Масленникова
МАТЕМАТИКА
Учебное пособие
для углубленного изучения математики в 7-м классе
Москва 2009
2.
УДК 51(075)ББК 22.127
П 94
Пыжова Т.А., Лупенко Т.В., Масленникова И.А. Математика: Учебное пособие для углубленного изучения математики в 7-м классе. М.: МИФИ, 2009. – 76 с.
Даны примеры задач по алгебре и геометрии для 7-го класса.
Задачи систематизированы по темам и снабжены ответами.
Пособие предназначено учащимся, которые готовятся поступать в 8-е классы
вечерних лицеев при МИФИ, а также учителям, организующим эту подготовку.
Авторы:
Пыжова Т.А., кандидат технических наук, доцент МИФИ, почетный работник
«Высшего образования РФ»;
Лупенко Г.В., кандидат физико-математических наук, доцент МИФИ, соросовский учитель, почетный работник «Высшего образования РФ»;
Масленникова И.А., соросовский учитель, заслуженный учитель РФ.
Рецензент канд. физ.-мат. наук, доц. А.Н. Рурукин
ISBN 978-5-7262-1051-3
© Национальный исследовательский
ядерный университет «МИФИ», 2009
3.
СодержаниеТребованияк математической подготовке учащихся ...................4
Алгебра
Примеры и задачи ..................................................................................5
Раздел I. Арифметические примеры ...............................................5
Раздел II. Признаки делимости ........................................................8
Раздел III. Проценты .........................................................................9
Раздел IV. Пропорции.....................................................................10
Раздел V. Уравнения .......................................................................11
Раздел VI. Текстовые задачи..........................................................19
Раздел VII. Степени ........................................................................24
Раздел VIII. Одночлены, многочлены. Разложение
многочленов на множители ...........................................................27
Раздел IX. Понятие о функции и графике функции ....................28
Раздел X. Системы уравнений .......................................................33
Ответы ...................................................................................................37
Геометрия
Справочник по геометрии ...................................................................46
Задачи ....................................................................................................50
Раздел I. Смежные и вертикальные углы .....................................50
Раздел II. Равенство треугольников. Сумма углов
треугольника....................................................................................51
Раздел III. Равнобедренные треугольники....................................53
Раздел IV. Призники и свойства параллельных прямых .............55
Раздел V. Окружность ....................................................................57
Раздел VI. Задачи на построение ...................................................58
Раздел VII. Задачи на повторение .................................................59
Ответы ...................................................................................................61
3
4.
ТРЕБОВАНИЯ К МАТЕМАТИЧЕСКОЙ ПОДГОТОВКЕУЧАЩИХСЯ
Для успешной сдачи письменного экзамена по математике учащиеся должны хорошо владеть знаниями и умениями по следующим разделам.
1. Натуральные числа и их свойства. Делимость чисел. Признаки делимости на 2, 3, 4, 5, 9, 10, 100 и т. д. Разложение числа на
простые множители. Учащиеся должны владеть понятиями, связанными с делимостью чисел, на уровне, позволяющем использовать их при решении широкого круга задач.
2. Решение задач на все действия с обыкновенными и десятичными дробями. Учащиеся должны владеть достаточно развитой
техникой вычисления с рациональными числами: бегло и уверенно
выполнять арифметические действия письменно, владеть навыками
устных вычислений, а также уметь применять приемы, упрощающие вычисления.
3. Решение задач на проценты. Нахождение процента от числа.
Нахождение числа по процентам от него. Нахождение процентного
отношения двух чисел.
4. Модуль числа. Решение простейших уравнений, содержащих
модуль.
5. Отношение двух чисел. Нахождение числа по его части. Пропорция. Свойства пропорции. Деление числа в данном отношении.
Решение задач на пропорциональное деление.
6. Решение линейных уравнений и их систем. Решение линейных уравнений, содержащих параметр. Исследование систем линейных уравнений.
7. Решение текстовых задач. Анализ полученных результатов.
8. Понятие функции и ее графика. Учащиеся должны понимать
содержательный смысл важнейших свойств функций; находить
значения функций, заданных формулой, таблицей, графиком, решать обратную задачу; уметь строить и читать график линейной
функции.
9. Многочлен. Равенство многочленов. Действия с многочленами. Формулы сокращенного умножения. Методы разложения многочленов на множители. Представление о методе неопределенных
коэффициентов.
10. Понятие степени с натуральным показателем. Действия со
степенями.
11. Решение геометрических задач. Учащиеся должны уметь
выполнять чертежи по условию задачи, вычислять значения геометрических величин (длин, углов), применяя изученные свойства
и формулы, проводить аргументацию в ходе решения задач.
Настоящее пособие не заменяет школьного учебника, а только
дополняет его и углубляет.
4
5.
АЛГЕБРАПримеры и задачи
Раздел I. Арифметические примеры
Выполнить действия.
⎛ 1
⎞
1. ⎜1 ⋅ 2,6 − 4 ⎟ : 1,2 + 0,3 .
⎝ 4
⎠
2. 0,25 +
9⎞
1 ⎛1
: ⎜ ⋅ 1,25 − ⎟ .
12 ⎝ 3
16 ⎠
2
: 0,8 − 0,5
9
3.
.
1,6 ⋅ 0,25
3 ⎛ 1 2⎞ ⎛ 3 5⎞ 1
2 : ⎜1 − ⎟ + ⎜ + ⎟ : 3
4 ⎝ 2 5⎠ ⎝ 4 6⎠ 6
4.
.
2 1⎞ 4
⎛ 1 2
+
⋅
3
:
4
4
:
3
4
⎜
⎟
3 2⎠ 5
⎝ 2 3
7 ⎞ 30 ⎛
1⎞ 5
⎛2
− ⎜2 : 2 ⎟ ⋅
⎜ + ⎟⋅
15 12 ⎠ 43 ⎝
2 ⎠ 32
5. ⎝
.
5
21
2
⎞
⎛
⎜11 − 8 ⎟ : 1
22 ⎠ 3
⎝ 11
3 5
1 2
1
: + 2 ⋅ − 1:1
4
6
2
5
6.
6.
3
⎛⎛ 1 ⎞ 3 ⎞ 7
⎜ ⎜1 ⎟ − ⎟ :
⎜⎝ 2 ⎠ 4 ⎟ 8
⎝
⎠
7. 227,36 : (865,6 − 20,8 ⋅ 40,5) ⋅ 8,38 + 1,12 .
5
6.
8. 275,4 : (22,74 + 9,66) ⋅ (937,7 − 30,6 ⋅ 30,5) .3
⎛2 5 5 ⎞
⎜ ⋅ : ⎟
⎝ 7 12 14 ⎠
9.
.
4 3
4
1
12 ⋅ 3 − 4 ⋅ 4
5 4
11 8
2 7
11 :
3 18
2
⎛ ⎛ 2 ⎞2 ⎛ 4 ⎞2 ⎞
⎜⎜ ⎟ :⎜ ⎟ ⎟
⎜ 3
9 ⎟
10. ⎜ ⎝ ⎠ ⎝ 2⎠ ⎟ .
⎜ ⎛⎜ 2 : 4 ⎞⎟ ⎟
⎟
⎜ 3 9
⎠ ⎠
⎝ ⎝
11. (2 − 5 + 7 − 1)2 : (−3) 2 − 21 .
1
12. (8 − 11 + 5 − 5)3 : ( −2) 2 + 3 .
2
13. 1,7 ⋅ 100 : 0,1 ⋅ 0,0001 : 10 : 0,01 .
1⎞
⎛
14. ⎜1,52 − 2,1 ⋅ 1 ⎟ : 1,2 .
2⎠
⎝
⎛ 1
⎞ 1
15. ⎜1 ⋅ 0,7 − 1,2 2 ⎟ : 1 .
⎝ 5
⎠ 2
7 4 3⎞
⎛
⎜ 0,5 : 1,25 + : 1 − ⎟ ⋅ 3
5 7 11 ⎠
16. ⎝
.
1⎞
1
⎛
⎜1,5 + ⎟ : 18
4⎠
3
⎝
6
7.
1⎛
⎞
⎜ (2,7 − 0,8) ⋅ 2
⎟
3 + 0,125 ⎟ : 2 1 + 0,43 .
17. ⎜
⎜ (5,2 − 1,4) : 3
⎟ 2
⎜
⎟
70
⎝
⎠
1 ⎞ ⎛1
1⎞
⎛1
⎜ + 0,1 + ⎟ : ⎜ + 0,1 − ⎟ ⋅ 2,52
6
15 ⎠ ⎝ 6
15 ⎠
18. ⎝
.
1
1⎞ ⎛
1⎞ 7
⎛
⎜ 0,5 − + 0,25 − ⎟ : ⎜ 0,25 − ⎟ ⋅
3
5⎠ ⎝
6 ⎠ 13
⎝
1
⎛ 1
⎞ ⎛
⎞
⎜ 3 + 2,5 4,6 − 2
⎟ ⎜ 0,05
⎟
3
3
19. ⎜
⋅
⋅ 5,2 ⎟ : ⎜
+ 5,7 ⎟ .
⎜ 2,5 − 1 1 4,6 + 2 1
⎟ ⎜ 1 − 0,125
⎟
⎜
⎟ ⎜
⎟
3
3
⎝
⎠ ⎝7
⎠
20.
(7 − 6,35) : 6,5 + 9,9
5 ⎞ 169
⎛
⎜1,2 : 36 + 1,2 : 0,25 − 1 ⎟ :
16 ⎠ 24
⎝
.
5
: 0,4 − 1,5
21. 9
.
0,008 ⋅ 12,5
1 ⎛
3 ⎞ 1 ⎛ 1 23 ⎞ 22
3,75 : 1 + ⎜1,5 : 3 ⎟ ⋅ 2 + ⎜1 − ⎟ :
2 ⎝
4 ⎠ 2 ⎝ 7 49 ⎠ 147 .
22.
1 ⎛ 1
⎞ 2 ⎛ 5 17 ⎞ 18
2 : 3 + ⎜ 3 : 13 ⎟ : − ⎜ 2 − ⎟ ⋅
5 ⎝ 4
⎠ 3 ⎝ 18 36 ⎠ 65
⎛⎛ 7
11
1 ⎞ 5
3 ⎛ 1 5 ⎞⎞ 7
⎜⎜ ⎜ 3 − 2 + 2 ⎟ ⋅ 1 − ⎜ 3 + ⎟ ⎟⎟ ⋅ 1
12
18
24
31
52
⎠
⎝ 2 6 ⎠ ⎠ 13
23. ⎝ ⎝
.
13 5 ⎞
2 1 4
19 ⎛ 13
: ⎜5 − 2 + ⎟ +1 − ⋅
84 ⎝ 42
28 24 ⎠ 27 3 9
7
8.
Вычислить наиболее удобным способом (без использованиямикрокалькулятора).
24.
25.
3,52 − 2,52
.
0,8 ⋅ 0,6 − 0,6
1,6 ⋅ 0,4 − 0,4
2
1,4 − 2,6
2
26.
.
27.
0,2 ⋅ 1,8 + 0,8 ⋅ 1,8
1,32 − 0,52
.
0,2 ⋅ 0,6 − 0,2 ⋅ 1,6
12 − 0,82
.
3
4
⎛ 13
⎞
28. ⎜ 3 − 12 − 5 − 0,85 ⎟ ⋅ 3 .
15
20
45
⎝
⎠
29.
832 + 2 ⋅ 83 ⋅ 17 + 17 2
832 − 17 2
.
3
4⎞ ⎛
1⎞
⎛
30. ⎜ − 5,17 : 1 + 1,67 ⋅ ⎟ ⋅ ⎜ − 1 ⎟ .
4
7 ⎠ ⎝ 11 ⎠
⎝
5
4⎞
⎛
31. ⎜ 7,52 ⋅ − (− 11,48) : 1 ⎟ : 0,38 .
9
5⎠
⎝
Раздел II. Признаки делимости
Основные признаки делимости натуральных чисел:
Число делится на 2, если последняя цифра этого числа — четная;
Число делится на 3, если сумма цифр этого числа делится на 3;
Число делится на 4, если две последние цифры его образуют
число, которое делится на 4;
Число делится на 5, если его последняя цифра — 0 или 5;
Число делится на 8, если три его последние цифры образуют
число, которое делится на 8;
Число делится на 9, если сумма цифр этого числа делится на 9;
Число делится на 10, если его последняя цифра — 0;
8
9.
Число делится на 11, если разность сумм цифр числа, стоящихна четных и нечетных местах кратно 11.
1. Какие цифры можно поставить вместо звездочки, чтобы число делилось без остатка на 3 и на 5 одновременно:
1) 241*; 3) 43*5; 2) 1734*; 4) 43*0?
2. Определить, делится ли число 1234067895 без остатка на 45?
3. Вставить в числе 222...22 ∗ 5 цифру вместо звездочки, чтобы
13 цифр
число делилось на 75 .
4. Какую цифру нужно поставить вместо звездочки в число
*137812, чтобы вновь полученное число делилось на 6?
5. Является ли число 71634453 простым или составным?
6. К числу 111…11 допишите по одной цифре слева и справа
15 цифр
так, чтобы вновь полученное число делилось на 45. Найти все возможные варианты.
7. Дано число — 7453*41. Определить число сотен, если число
делится на 9.
8. Известно, что число 173913871* делится на 12 без остатка.
Определить цифру *?
9. Определить число десятков, если число 7359917383*6 делится
на 8 без остатка. Рассмотреть все возможные варианты.
10. Определить, делятся ли числа 1892 и 5280 на 11?
Раздел III. Проценты
Процентом называют одну сотую часть числа. Чтобы перевести
проценты в десятичную дробь, надо разделить число процентов
на 100.
1. Найти:
а) 1,5 % от 40; б) 3 % от 60; в) 15 % от 500.
2. Чему равно число:
а) 3 % которого равны 63; б) 8 % которого равны 48; в) 25 % которого равны 125?
3. Сколько процентов составляет число:
а) 26 от числа 200; б) 5 от числа 100; в) 29 от числа 500?
4. 3 % от вклада составляет 150 руб. Какова величина вклада?
9
10.
5. Каков процент жирности молока, если в 1 кг его содержится45 г жира?
6. По вкладам начисляется ежегодно 2 % от вклада. В банк внесли 150 руб. Какой станет сумма вклада через два года?
7. Что больше: 20 % от 10 % данного числа или 10 % от его
20 %?
Раздел IV. Пропорции
Равенство двух отношений называют пропорцией. Основное
свойство пропорции: в верной пропорции произведение крайних
членов равно произведению средних.
Решить пропорции.
3 1
1
1. 5 : 3 = 5 : X .
4
5 2
6.
5
10
=
.
6 2x − 3
1
1 1
2. y : 3 = 4 : 2 .
2 4
5
7.
2x −1 1
= .
3
2
8.
6
2
= .
3x + 2 5
3. 0,2 : ( x − 2 ) =
1 1
:2 .
2 2
2
7
4. 2 : 0,24 = 1 : (x + 0,06 ) .
3
9
1
6 = 1,12 .
9.
8
X
0,3 +
15
4
2
5.
= .
3+ x 3
3
3
6 −3
5
14 = X .
10.
(21 − 1,25) : 2,5 5 5
6
0,75 −
10
11.
11: 12,5
5
7
11.
.
=
1
2
2 − 1,2 18 ⋅ ⎛⎜ X − 4 ⎞⎟
7
3⎠
⎝
14.
5
9
1
+
2,5 +
4
20
3.
=
12.
23 − X
21,25
15. y :
7 5⎞ 2
⎛
⎜ 2 + − ⎟: 2
30 18 ⎠ 3 3 X − 2
13. ⎝
=
.
0,04
3
11 − 9,5 0,6 ⋅ 35
=
.
3,75 + X
87,5
3
1 4
=3 : .
9 9
14
2
16.
2
3
X +
1
3
=
1
1
2
X −1
1
8
.
⎛
1 ⎞⎞
⎛ 1
2 3 1
⎜⎜ 4 − 3,5 ⋅ ⎜ 2 − 1 ⎟ ⎟⎟ : 0,16
3 − :
7
5
⎝
⎠⎠
17. ⎝
= 7 14 6 .
23
49
x
41 − 40
84
60
⎛ 28 17 ⎞
⎜1 − ⎟ ⋅ 0,7
0,125 x
63 21 ⎠
18.
= ⎝
.
19
21
7
0,675 ⋅ 2,4 − 0,02
⎛
⎞
− ⎟ ⋅8
⎜
⎝ 24 40 ⎠ 16
Раздел V. Уравнения
Равенство, которое содержит неизвестное число, обозначенное
буквой, называется уравнением.
Корнем уравнения называется то значение неизвестного, при
котором это уравнение обращается в верное равенство.
Решить уравнение — значит найти все его корни или установить, что их нет.
Выражение вида ax + b = 0 называется линейным уравнением,
где a и b — некоторые числа; x — переменная.
11
12.
Основные свойства уравнений:• к обеим частям уравнения можно прибавить или вычесть одно
и то же число;
• любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный;
• обе части уравнения можно умножить или разделить на одно и
то же число, не равное нулю.
Решить уравнения.
I тип уравнений (преобразование уравнений)
1
1 1
1. 2 a = 4 ⋅ 1 .
2 9
3
2. 8
1
2 1
z = 3 ⋅1 .
2
3 11
3. 5 (x + 7) = 3 (2x – 3).
4. 0,2 (x – 2) = 0,7 (x + 3).
5. 2 (x + 3) – 3 (x + 2) = 5 – 4 (x + 1).
6. 3 (x – 2) – 2 (x – 1) = 17.
7. 3 – 5 (x – 1) = x – 2.
8. 11 (y – 4) + 10 (5 – 3y) – 3 (4 – 3y) = – 6.
9. 2 (x + 1) – 1 = 3 – (1 – 2x).
10. 6 (1,2x – 0,5) – 1,3x = 5,9x – 3.
11. 8 (1,3x + 0,25) – 6,6x = 3,8x + 2.
12. 25x – 17 = 4x – 5 – 13x + 14 + 34x.
13. 7 (–12 + y) –5(–18 + y) = 6.
14. (x + 3) 6 = (x + 1) 9.
12
13.
15. 3 (y + 7) – 4(y + 4) = 0.16. –3,2a + 4,8 = –2 (1,2a + 2,4).
17. –5 (0,8y – 1,2) = –y + 7,2.
18. 13x (6x – 1) + 24x = –13 – 6x (9 – 13x).
19. 5y (12y + 7) – 29y = 30 + 4y (15y – 11).
20. 7x (6x – 5) + 42x = 3x (5 + 14x) + 49.
1
5⎛
3
⎞
21. 1 + 1 ⎜ X : 1,8 − ⋅ 2,02 ⎟ = − 2,5 .
6
6⎝
2
⎠
⎛
5
⎛ 2
⎞⎞ 8
22. ⎜⎜1,7 : ⎜1 X − 3,75 ⎟ ⎟⎟ :
=1 .
12
⎝ 3
⎠ ⎠ 85
⎝
⎛ 55
⎞ 15 1 8
23. ⎜ : X + 1,5 ⎟ ⋅
= +
.
⎝ 84
⎠ 37 3 21
17 ⎞ ⎛ 5 ⎞
1
⎛ 11
24. ⎜1 X − 1 ⎟ : ⎜ ⎟ 2 = 0,25 −
.
18 ⎠ ⎝ 6 ⎠
20
⎝ 39
5⎞
1
3
⎛ 7
25. ⎜ 2 − ⎟ : 18 = 5 X −
.
6
20
⎝ 30 12 ⎠
⎛
1⎛ 2
2
⎞⎞ 4
26. 0,9 ⎜⎜ 3 : 2,25 − ⎜1 + X ⎟ ⎟⎟ − : 0,8 = .
8
3
7
7
⎝
⎠⎠
⎝
II тип уравнений (преобразование уравнений и разложение на
множители; применение формул сокращенного умножения)
1. –5х2 + 6х = 0.
2. 8у2 – у = 0.
3. (х2 - х) (2x + 1) (3x + 5) = 0.
13
14.
4. (9x – 3) (5x + 2) (x2 + 4х) = 0 .5. (5х – 7) (8х + 1) = (7 – 5х) .
6. (х – 1) (2х + 1) + (х – 1) = (х + 1) (х – 1) .
7. (2 – 3х) (х + 1) – (3х – 2) (3х + 1) = 0 .
8. (4х – 1) (5х + 7) – (1 – 4х) + (4х – 1) (3х + 2) = 0 .
9. (5у2 + у) (3у – 1) + 2(у + 5у2) = 0 .
10. (7 y − 5) − ( y − 8) (5 − 7 y ) + (7 y − 5) (3 y + 1) = 0 .
11. (4а – 1) + (1 – 4а) (3а +1) = (1 – 4а) .
12. y + 4 − y ( y + 4) = 0 .
13. (x − 6)2 − 2 x + 12 = 0 .
14. 5 y − 5 − ( y − 1)2 + 1 − y = 0 .
15. (x − 2)2 + 3x − 6 − 5(2 − x) = 0 .
16. − 2(5 − 3 x ) = (3 x − 5) 2 .
17. 2 x − 14 + 5(7 − x ) = (7 − x ) 2 .
18. x 2 ( x − 8) − 3 x ( x − 8) 2 = 0 .
19. 4х2 – 9 = 0 .
20. 1 – 4у2 = 0 .
21. 2а2 – 8 = 0 .
22. (х2 + 2х + 1) + (х + 1) (3х –1) = 0 .
23. х3 – 5х2 – 4х + 20 = 0 .
24. 4 y − 6 = 4 y 2 − 9 .
14
15.
25. (5 x + 4) (3 x − 2) = 9 x 2 − 12 x + 4 .26. ( x − 1) (3 x + 5) = 1 − x 2 .
27. 3 x + 6 = x 2 − 4 .
(
)
28. (3 x + 1) (5 x − 3) + 9 x 2 + 6 x + 1 = 0 .
29. ( 2 x − 1) (8 x + 1) = −4 x 2 + 4 x − 1 .
30. (3 x − 1) (8 x + 5) = −18 x 2 + 12 x − 2 .
31. (7 x − 1) (3 x + 5) = 9 x 2 + 30 x + 25 .
32. ( 2 x + 3) (3 x − 7) = 49 − 9 x 2 .
33. (3 x + 2) (5 x − 9) = 27 x 2 − 12 .
34. (8 x − 1) ( x − 2) = 5 x 2 − 20 x + 20 .
35. (3 x + 1) (7 x + 5) = 1 − 9 x 2 .
36. ( x − 1) (8 x + 3) = −3 x 2 + 6 x − 3 .
37. ( 2 x − 3) (7 x + 2) = 8 x 2 − 24 x + 18 .
38. ( x − 3) ( 2 x + 5) = 25 − 4 x 2 .
39. (11 y − 7 ) (1 − 8 y ) = 256 y 2 − 4 .
40. (9 z + 1) (1 − 5 z ) = 162 z 2 − 2 .
41. 49 x 2 − 25 = (5 − 7 x ) (3 x − 2) .
42. 0,25 − x 2 = ( x − 0,5) ( 2 x + 0,7 ) .
43. 0,64 − x 2 = (3 x − 7) ( x − 0,8) .
15
16.
44. 0,81 = ( 2 x − 0,9) (3x − 5) + 4 x 2 .45. 0,36 x 2 − 49 = (6 x − 7) (7 − 0,6 x ) .
46. 64 x 2 − 48 x + 9 = (3 − 8 x ) (3 x − 8) .
47. x 2 − 4 x + 4 = x − 2 .
III тип уравнений (приведение уравнений к общему знаменателю)
1. 7 −
x
7x
=3+
.
2
2
2. 9 −
2x
x
=7+ .
3
3
3.
5x 1 − 3x
x−7
−
=x−
− 1.
6
5
15
4.
2x − 3 3 − 4 x 3 − 5x
−
−
= 0.
2
4
8
5.
4 x − 3 5 − 2 x 3x − 4
−
=
.
2
3
3
6.
x − 1 5 x + 2 5 + 3x
+
=
.
3
12
4
7.
5x x − 3
x−5
−
=1+
.
2
3
6
3 ⎞
⎛
8. 8 ⎜11 − z ⎟ = 16 z − 44 .
4 ⎠
⎝
9.
(
)
x(x − 1) 2 x 2 + 1 ( x − 1) (x + 2 )
−
=
.
7
28
14
16
17.
10.(x − 2)2
5
+
2 x 2 − 3 ( x − 1) ( x + 1)
=
.
15
3
11.
4x − 3 5 − 2x 4x − 7
−
−
= 0.
2
3
6
12.
2x − 3 3 − 4x 3 − 5x
−
−
= 0.
2
4
8
IV тип уравнений (уравнения с модулем)
Модуль положительного числа равен самому числу.
Модуль отрицательного числа равен противоположному ему
числу.
⎧ a, если a ≥ 0 ;
Если модуль обозначен буквой, то a = ⎨
⎩− a, если a < 0.
Модуль нуля равен нулю: 0 = 0 .
Если модуль записан от выражения, содержащего букву, то следует рассматривать два случая:
• когда выражение, стоящее под знаком модуля больше или равно нулю, то знак модуля можно опустить;
• когда выражение под знаком модуля меньше нуля, то при снятии знака модуля следует умножить все выражение на минус единицу.
1.
x + 10 = 7 .
8. 3 x = 0,09 .
2. 3 + 2 x = 2 − 3x .
9.
3. 14 = 7 x + 1 .
10.
x = 1.
2 x = 0,16 .
2x − 1 = 7 .
11. 7 − 4 2 x + 1 = 3 .
5. 2 x − 1 + 1 = 9 .
12. 6 + 5 x = 5 − 6 x .
6.
x − 11 = 1 .
13. 5 + 3 x = 3 − 5 x .
7.
x −1 = x + 3 .
4.
17
18.
V тип уравнений (уравнения в целых числах)1. y (x + 1) = 3 .
3. 2у – 3ху = 5 .
2. ху – у = 6 .
4. ху – 6 = – х .
5. Пусть число имеет a-десятков и b-единиц. Известно, что число в
5 раз больше суммы цифр. Найдите числа а и b.
6. xy + x = 8 .
7. 2x – xy = 4 .
8. 3y + 2xy = 5 .
VI тип уравнений (уравнения с параметрами)
Уравнение, содержащее кроме цифр и неизвестного еще величину, обозначенную буквой, будем называть уравнением с параметром.
Для решения уравнений такого типа необходимо сначала найти
неизвестное, считая параметр (букву) как некоторое число, а затем
исследовать полученный результат на наличие решений в зависимости от параметра. Методы решения заданий такого типа достаточно разнообразны: либо проводится перебор всех возможных
вариантов, либо используются графические представления, а затем
проводится анализ полученных графиков. В данном пособии рассмотрены простейшие варианты уравнений с параметрами.
Определить, при каких значениях а уравнение имеет решение.
1.
1 − 3x
= 1.
a
5. 5 − 2ax = 2 (7 + x) .
2.
2x − a
= 3.
8
6.
8 − 3ax 8 − ax
=
.
2
6
3. 8 = ax − 3a .
7. 7ax − 56 x + 5 = 0 .
4. (a − 2) x + 5 = 11.
8. 3ax + 21x − 7 = 0 .
18
19.
()
3 (3ax − 1) x a 2 + 2a
.
=
7
2
2 (7 ax + 4) ax ( a + 3)
=
.
12.
5
2
8 − ( a + 4) x 5 + ax
=
.
7
3
3 x − ( a − 2) x 7 + ax
=
.
10.
3
2
9.
11.
При каких значениях a уравнение не имеет решений?
13. 6a 2 x − 48ax − 7 = 0 .
Раздел VI. Текстовые задачи
I тип (общего типа)
1. В трех поселках 6 000 жителей. Во втором поселке вдвое
больше жителей, чем в первом, а в третьем — на 400 жителей
меньше, чем во втором. Сколько жителей во втором поселке?
2. В одном элеваторе было зерна в 2 раза больше, чем в другом.
Из первого элеватора вывезли 750 т зерна, на второй элеватор привезли 350 т, после чего в обоих элеваторах стало поровну. Сколько
зерна было первоначально в каждом элеваторе?
3. В трех коробках находится 119 карандашей. В первой коробке
на 4 карандаша больше, чем во второй, и на 3 карандаша меньше,
чем в третьей. Сколько карандашей в каждой коробке?
4. Отцу 30 лет, а сыну 4 года. Через сколько лет отец будет
втрое старше сына?
5. В треугольнике первый угол больше второго в 2 раза, а третий
угол больше второго на 40°. Чему равны углы треугольника?
6. Бригада должна была выполнить заказ за 10 дней. Ежедневно
перевыполняя норму на 27 деталей, бригада за 7 дней работы не
только выполнила задание, но еще изготовила дополнительно
54 детали. Сколько деталей в день изготовляла бригада?
7. Одно число больше другого в 1,5 раза, среднее арифметическое этих двух чисел равно 30. Найти эти числа.
8. Первое число в 2,4 раза больше третьего, а второе число на
0,6 больше третьего числа. Найдите эти три числа, если их среднее
арифметическое равно 2,4.
19
20.
9. Второе число на 0,8 больше первого, а третье в 3,2 раза больше первого. Найдите эти три числа, если их среднее арифметическое равно 4,6.II тип (задачи на движение по реке)
1. За 6 ч катер проходит по течению на 20 км меньше, чем за
10 ч против течения. Какова скорость течения, если скорость катера в стоячей воде 15 км/ч.
2. Расстояние по реке между пунктами А и В равно 41 км. Из
пункта А в пункт В по течению плывет моторная лодка, собственная скорость которой равна 18 км/ч, а из В в А движется вторая
моторная лодка, собственная скорость которой равна 16 км/ч. При
встрече оказалось, что первая лодка плыла 1 ч, а вторая 1,5 ч. Найдите скорость течения реки.
3. Из двух пунктов реки, расстояние между которыми равно
80 км, одновременно навстречу друг другу вышли две моторные
лодки, собственные скорости которых равны. Через 2 ч они встретились. Найдите собственную скорость лодки, если скорость течения реки равна 4 км/ч.
4. Из двух пунктов реки одновременно навстречу друг другу
вышли две моторные лодки. Через 1,2 ч они встретились. Собственная скорость лодки, которая шла по течению реки, равна
18 км/ч, а лодка, которая шла против течения реки, имела скорость
16 км/ч. До встречи одна лодка прошла на 9,6 км больше другой.
Найдите скорость течения реки.
5. Из двух пунктов реки навстречу друг другу движутся две моторные лодки, собственные скорости которых равны. Скорость
течения реки равна 2 км/ч. До встречи лодка, идущая по течению,
шла 0,9 ч, а другая лодка шла 1 ч. Найдите собственную скорость
лодок, если лодка, идущая по течению, прошла на 2 км больше, чем
другая лодка.
III тип (задачи на движение)
1. Из двух аэропортов, расстояние между которыми равно
1300 км, вылетели одновременно навстречу друг другу два самолета: один — с поршневым, другой — с реактивным двигателем. Че20
21.
рез 30 мин им оставалось пролететь до встречи 800 км. Найдитескорость самолета с реактивным двигателем, если она в 3 раза
больше скорости самолета с поршневым двигателем.
2. Расстояние между двумя пунктами поезд проходит по расписанию с намеченной скоростью за 5 ч. Через 3 ч после отправления
он был задержан на 15 мин в пути. Поэтому, чтобы прибыть на
станцию назначения вовремя, поезд увеличил скорость на 10 км/ч.
Найдите первоначальную скорость поезда.
3. Из двух пунктов А и В, расстояние между которыми равно
10 км, одновременно в одном направлении выехали велосипедист и
мотоциклист, причем мотоциклист все время шел впереди велоси2
ч расстояние между ними было 30 км. Найдите
педиста. Через
3
скорость мотоциклиста, если известно, что она в 3 раза больше
скорости велосипедиста.
4. Сергей доехал на велосипеде от озера до деревни и вернулся
обратно, затратив на весь путь 1 ч. От озера до деревни он ехал со
скоростью 15 км/ч, а на обратном пути его скорость была 10 км/ч.
Чему равно расстояние от озера до деревни?
5. От города до поселка автомобиль доехал за 3 ч. Если бы он
увеличил скорость на 25 км/ч, то проехал бы это расстояние за 2 ч.
С какой скоростью ехал автомобиль и чему равно расстояние от
поселка до города?
6. Два пешехода вышли одновременно навстречу друг другу из
двух поселков и встретились через 3 ч. Расстояние между поселками 30 км. Найдите скорость каждого пешехода, если у одного она
на 2 км/ч меньше, чем у другого.
7. На первом участке пути поезд шел 2 ч со скоростью 60 км/ч, а
на втором он шел 3 ч. С какой скоростью шел поезд на втором участке, если его средняя скорость на двух участках была равна
51 км/ч?
8. Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч
по проселочной дороге со скоростью 30 км/ч. Найти среднюю скорость движения автомобиля на всем пути.
21
22.
IV тип (задачи на части и проценты)1. Две бригады лесорубов заготовили в январе 900 м3 древесины. В феврале первая бригада заготовила на 15 %, а вторая — на
12 % больше, чем в январе. Известно, что в феврале они заготовили
1020 м3 древесины. Сколько кубических метров древесины заготовила каждая бригада в январе?
2. Сумма двух чисел равна 400. Если первое число уменьшить
на 20 %, а второе на 15 %, то сумма полученных чисел уменьшится
на 68. Найдите значение чисел после их уменьшения.
3. Кооператив продавал пальто и куртки. Куртка стоила на
150 руб. дешевле пальто. На сезонной распродаже цена на куртки
была снижена на 20 %, а на пальто — 10 %, и теперь куртку и пальто можно купить за 645 руб. Сколько стоила куртка и пальто до
распродажи?
4. Смешали 1 г 13 %-го раствора соли и 1 г раствора той же соли
с неизвестным содержанием соли, получили 20 %-ный раствор.
Определить процентное содержание соли во втором растворе.
5. Рабочие отремонтировали дорогу длиной 820 м за 3 дня. Во
2
2
этой дороги, а в среду —
освторник они отремонтировали
5
3
тавшейся части. Сколько метров дороги отремонтировали рабочие
во вторник, среду, четверг?
3
5
6. Никита истратил
своих денег на покупку книги и
своих
7
14
денег на покупку альбома. Сколько денег было у Никиты, если
альбом дешевле книги на 7 руб.
V тип (задачи на составление системы уравнений)
1. Ученик за 3 общие тетради и 2 карандаша уплатил 66 руб.
Другой ученик за такие же 2 общие тетради и 2 карандаша уплатил
46 руб. Сколько стоила общая тетрадь и сколько стоил карандаш?
2. На туристической базе имеются палатки и домики; всего их
25. В каждом домике живут 4 человека, а в каждой палатке
2 человека. Сколько на туристической базе палаток и домиков,
если там отдыхает 70 человек?
22
23.
3. У причала находилось 6 лодок, часть из которых была 2местными, а часть 3-местными. Всего в эти лодки может поместиться 14 человек. Сколько 2-местных и сколько 3-местных лодокбыло у причала?
4. За 3 м одной ткани и за 3 м другой ткани заплатили 90 руб.
Сколько стоит 1 м каждой ткани, если 9 м первой стоят столько же,
сколько 6 м — второй?
5. По течению реки моторная лодка проходит 40 км за 2 ч, а
против течения проходит 35 км за 2 ч 30 мин. Найти скорость течения реки.
6. Для клуба приобрели 10 комплектов шахмат и 16 комплектов
шашек на сумму 11 000 руб. Сколько стоит один комплект шахмат
и один комплект шашек, если 4 комплекта шашек стоят на 220 руб.
дешевле, чем 3 комплекта шахмат?
7. За три пары лыж и четыре пары коньков уплатили 4 700 руб.
Сколько стоит пара лыж и сколько пара коньков, если две пары
коньков дороже одной пары лыж на 100 руб.?
VI тип (задачи на работу)
1. Две бригады, работая вместе, могут закончить уборку урожая
за 8 дней. Если первая бригада будет работать 3 дня, а вторая —
12 дней, то они выполнят 75 % всей работы. За сколько дней может
закончить уборку урожая каждая бригада, работая отдельно?
2. Бассейн наполняется одной трубой за а часов, другой — за
b часов. За сколько часов наполнится бассейн, если две трубы открыть одновременно?
3. Две машинистки, работая вместе, напечатали рукопись за
а часов. Одна из них могла бы выполнить эту работу за b часов. За
какое время могла бы напечатать рукопись другая машинистка?
VII тип (задачи повышенной сложности)
1. Длина садового участка на 10 м больше его ширины. Его
площадь решили увеличить на 400 м2. Для этого длину увеличили
на 10 м, а ширину — на 2 м. Найдите площадь нового участка.
23
24.
2. Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 меньше исходного. Найдите эти числа.3. Длина окружности переднего колеса кареты равна 3 м, а заднего — 4,5 м. Какое расстояние проехала карета, если переднее
колесо сделало на 20 оборотов больше заднего?
Раздел VII. Степени
Степенью числа a с натуральным показателем n , большим 1,
называется произведение n множителей, каждый из которых равен a :
a n = a ⋅ a ⋅… ⋅ a ,
n раз
где a — основание степени, n — показатель степени.
Степенью числа a с показателем 1 называется само число a :
a1 = a .
Свойства степеней:
a m ⋅ a n = a m+n ;
a m : a n = a m−n ,
(a ) = a
m n
mn
m > n, a ≠ 0 ;
;
(ab )n = a n b n ;
n
an
⎛a⎞
⎜ ⎟ = n;
b
⎝b⎠
b0 = 1 .
b ≠ 0;
24
25.
Вычислить.1.
( )
(5 ) ⋅ (5 ) ⋅ 5 .
5 2
2.
3.
10.
.
147
11.
625
39
12.
4.
(a ) ⋅ a ⋅ (b ) ⋅ b
(a ) ⋅ (b )
5.
(x ) ⋅ (x ) ⋅ x (b )
x ⋅ (x ) ⋅ b
2 3
5
3 3
5 2
2 2
2 7
2 2
2
2 3
7
5
14.
15.
11
3
5 3
2
(x ) ⋅ x ⋅ (x )
(x ) ⋅ x ⋅ (x ) ⋅ x
6 2
16.
3 7
3
4 3
5
.
17.
x2
9.
a 2 n −1 ⋅ a 5 ⋅ a 2 n
a ⋅ a 4 n +1
2
5n −1
⋅ c3
(z ) ⋅ z
.
.
( )
2 n +5
⋅ z0
25
.
z 2n ⋅ z 7
(x ) ⋅ (x ) ⋅ x
3 2
5
.
x 2n+3 ⋅ x 4
( )
3n ⋅ 2 2 n ⋅ 32 ⋅ 2 5
(2 ) ⋅ 2
n 2
3
⋅3
n +11
36 2 ⋅ 2 n +1 ⋅ 32n
2n ⋅ 9n
.
.
8
x13
10 2
8.
+b .
0
7 2
( )
6
0
(z ) ⋅ z ⋅ z − z .
z ⋅ (z ) ⋅ z
(x ) ⋅ (x ) ⋅ x ⋅ x
x ⋅ (x ) ⋅ x
.
2 3
7.
4 2
3
13.
.
⋅ b 3n
c 5n + 7 ⋅ c
2 n
7
2 3
7
3 11
6.
(c ) ⋅ c
3 2
.
3n − 2
b 6n ⋅ b 2
2 4
2 5
81 ⋅ 27 5
(b ) ⋅ b
2 3
4
210 ⋅ 7 2
( )
100 ⋅ 2 n ⋅ 52
n
2 n −2 ⋅ 52 n +1
( )
⋅ (5 ) ⋅ 3 ⋅ 5
15 n ⋅ 32 ⋅ 5 n +1
3n
.
2
n 3
( )
.
2
.
18.
25
147 ⋅ 7 n ⋅ 9 n ⋅ 32
32 n + 2 ⋅ 7 2 n +1
.
26.
(7 ) ⋅147 ⋅ 9 ⋅ 349 ⋅ 27 ⋅ (3 ) ⋅ 7
n 2
19.
n
n
5
2 n
3
.
( )
n
7
( )
⎛1⎞
3 ⎛ 1 ⎞
n 2 ⎛1⎞
2 3
n
⎜ ⎟ ⋅b ⋅⎜ 2 ⎟ ⋅ b ⋅⎜ ⎟ ⋅ b ⋅b
a
a
⎝ ⎠
⎝ ⎠
⎝a ⎠
.
20.
n +5
⎛1⎞
3 n +1
⎜ ⎟ ⋅b
⎝a⎠
( )
(0,7 )5 ⋅ 2n ⋅ 8 ⋅ ⎛⎜ 7 ⎞⎟
49
⎝ 10 ⎠ 100 .
n +1
2 ⋅ (0,7 )9
21.
22.
3
⋅
1,5n ⋅1,5n +3 ⋅ 23 ⋅ 1,5 2 ⋅ 2 2 n
1,52 n +3 ⋅ 2 2n +1
.
5
⎛1⎞
⋅ 2 ⋅ ⎜ ⎟ ⋅ 2 n+1
2
⎝ 3⎠
23. 3
.
1
2 n−1 ⋅
27
1
1 n 1 3
⋅2 ⋅ ⋅2
24. 8 4 4
.
⎛1⎞
n −1
⎜ ⎟ ⋅2
⎝2⎠
25.
26.
625 ⋅ (18)2 ⋅ 33 ⋅ 150
2
6
5 ⋅3 ⋅ 2
72 ⋅ 150 ⋅ 27
23 ⋅ 33 ⋅ 5
2
27.
.
28.
29.
.
26
28 ⋅ 98 ⋅ 75
7 3 ⋅ 20
.
49 ⋅ 32 ⋅ 300 ⋅ 125
21 ⋅ 2 6 ⋅ 54
18 2 ⋅ 93 ⋅ 12 2
15 2 ⋅ 28 ⋅ 310
.
.
27.
30.31.
32.
33.
( )
6 n ⋅ 2 2 ⋅ 3n + 2
27 n ⋅ 3n+5 ⋅ 2
3
.
n −1
34.
( )
⋅ 5 ⋅ (2 ) ⋅ 3 ⋅ 2
8 k ⋅ 27 k ⋅ 5k +1
25 k
k −1 2
75 ⋅ 52 ⋅ 4 2 ⋅ 33
34 ⋅ 2 2 ⋅ 53
150 ⋅ 75 ⋅ 16 ⋅ 27
( )
2
25 ⋅ 5 2 ⋅ 33
38. 1)
(
40. (7
38 2 − 17 2
47 2 − 19 2
;
2
3k
k
.
35.
.
36.
.
37.
34n +3 ⋅ 33n− 2
32 n −1
a 7 y −5 ⋅ a 3 y + 2
.
a 5 y −3
2 ⋅ 522 − 9 ⋅ 5 21
2510
.
(4 ⋅ 3 + 7 ⋅ 3 )⋅ 57 .
(19 ⋅ 27 )
22
2)
.
47 2 − 32
27 2 + 2 ⋅ 27 ⋅ 13 + 132
21
4 2
.
)(
)
): (14 ⋅ 3 ).
39. 12 ⋅ 5 2 n +1 − 8 ⋅ 5 2 n + 4 ⋅ 5 2 n −1 : 4 ⋅ 5 2 n − 2 .
2
⋅ 2 2 ⋅ 32 n +1 + 2 5 ⋅ 7 ⋅ 32 n −1
2 n −1
Раздел VIII. Одночлены, многочлены.
Разложение многочленов на множители
Формулы сокращенного умножения:
a 2 − b 2 = (a − b )(a + b ) ;
(a + b)2 = (a + b)(a + b ) = a 2 + 2ab + b 2 ;
(b − a )2 = (a − b)2 = (a − b )(a − b ) = a 2 − 2ab + b 2 ;
(a + b )3 = a 3 + 3a 2b + 3ab 2 + b3 ;
(a − b )3 = a 3 − 3a 2b + 3ab 2 − b3 ;
a 3 + b 3 = (a + b ) (a 2 − ab + b 2 ) ;
a 3 − b 3 = (a − b ) (a 2 + ab + b 2 ).
27
28.
Разложить на множители.1. 2 x 2 y 4 − 2 x 4 y 2 + 6 x 3 y 3 .
16. x 4 + x 3 + x + 1 .
2. 4 a 2b 2 + 36 a 2b 3 + 6ab 4 .
17. x 3 y 3 + 64 .
3. 4b 2 + 8ab − 12a 2 b .
18. (a + b )3 − (a − b )3 − 8 b3 .
4.
( x − y ) + b( y − x ) .
5. a 2 ( x − 2 ) + b 2 (2 − x ) .
(
) − 4 x y (x + y ).
(a + b )− (a + b ) .
19. x 2 + y 2
3
20. 4 a 2 b 2
2
2 2
2
2
2
2
2 3
6. a (b − 3) + (3 − b ) − b (3 − b ) .
21. 20 x 5 y 4 − 5 x 3 y 2 .
7. 3 m (n − m )2 − 9 m 2 (m − n ) .
22. (a + 3b )2 − (3a + b )2 .
8. a (a − b )2 − (b − a )3 .
23. 9 a 4 − 13a 2 b 2 + 4b 4 .
9. xy 2 − by 2 − ax + ab + y 2 − a .
24. 3 x + xy 2 − x 2 y − 3 y .
10. ax 2 − ay − bx 2 + cy + by − cx 2 .
25. x − y − 3 x 2 + 3 y 2 .
11. x 2 + 3 x + 2 .
26. a − 3b + 9b 2 − a 2 .
12. a 4 + 2 a 3 + 1 .
27. a 3 − ab − a 2b + a 2 .
13. 2 a 4 − a 2 − 1 .
28. 3a 2 + 12b 2 + 12 ab − 12 .
14. m 3 − 12 m 2 + 48 m − 64 .
29. ab 2 − b 2 y − ax + xy + b 2 − x .
15. 1 − a 2 − 2 ab − b 2 .
30. 1 − x 2 + 2 xy − y 2 .
Раздел IX. Понятие о функции и графике функции
Зависимость между переменными y и x называют функциональной (или функцией) и обозначают y(x). При этом x называют независимой переменной, а y — зависимой переменной.
Функция может быть задана с помощью формулы, таблицы или
графика.
28
29.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям независимойпеременной, а ординаты — соответствующим значениям функции.
Графиком функции y = kx при любом значении k является прямая, проходящая через начало координат. Если значения x, y положительны и k > 0, то зависимость вида y = kx называют прямой
пропорциональной зависимостью, а k — коэффициентом пропорциональности.
Кроме прямой пропорциональной зависимости существует обратная пропорциональная зависимость y от x. В этом случае при
увеличении значения x в несколько раз значение y уменьшается во
столько же раз. Обратная пропорциональная зависимость выражаk
ется формулой y = , где k > 0, x > 0.
x
Функция вида y = kx + b , где b и k — заданные числа, называется линейной функцией. Графиком линейной функции является
прямая. Линейная функция строится по двум точкам или путем
сдвига графика y = kx на b единиц вдоль оси ординат.
Для исследования линейной функции удобно находить точки
пересечения графика с осями координат.
Построить графики.
1. Построить графики по точкам:
1) y = –3x +1;
7) y = 7;
2) y = 2,5x + 5;
8) x = – 2;
1
9) y = x;
3) y = − x − 2 ;
3
10) y = –1;
4) y = 4x – 0,5;
5) 2y = x + 3;
11) x = 1,7;
6) 3y – 2x = –1;
2. Построение графиков по точкам и путем сдвига по осям:
1
3) y = 3 − 2 x ;
1) y = 3 x − ;
2
2) y = 2 x − 5 ;
4) y = − 4 − x ;
29
30.
21
11) y = − x − ;
3
2
1
12) y = 1 x + 3 ;
2
1
13) y = −2 x − 1 ;
3
14) 2 y = 3 x − 5 ;
15) 3 y = x − 6 ;
5) y = 1 + x ;
6) y = 1 − x ;
7) y = −1 − x ;
8) y = −1 + x ;
9) y = 4 x + 3 ;
10) y = −5 x + 1 .
3. Построение графиков по точкам пересечения графиков с осями координат:
1) y = – 4,5x + 1;
4) y = – 6x +2;
2) y = 0,6x + 0,5;
5) y = 2x + 2.
3) y = – 2,5x – 5;
4. Построить графики:
1) y = ⏐x⏐ – 1;
13) y = −3 + x − 5 ;
2) y = ⏐x⏐;
14) y = 3 x − 2 ;
3) y = 5 – 2⏐x⏐;
15) y = x − 7 ;
4) y + 3 = –⏐x⏐;
16) y = −2 x + 2 − 1 ;
5) y –⏐x⏐ = 0,5;
17) y = 3 − x ;
6) y = x + 1 ;
18) y = 3 x + 2 − 4 ;
7) y = −1 − x ;
19) y = − x − 7 ;
8) y = 1 − 3 x − 1 ;
20) y = x − 1 + 1 ;
9) y = 2 x − 1 ;
21) y = 5 x + 6 ;
10) y = 5 x + 1 − 1 ;
22) y = 2 − x ;
11) y = 3 − x ;
23) y = x − 2 ;
12) y = 4 x − 2 + 1 ;
24) y = 2 x + 1 − 1 ;
30
31.
25) y = 1 + 2 x ;⎧ x
⎪− 2 при x < − 2 ,
⎪
33) y = ⎨1 при − 2 ≤ x < 1 ,
⎪3 x − 2 при x ≥ 1 ;
⎪
⎩
26) y = 3x − 2 − 3 ;
⎧
⎪2 x + 4 при x < −1 ,
⎪
34) y = ⎨2 при − 1 ≤ x < 2 ,
⎪
x
⎪3 − при x ≥ 2 ;
⎩ 2
27) y = 2 − 5 x ;
⎧ x при x < 0 ,
35) y = ⎨
⎩2 x при x ≥ 0 ;
⎧3 + x при x < 0 ,
28) y = ⎨
⎩3 − x при x ≥ 0 ;
⎧ x + 1 при x < 0 ,
36) y = ⎨
⎩1 при x ≥ 0 ;
⎧− 2 x − 1 при x < 0 ,
29) y = ⎨
⎩2 x − 1 при x ≥ 0 ;
⎧− x + 1 при x ≥ 0 ,
37) y = ⎨
⎩1 при x < 0 ;
⎧− 2 x при x < − 3 ,
⎪
30) y = ⎨6 при − 3 ≤ x ≤ 4 ,
⎪2 x − 2 при x ≥ 4 ;
⎩
38) y =
(x − 2 )2 ;
39) y =
x2 + 6x + 9
;
x+3
⎧ x + 1 при x < 0 ,
31) y = ⎨
⎩1 − x при x ≥ 0 ;
⎧ x + 2 при x ≥ 0 ,
32) y = ⎨
⎩2 − x при x < 0 ;
x−2
40) x y = 3 x 2 − x .
5. Построить графики, используя формулы сокращенного умножения:
1) y = (3 x − 1)2 − (2 x + 1)2 − 5 x 2 + 4 x ;
2) y = (7 x + 2 )2 + ( x − 3)2 − 50 x 2 − 18 x − 11 ;
31
32.
3) y = (x − 7 )2 − ( x + 5)2 + 20 x − 19 ;4) y = (2 x + 1)2 + (2 x − 1)2 − 8 x 2 ;
5) y = (3 x + 2 )2 − (3 x − 2 )2 − 21x − 2 ;
6) y = (x + 4 )2 − (x + 3)2 − 5 ;
7) y = (4 x + 1)2 − (3 x + 2 )2 − 7 x 2 ;
8) y = (5 x − 3)2 − (3 x + 1)2 − 16(x − 1)2 ;
9) y = (7 x − 1)2 − (3 x + 1)2 − 40 x 2 + 17 x + 2 ;
10) y = (5 x + 1)2 − 8 x 2 − (2 x − 1)2 − 12 x 2 − ( x + 1)2 − 8 x ;
11) y = (3x + 2)2 − (2 x + 1)2 − (2 x − 1)2 − ( x + 3)2 ;
12)
y = ( x − 1)3 − (x + 2 )3 + (3 x + 2 )2 + 7;
13) y = (3 + x )3 − (2 x − 1)3 + 7 x 3 − (4 x + 3)2 − 5 x 2 − 14 ;
14) y = ( x + 2 )3 − (x − 2 )3 − 12 x 2 − 11 ;
15) y = (2 x − 1)3 + (x + 2)3 + (3 x − 2)2 − 9 x 3 − 3 x 2 − 10 .
6. Найти координаты точки пересечения графиков функций:
1) y = 10x – 8 и y = – 3x +5;
4) y = 0,1x и y = 14;
2) y = 5x + 16 и y = – 6;
5) y = 14x и y = x +26.
3) y = 4x + 9 и y = 6x – 5;
7. Пересекаются ли графики функций:
1
5
3) y = 0,2x – 9 и y = x + 1 ?
1) y = x и y = – 3x + 3,6;
2) y = – 6x + 9 и y = 2x –7;
8. Найти k и b, если график линейной функции проходит через
точки (–1, 2) и (2, 1). Задайте формулой линейную функцию.
9. График линейной функции y = kx + b проходит через точку
A (2, 1), а угловой коэффициент этой прямой равен 0,5. Задайте
данную линейную функцию формулой и постройте ее график.
32
33.
10. Постройте графики и исследуйте, при каких значения xфункция больше нуля (положительна), меньше (отрицательна) и
равна нулю:
1
1) y = –3,5x + 1,5;
5) y = 5x – ;
3
2) y = – 0,5x + 5;
6) y = 4x + 1;
3) y = 2x – 0,5;
7) y = – 2x – 4.
4) y = 5x+1;
Раздел X. Системы уравнений
Решением системы двух уравнений с двумя неизвестными называют такую пару чисел x и y, которые при подстановке в эту систему обращают каждое ее уравнение в верное равенство. Решить систему уравнений — значит найти все ее решения или установить,
что их нет. Существует три способа решения системы уравнений:
подстановки, сложения и графический.
При решении способом подстановки необходимо:
• из одного уравнения системы (все равно из какого) выразить
одно неизвестное через другое, например, y через x;
• полученное выражение подставить в другое уравнение системы и получить одно уравнение с одним неизвестным;
• решив это уравнение, найти x;
• подставив найденное значение x в выражение для y, найти значение y.
При решении системы уравнений способом алгебраического
сложения необходимо:
• уравнять значения при одном из неизвестных, умножая или
деля каждое из уравнений на необходимые коэффициенты;
• складывая или вычитая полученные уравнения, получить одно
уравнение с одним неизвестным;
• найти первое неизвестное;
• подставляя найденное значение в одно из уравнений исходной
системы, найти второе неизвестное.
При решении системы уравнений графическим способом необходимо:
• построить графики каждого из уравнений системы;
33
34.
• найти координаты точки или точек пересечения построенныхпрямых или установить, что прямые не пересекаются;
• если прямые параллельны, то система решений не имеет;
• если прямые совпадают, то система имеет бесконечное множество решений;
• если прямые имеют одну общую точку, то ее координаты являются решением системы уравнений.
При решении графическим методом находится приближенное
значение неизвестных. Чтобы найти точное решение системы
уравнений необходима проверка, которая подтвердит верное равенство ее уравнений.
Решить системы уравнений.
I тип
⎧x − y = 2 ;
1. ⎨
⎩3x − 2 y = 9 .
⎧2 x + 3 y = 12 ;
9. ⎨
⎩3 x + 2 y = 13 .
⎧x − 2 y = 3 ;
2. ⎨
⎩5 x + y = 4 .
10. ⎨
⎧ x + 2 y = 11 ;
3. ⎨
⎩5 x − 3 y = 3 .
⎧2 x − 5 y = − 7 ;
11. ⎨
⎩x − 3y = − 5 .
⎧ y − 3x = − 5 ;
4. ⎨
⎩2 y + 5 x = 23 .
⎧2 x − 3 y = 1 ;
12. ⎨
⎩3x + y = 7 .
⎧x + 5 y = 7 ;
5. ⎨
⎩ x − 3 y = −1 .
⎧x − 2 y = 7 ;
13. ⎨
⎩ x + 2 y = −1 .
⎧2 x − 3 y = − 5 ;
6. ⎨
⎩3x + 2 y = 5,5 .
⎧x + 4 y = 7 ;
14. ⎨
⎩x − 2 y = − 5 .
⎧2 x − 2 y = 5 ;
7. ⎨
⎩3 x − 2 y = 4 .
⎧3 x − 8 y = 22 ;
15. ⎨
⎩7 x + 8 y = 78 .
⎧3 x + 2 y = 10 ;
8. ⎨
⎩5 x + 3 y = 12 .
⎧15 x − 8 y = 2 ;
16. ⎨
⎩5 x + 3 y = 63 .
⎧(x + 5)( y − 2 ) = (x + 2 ) ( y − 1) ;
⎩(x − 4 )( y + 7 ) = (x − 3)( y + 4 ) .
34
35.
⎧4 x − 3 y = 7 ;17. ⎨
⎩5 x + 2 y = 26 .
⎧35 x − 3 y = 5 ;
20. ⎨
⎩49 x − 4 y = 9 .
⎧9 x − 7 y = 1 ;
18. ⎨
⎩4 x + 3 y = 31 .
⎧5 ( x + 2 y ) − 3 = x + 5 ;
21. ⎨
⎩4 ( x − 3 y ) − 50 = − y .
⎧14 x + 5 z = 14,5 ;
19. ⎨
⎩3x + 4 z = 3,4 .
⎧5 ( x − 3 y ) − 26 = 2 x + 1 ;
22. ⎨
⎩3 ( x − 6 y ) + 4 = 9 y + 19 .
II тип
11x
⎧ x + 5y
+
⎪⎪ 2
1. ⎨
⎪ 2x − 3y − y
⎪⎩
7
− 2y
2x − 4 y + 6
=
;
8
5
− 2x 2 (9x + 7 y )
=
.
5
11
⎧x −1 4 − y
+
= 3;
⎪
2
5. ⎨ 5
3− y 5+ x
⎪
−
= 1.
6
⎩ 2
1
⎧1
⎪3 x + 4 y = 0 ;
2. ⎨
2
3
⎪ x − y = 8,8 .
5
⎩3
⎧1 1 7
⎪⎪ x + y = 12 ;
6. ⎨
2 1 1
⎪ − = .
⎪⎩ y x 6
⎧3
⎪ x−
3. ⎨ 4
1
⎪ x−
⎩4
⎧2 x + 3 y = 13 ;
⎪
13 − 2 x
7. ⎨
y=
.
⎪⎩
3
2
y = 3,6 ;
5
1
y = 0.
3
⎧ x − 6 y +1
−
= 1;
⎪
3
4. ⎨ 2
2 − y x −1
⎪
+
= 2.
2
⎩ 4
⎧3 x + 8 y = −1 ;
⎪
2
8. ⎨
x + 2 y = 5.
⎪⎩
3
III тип
⎧⎪ x 2 − y 2 = 5 ;
1. ⎨
⎪⎩ x + y = −1 .
⎧⎪ x 2 − y 2 = 3 ;
2. ⎨
⎪⎩ x − y = 3 .
35
36.
⎧⎪(7 x + y )2 = − x + 3 y ;3. ⎨
⎪⎩7 x + y = − 2 .
⎧⎪4 x 2 − 28 xy + 49 y 2 = 5 x + 2 y ;
13. ⎨
⎪⎩2 x − 7 y = 2 .
⎧⎪ x 2 − y 2 = 5 ;
4. ⎨
⎪⎩ x − y = −1 .
⎧⎪(2 x + 3 y )2 = −3 x + y ;
14. ⎨
⎪⎩2 x = 4 − 3 y .
⎧⎪(2 x + y )2 = 2(2 x − y ) ;
5. ⎨
⎪⎩2 x + y = 2 .
⎧⎪ x 2 − y 2 = 5 ;
15. ⎨
⎪⎩ x + y = −1 .
⎧(3 x − y )(3 x + y ) = 45 ;
6. ⎨
⎩3x + y = 3 .
⎧⎪ x 2 − y 2 = 3 ;
16. ⎨
⎪⎩ x − y = 3 .
⎧⎪(3 x + 5 y )2 = x + 2 y ;
7. ⎨
⎪⎩5 y + 3 x = 3 .
⎧⎪ x 2 − 6 xy + 9 y 2 = x − y ;
17. ⎨
⎪⎩ x − 3 y = −1 .
⎧⎪(x − 7 y )2 = y + 2 x ;
8. ⎨
⎪⎩ x − 7 y = 5 .
⎧⎪ x 2 + 4 xy + 4 y 2 = − x − 6 y ;
18. ⎨
⎪⎩ x + 2 y = 1 .
⎧⎪ x 2 − 2 xy + y 2 = 2 y − 3x ;
9. ⎨
⎪⎩ x − y = −2 .
⎧⎪4 x 2 + 12 xy + 9 y 2 = 3x + 2 y ;
19. ⎨
⎪⎩2 x + 3 y = 1 .
⎧⎪ x − y = 4 ;
10. ⎨ 2
⎪⎩ x − y 2 = 40 .
⎧⎪(x + 5 y )2 = 2 x − y ;
20. ⎨
⎪⎩ x + 5 y = 3 .
⎧⎪9 x 2 − 12 xy + 4 y 2 = 5 x − 2 y ;
⎧⎪ x 2 − 4 xy + 4 y 2 = 5 x − y ;
11. ⎨
21. ⎨
⎪⎩3x − 2 y = −3 .
⎪⎩ x − 2 y = 2 .
⎧⎪ x 2 + y 2 − 2 xy = − x + 6 y ;
12. ⎨
⎪⎩ x − y = 1 .
⎧⎪(x − y )2 = 10 x − 11y ;
22. ⎨
⎪⎩ x − y = 1 .
36
37.
ОтветыРаздел I. Арифметические примеры
1
12. − 3 .
4
23. 5.
2. −
13. 1,7.
24. – 50.
3.
3
14. − 0,75 = − .
4
25. – 0,05.
15. – 0,4.
26. 1,25.
16. 32.
5
27. − .
9
1. − 0,325 = −
4.
5.
6.
13
.
40
9
.
28
5
− .
9
3
= 0,3 .
10
1
.
4
73
.
210
7. 83,244.
18. 3.
8. 37,4.
19. 1.
9.
2
28. − 42 .
3
17
29. 1 .
33
2
30. 2 .
11
7
31. 27 .
9
17. 0,5.
1
.
3
20. 20.
1
21. − 1 .
9
22. 16.
10. 1.
11. –20.
Раздел II. Признаки делимости
3. 2.
5. Составное.
6. 3111…110 ; 7111…115
15 цифр
9. 3; 7.
10. Да, так как (5 + 8) –2 = 11.
15 цифр
37
38.
Раздел IV. Пропорции9. 1,6.
12. 10,25.
16. 3.
10. 2,5.
13. 19.
17. 1.
11. 6,75.
14. 2,5.
18. 5.
Раздел V. Уравнения
Тип I
1
1. 2 .
7
8
2.
.
17
3. 44.
9. Корней нет.
19. 0,6.
10. Любое значение х
является корнем
уравнения.
11. Любое значение х
является корнем
уравнения.
1
20. − 6 = − 6,125 .
8
21. 1,854.
4. – 5.
1
5. .
3
6. 21.
2
7. 1 .
3
12. Корней нет.
22. 9,9.
13. 0.
23. 2,5.
14. 3.
24. 1, 625.
15. 5.
25. 0,05.
8. 0.
18. – 0,2.
26.
1
.
9
Тип II
1
1. 0; 1 .
5
2. 0;
1
.
8
3. 0; 1; −
4.
2
1
; −1 .
2
3
1
2
; − ; 0; – 4.
3
5
38
2
1
5. 1 ; − .
5
4
6. 1; –1.
39.
7.2
1
;− .
3
2
21. 2; – 2.
1
35. − ; − 0,4 .
3
8.
1
1
; −1 .
4
4
22. –1; 0.
36. 1; 0.
1
1
9. 0; − ; − .
5
3
23. 5; 2; – 2.
1
2
37. 1 ; − 2 .
2
3
10.
5 1
;1 .
7 2
1 1
24. 1 ; − .
2 2
1 2
38. − 2 ; 2 .
2 3
11.
1 1
; .
4 3
25.
2
; − 3.
3
39.
1 3
;
.
8 43
12. – 4; 1.
1
26. 1; − 1 .
2
1 3
40. − ;
.
9 23
13. 6; 8.
27. − 2; 5 .
41.
14. 1; 5.
1 1
28. − ; .
3 4
42. 0,5; – 0,4.
15. 2; – 6.
29.
1
;0.
2
43. 0,8; 1,55.
2 1
16. 1 ; 2 .
3 3
30.
1
3
;− .
3 14
44. 0,45; 0,82.
17. 7; 4.
2
31. − 1 ; 1,5 .
3
2
45. 11 ; 0 .
3
18. 0; 8; 12.
1
32. 2 ; − 2 .
3
46.
1
1
19. 1 ; − 1 .
2
2
2 3
33. − ; − .
3 4
47. 2; 3.
20.
1
1
;− .
2
2
34. 2; – 3.
39
5
; − 0,3 .
7
3
;1.
8
40.
Тип III1. 1.
5. 1,1.
2. 2.
6. Уравнение не имеет
3. −
корней.
5
7. − .
12
2
.
3
4. 1.
1
.
3
1
10. 1 .
6
9.
11. 1.
8. 6.
12. 1.
Тип IV
11. −
1. – 3; –17.
1
(6 не подходит по
6
условию).
2. −
1
(5 не удовлетворяет
5
12. −
1
условию x < − 1 ).
2
1
(11 не подходит по
11
условию).
13. −
3. 1; – 3.
4. 4; – 3.
1
(4 не подходит по
4
условию).
5. 5; – 3.
6. 12; – 12.
Тип V
1. у1 = 1;
у2 = 3;
у3 = – 1;
у4 = – 3;
х1 = 2;
х2 = 0;
х3 = – 4;
х4 = – 2.
5. a = 4;
b = 5.
40
41.
8. x1 = – 1;x2 = 1;
x3 = – 2;
x4 = – 4;
y1 = 5;
y2 = 1;
y3 = – 5;
y4 = – 1.
Тип VI
1.
2.
1− a
,
3
5. а ≠ – 1.
а — любое число.
6. a ≠ 0.
24 + a
,
2
7. а ≠ 8.
a — любое число.
8. а ≠ –7.
8
+ 3; a ≠ 0.
a
6
4.
; a ≠ 2.
a−2
3.
9. а ≠ – 1,2.
11. a1 ≠ 0,
4
a2 ≠ .
7
12. a1 ≠ 0 ,
3
a2 ≠ 2 .
5
13. a1 = 0 ,
10. а ≠ 2.
Раздел VI. Задачи
Тип I
1.
2.
3.
4.
5.
6.
8.
9.
2560.
1100 — в первом элеваторе; 2200 — во втором.
В первой — 40; во второй — 36; в третьей — 43;
9.
Первый угол — 70°; второй —35°; третий — 75°.
72 детали.
3,6; 2,1; 1,5.
2,5; 3,3; 8.
Тип II
1. 2,5.
41
a2 = 8 ,
42.
Тип III1. 750 км/ч.
2. 70 км/ч.
3. 45 км/ч.
Тип IV
1. 500; 400 м3.
4. 27 %.
3. 300; 450 руб.
6. 98.
Тип V
1. 20; 3.
6. 540; 350 руб.
4. 18; 12.
7. 900; 500 руб.
Тип VI
1. 12 дней; 24 дня.
2.
ab
.
a+b
3.
ab
.
b−a
Тип VII
1. 1600 м2.
2. Исходное число 96. Обратное число 69.
3. 180 м.
Раздел VII. Степени
9. a 2 .
14. 12.
2. 5 .
10. 1.
15. 2592.
3. 310.
11. c 2 .
16. 80.
7. 1.
12. z 4 .
17. 15.
8. x12 .
13. x 4 .
18. 21.
1. 56.
17
42
43.
619. 3 .
7
b6
20. 4 .
a
27. 30.
35. a5y.
28. 70.
36. 5.
21. 2,8.
29. 0,01.
37.
22. 9.
30. 24.
38. 1)
23.
31. 20.
39. 330.
40. 142.
25. 11250.
26. 270.
32. 20.
33. 9.
34. 35n+2.
8
.
81
24. 8.
1
.
9
3
5
; 2) 1 .
8
8
Раздел VII. Одночлены, многочлены.
Разложение многочлена на множители
(
)
5. (x − 2 )(a − b )(a + b ) .
20. − a 2 + b 2 (a − b )2 (a + b )2 .
9. (x – b +1) (y2 – a).
21. 5 x 2 y 2 (2 xy − 1)(2 xy + 1) .
11. (x + 2) (x + 1).
22. 8(b − a )(a + b ) .
(
)
12. (a + 1) a 3 + a 2 − a + 1 .
(
)(
)
23. 3a 2 − 2b 2 − ab 3a 2 − 2b 2 + ab .
13. (a – 1) (a + 1) (2a + 1).
24. (x − y )(3 − xy ) .
14. (m − 4 )3 .
25. (x − y )(1 − 3x − 3 y ) .
15. (1– a – b) (1 + a + b).
26. (a − 3b )(1 − a − 3b ) .
16. (x + 1) (x + 1) (x2 – x +1).
27. a (a − b )(a + 1) .
17. (xy + 4) (x2y2 – 4xy + 16).
28. 3 (a + 2b − 2)(a + 2b + 2 ) .
18. 6b (a − b )(a + b ) .
29. b 2 − x (a − y + 1) .
19. x 2 + y 2 (x − y )2 ( x + y )2 .
30. (1 − x + y )(1 + x − y ) .
2
(
(
)
43
)
44.
Раздел X. Системы уравненийТип I
1. (5; 3).
9. (3; 2).
17. (4; 3).
2. (1; – 1).
10. (7; 5).
18. (4; 5).
3. (3; 4).
11. (4; 3).
19. (1; 0,1).
4. (3; 4).
12. (2; 1).
20. (1; 10).
5. (2; 1).
13. (3; – 2).
21. (7; – 2).
6. (0,5; 2).
14. (– 1; 2).
22. (14; 1).
7. (– 1; – 3,5).
15. (10; 1).
8. (– 6; 14).
16. (6; 11).
Тип II
2. (6; – 8).
6. (3; 4).
3. (8; 6).
7. Бесконечное множество решений.
4. (– 10; 28).
8. Система не имеет решений.
4
5
5. ⎛⎜ 2 ; − 1 ⎞⎟ .
⎝ 11
11 ⎠
Тип III
1. (– 3; 2).
5. (1; 0).
9. (0; 2).
2. (2; – 1).
6. (3; – 6).
10. (7; 3).
3. ⎜ − ; 1 ⎟ .
⎝ 11 11 ⎠
7. (– 39; 24).
11. (6; 10,5).
4. (– 3; – 2).
8. (12; 1).
12. ⎜1 ; ⎟ .
⎝ 5 5⎠
⎛
5
2⎞
44
⎛ 2
2⎞
45.
2 ⎞⎛ 32
13. ⎜ ; − ⎟ .
⎝ 39 39 ⎠
17. (2; 1).
14. (– 4; 4).
18. ⎜ 2; − ⎟ .
2⎠
⎝
15. (– 3; 2).
19. ⎜ ; ⎟ .
⎝5 5⎠
16. (2; – 1).
20. ⎜ 4 ; − ⎟ .
⎝ 11 11 ⎠
⎛
⎛1
⎛2
2⎞
21. ⎜ ; − ⎟ .
3⎠
⎝3
1⎞
1⎞
⎛ 4
3⎞
45
22. (10; 9).
46.
ГЕОМЕТРИЯСправочник по геометрии
1. Смежные углы.
Теорема. Сумма смежных углов равна 180°:
∠ 1 + ∠ 2 = 180° .
2. Вертикальные углы.
Теорема. Вертикальные углы равны.
∠1 = ∠ 3 ;
∠ 2 = ∠ 4.
3. Равенство треугольников.
Признаки равенства треугольников:
1) a1 = a ; b1 = b ; ∠ C1 = ∠ C ;
2) b1 = b ; ∠ C1 = ∠ C ; ∠ A1 = ∠ A ;
3) a1 = a ; b1 = b ; c1 = c .
B
c
A
B1
а
b
c1
C
A1
46
a1
b1
C1
47.
4. Равенство прямоугольных треугольников.Признаки равенства прямоугольных треугольников:
1) ∠ B1 = ∠ B; a1 = a ;
2) ∠ B1 = ∠B ; c1 = c ;
3) a1 = a ; b1 = b ;
4) a1 = a ; c1 = c ;
∠ C1 = ∠ C = 90 .
5. Равнобедренный треугольник.
Определение. Равнобедренным называется треугольник, у которого две стороны равны.
B
AB = BC .
A
D
C
Теорема. В равнобедренном треугольнике углы при основании
равны:
∠BAC = ∠BCA.
Теорема. В равнобедренном треугольнике медиана, проведенная
к основанию, является биссектрисой и высотой:
BD ⊥ AC ;
AD = DC ;
∠ ABD = ∠ DBC .
6. Сумма углов треугольника:
Теорема. Сумма углов треугольника равна 180°.
B
∠ A + ∠ B + ∠ C = 180° .
A
47
C
48.
7. Внешний угол треугольника.Теорема. Внешний угол треугольника равен сумме внутренних,
не смежных с ним.
∠1 = ∠ 2 + ∠ 3.
8. Прямоугольный треугольник с углом 30°.
Теорема. В прямоугольном треугольнике катет, лежащий против угла в 300, равен половине гипотенузы.
А
BC =
AB
.
2
С
9. Параллельные прямые.
a) ∠ 4 = ∠ 6; ∠ 3 = ∠ 5 — внутренние накрест лежащие углы;
б) ∠ 1 = ∠ 5; ∠ 2 = ∠ 6;
∠4 = ∠8; ∠3 = ∠7 —
соответственные углы;
в) ∠ 4 + ∠ 5 = 180°;
∠3 + ∠6 = 180° — внутренние
односторонние углы.
48
В
49.
10. Вписанная окружность.Теорема. Центр вписанной окружности находится в точке пересечения биссектрис.
11. Описанная окружность.
Теорема. Центр описанной окружности находится в точке пересечения серединных перпендикуляров.
49
50.
ЗадачиРаздел I. Смежные и вертикальные углы
1. Геометрия на готовых чертежах:
а) Дано: α − β = 30° .
Найти: α, β .
β
α
б) Дано: ∠ 1 = ∠ 4 .
Доказать: ∠ 2 = ∠ 3 .
1
2
в) Дано: α : β = 1 : 5 .
Найти: α, β .
3
4
β
α
В
г) Дано: ∠ 1 = ∠ 2 .
Доказать:
∠ BAC + ∠ ACD = 180° .
С
А
1
2
D
50
51.
д) Дано:∠ 1 + ∠ 2 = 180 ° .
Доказать:
1) ∠ ABC = ∠ ACB ;
2) ∠ DBC = ∠ BCE .
D
B
1
2
A
C
е) Дано: ∠ 2 = ∠ 3 .
Доказать:
1) ∠ 1 = ∠ 3 ;
2) ∠ 3 + ∠ 4 = 180° .
E
1
2
4
3
2. Из двух смежных углов один больше другого на 20°. Найти
эти углы.
3. Градусные меры двух смежных углов относятся, как 2:7. Найти эти углы.
4. Сумма двух углов, образованных при пересечении двух прямых, равна 150°. Найти величины углов, образованных прямыми.
5. Из точки проведены шесть полупрямых: OA; OB; OC; OD; OE;
OF, которые образуют углы:
∠ AOB = 38°; ∠ BOC = 50°; ∠ COD = 92°; ∠ COЕ = 130°; ∠ EOF = 12° ;
∠ EOA = 142° . Какие углы являются вертикальными?
Раздел II. Равенство треугольников.
Сумма углов треугольника
В
1. Геометрия на готовых чертежах.
а) Дан треугольник ABC.
Найти неизвестные углы ΔАВС.
70°
51
А
С
52.
Вб) Дан треугольник ABC.
Найти неизвестные углы ΔАВС.
50°
А
С
В
в) Дан треугольник
ABC, BD — медиана.
Найти неизвестные углы
ΔАВС.
30
°
А
С
D
B
D
г) Дано: AB || CD.
Найти неизвестные углы ΔАВС.
60°
°
50
A
C
д) Дан треугольник ABC,
BD — медиана.
В
С
Найти ∠ ABC .
D
А
B
е) Дан рисунок.
Найти ∠ EKC .
P
β
K
A
52
α
γ
E
C
53.
Вж) Дано: прямоугольный треугольник ABC, ∠ C = 90°, ∠ A = 30°,
∠ BEC = 60°, ЕС = 7.
А
Найти АЕ.
60°
30°
Е
С
7
В
з) Дано: треугольник ABC, АВ = ВС;
АО = ОС.
Доказать: AD = CE.
Е
О
А
D
C
2. Один из углов треугольника равен 110°. Чему равны углы,
образованные пересечением биссектрис, проведённых из двух других углов?
3. В треугольнике два угла относятся как 5:8, а третий угол
больше самого меньшего угла на 18°. Найти углы треугольника.
4. В равностороннем треугольнике АВС на трёх сторонах взяты
точки K, L, M так, что AK = BL = CM. Найти углы треугольника
KLM.
5. Докажите равенство треугольников, если равны их основания
и проведенные к ним высоты и медианы.
6. Докажите равенство треугольников по двум углам и высоте,
проведенной из вершины третьего угла.
Раздел III. Равнобедренные треугольники
1. Геометрия на готовых чертежах.
Доказать, что ΔАВС — равнобедренный.
53
54.
а)г)
B
B
D
А
A
C
E
D
C
б)
д)
D
E
B
A
E
C
D
A
в)
B
D
A
E
C
54
B
F
C
55.
2. Медиана, проведённая к одной из боковых сторон равнобедренного треугольника, делит его периметр на две части длиной 15и 6 см. Определить стороны треугольника.
3. В треугольнике АВС известны стороны: АВ = 10 см, а АС =
= 14 см. На стороне АВ взята точка М так, что АМ : МВ = 2:3, а на
стороне АС — точка К, причем АК : КС = 2:5. В каком отношении
биссектриса угла А делит отрезок МК?
4. В треугольнике АВС сторона АВ = 12, а ВС = 9; CN — медиана. Точка М делит отрезок ВС в отношении ВМ : МС = 2:1. В каком
отношении биссектриса ВD делит отрезок NM.
5. В треугольнике АВС прямая CD делит угол АСВ в отношении
1:2. Отрезки AD = DC = CB. Найти углы треугольника.
6. В треугольнике АВС известно, что АВ = 5; ВС = 6; СА = 7. На
сторонах АВ, ВС и СА взяты точки К, L и М так, что прямые KL,
LM, MK перпендикулярны биссектрисам углов В, С, А соответственно. На какие отрезки делят точки K, L и М стороны треугольника АВС?
7. В равнобедренном треугольнике ABC основание AC = 48 см,
внешний угол при вершине B = 600. Найти расстояние от вершины
C до прямой, содержащей AB.
8. Биссектриса равнобедренного треугольника, проведенная из
вершины при основании, образует с противолежащей стороной
углы, один из которых равен 60°. Найти углы этого треугольника.
(Рассмотреть все варианты.)
Раздел IV. Признаки и свойства параллельных прямых
1. Геометрия на готовых чертежах.
а) Дано:
∠ ABE = ∠ CBE .
В
С
Найти: ∠ x .
х
129°
52°
А
Е
55
D
51°
56.
б) Дано: ∠ MPT = ∠ TPK .N
T
112°
Найти: ∠ x .
х
K
68°
68°
M
P
a
в) Дано: a || b.
Доказать: ∠ MOE = 90°.
b
г) Дано:
Доказать: AB || CD.
д) Дано: AB = BC.
Доказать: a || b.
56
57.
2. Параллельные прямые AB и CD пересечены прямой BD. Биссектрисы углов ABD и BDC пересекаются в точке K. ОтрезокBD = 2 KD. Найти углы, образованные секущей BD c прямыми AB и
CD.
Раздел V. Окружность
1. Геометрия на готовых чертежах.
а) Дан рисунок.
B
C
Доказать: CD = BA.
E
F
O
A
D
C
б) Дано: AB = CD.
A
Доказать: OK = OP.
P
O
K
D
B
A
в) Дано: АС — касательная.
B
C
Доказать: OA = OC.
O
57
58.
г) Дано:AB и AC — касательные.
B
A
.O
Доказать: АВ = АС.
C
2. Даны две равные касающиеся окружности. Под каким углом
пересекаются прямые, одна из которых касается этих окружностей
в разных точках, а вторая проходит через центр одной из окружностей и касается другой?
3. В треугольник АВС вписана окружность. Касательные, проведённые к окружности отсекают от исходного треугольника три
треугольника, содержащие вершины А, В и С соответственно. Найти периметры отсечённых треугольников, если стороны треугольника равны 9, 8, 7.
Раздел VI. Задачи на построение
1. Деление отрезка пополам.
2. Построение перпендикуляра к прямой из точки на прямой и
из точки вне прямой.
3. Построение угла, равного данному.
4. Деление угла пополам.
5. Построение треугольника по трём заданным сторонам.
6. Построение прямой параллельной данной и проходящей через
заданную точку.
7. Дан угол 19°. Как построить угол, равный 1°.
8. Дан угол 19°. Как построить луч, который делит этот угол на
части 9 и 10°.
58
59.
Раздел VII. Задачи на повторениеВ этот раздел включены геометрические задачи, для решения
которых надо применять различные теоремы, пройденные в 7-м
классе. Эти задачи наиболее трудные и могут рассматриваться в
конце учебного процесса и как дополнительные задачи. (Часть текстов приведённых задач взята из задачника И.Ф. Шарыгин,
Р.К. Гордин «Сборник задач из геометрии 5000 задач с ответами»).
1. В равнобедренном треугольнике АВС с основанием АС проведена медиана ВM. На ней взята точка D. Докажите равенство
треугольников: а) АВD и CBD; б) AMD и CMD.
2. Отрезки АВ и СD пересекаются под прямым углов и АС =
= АD. Докажите, что ВС = ВD и ∠ АСВ = ∠АDВ.
3. В треугольнике АВС проведены биссектрисы из вершин А и В.
Точка их пересечения обозначена через D. Найти угол АDВ, если:
а) ∠А = 50º, ∠В = 100º; б) ∠А = α, ∠В = β; в) ∠С = 130º г) ∠С = γ.
4. Дан равнобедренный треугольник АВС с основанием АС;
СD — биссектриса угла С; ∠АDС = 150º. Найти угол В.
5. В треугольнике известны величины углов А, В, С. Найдите
углы шести треугольников, на которые данный треугольник разбивается его биссектрисами.
6. Прямая, проходящая через вершину А треугльника АВС, пересекает сторону ВС в точке М. При этом ВМ = АВ; ∠ВАМ = 35º;
∠САМ = 15º. Найти углы треугольника АВС.
7. Высоты треугольника АВС, приведённые из вершин А и С,
пересекаются в точке М. Найдите ∠АМС, если ∠А = 70º, ∠С = 80º.
8. В равнобедренном треугольнике АВС высоты АD и СЕ, опущенные на боковые стороны, образуют угол АМС, равный 48º.
Найдите углы треугольника АВС.
9. Угол при основании ВС равнобедренного треугольника АВС
вдвое больше угла при вершине, ВD — биссектриса треугольника.
Докажите, что АD = ВС.
10. В треугольнике АВС на стороне АС отмечена точка К так,
что АК = АВ. Угол АВК = 75º. Угол АВС = 60º. Найти АС, если известно, что ВС = 3.
59
60.
11. В прямоугольном треугольнике АВС ∠А= 90º, ∠В = 75º. Настороне АС взята точка D так, что ∠АDВ = 2∠DВС. Найти длину
отрезка DС, если АВ = 5.
12. В треугольнике АВС угол А = α, угол С = β. Найдите угол
между высотой и биссектрисой, проведёнными из вершины В:
а) α = 50º, β = 20º; б) α = 110º, β = 50º.
13. Параллельные прямые а и b пересечены секущей АВ (А ∈ а;
В ∈ b ). Биссетрисы внутренних односторонних углов пересекаются в точке С. Через точку С проведена прямая параллельная а, которая пересекает АВ в точке Е. Найти длину отрезка СЕ, если
АВ = 12 см.
60
61.
ОтветыРаздел I. Смежные и вертикальные углы
2. 80° и 100°.
4. 75° и 105°.
3. 40° и 140°.
5. ∠ BOA и ∠ DOE ;
∠ AOE и ∠ BOD .
Раздел II. Равенство треугольников
Сумма углов треугольника
2. 145° и 35°.
3. 45°, 63° и 72°.
4. 60°.
Раздел III. Равнобедренные треугольники
2. 10; 10; 1.
3. 1:1.
4. 1:1.
5. 30°; 60°; 90° и 40°; 60°; 80°.
6.
B
L
K
A
C
M
Δ LMC — равнобедренный (высота совпадает с биссектрисой);
LC = MC = X ⇒ AM = 7 − X ; BL = 6 − X ;
Δ BLK — равнобедренный;
BL = BK = 6 − X ⇒ AK = 5 − (6 − X ) = X − 1 ;
61
62.
Δ АKМ — равнобедренный;АК = АМ ⇒ Х − 1 = 7 − Х ⇒ Х = 4 .
Ответ: СL = СМ = 4 ; ВL = ВК = 2 ; АМ = АК = 3 .
AB = 5; BC = 6; AC = 7.
7. 24 см.
8. 1) 40°; 40°; 100°;
2) 80°; 80°; 20°.
Раздел IV. Признаки и свойства параллельных прямых
2. 60°; 120°.
Раздел V. Окружность
2.
A
B
K
D
o1
F
o2
E
AO1 = DO1 = BO2 = EO1 = R;
O1O2 = 2R.
1
Из ΔO1O2D (∠ D = 90°; O1D = O1O2 ) находим ∠ DO2O1 = 30° .
2
1
Из ΔO1O2E ( ∠ E = 90° ; O1E = O1O2 ) находим ∠ EO2O1 = 30° .
2
62
63.
O1O2 || AB; ∠ O1O2 K = ∠ O2 KB = 30° (внутренние накрест лежащие).∠ O1O2 E = ∠ BFO2 = 30° (соответственные).
Ответ: 30° .
3.
B
М
S
N
T
Q
L
K
G
P
A
D
E
F
C
AQ = AE = x (см. 1, г);
BQ = BT = y;
CT = CE = z;
⎧x + y = 7 ;
⎪
+⎨x + z = 8 ;
⎪y + z = 9 .
⎩
2x + 2y + 2z = 24;
x + y + z = 12;
x = 3; y = 4; z = 5.
KQ = KP;
DP = DE.
Периметр ΔAKD = AK + (KP + PD) + AD = AK + (KQ + DE) +AD =
= 2AQ = 6.
Периметр ΔBNM = 2BQ = 8 (аналогично).
Периметр ΔCLF = 2CF = 10 (аналогично).
Ответ: 6; 8; 10.
63
64.
Раздел VII. Задачи на повторение1.
Дано: ΔABC, AB = BC, AM =
= MC; D ∈ BM.
Доказать: а) ΔABD = ΔCBD;
б) ΔAMD = ΔCMD.
Доказательство.
1. BM — медиана по услоD
вию), так как ΔABC — равнобедренный, то BM — биссектриса и высота.
M
∠ABM = ∠CBM,
∠BMA = ∠BMC = 90º.
A
C
2. Рассмотрим ΔABD и ΔCBD:
M
AB = BC (по условию); BD —
общая; ∠ABD = ∠CBD (по п.1). Следовательно, ΔABD = ΔCBD (по
двум сторонам и углу между ними).
3. Рассмотрим ΔADM и ΔCDM; AM = MC (по условию), DM —
общая; ∠AMD = ∠CMD = 90º (по п.1). Следовательно, ΔAMD =
= ΔCDM (прямоугольный по двум катетам).
Что и требовалось доказать.
B
2.
C
A
O
B
D
64
Дано:
AB ∩ CD = O,
AC = AD; AB ⊥ CD.
Доказать:
а) BC = BD;
б) ∠ACB = ∠ADB.
Доказательство.
1. ΔACD — равнобедренный (AC = AD по условию), AO — высота,
следовательно,
AO —
биссектриса и медиана.
CO = OD
и
∠CAO =
= ∠DAO.
65.
2. Рассмотрим ΔACB и ΔADB. AC = AD (по условию), AB — общая, ∠CAB = ∠DAB (по п.1). Следовательно, ΔACB = ΔADB (подвум сторонам и углу между ними).
3. Из равенства ΔACB = ΔADB следует, что BC = BD и
∠ACB = ∠ADB.
Что и требовалось доказать.
3.
A
M
D
B
K
C
Дано: ΔABC, ∠BAK =
= ∠KAC;
∠ABM =
= ∠MBC ;
а) ∠A = 50º, ∠B = 100º;
б) ∠A = α, ∠B = β;
в) ∠C = 130º;
г) ∠C = γ.
Найти: ∠ADB.
Решение.
1. Рассмотрим ΔABD. ∠ABD = 50º, ∠BAD = 25º, следовательно,
∠ADB = 180º – 50º – 25º = 105º.
β
α
, ∠BAD = , следовательно,
2. ∠A = α, ∠B = β. ∠ABD =
2
2
β α
α+β
∠ADB = 180º – – = 180º –
.
2 2
2
3. ∠C =130º. ∠BAD = xº, ∠ABD = yº, следовательно, ∠A = 2xº,
∠B = 2yº;
2x + 2y + 130º = 180º;
2x + 2y = 50º;
x + y = 25º;
x + y + ∠ADB = 180º;
∠ADB = 180º – (x + y) = 180º – 25º = 155º.
65
66.
4. ∠C = γ. ∠BAD = x, ∠ABD = y, следовательно, ∠A = 2xº,∠B = 2yº.
2x + 2y + γ = 180º;
2x + 2y = 180º – γ;
γ
x + y = 90º – ;
2
γ
γ
∠ADB = 180º – (x + y) = 180º – 90º + = 90º + .
2
2
α+β
Ответ: а) ∠ADB = 105º; б) ∠ADB = 180º –
; в) ∠ADB =
2
γ
= 155º; г) ∠ADB = 90º + .
2
4.
B
Дано: ΔABC — равнобедренный; АВ = ВС;
∠АСD = ∠DCВ;
∠СDA = 150º.
Найти: ∠B.
D
A
C
Решение:
∠ACD = ∠DСВ = хº;
∠С = 2х, ∠А = 2х;
х + 2х + 150º = 180º (из ΔACD).
3х = 30º, x = 10º;
∠А = ∠С = 20º;
∠В = 180º – 40º = 140º.
Ответ: ∠В = 140º.
66
67.
5.B
C1
А1
O
А
В1
C
Дано: ΔABC, АА1;
ВВ1; СС1 — биссектрисы ∠A; ∠В; ∠С;
АА1 ∩ ВВ1 = О.
∠AOB1,
Найти:
∠OB1A,
∠OAB1,
∠COB1,
∠OB1C,
∠OCB1,
∠COA1,
∠OA1C, ∠OCA1.
Решение.
∠A
∠B
(по условию); ∠ABB1 =
(по условию).
2
2
2. Рассмотрим ΔABB1:
∠B
∠BB1A = 180º –∠A –
= ∠OB1A (по теореме о сумме углов тре2
угольника);
∠A + ∠B + ∠C = 180º;
∠B
.
∠OB1A = ∠C +
2
3. Рассмотрим ΔAOB1:
∠A
∠AOB1 = 180º –
– ∠OB1A;
2
∠A
∠B ∠A ∠B
.
∠AOB1 = 180º –
– 180º + ∠A +
=
+
2
2
2
2
4. Аналогично углы в остальных треугольниках:
∠C
;
∠OСB =
2
∠B
∠B
;
∠OB1С = 180º – ∠С –
= ∠A +
2
2
1. ∠OAB1 =
67
68.
∠A ∠B;
+
2
2
∠A ∠C
;
∠СOA1 =
+
2
2
∠СOB1 =
∠OA1С = 180º – ∠С –
∠OСA1 =
∠C
и т.д.
2
∠A
∠A
;
= ∠B +
2
2
Ответ: ∠OB1A =∠C +
∠B
∠A ∠B
, ∠AOB1 =
+
и т.д.
2
2
2
6.
B
Дано: ΔABC,
AM ∩ BC = M; АВ = ВM;
∠BAM = 35º; ∠СAM =
= 15º.
Найти: ∠A, ∠B, ∠C.
M
C
A
Решение.
1. ∠A = ∠ВAM + ∠CAM = 35º + 15º = 50º.
2. ΔABM — равнобедренный;
∠BMA = ∠MАC + ∠MCA (теорема о внешнем угле треугольника);
∠MCA = 35º – 15º = 20º.
3. ∠B =180º – ∠A – ∠С (теорема о сумме углов треугольника);
∠В = 180º – 50º – 20º = 110º.
Ответ: ∠A = 50º, ∠В = 110º, ∠C = 20º.
68
69.
7.B
Дано: ΔABC,
AK ⊥ BC;
CN ⊥ AB,
AK ∩ CN = M;
∠A =
= 70º; ∠С = 80º.
Найти: ∠AMC.
K
N
M
C
A
Решение.
1. Рассмотрим ΔANC: ∠A = 70º; ∠N = 90º;
∠АCN = 180º – 70º – 90º = 20º (теорема о сумме углов треугольника).
2. Рассмотрим ΔAKC: ∠C = 80º; ∠K = 90º;
∠CAK = 180º – 80º – 90º = 10º.
3. Рассмотрим ΔAMC: ∠AMC = 180º– ∠MAC – ∠MCA;
∠AMC = 180º – 20º – 10º = 150º.
Ответ: ∠AMC = 150º.
8.
B
E
A
Дано: ΔABC, AB =
= BC, AD, CE — высоты;
AD ∩ CE = M;
∠AMC = 48º.
Найти: ∠A, ∠B, ∠C.
D
M
C
69
70.
Решение.1. ∠A = ∠C = α (углы при основнии равнобедренного треугольника).
2. Рассмотрим ΔAEC: ∠ECA = 180º – 90º – α;
∠ECA = ∠MCA = 90º – α.
3. Рассмотрим ΔADC: ∠DAC = 180º – 90º – α;
∠DAC = ∠MAC = 90º – α.
4. Рассмотрим ΔAMC:
∠AMC + ∠MCA + ∠MAC = 180º (теорема о сумме углов треугольника);
90º – α + 90º – α + 48º = 180º;
2α = 48º; α = 24º.
5. Рассмотрим ΔABC:
∠B = 180º – 2α = 180º – 48º = 132º.
Ответ: ∠A = ∠C = 24º; ∠B = 132º.
9.
A
Дано: ΔABC, AB =
= AC; ∠B = ∠C = 2∠A;
BD — биссектриса.
Доказать: AD = BC.
D
B
C
Решение.
1. ∠A = α; ∠B = ∠C = 2α (по условию);
∠A + ∠B + ∠C = 180º;
α + 2α + 2α = 180º; 5α = 180º; α = 36º;
∠A = 36º; ∠B = ∠C = 72º.
2. ∠ABD = ∠DBC = 36º.
70
71.
3. Рассмотрим ΔABD: ∠A = ∠ABD = 36º, следовательно ΔABDравнобедренный AD = BD.
4. Рассмотрим ΔBDC: ∠DBC = 36º; ∠BCD = 72º (п.1) ∠BDC =
= 180º – 36º – 72º = 72º следовательно ΔBDC равнобедренный BD =
= BC.
5. BD = BC (п.4); AD = BD (п.3) следовательно AD = BС.
Что и требовалось доказать.
10.
Дано: ΔABC; K ∈
∈ AC;
AB = AK;
∠ABK = 75º, ∠ACB =
= 60º; BC = 3.
Найти: AC.
B
A
C
K
Решение.
1. ΔABK — равнобедренный, так как AB = AK (по условию).
Следовательно, ∠ABK = ∠BKA = 75º; ∠BAK = 180º –75º – 75º = 30º
(теорема о сумме углов треугольника).
2. Рассмотрим ΔABC:
∠B = 180º – ∠A – ∠C = 180º – 60º – 30º = 90º. Cледовательно,
ΔABC — прямоугольный с острым углом 30º.
1
Отсюда BC = AC (теорема о катете, лежащем против угла
2
в 30º).
AC = 2BC;
AC = 2 ⋅ 3 = 6 .
Ответ: AC = 6.
71
72.
11.A
Дано: ΔABC, ∠A =
= 90º; ∠B = 75º, ∠ADB =
= 2∠DBC; AB = 5, D ∈
∈ AC.
Найти: DC.
D
B
C
Решение.
1. ∠ADB = 2∠DBC. Пусть ∠DBC = α, тогда ∠ADB = 2α.
2. ∠ADB — внешний угол ΔBDC.
∠ADB = ∠DBC + ∠DCB (теорема о внешнем угле треугольника);
∠DCB = 2α – α = α.
Отсюда, ∠DCB =∠DBC.
Следовательно, ΔBDC — равнобедренный, т.е. BD = DC.
3. Рассмотрим ΔABC:
∠A = 90º, ∠B = 75º;
∠C = 180º – 90º – 75º = 15º (теорема о сумме углов треугольника).
Значит, α = 15º.
4. Рассмотрим ΔABD:
∠BDA = 2α = 30º, ∠A = 90º.
1
Отсюда AB = BD (теорема о катете, лежащем против угла
2
в 30º).
BD = 2AB;
BD = 2 ⋅ 5 = 10 .
5. DC = BD (по п.2).
Значит, DC = 10.
Ответ: DC = 10.
72
73.
12.B
A
H
a) Дано: ΔABC; ∠A =
= 50º, ∠C = 20º; BH ⊥ C;
∠ABD = ∠DBC.
Найти: ∠HBD.
D
C
Решение.
1. ∠B = 180º – 50º – 20º = 110º (теорема о сумме углов треугольника).
110°
= 55° .
2. ∠ABD =
2
3. ΔABD — прямоугольный, ∠ABH = 180º – 90º – 50º = 40º.
4. ∠HBD = ∠ABD – ∠ABH = 55º – 40º = 15º.
Ответ: ∠HBD = 15º.
B
б) Дано: ΔABC; ∠A =
= 110º, ∠C = 50º; BH ⊥
⊥ AC; ∠ABD = ∠DBC.
Найти: ∠HBD.
H
A
D
C
73
74.
Решение.1. ∠АBС = 180º – 110º – 50º = 20º (теорема о сумме углов треугольника).
20°
= 10° .
2. ∠ABD =
2
3. ∠ВAH = 180º – 110º = 70º (смежный).
4. ∠HBА = 180º – 90º – 70º = 20º.
5. ∠HBD = ∠HBA + ∠ABD = 20º + 10º = 30º.
Ответ: ∠HBD = 30º.
13.
K
A
α
E
β
β
B
a
α
α
β
C
c
Дано: a||b; AC,
BC — биссектриса;
СЕ || a; AB ∩ CE =
= E; AB = 12.
Найти: CE.
M
b
Решение.
1. ∠BАС = α; ∠АBС = β; ∠KАС = α; ∠MBС = β.
2. 2α + 2β = 180º (сумма внутренних односторонних углов при
пересечении параллельных прямых секущей); α + β = 90º.
3. ∠АСЕ = α (накрест лежащий с ∠KАС); ∠ВСЕ = β (накрест
лежащий с ∠MBС).
4. ΔAEC — равнобедренный АЕ = ЕС; ΔВEC — равнобедренный ВЕ = ЕС.
1
5. СЕ = АВ; СЕ = 6.
2
Ответ: СЕ = 6.
74
75.
Татьяна Анатольевна ПыжоваГеннадий Викторович Лупенко
Ирина Александровна Масленникова
МАТЕМАТИКА
Учебное пособие
для углубленного изучения математики в 7-м классе
Редактор М.В. Макарова
Оригинал-макет изготовлен Л.М. Бурлаковой
Подписано в печать 09.12.2008. Формат 60х84 1/16
Уч.-изд.л. 4,75 Печ.л. 4,75 Тираж 2000 экз.
Изд. № 052-1 Заказ № 1
Национальный исследовательский ядерный университет «МИФИ».
Типография МИФИ.
115409, Москва, Каширское ш.,31













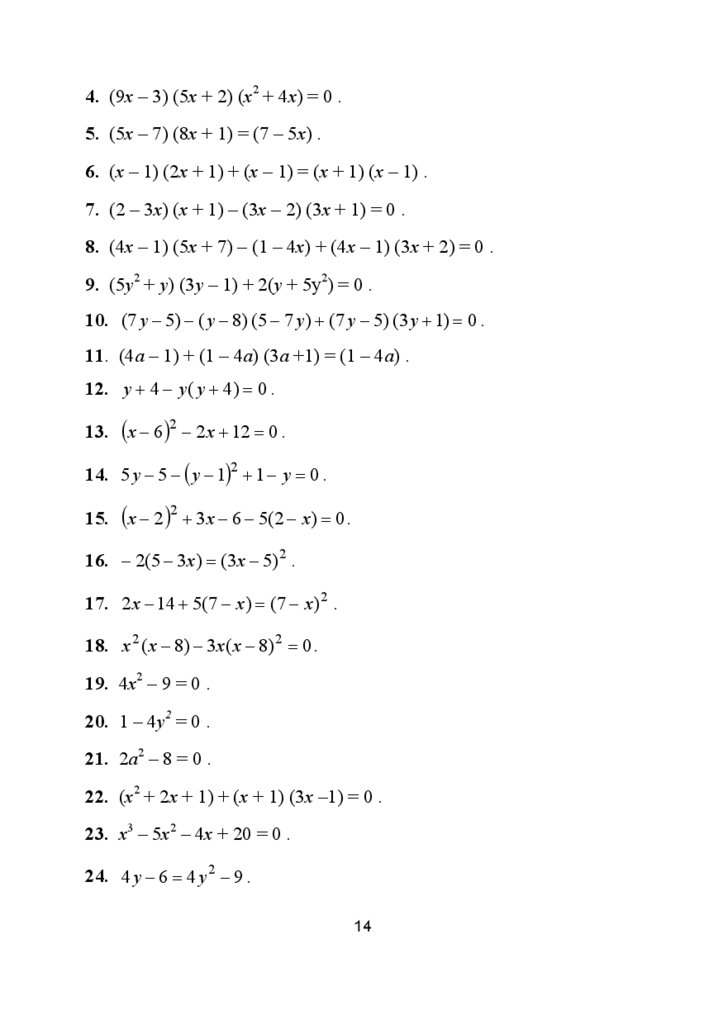


































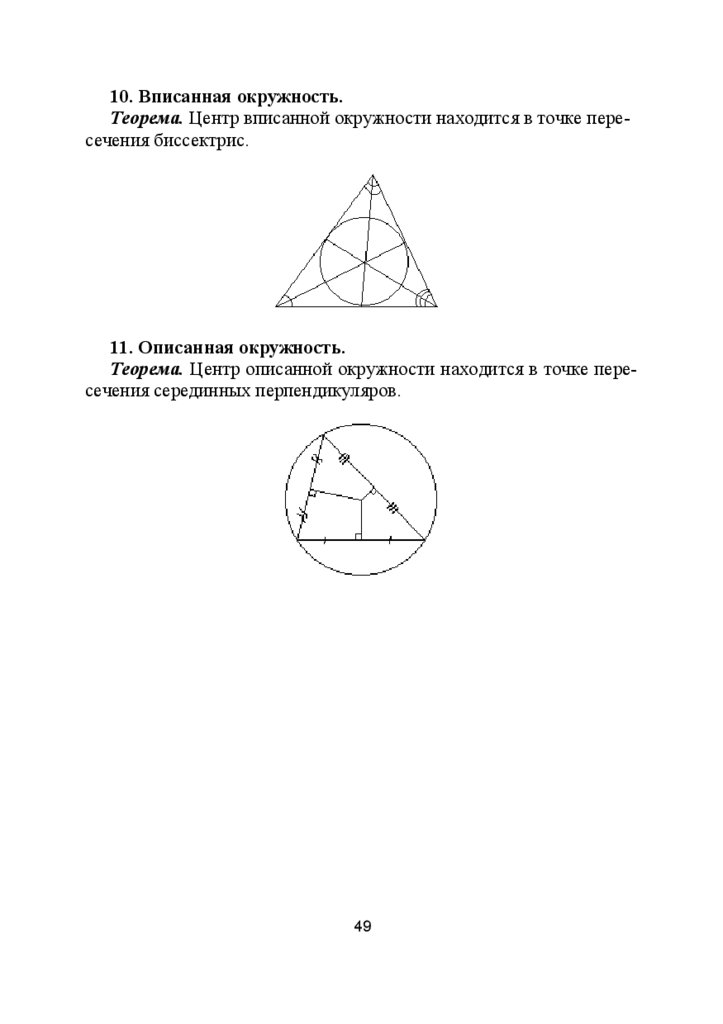
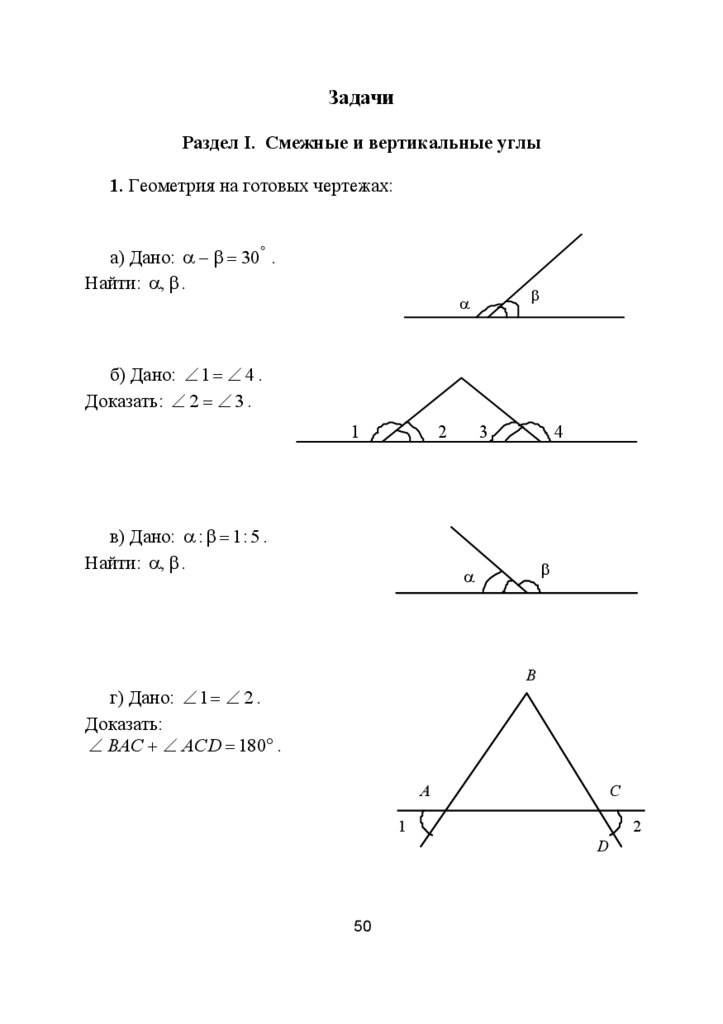

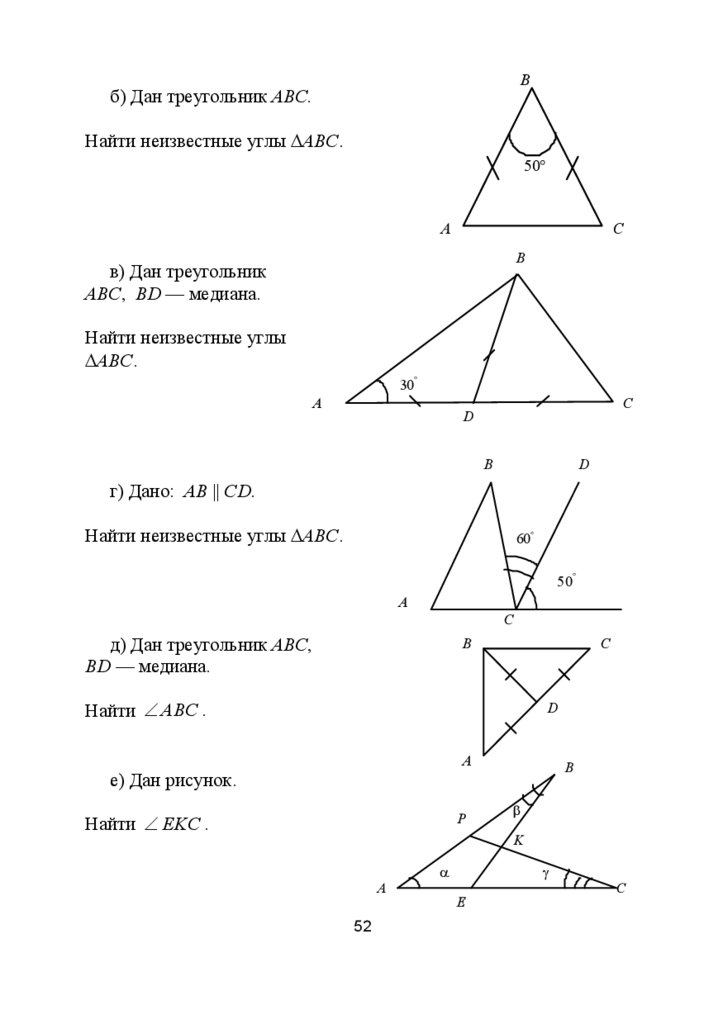

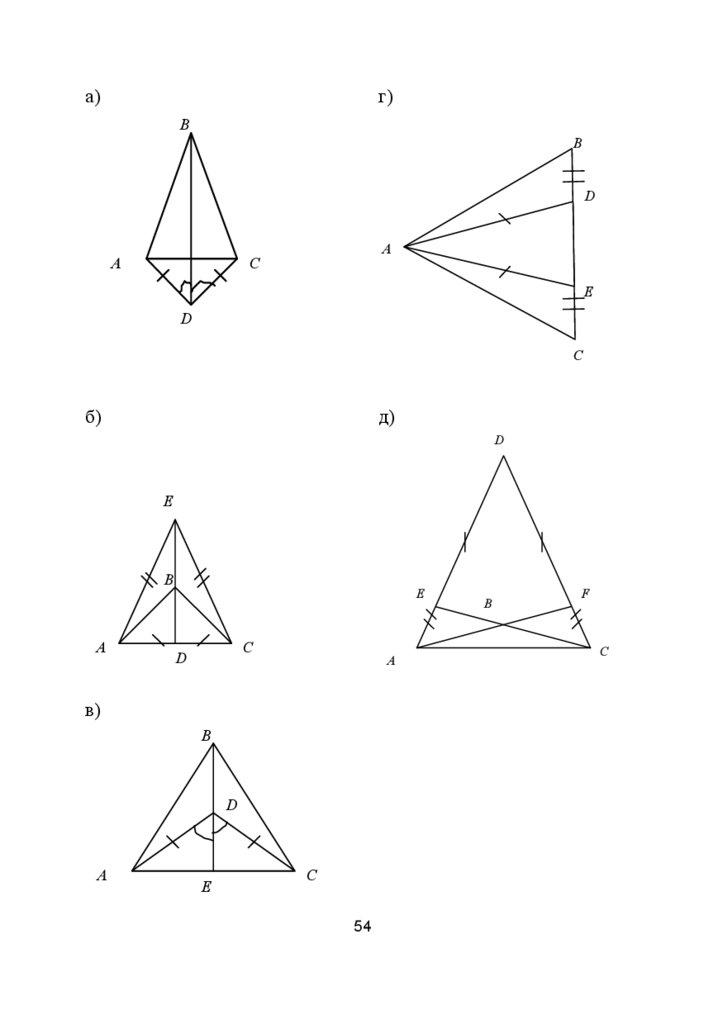

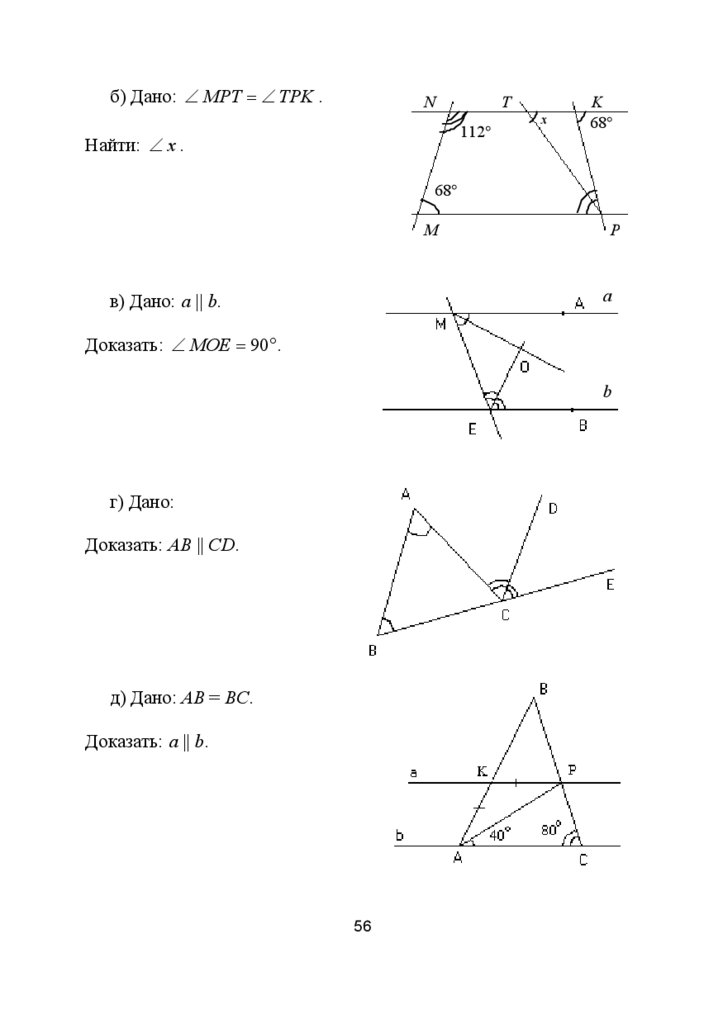
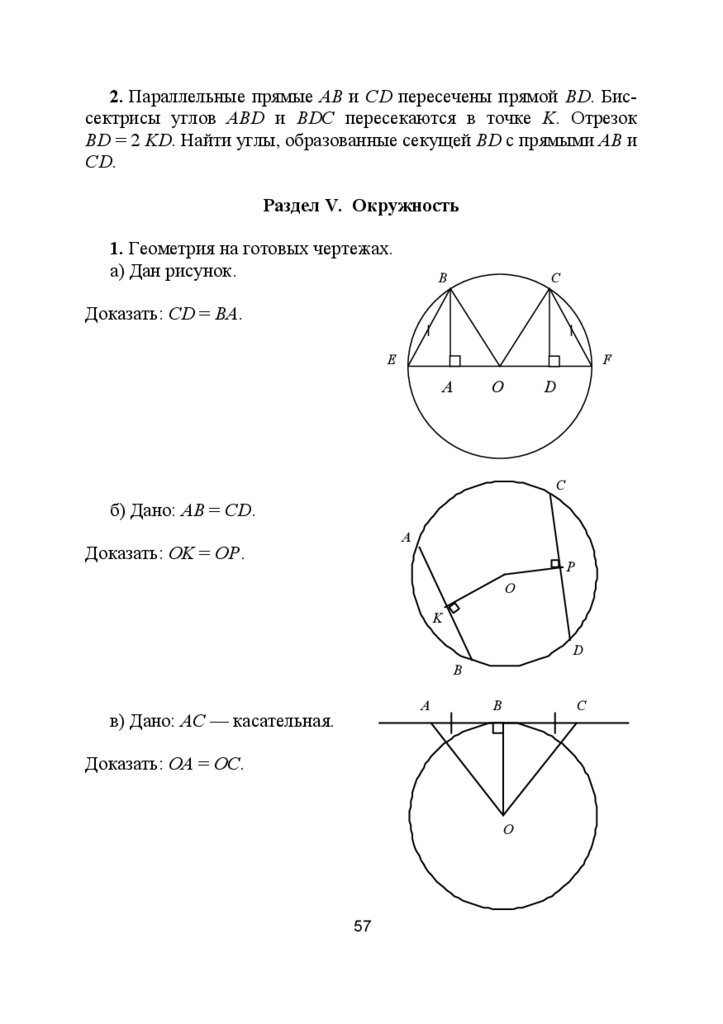





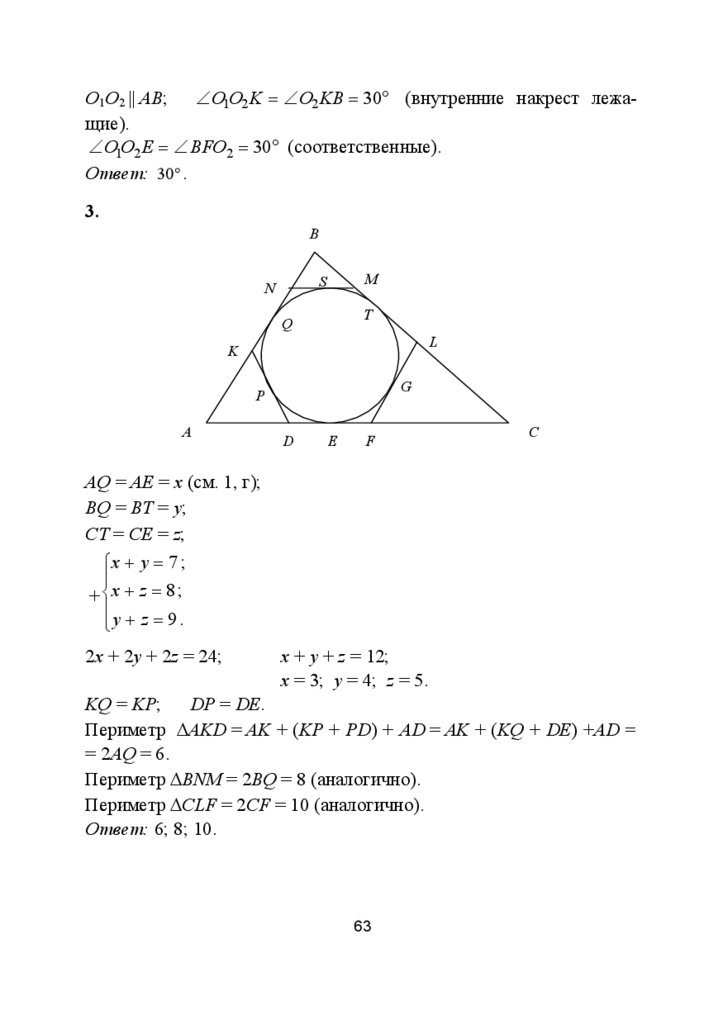
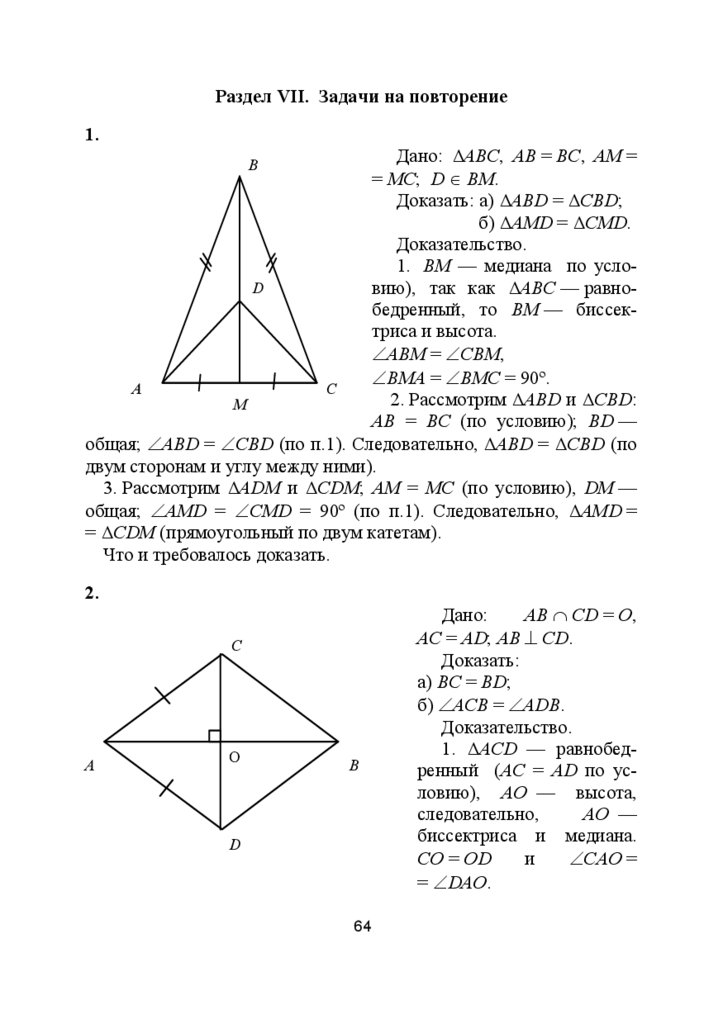


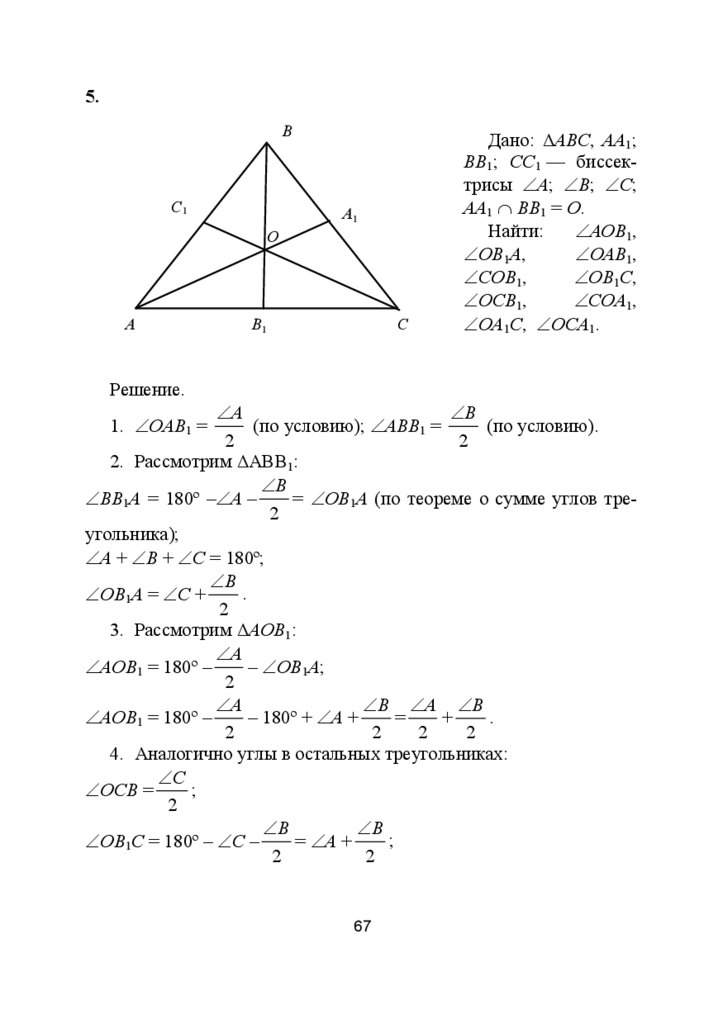

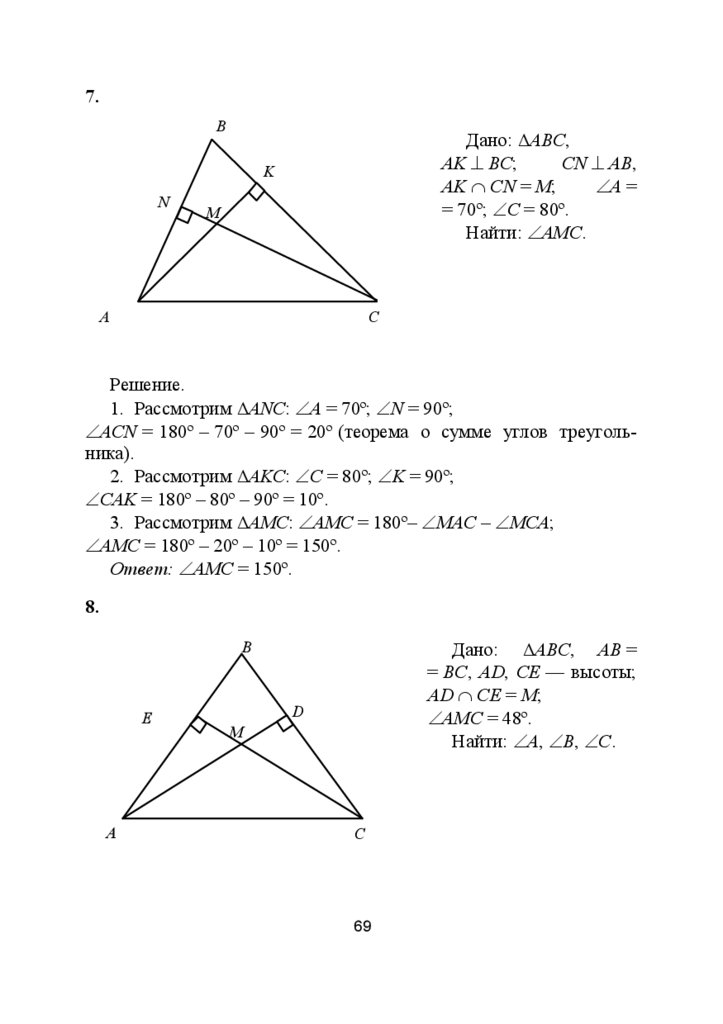



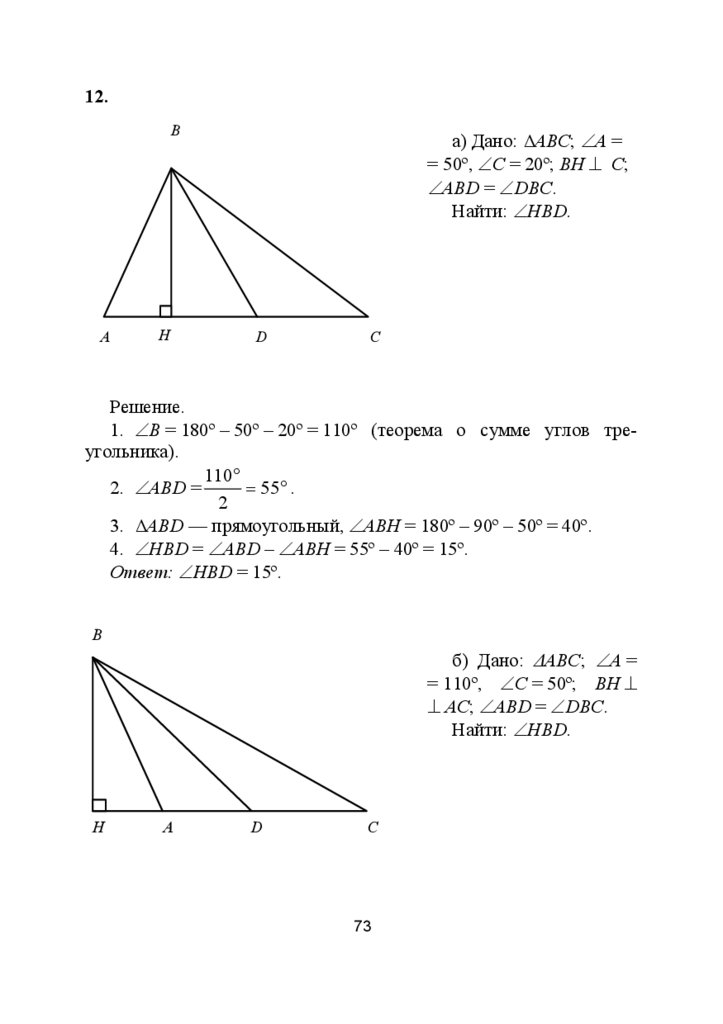
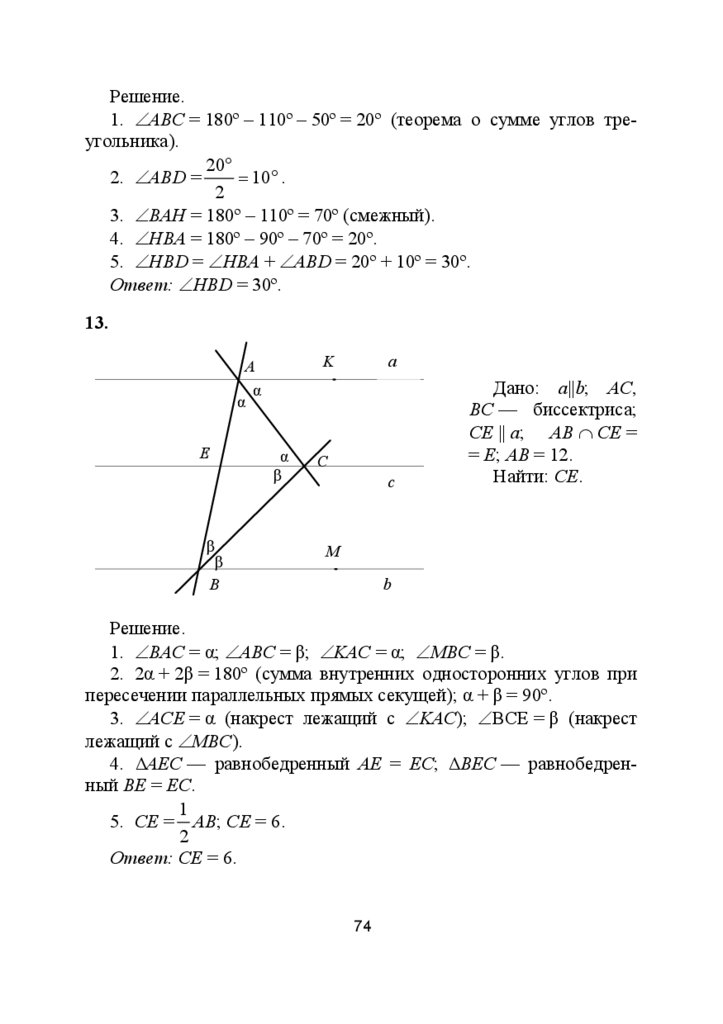


 mathematics
mathematics








