Similar presentations:
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
1.
Күні08.09.2020 ж.
Мамандық
1108000 «Темір жолдың
жылжымалы құрамын пайдалану, жөндеу және
техникалық қызмет көрсету (түрлері бойынша)»
Топ
ТЖДк-1820
Пән
Математика
Тақырып
Теңсіздіктер
2.
3.
ах>b, ax<b, ax≥b, ax≤bбір айнымалысы бар сызықтықтық
теңсіздіктер.
Мұндағы a,b – кез келген бір сандар.
х – айнымалы (белгісіз).
4.
5.
4(х-3)+5х≥3х4х-12+5х≥3х
4х+5х-3х≥12
6х≥12
х≥2
Жауабы: [2;+∞) немесе 2 ≥х
6.
Анықтама: ах²+bх+с>0 , ах²+bх+с<0,ах²+bх+с≥0 , ах²+bх+с≥0 түріндегі
теңсіздіктер квадрат теңсіздіктер деп
аталады.
Мұндағы а≠0.
7. Теңсіздіктің шешімдер жиыны.
D =в2 -4асТеңсіздік
D>0
D<0
D=0
(-∞ ; + ∞ )
(-∞ ; +∞ ) (-∞ ; х1 ) U (х2 ; + ∞ )
1
ах2 + вх +с > 0
2
ах2 + вх +с < 0
3
- ах2 + вх +с > 0
Бос жиын
Бос жиын (х1 ; х2)
4
- ах2 + вх +с < 0
(-∞ ; + ∞ )
(-∞ ; +∞ ) (-∞ ; х1 ) U (х2 ; + ∞ )
Бос жиын
Бос жиын (х1 ; х2)
8. Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі
1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c<0) түріне келтіру2. y=ax2+bx+c функциясын қарастырамыз
3. Парабола тармақтарының бағытын анықтау
4. Параболаның ох осін қиятын нүктелерін анықтау
(ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін
көрсетеміз
8. Аралықпен жауабын жазу
9.
а) 2 x 22 x 4 0;2 x 2 x 4;
D ( 1)2 4 2 4 31 0;
2 x 2 x 4 0;
( ; )
б ) x 2 3x 8 0;
x 2 3x 8;
D 32 4 ( 1) ( 8) 23 0;
x 2 3x 8 0;
Заданное неравенство не имеет решений




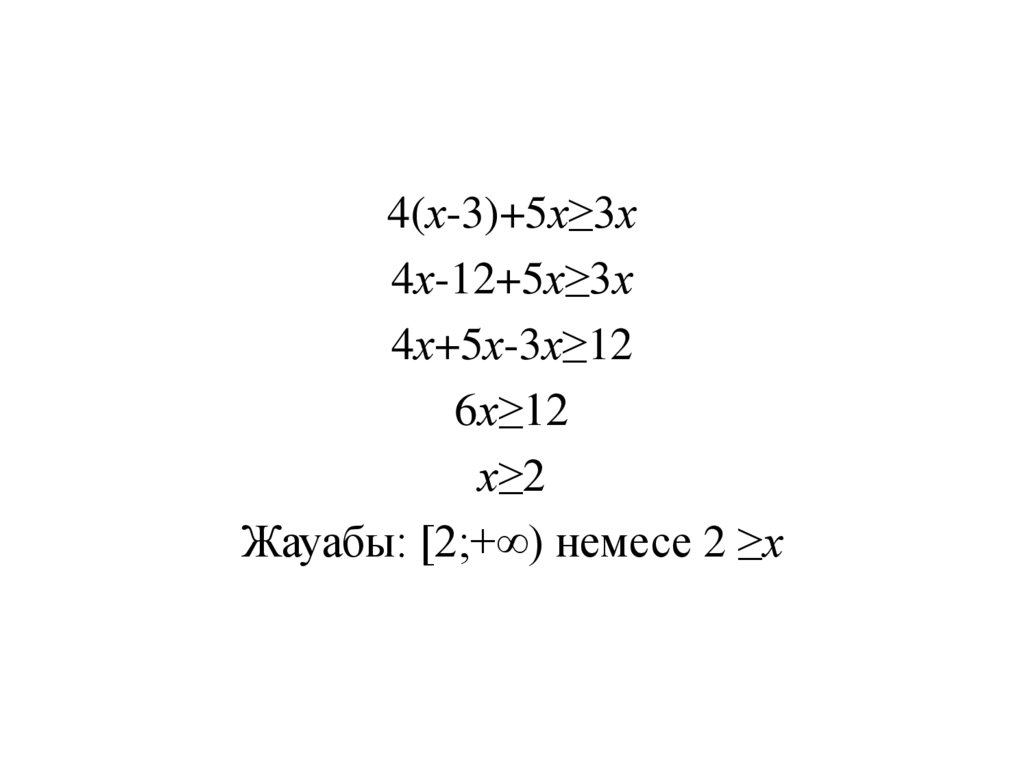




 mathematics
mathematics








