Вычислительная теплофизика. Лекция 1 [2]

1.

Национальный исследовательский ядерный университет «МИФИ»
Вычислительная теплофизика
Меринов Игорь Геннадьевич
Баясхаланов Михаил Валерьевич

Национальный исследовательский ядерный университет «МИФИ»
Задачи курса
Знакомство с методами вычислительной математики,
алгоритмами расчета и принципами их программной
реализации применительно к распространенным
задачам теплообмена

3.

Национальный исследовательский ядерный университет «МИФИ»
Программа курса
1. Реализация на ЭВМ точных аналитических
решений задач теплообмена
2. Численное моделирование процессов
теплопереноса в приближении
сосредоточенных параметров
3. Конечно-разностные методы решения задач
теплопроводности
4. Конечно-разностные методы решения задач
конвективного теплообмена

4.

Национальный исследовательский ядерный университет «МИФИ»
Используемая литература
1. Моделирование теплогидравлических процессов в реакторных установках и
элементах теплообменного оборудования. Лабораторный практикум / Ю.А.
Маслов, И.Г. Меринов, Рябов. М.: МИФИ, 2008.
2. Применение ЭВМ для решения задач теплообмена:
Учеб. Пособие / Г.Н. Дульнев, В.Г. Парфенов, А.В. Сигалов.
М.: Высш. Шк., 1990. – 207 с.
ISBN 5-06-000116-4
3. Численные методы и программное обеспечение: Пер. с англ. /
Д. Каханер, К. Моулер, С. Нэш. М.: Мир, 2001. – 575 с.
ISBN 5-03-003392-0 (рус.)
ISBN 0-13-626672-Х (англ.)

5.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических
решений
Применение:
1. В качестве тестовых для анализа численных решений.
2. Анализ асимптотического поведения решения.
3. Сокращение затрат ресурсов ЭВМ, т.к. рассчитываются
только необходимые значения.
Особенности:
1. Как правило, представляются в виде рядов, интегралов,
часто содержат специальные функции.
2. Часто содержат параметры, являющиеся корнями
трансцендентных уравнений или их систем.

6.

7.

8.

9.

10.

11.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Пример.
Одномерное нестационарное поле температур в неограниченной
пластине с внутренним источником тепловыделения
Таким образом, для проведения расчетов по точному решению (2.13)
необходимо:
1. Найти N значений собственных чисел μn
2. Вычислить интегралы (2.10) для изображений Wn
3. Провести суммирование членов ряда.

12.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений

13.

14.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
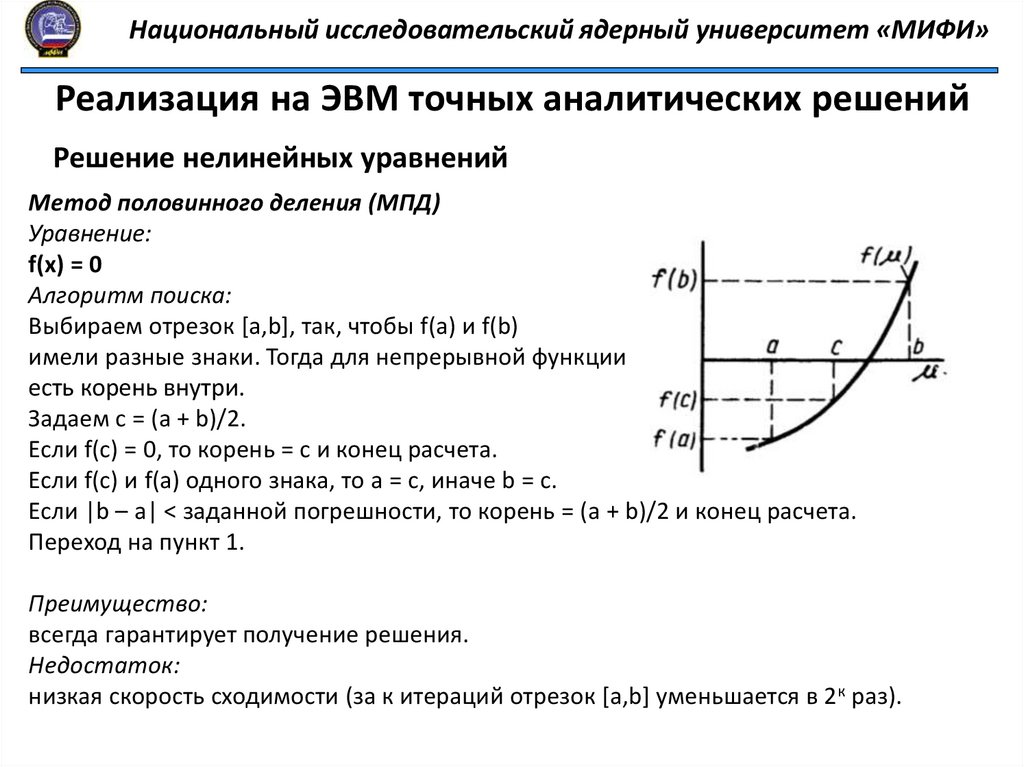
Метод половинного деления (МПД)
Уравнение:
f(x) = 0
Алгоритм поиска:
Выбираем отрезок [a,b], так, чтобы f(a) и f(b)
имели разные знаки. Тогда для непрерывной функции
есть корень внутри.
Задаем c = (a + b)/2.
Если f(c) = 0, то корень = с и конец расчета.
Если f(c) и f(a) одного знака, то а = с, иначе b = c.
Если |b – a| < заданной погрешности, то корень = (a + b)/2 и конец расчета.
Переход на пункт 1.
Преимущество:
всегда гарантирует получение решения.
Недостаток:
низкая скорость сходимости (за к итераций отрезок [a,b] уменьшается в 2к раз).

15.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
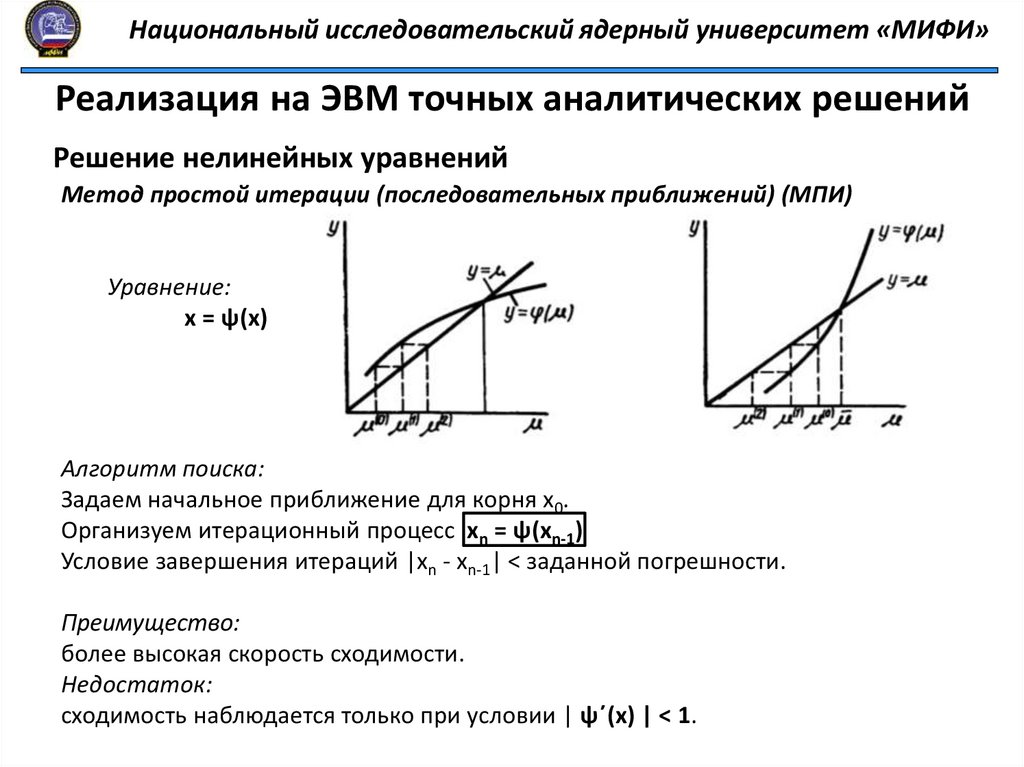
Метод простой итерации (последовательных приближений) (МПИ)
Уравнение:
х = ψ(x)
Алгоритм поиска:
Задаем начальное приближение для корня х0.
Организуем итерационный процесс хn = ψ(xn-1)
Условие завершения итераций |хn - xn-1| < заданной погрешности.
Преимущество:
более высокая скорость сходимости.
Недостаток:
сходимость наблюдается только при условии | ψ΄(x) | < 1.

16.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
Метод простой итерации (последовательных приближений) (МПИ)
Доказательство
xn ψ( xn 1 )
a ψ(a)
( xn a) (ψ( xn 1 ) ψ(a))
xn 1 a
ψ( xn 1 ) ψ(a)
( xn a )
( xn 1 a)
xn 1 a
xn 1 a
ψ '(ξ ), где ξ [xn 1,a]
m max ψ '(ξ )
на отрезке, вкл. все x n .
xn a m x0 a
n
m min ψ '(ξ )
m 1 mn 0
m 1 тогда берем:
на отрезке, вкл. все x n .
x n a m n x 0 a при m 1 m n

17.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
Усовершенствованный метод последовательных приближений
xn 1 xn Δxn , где Δxn ψ( xn ) xn из МПИ.
Возьмем
xn 1 xn αΔxn , где α подгоночныйкоэффициент.
y
tgβ
y=x
(α 1)Δxn (α 1)
ψ '(ξ ), ξ [ xn , a]
αΔxn
α
y=ψ(x)
β
α
45ᴼ
1
1 ψ '(ξ )
Δxn
xn 1 xn α (ψ( xn ) xn )
αΔxn
xn
xn+1 a
x

18.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
Метод Ньютона-Рафсона (МНР)
xn 1 xn α (ψ( xn ) xn ), где α
ψ( xn ) xnψ '( xn )
1
xn 1
g ( xn )
1 ψ '( xn )
1 ψ '( xn )
Метод сходится, если
g '( x ) 1,
g '( x )
ψ ''(x)(ψ(x) x)
1 ψ '(x)
Условия сходимости:
1. х0 близко к решению;
2. Ψ”(x) не слишком велика;
3. Ψ’(x) далека от 1.
Для уравнения F(x) = 0
xn 1 xn
F (x n )
F '( xn )
2

19.

Национальный исследовательский ядерный университет «МИФИ»
Реализация на ЭВМ точных аналитических решений
Решение нелинейных уравнений
Выбор вида уравнения для решения
Решение МПИ
a)
μ Bi ctg μ
б)
μ μ μ
в)
μ μ μ
ψ '( μ ) Bi
sin2 μ
ctg μ ψ '( μ ) 1 1 1 2
Bi
Bi
sin μ
Bi
ctg μ ψ '( μ ) 1 1 1 2
Bi
sin μ
Bi
μn π / 2 πn
б)
Bi 0
μn πn
а)
в ) МПИ расходится при любом Bi

20.

Национальный исследовательский ядерный университет «МИФИ»
Спасибо за внимание !

English Русский Rules