Similar presentations:
Нормальное распределение
1.
Непрерывная случайная величина Хназывается распределенной
по нормальному закону с параметрами
a, σ>0, если она имеет плотность
вероятности
1
f ( x)
2
e
( x a )2
2 2
2.
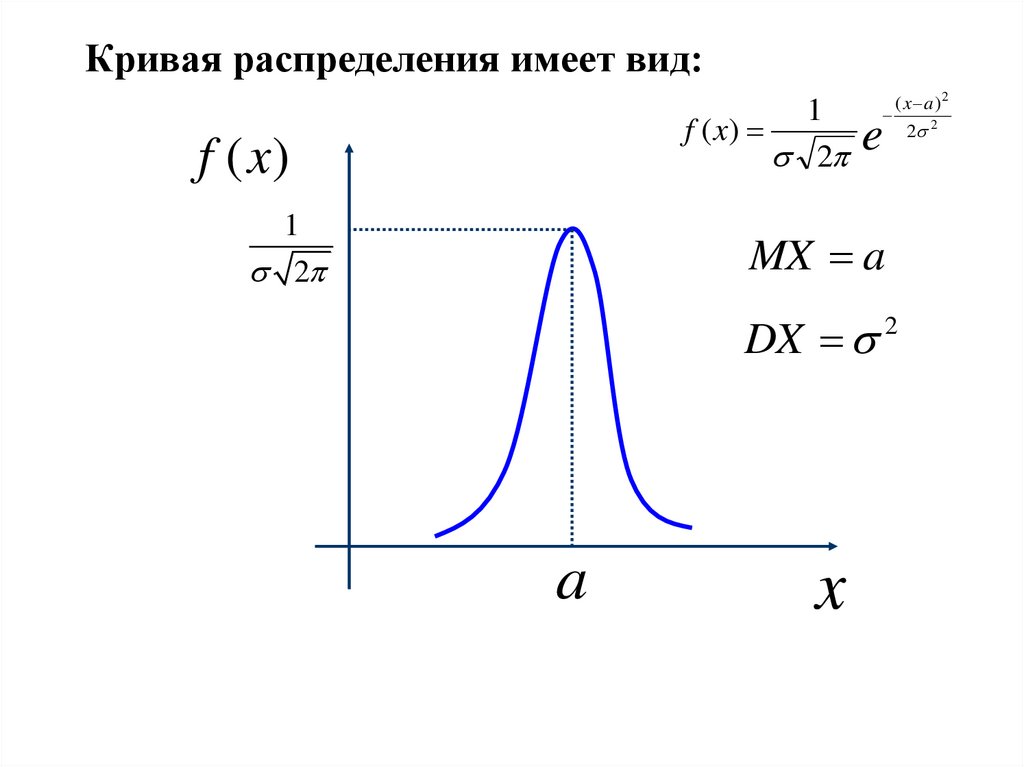
Кривая распределения имеет вид:1
f ( x)
2
f (x)
1
2
( x a )2
e
MX a
DX
a
x
2
2 2
3.
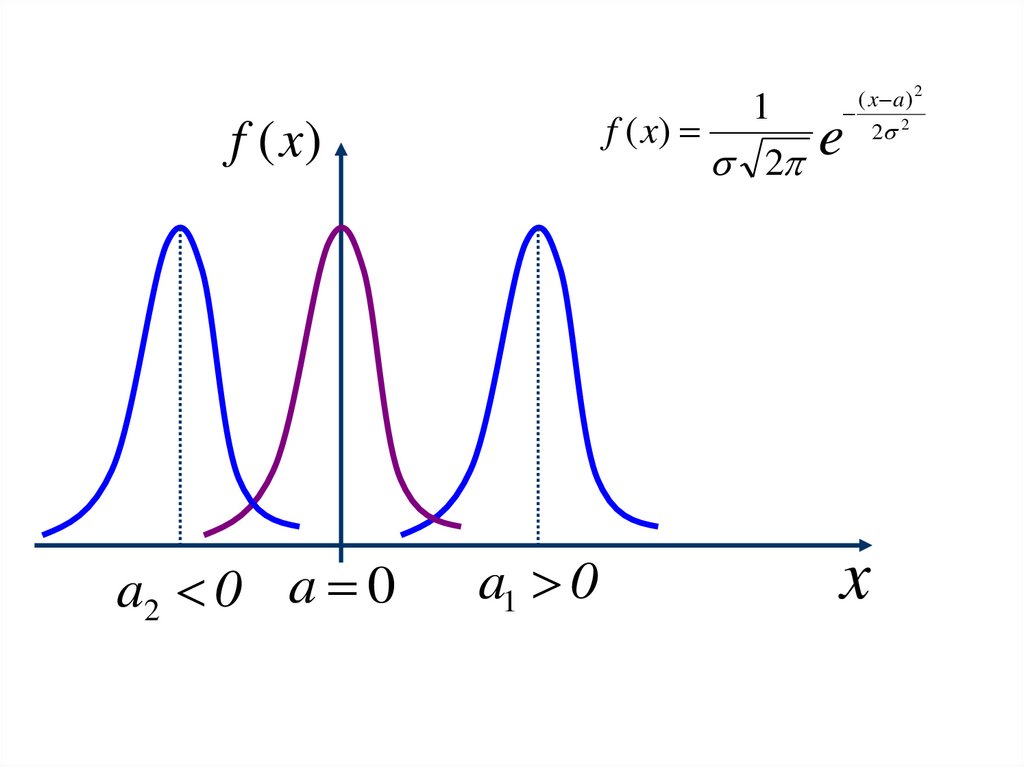
Если изменять параметр a ,кривая распределения будет
смещаться вдоль оси
абсцисс, не изменяя при этом
своей формы.
4.
1f ( x)
2
f (x)
a2 0 a 0
a1 0
( x a )2
e
x
2 2
5.
Параметр σ характеризуетформу
кривой распределения.
При его увеличении кривая
распределения становится более
плоской, и наоборот.
6.
f (x)1
f ( x)
2
e
1
2
3
σ1< σ2< σ3
x
( x a )2
2 2
7.
То, что случайная величина Х распределена понормальному закону с параметрами a, σ>0 ,
обозначается
X N (a, )
MX a
DX
2
8.
X N (a, )P(c X d ) ?
9.
X N (a, )d
d
1
P(c X d ) f ( x)dx
e
c
c 2
( x a )2
2 2
dx
10.
X N (a, )d
d
1
P(c X d ) f ( x)dx
e
c
c 2
( x a )2
2 2
dx
Интеграл аналитически не вычисляется!
11.
1 способ (при вычислении в Excel)P(c x d ) FN ( a , ) d FN ( a , ) c
FN ( a , ) x функция нормального
Распределения, для вычисления
Которой используется функция
НОРМРАСП(x;a;σ;1)
12.
1 способ (при вычислении в Excel)P(c x d ) FN ( a , ) d FN ( a , ) c
НОРМРАСП(x;a;σ;1)
Например, если Х имеет нормальное
распределение со средним a=4 и
среднеквадратичным отклонением σ=2,
то для вычисления P( 1 x 3)
Пишем
НОРМРАСП(3;4;2;1)-НОРМРАСП(-1;4;2;1)
13.
P ( x d ) P ( x d )FN ( a , ) d FN ( a , ) FN ( a , ) d
Например, если Х имеет нормальное
распределение со средним a=4 и
среднеквадратичным отклонением σ=2,
P( x 3)
то для вычисления
Пишем
НОРМРАСП(3;4;2;1)
14.
P( x c) P(c x )FN ( a , ) FN ( a , ) c
1 FN ( a , ) c
15.
P( x c) P(c x )FN ( a , ) FN ( a , ) c
1 FN ( a , ) c
Например, если Х имеет нормальное
распределение со средним a=4 и
среднеквадратичным отклонением σ=2,
то для вычисления P(X>5)
Пишем
1- НОРМРАСП(5;4;2;1)
16.
2 способ (при вычислении вручную)d a
c a
P (c x d ) Ô
Ô
Ф(x) – табличная функция Лапласа
x
Ô ( x)
0
1
2
t2
2
e dt
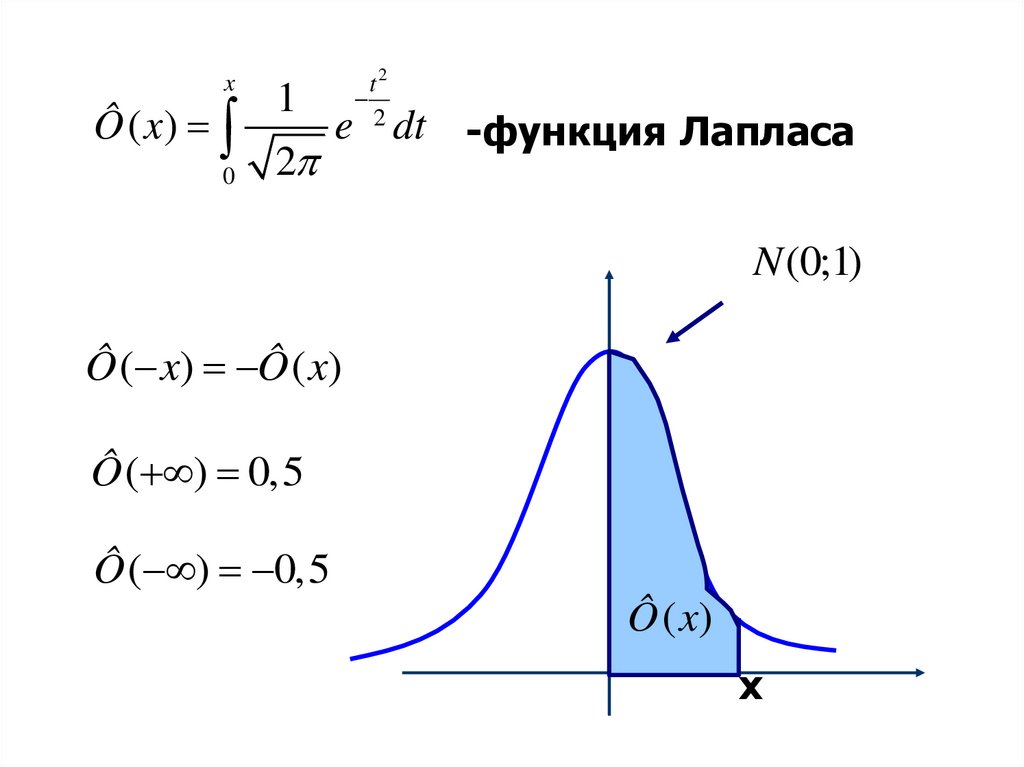
17.
xÔ ( x)
0
1
2
t2
2
e dt -функция Лапласа
N (0;1)
Ô ( x) Ô ( x)
Ô ( ) 0,5
Ô ( ) 0,5
Ô ( x)
х
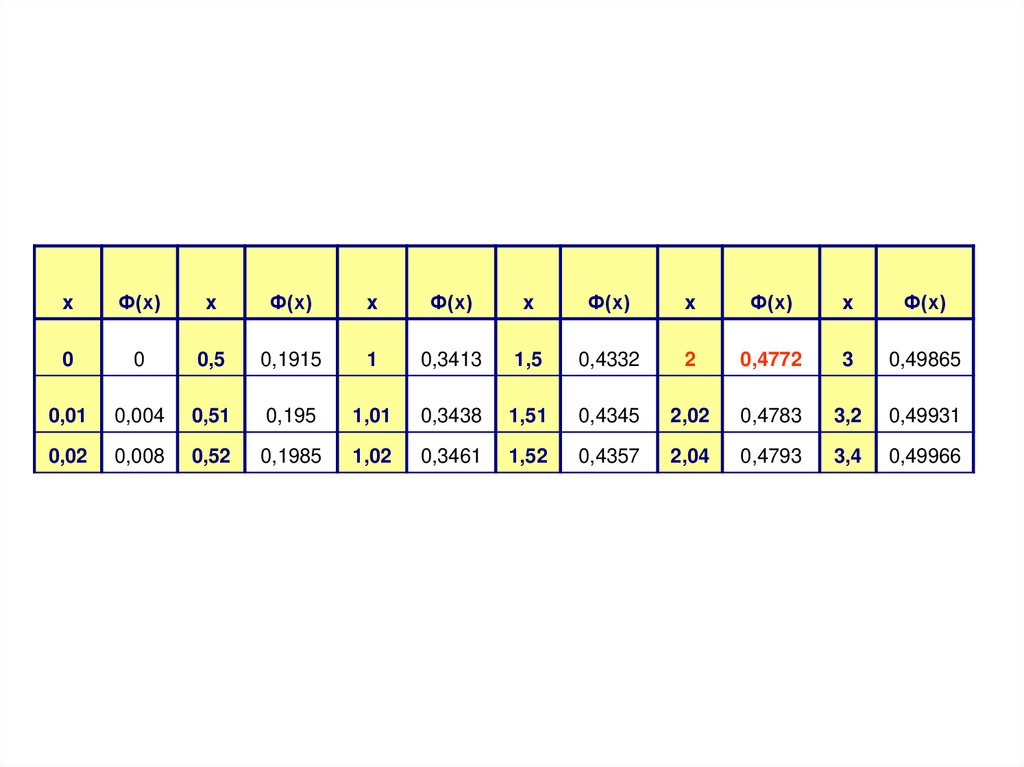
18.
xФ(х)
x
Ф(х)
x
Ф(х)
x
Ф(х)
x
Ф(х)
x
Ф(х)
0
0
0,5
0,1915
1
0,3413
1,5
0,4332
2
0,4772
3
0,49865
0,01
0,004
0,51
0,195
1,01
0,3438
1,51
0,4345
2,02
0,4783
3,2
0,49931
0,02
0,008
0,52
0,1985
1,02
0,3461
1,52
0,4357
2,04
0,4793
3,4
0,49966
19.
P( x d ) P( x d )d a
d a
Ô
Ô Ô
0,5
20.
P ( x c ) P (c x )c a
c a
Ô Ô
0,5 Ô
21.
Пусть случайная величина Х - ростнаугад выбранного студента
подчиняется нормальному
распределению с параметром a=174 см.
и 6 см.
Найти вероятности p(X<190), р(Х>180),
p(160<X<190).
22.
X N (174,6)P( X 190) P( X 190)
В Excel пишем =НОРМРАСП(190;174;6;1)
Вручную
190 174
8
P( X 190)
( ) 0,5
6
3
Ô (2,67) 0,5 0,496 0,5 0,996
Находим в таблице Лапласа
23.
X N (174,6)P( X 180) P(180 X )
В Excel пишем =1-НОРМРАСП(180;174;6;1)
Вручную
180 174
P( X 180) ( )
0,5 (1)
6
0,5 0,34 0,16
24.
X N (174,6)P(160 X 190)
В Excel пишем =НОРМРАСП(190;174;6;1)- НОРМРАСП(160;174;6;1)
Вручную
190 174
160 174
P(160 X 190) Ф
Ф
6
6
8
7
8
7
Ф Ф Ф Ф 0.4963 0.4898 0.986
3
3
3
3
Находим в таблице Лапласа
25.
Пусть Х - нормально распределеннаяслучайная величина с параметрами
a, σ. Тогда
p(a 3 X a 3 ) 1
26.
Действительно,a 3 a a 3 a
P(a 3 X a 3 )
3 3 3 3 0.49865 0.49865 0,9973 1
27.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Изобразить схематично график плотности распределения
•Найти вероятность того, что дневная выручка магазина лежит в интервале
(800;1000).
•Найти вероятность того, что дневная выручка магазина меньше 800 тыс.руб.
•Найти вероятность того, что дневная выручка магазина больше 1000 тыс.руб.
•С помощью правила трех сигм определить, в каком интервале почти наверное (с
вероятностью 0,9973) лежит дневная выручка магазина
28.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Изобразить схематично график плотности распределения
N (900;100)
1
f ( x)
2
f (x)
1
f ( x)
1
100 2
100
e
( x a )2
2 2
e
2
MX 900
2
DX 100
900
x
( x 900)2
2 1002
29.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Найти вероятность того, что дневная выручка магазина лежит в интервале
(800;1000).
•Найти вероятность того, что дневная выручка магазина меньше 800 тыс.руб.
•Найти вероятность того, что дневная выручка магазина больше 1000 тыс.руб.
Решение вручную:
1000 900
800 900
P(800 X 1000) Ф
Ф
100
100
Ф 1 Ф 1 Ф 1 Ф 1 0.341 0.341 0.682
30.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Найти вероятность того, что дневная выручка магазина лежит в интервале
(800;1000).
•Найти вероятность того, что дневная выручка магазина меньше 800 тыс.руб.
•Найти вероятность того, что дневная выручка магазина больше 1000 тыс.руб.
Решение вручную:
800 900
P( X 800) P( X 800) Ф
Ф( )
100
Ф 1 Ф 0.341 0.5 0.159
31.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Найти вероятность того, что дневная выручка магазина лежит в интервале
(800;1000).
•Найти вероятность того, что дневная выручка магазина меньше 800 тыс.руб.
•Найти вероятность того, что дневная выручка магазина больше 1000 тыс.руб.
Решение вручную:
1000 900
P( X 1000) P(1000 X ) Ф( ) Ф
100
0.5 Ф 1 0.5 0.341 0.159
32.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•Найти вероятность того, что дневная выручка магазина лежит в интервале
(800;1000).
•Найти вероятность того, что дневная выручка магазина меньше 800 тыс.руб.
•Найти вероятность того, что дневная выручка магазина больше 1000 тыс.руб.
Решение в Excel:
=НОРМРАСП(1000;900;100;1)НОРМРАСП(800;900;100;1)
=НОРМРАСП(800;900;100;1)
=1-НОРМРАСП(1000;900;100;1)
33.
Дневная выручка магазина является нормально распределенной случайнойвеличиной со средним значением 900 тысяч рублей и среднеквадратичным
отклонением 100 тысяч рублей.
•С помощью правила трех сигм определить, в каком интервале почти наверное (с
вероятностью 0,9973) лежит дневная выручка магазина
X
N (900;100)
p(a 3 X a 3 ) 0.9973
p(900 3 100 X 900 3 100) 0.9973
p(600 X 1200) 0.9973





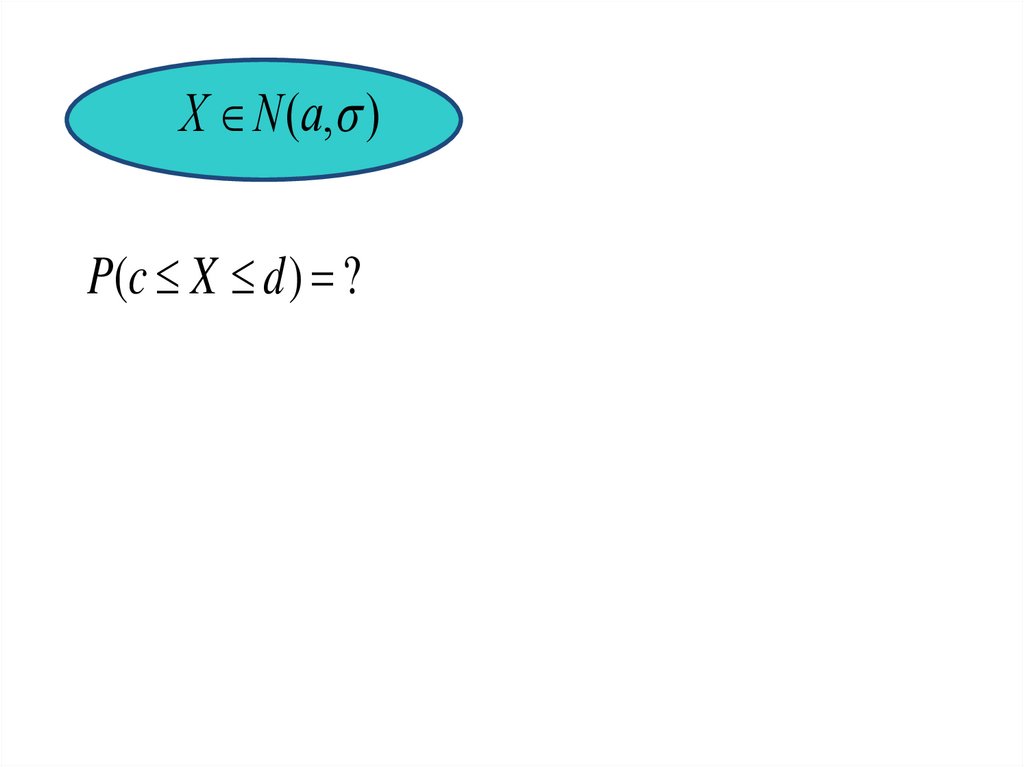
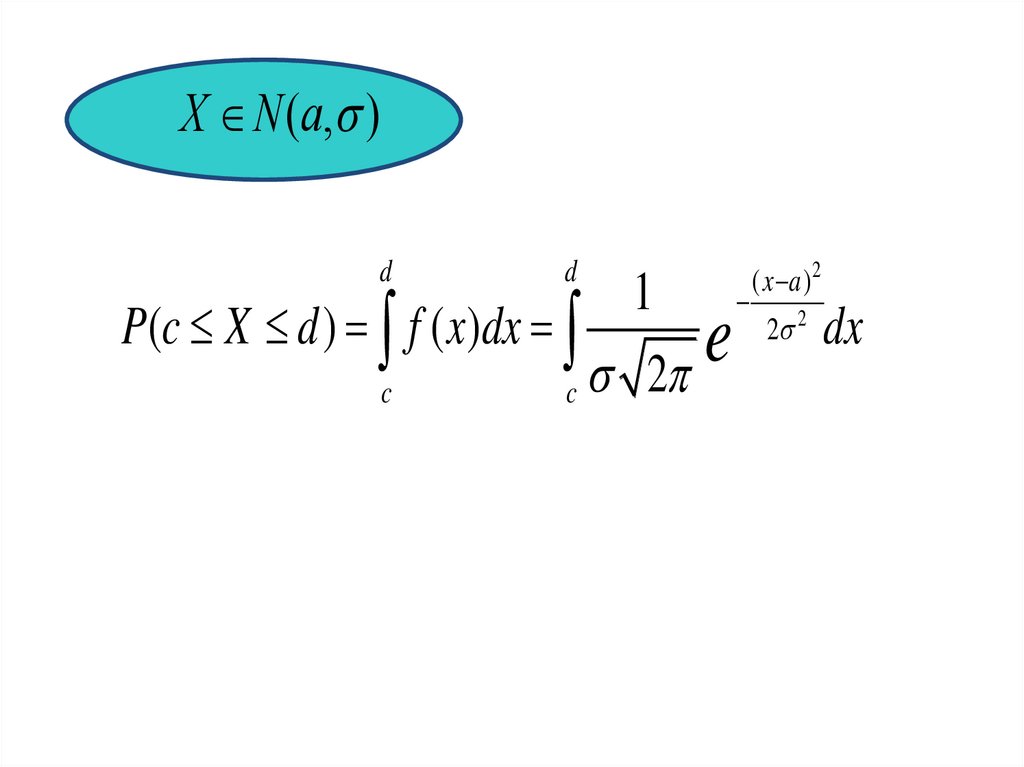




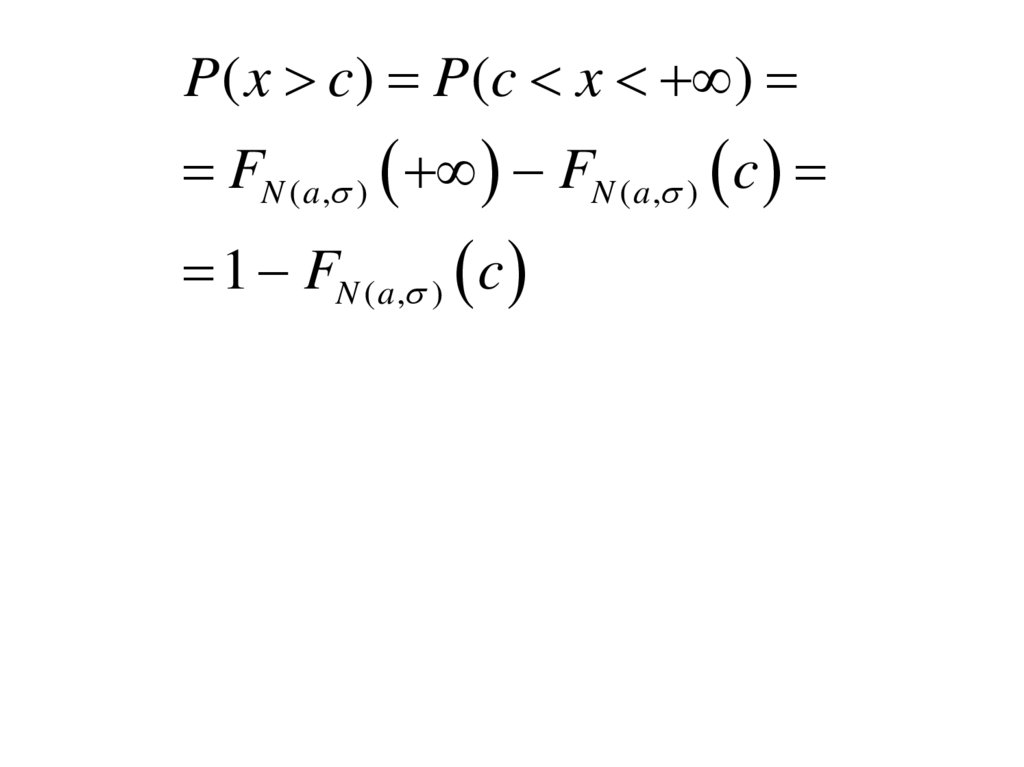



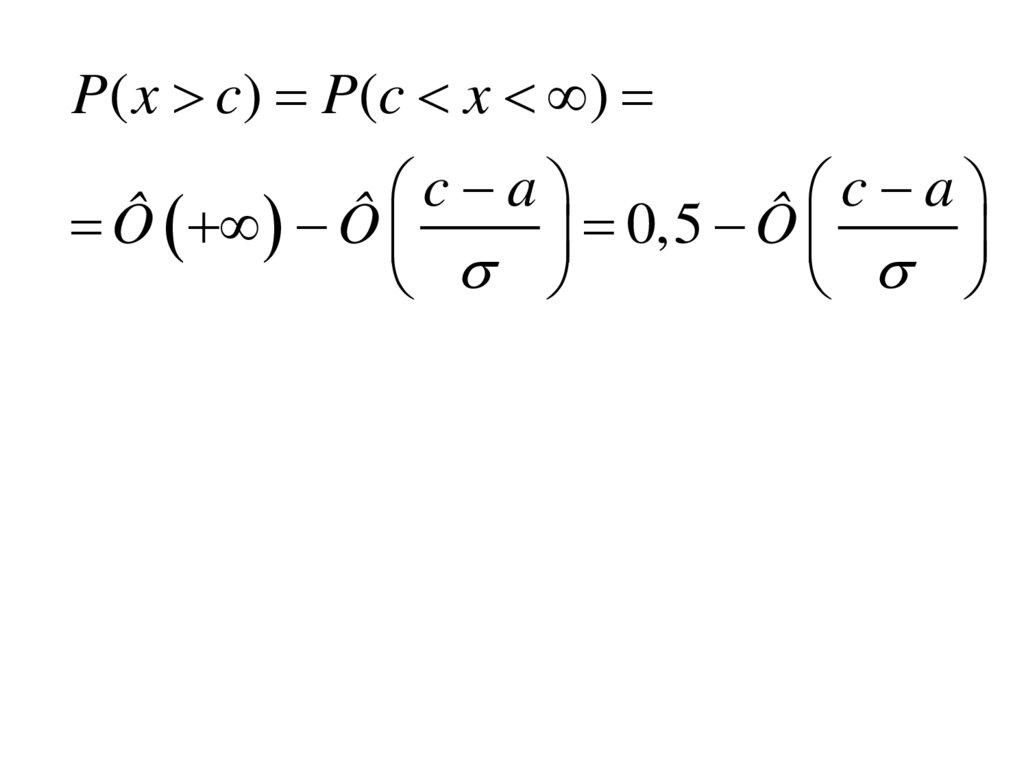













 mathematics
mathematics








